MECÁNICA

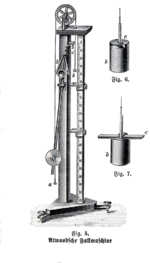
máquina Atwood (o la máquina de Atwood ) fue inventada en 1784 por el matemático inglés George Atwood como un experimento de laboratorio para verificar las leyes mecánicas del movimiento con aceleración constante . La máquina de Atwood es una demostración común en el aula utilizada para ilustrar los principios de la mecánica clásica .

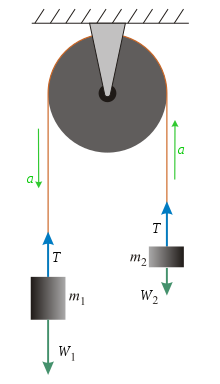
La máquina ideal de Atwood consiste en dos objetos de masa m ₁ y m ₂ , conectados por una cuerda sin masa inextensible sobre una polea sin masa ideal . ^[1]

Cuando m ₁ = m ₂ , la máquina está en equilibrio neutro independientemente de la posición de los pesos.

Cuando m ₁ ≠ m ₂ ambas masas experimentan una aceleración uniforme.

Ilustración de la máquina Atwood, 1905.

Ecuación para aceleración constante [ editar ]

Los diagramas de cuerpo libre de las dos masas colgantes de la máquina Atwood. Nuestra convención de signos , representada por los vectores de aceleración, es que m ₁acelera hacia abajo y que m ₂ acelera hacia arriba, como sería el caso si m ₁> m ₂

Podemos derivar una ecuación para la aceleración analizando las fuerzas. Si consideramos una cuerda sin masa, inextensible y una polea sin masa ideal, las únicas fuerzas que tenemos que considerar son: la fuerza de tensión ( T ) y el peso de las dos masas ( W ₁ y W ₂ ). Para encontrar una aceleración debemos considerar las fuerzas que afectan a cada masa individual. Usando la segunda ley de Newton (con una convención de signos de{\ displaystyle m_ {1}> m_ {2}}) podemos derivar un sistema de ecuaciones para la aceleración ( a ).

Como una convención de signos, asumimos que a es positivo cuando se baja para$${\ displaystyle m_ {1}} y hacia arriba para $${\ displaystyle m_ {2}}. Peso de$${\ displaystyle m_ {1}} y $${\ displaystyle m_ {2}} es simple $${\ displaystyle W_ {1} = m_ {1} g} y $${\ displaystyle W_ {2} = m_ {2} g} respectivamente.

Fuerzas que afectan a m ₁ :

$${\ displaystyle \; m_ {1} gT = m_ {1} a}

Fuerzas que afectan a m ₂ :

$${\ displaystyle \; T-m_ {2} g = m_ {2} a}

Y sumando las dos ecuaciones anteriores obtenemos.

$${\ displaystyle \; m_ {1} g-m_ {2} g = m_ {1} a + m_ {2} a},

y nuestra fórmula concluyente para la aceleración.

$${\ displaystyle a = g {m_ {1} -m_ {2} \ sobre m_ {1} + m_ {2}}}

A la inversa, la aceleración debida a la gravedad, g , se puede encontrar cronometrando el movimiento de los pesos, y calculando un valor para la aceleración uniforme a :$${\ displaystyle a = {\ frac {2d} {t ^ {2}}}}. ^[2]

La máquina Atwood se usa a veces para ilustrar el método lagrangiano de derivar ecuaciones de movimiento. ^[3]

Ecuación para tensión [ editar ]

Puede ser útil conocer una ecuación para la tensión en la cuerda. Para evaluar la tensión, sustituya la ecuación por aceleración en cualquiera de las 2 ecuaciones de fuerza.

$${\ displaystyle a = g {m_ {1} -m_ {2} \ sobre m_ {1} + m_ {2}}}

Por ejemplo, sustituyendo en $${\ displaystyle m_ {1} a = m_ {1} gT}, resulta en

$${\ displaystyle T = {2gm_ {1} m_ {2} \ sobre m_ {1} + m_ {2}} = {2g \ sobre 1 / m_ {1} + 1 / m_ {2}}}

Ecuaciones para una polea con inercia y fricción [ editar ]

Para diferencias de masa muy pequeñas entre m ₁ y m ₂ , la inercia rotacional I de la polea de radio r no se puede descuidar. La aceleración angular de la polea está dada por la condición de no deslizamiento:

$${\ displaystyle \ alpha = {a \ over r},}

dónde $${\ displaystyle \ alpha}Es la aceleración angular. El par neto es entonces:

$${\ displaystyle \ tau _ {\ mathrm {net}} = \ left (T_ {1} -T_ {2} \ right) r- \ tau _ {\ mathrm {friction}} = I \ alpha}

Combinándonos con la segunda ley de Newton para las masas colgantes y resolviendo para T ₁ , T ₂ , y a , obtenemos:

Aceleración:

$${\ displaystyle a = {{g (m_ {1} -m_ {2}) - {\ tau _ {\ mathrm {friction}} \ over r}} \ over {m_ {1} + m_ {2} + { {I} \ sobre {r ^ {2}}}}}}

Tensión en el segmento de cuerda más cercano m ₁ :

$${\ displaystyle T_ {1} = {{m_ {1} g (2m_ {2} + {{I} \ sobre {r ^ {2}}} + {{\ tau _ {\ mathrm {friction}}} \ sobre {rg}})} \ sobre {m_ {1} + m_ {2} + {{I} \ sobre {r ^ {2}}}}}}

Tensión en el segmento de cuerda más cercano a m ₂ :

$${\ displaystyle T_ {2} = {{m_ {2} g (2m_ {1} + {{I} \ sobre {r ^ {2}}} + {{\ tau _ {\ mathrm {friction}}} \ sobre {rg}})} \ sobre {m_ {1} + m_ {2} + {{I} \ sobre {r ^ {2}}}}}}

Si la fricción del rodamiento es despreciable (pero no la inercia de la polea y no la tracción de la cuerda en el borde de la polea), estas ecuaciones se simplifican al obtener los siguientes resultados:

Aceleración:

$${\ displaystyle a = {{g (m_ {1} -m_ {2})} \ sobre {m_ {1} + m_ {2} + {{I} \ sobre {r ^ {2}}}}}}

Tensión en el segmento de cuerda más cercano m ₁ :

$${\ displaystyle T_ {1} = {{m_ {1} g (2m_ {2} + {{I} \ sobre {r ^ {2}}})} \ sobre {m_ {1} + m_ {2} + {{I} \ sobre {r ^ {2}}}}}}

Tensión en el segmento de cuerda más cercano a m ₂ :

$${\ displaystyle T_ {2} = {{m_ {2} g (2m_ {1} + {{I} \ sobre {r ^ {2}}})} \ sobre {m_ {1} + m_ {2} + {{I} \ sobre {r ^ {2}}}}}}

Implementaciones prácticas [ editar ]

Las ilustraciones originales de Atwood muestran el eje de la polea principal apoyado en las llantas de otras cuatro ruedas, para minimizar las fuerzas de fricción de los rodamientos . Muchas implementaciones históricas de la máquina siguen este diseño.

Un elevador con un contrapeso se aproxima a una máquina ideal de Atwood y por lo tanto libera al motor impulsor de la carga de sostener la cabina del elevador; solo tiene que superar la diferencia de peso y la inercia de las dos masas. El mismo principio se usa para los funiculares con dos vagones conectados en vías inclinadas, y para los ascensores en la Torre Eiffel que se compensan entre sí. Los remontes son otro ejemplo, donde las góndolas se mueven en un sistema cerrado (continuo) de poleas arriba y abajo de la montaña. El remonte es similar al elevador de contrapesada, pero con una fuerza de restricción provista por el cable en la dimensión vertical, lo que permite trabajar tanto en la dimensión horizontal como en la vertical. Ascensores para barcos ^[4]son otro tipo de sistema de elevador contrapesado que se aproxima a una máquina Atwood.

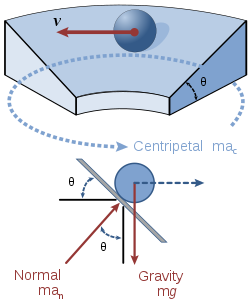
giro acumulado (o giro bancario ) es un giro o cambio de dirección en el que el vehículo se inclina o se inclina, generalmente hacia el interior del giro. Para una carretera o ferrocarril, esto se debe generalmente a que el lecho de la calzada tiene una pendiente descendente transversal hacia el interior de la curva. El ángulo de inclinación es el ángulo al que el vehículo está inclinado sobre su eje longitudinal con respecto a la horizontal.

Encender superficies planas [ editar ]

Si el ángulo de inclinación es cero, la superficie es plana y la fuerza normal es verticalmente hacia arriba. La única fuerza que mantiene al vehículo girando en su trayectoria es la fricción o la tracción . Esto debe ser lo suficientemente grande como para proporcionar la fuerza centrípeta , una relación que se puede expresar como una desigualdad, asumiendo que el automóvil está conduciendo en un círculo de radio r :

{\ displaystyle \ mu mg> {mv ^ {2} \ over r}.}

La expresión en el lado derecho es la aceleración centrípeta multiplicada por la masa, la fuerza requerida para girar el vehículo. El lado izquierdo es la fuerza de fricción máxima, que es igual al coeficiente de fricción μmultiplicado por la fuerza normal. Reorganizar la velocidad máxima de curva es

{\ displaystyle v <{\ sqrt {r \ mu g}}.}

Tenga en cuenta que μ puede ser el coeficiente de fricción estática o dinámica. En este último caso, cuando el vehículo se desliza alrededor de una curva, la fricción está en su límite y las desigualdades se convierten en ecuaciones. Esto también ignora efectos como la fuerza aerodinámica, que puede aumentar la fuerza normal y la velocidad de giro.

Sin fricción a su vez depositado [ editar ]

Panel superior: Bola en una pista circular agrupada que se mueve con velocidad constante v ; Panel inferior: Fuerzas sobre el balón. La fuerza resultante o neta sobre la bola encontrada por la adición vectorial de la fuerza normal ejercida por la carretera y la fuerza vertical debida a la gravedad debe ser igual a la fuerza requerida para la aceleración centrípeta dictada por la necesidad de recorrer una trayectoria circular.

A diferencia de un vehículo que circula a lo largo de un círculo plano, los bordes inclinados agregan una fuerza adicional que mantiene al vehículo en su camino y evita que un automóvil se "arrastre hacia" o "salga" del círculo (o que una rueda del ferrocarril se mueva hacia los lados). para frotar casi la brida de la rueda ). Esta fuerza es el componente horizontal de la fuerza normal del vehículo. En ausencia de fricción, la fuerza normal es la única que actúa sobre el vehículo en la dirección del centro del círculo. Por lo tanto, según la segunda ley de Newton, podemos establecer el componente horizontal de la fuerza normal igual a la masa multiplicada por la aceleración centrípeta: ^[1]

$${\ displaystyle N \ sin \ theta = {mv ^ {2} \ over r}}

Debido a que no hay movimiento en la dirección vertical, la suma de todas las fuerzas verticales que actúan en el sistema debe ser cero. Por lo tanto, podemos establecer el componente vertical de la fuerza normal de los vehículos igual a su peso: ^[1]

$${\ displaystyle N \ cos \ theta = mg}

Resolviendo la ecuación anterior para la fuerza normal y sustituyendo este valor en nuestra ecuación anterior, obtenemos:

$${\ displaystyle {mv ^ {2} \ over r} = {mg \ tan \ theta}}

Esto es equivalente a:

$${\ displaystyle {v ^ {2} \ over r} = {g \ tan \ theta}}

Resolviendo para la velocidad tenemos:

$${\ displaystyle v = {\ sqrt {rg \ tan \ theta}}}

Esto proporciona la velocidad que, en ausencia de fricción y con un ángulo de inclinación y un radio de curvaturadados , asegurará que el vehículo permanezca en su trayectoria designada. La magnitud de esta velocidad también se conoce como la "velocidad nominal" (o "velocidad de equilibrado" para ferrocarriles) de una curva o curva. ^[2] Observe que la velocidad nominal de la curva es la misma para todos los objetos masivos, y una curva que no está inclinada tendrá una velocidad nominal de 0.

Giro bancado con fricción [ editar ]

Al considerar los efectos de la fricción en el sistema, una vez más debemos tener en cuenta en qué dirección apunta la fuerza de fricción. Al calcular una velocidad máxima para nuestro automóvil, la fricción apuntará hacia abajo de la inclinación y hacia el centro del círculo. Por lo tanto, debemos agregar la componente horizontal de fricción a la de la fuerza normal. La suma de estas dos fuerzas es nuestra nueva fuerza neta en la dirección del centro del giro (la fuerza centrípeta):

$${\ displaystyle {mv ^ {2} \ sobre r} = \ mu _ {s} N \ cos \ theta + N \ sin \ theta}

Una vez más, no hay movimiento en la dirección vertical, lo que nos permite establecer todas las fuerzas verticales opuestas iguales entre sí. Estas fuerzas incluyen el componente vertical de la fuerza normal que apunta hacia arriba y tanto el peso del auto como el componente vertical de fricción apuntan hacia abajo:

$${\ displaystyle N \ cos \ theta = \ mu _ {s} N \ sin \ theta + mg}

Al resolver la ecuación anterior para la masa y al sustituir este valor en nuestra ecuación anterior, obtenemos:

$${\ displaystyle {v ^ {2} \ left (N \ cos \ theta - \ mu _ {s} N \ sin \ theta \ right) \ over rg} = \ mu _ {s} N \ cos \ theta + N \ sin \ theta}

Resolviendo para v obtenemos:

$${\ displaystyle v = {\ sqrt {rg \ left (\ sin \ theta + \ mu _ {s} \ cos \ theta \ right) \ over \ cos \ theta - \ mu _ {s} \ sin \ theta}} = {\ sqrt {rg \ left (\ tan \ theta + \ mu _ {s} \ right) \ sobre 1- \ mu _ {s} \ tan \ theta}}}

Esta ecuación proporciona la velocidad máxima para el automóvil con el ángulo de inclinación dado, el coeficiente de fricción estática y el radio de curvatura. Mediante un análisis similar de la velocidad mínima, se representa la siguiente ecuación:

$${\ displaystyle v = {\ sqrt {rg \ left (\ sin \ theta - \ mu _ {s} \ cos \ theta \ right) \ over \ cos \ theta + \ mu _ {s} \ sin \ theta}} = {\ sqrt {rg \ left (\ tan \ theta - \ mu _ {s} \ right) \ over 1+ \ mu _ {s} \ tan \ theta}}}

La diferencia en este último análisis se produce cuando se considera la dirección de fricción para la velocidad mínima del automóvil (hacia el exterior del círculo). En consecuencia, se realizan operaciones opuestas cuando se inserta fricción en las ecuaciones de las fuerzas en las direcciones centrípeta y vertical.

Las curvas de carreteras incorrectamente almacenadas aumentan el riesgo de choques fuera de carretera y de frente. Se puede esperar que una deficiencia de 2% en la peralte (por ejemplo, una peralte de 4% en una curva que debería tener un 6%) aumente la frecuencia de choque en un 6%, y una deficiencia de 5% la aumentará en un 15%. ^[3] Hasta ahora, los ingenieros viales han estado sin herramientas eficientes para identificar curvas incorrectamente almacenadas y para diseñar acciones viales mitigantes relevantes. Un moderno perfilógrafopuede proporcionar datos tanto de la curvatura de la carretera como de la pendiente transversal (ángulo de inclinación). En el proyecto EU Roadex III de la UE se desarrolló una demostración práctica de cómo evaluar los giros mal almacenados. Ver el documento de referencia vinculado a continuación.

A su vez depositado en la aeronáutica [ editar ]

Douglas DC-3 bancario para dar vuelta a la izquierda.

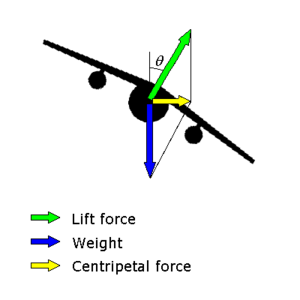
Cuando una aeronave de ala fija está girando (cambiando su dirección), la aeronave debe rodar a una posición de banco para que sus alasformen un ángulo hacia la dirección deseada de la vuelta. Cuando se haya completado el giro, el avión debe volver a la posición de nivel de las alas para reanudar el vuelo recto. ^[4]

Cuando un vehículo en movimiento está girando, es necesario que las fuerzas que actúan sobre el vehículo se sumen a una fuerza interna neta que cause la aceleración centrípeta . En el caso de que una aeronave realice un giro, la fuerza que causa la aceleración centrípeta es el componente horizontal del elevador que actúa sobre la aeronave.

En vuelo recto y nivelado, el ascensor que actúa sobre la aeronave actúa verticalmente hacia arriba para contrarrestar el peso de la aeronave que actúa hacia abajo. Durante un giro equilibrado donde el ángulo de alabeo es θ los actos de elevación en un ángulo theta lejos de la vertical. Es útil para resolver la elevación en un componente vertical y un componente horizontal. Si la aeronave debe continuar en vuelo nivelado (es decir, a una altitud constante ), el componente vertical debe continuar igual al peso de la aeronave y, por lo tanto, el piloto debe retroceder un poco más en el stick. La elevación total (ahora en ángulo) es mayor que el peso de la aeronave, por lo que el componente vertical puede igualar el peso. El componente horizontal está desequilibrado, y por lo tanto es la fuerza neta. haciendo que la aeronave acelere hacia adentro y ejecute el giro.

Diagrama vectorial que muestra la sustentación, el peso y la fuerza centrípeta que actúa sobre una aeronave de ala fija durante un giro acumulado.

Banca excesiva

Porque la aceleración centrípeta es:

$${\ displaystyle a = {v ^ {2} \ over r}}

La segunda ley de Newton en la dirección horizontal se puede expresar matemáticamente como:

$${\ displaystyle L \ sin \ theta = {mv ^ {2} \ over r}}

dónde:

L es el ascensor que actúa sobre la aeronave.

θ es el ángulo de banco del avión

m es la masa de la aeronave

v es la verdadera velocidad del avión

r es el radio de la vuelta

En vuelo recto, la sustentación es igual al peso del avión. Al girar en vuelo, la elevación excede el peso de la aeronave, y es igual al peso de la aeronave ( mg ) dividido por el cosenodel ángulo del banco:

$${\ displaystyle L = {mg \ over {\ cos \ theta}}}

donde g es la intensidad de campo gravitacional.

El radio del turno ahora se puede calcular: ^[5]

$${\ displaystyle r = {v ^ {2} \ sobre {g \ tan \ theta}}}

Esta fórmula muestra que el radio de giro es proporcional al cuadrado de la velocidad real del avión . Con una velocidad del aire más alta, el radio de giro es más grande, y con una velocidad del aire más baja, el radio es más pequeño.

Esta fórmula también muestra que el radio de giro disminuye con el ángulo de inclinación. Con un ángulo de banco más alto, el radio de giro es más pequeño y con un ángulo de banco más alto el radio de giro es mayor.

En un giro acumulado a una altitud constante, el factor de carga es igual a 1 / cosθ. Podemos ver que el factor de carga en vuelo recto y nivelado es 1, dado que cos (0) = 1, y para generar una elevación suficiente para mantener una altitud constante, el factor de carga debe acercarse al infinito cuando el ángulo de inclinación se aproxima a 90 ° y cosθ se aproxima a cero . Esto es físicamente imposible, porque las limitaciones estructurales de la aeronave o la resistencia física de los ocupantes se superarán mucho antes de esa fecha.