MECÁNICA

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Ejemplo de una polea diferencial.

Una polea diferencial , también llamada "polea diferencial Weston", a veces " polipasto de cadena " o coloquialmente "caída de cadena", se utiliza para levantar manualmente objetos muy pesados ​​como los motores de automóviles . Se opera tirando de la sección floja de una cadena continua que se envuelve alrededor de las poleas. El tamaño relativo de dos poleas conectadas determina el peso máximo que se puede levantar con la mano. La carga permanecerá en su lugar (y no bajará por la fuerza de la gravedad ) hasta que se tire de la cadena.

Historia [ editar ]

La polea diferencial fue inventada en 1854 por Thomas Aldridge Weston de King's Norton , Inglaterra. ^[2]

Las poleas fueron fabricadas en colaboración con Richard y George Tangye. Según la autobiografía de Richard Tangye , la polea diferencial de Weston evolucionó a partir del molinete chino , con una cadena sin fin que reemplaza la longitud finita de la cuerda. Afirmó que muchas empresas de ingeniería reconocieron la dificultad de desenganchar eficientemente la cadena de los dientes cuando giraban las poleas, pero su empresa desarrolló una cadena de "inclinación" que resolvió el problema. Comercializada como "Bloques de poleas diferenciales de Weston con guías de patentes", la polea tuvo buenas ventas, es decir, 3000 juegos en 9 meses. Se mostró en 5 tamaños, desde 10 de cien pesos (510 kg) hasta 3 toneladas largas (3,000 kg), en la Exposición Internacional de 1862 en Londres. y recibió una medalla por "aplicación original, utilidad práctica y éxito".

Una ferretería desafió a la Tangyes que la polea había estado en uso durante 30 años antes de la patente de Weston, pero el juez, William Página madera falló a favor de los Tangyes porque el mecanismo de acoplamiento era sustancialmente diferente a la presentada como prueba. ^[3]

The Yale Lock Company adquirió los derechos de patente en 1876. ^[2]

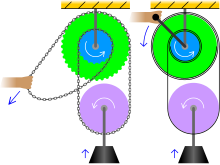
Una polea muda puede levantar masas muy grandes a corta distancia. Consiste en dos poleas fijas de radios desiguales que se unen entre sí y giran juntas, una sola polea que soporta la carga y una cuerda sin fin enrollada alrededor de las poleas. Para evitar el deslizamiento, la cuerda generalmente se reemplaza por una cadena y las poleas conectadas por ruedas dentadas .

Las dos secciones de la cadena que llevan la polea única ejercen pares opuestos y desiguales en las poleas conectadas, de modo que solo la diferencia de estos pares se debe compensar manualmente tirando de la parte suelta de la cadena. Esto lleva a una ventaja mecánica : la fuerza necesaria para levantar una carga es solo una fracción del peso de la carga . Al mismo tiempo, la distancia a la que se levanta la carga es menor que la longitud de la cadena tirada por el mismo factor. Este factor (la ventaja mecánica MA ) depende de la diferencia relativa de los radios r y R de las poleas conectadas:

$${\ displaystyle M \! A = {\ frac {2R} {Rr}} = {\ frac {2} {1 - {\ frac {r} {R}}}}}

El efecto sobre las fuerzas y distancias (ver figura) es cuantitativamente:

$${\ displaystyle F _ {\ mathrm {Z}} = {\ frac {F _ {\ mathrm {L}}} {M \! A}} \ quad, \ quad h = {\ frac {s} {M \! A }} \ quad.}

La diferencia en los radios se puede hacer muy pequeña, lo que hace que la ventaja mecánica de este sistema de poleas sea muy grande. ^[4] [5] En el caso extremo de cero diferencia en los radios, MA se vuelve infinito, por lo que no se necesita fuerza (además de la fricción) para mover la cadena, pero mover la cadena ya no levantará la carga.

En el otro extremo, cuando r es cero, el sistema se convierte en un simple arma con una ventaja mecánica de 2.

Comparación de una polea diferencial (izquierda) y un molinete diferencial o molinete chino (derecha). La cuerda del molinete se representa como espirales para mayor claridad, pero es más probable que sea una hélice con ejes perpendiculares a la imagen.

El mismo principio se usa en un molinete diferencial , donde las poleas conectadas son reemplazadas por tornos .

Cálculo de la ventaja mecánica [ editar ]

En el gráfico anterior, los cuatro segmentos de la cadena están etiquetados como W, X, Y y Z. Las magnitudes de sus fuerzas correspondientes son F _W , F _X , F _Y y F _Z , respectivamente.

Suponiendo que la cadena no tiene masa, F _X = 0 porque el segmento X no soporta ningún peso.

Tomando el sistema en equilibrio, F _W y F _Y son iguales; si no lo fueran, la polea inferior giraría libremente hasta que estuvieran.

A continuación, la fuerza hacia abajo que actúa sobre la polea inferior es igual a la fuerza hacia arriba que actúa sobre ella, por lo que

F _L = F _W + F _Y , o 2 F _W porque F _W = F _Y .

Además, no hay par o momento neto alrededor de la polea compuesta, por lo que el par a la derecha es igual al par a la izquierda:

F _W R + F _X r = F _Y r + F _Z R .

Sustituyendo F _X y F _Y de las ecuaciones anteriores,

F _W R + 0 = F _W r + F _Z R .

Reorganizar da

F _W = F _Z · R/R - r .

Como F _W = F _L/2 ,

F _L/2 =F_Z·R/R - r .

Por último, la ventaja mecánica, F _L/F _Z = 2 R/R - r  o  2/1 - r/R .

La estabilidad direccional es la estabilidad de un cuerpo o vehículo en movimiento alrededor de un eje que es perpendicular a su dirección de movimiento. La estabilidad de un vehículo se relaciona con la tendencia de un vehículo a regresar a su dirección original en relación con el medio que se aproxima (agua, aire, superficie de la carretera, etc.) cuando se lo altera (gira) alejándose de esa dirección original. Si un vehículo es direccionalmente estable, se produce un momento de restauración que está en una dirección opuesta a la perturbación rotacional. Esto "empuja" el vehículo (en rotación) para devolverlo a la orientación original, tendiendo así a mantener el vehículo orientado en la dirección original.

La estabilidad direccional con frecuencia se denomina "desvío del tiempo" porque un vehículo estable en la dirección que gira libremente alrededor de su centro de masa es similar a una veleta que gira alrededor de su pivote (vertical).

Con la excepción de las naves espaciales, los vehículos generalmente tienen una parte delantera y trasera reconocibles y están diseñados para que la parte delantera apunte más o menos en la dirección del movimiento. Sin esta estabilidad, pueden voltearse de extremo a extremo, girar u orientarse a un ángulo de ataque alto , incluso de lado en la dirección del movimiento. En ángulos altos de ataque, las fuerzas de arrastre pueden llegar a ser excesivas, el vehículo puede ser imposible de controlar o incluso puede experimentar una falla estructural. En general, los vehículos terrestres, marítimos, aéreos y submarinos están diseñados para tener una tendencia natural a apuntar en la dirección del movimiento.

Ejemplo: vehículo de carretera [ editar ]

Las flechas, los dardos, los cohetes y las aeronaves tienen superficies de la cola para lograr la estabilidad. Un vehículo de carretera no tiene elementos diseñados específicamente para mantener la estabilidad, pero se basa principalmente en la distribución de masa .

Introducción [ editar ]

Estos puntos se ilustran mejor con un ejemplo. La primera etapa del estudio de la estabilidad de un vehículo de carretera es la derivación de una aproximación razonable a las ecuaciones de movimiento.

El diagrama ilustra un vehículo de cuatro ruedas, en el cual el eje delantero está ubicado a una distancia $${\ displaystyle a}por delante del centro de gravedad y el eje trasero es una distancia$${\ displaystyle b}tras la cg. El cuerpo del coche apunta en una dirección.$${\ displaystyle \ theta} (theta) mientras viaja en una dirección $${\ displaystyle \ psi}(psi). En general, estos no son los mismos. El neumático pisa en la región del punto de contacto en la dirección de desplazamiento, pero los centros están alineados con la carrocería del vehículo, con la dirección en posición central. Los neumáticos se distorsionan a medida que giran para adaptarse a esta desalineación y, como consecuencia, generan fuerzas laterales.

La fuerza lateral neta Y en el vehículo es la fuerza centrípeta que hace que el vehículo cambie la dirección en la que está viajando:

$${\ displaystyle MV {\ frac {d \ psi} {dt}} = Y \, \ cos (\ theta - \ psi)}

donde M es la masa del vehículo y V la velocidad. Todos los ángulos se consideran pequeños, por lo que la ecuación de fuerza lateral es:

$${\ displaystyle MV {\ frac {d \ psi} {dt}} = Y}

La rotación del cuerpo sometido a un momento de guiñada N se rige por:

$${\ displaystyle I {\ frac {d ^ {2} \ theta} {dt ^ {2}}} = N}

Donde está el momento de inercia en la guiñada. Las fuerzas y los momentos de interés surgen de la distorsión de los neumáticos. El ángulo entre la dirección en que rueda la banda de rodadura y el eje se denomina ángulo de deslizamiento . Esto es un poco inapropiado, porque el neumático en su conjunto no se desliza realmente, parte de la región en contacto con la carretera se adhiere, y parte de la región se resbala. Suponemos que la fuerza del neumático es directamente proporcional al ángulo de deslizamiento ($${\ displaystyle \ phi}). Esto se compone del deslizamiento del vehículo como un todo modificado por la velocidad angular del cuerpo. Para el eje delantero:

$${\ displaystyle \ phi (frontal) = \ theta - \ psi - {\ frac {a} {V}} {\ frac {d \ theta} {dt}}}

mientras que para el eje trasero:

$${\ displaystyle \ phi (trasero) = \ theta - \ psi + {\ frac {b} {V}} {\ frac {d \ theta} {dt}}}

Sea la constante de proporcionalidad k. La fuerza lateral es, por lo tanto:

$${\ displaystyle Y = 2k (\ phi (delantero) + \ phi (trasero)) = 4k (\ theta - \ psi) + 2k {\ frac {(ba)} {V}} {\ frac {d \ theta} {dt}}}

El momento es:

$${\ displaystyle N = 2k (a \ phi (delantero) -b \ phi (trasero)) = 2k (ab) (\ theta - \ psi) -2k {\ frac {(a ^ {2} + b ^ {2 })} {V}} {\ frac {d \ theta} {dt}}}

Denotando la velocidad angular $${\ displaystyle \ omega}, las ecuaciones de movimiento son:

$${\ displaystyle {\ frac {d \ omega} {dt}} = 2k {\ frac {(ab)} {I}} (\ theta - \ psi) -2k {\ frac {(a ^ {2} + b ^ {2})} {VI}} \ omega}

$${\ displaystyle {\ frac {d \ theta} {dt}} = \ omega}

$${\ displaystyle {\ frac {d \ psi} {dt}} = {\ frac {4k} {MV}} (\ theta - \ psi) + 2k {\ frac {(ba)} {MV ^ {2}} } \ omega}

Dejar $${\ displaystyle \ theta - \ psi = \ beta} (beta), el ángulo de deslizamiento para el vehículo en su conjunto:

$${\ displaystyle {\ frac {d \ omega} {dt}} = 2k {\ frac {(ab)} {I}} \ beta -2k {\ frac {(a ^ {2} + b ^ {2}) } {VI}} \ omega}

$${\ displaystyle {\ frac {d \ beta} {dt}} = - {\ frac {4k} {MV}} \ beta + (1-2k) {\ frac {(ba)} {MV ^ {2}} } \ omega}

Eliminando $${\ displaystyle \ omega} produce la siguiente ecuación en $${\ displaystyle \ beta}:

$${\ displaystyle {\ frac {d ^ {2} \ beta} {dt ^ {2}}} + ({\ frac {4k} {MV}} + {\ frac {2k (a ^ {2} + b ^ {2})} {VI}}) {\ frac {d \ beta} {dt}} + ({\ frac {4k ^ {2} (a + b) ^ {2}} {MV ^ {2} I }} + {\ frac {2k (ba)} {I}}) \ beta = 0}

Esto se denomina ecuación homogénea lineal de segundo orden, y sus propiedades forman la base de gran parte de la teoría de control .

Análisis de estabilidad [ editar ]

No necesitamos resolver la ecuación de movimiento explícitamente para decidir si la solución diverge indefinidamente o converge a cero después de una perturbación inicial. La forma de la solución depende de los signos de los coeficientes.

El coeficiente de $${\ displaystyle {\ frac {d \ beta} {dt}}}se llamará " amortiguamiento " por analogía con un amortiguador de masa-resorte que tiene una ecuación de movimiento similar.

Por la misma analogía, el coeficiente de $${\ displaystyle \ beta} se llamará 'rigidez', ya que su función es devolver el sistema a cero deflexión, de la misma manera que un resorte.

La forma de la solución depende solo de los signos de los términos de amortiguación y rigidez. Los cuatro tipos de soluciones posibles se presentan en la figura.

La única solución satisfactoria requiere que tanto la rigidez como la amortiguación sean positivas.

El término de amortiguación es:

$${\ displaystyle ({\ frac {4k} {MV}} + {\ frac {2k (a ^ {2} + b ^ {2})} {VI}})}

El coeficiente de deslizamiento del neumático k es positivo, al igual que la masa, el momento de inercia y la velocidad, por lo que la amortiguación es positiva y el movimiento direccional debe ser dinámicamente estable.

El término rigidez es:

$${\ displaystyle ({\ frac {4k ^ {2} (a + b) ^ {2}} {MIV ^ {2}}} + {\ frac {2k (ba)} {I}})}

Si el centro de gravedad está delante del centro de la distancia entre ejes ({\ displaystyle (b> a)}Esto siempre será positivo y el vehículo estará estable a todas las velocidades. Sin embargo, si está más lejos en la popa, el término tiene el potencial de volverse negativo por encima de una velocidad dada por:

$${\ displaystyle V ^ {2} = {\ frac {2k (a + b) ^ {2}} {M (ab)}}}

Por encima de esta velocidad, el vehículo será direccionalmente inestable .

Efecto relativo de los neumáticos delanteros y traseros [ editar ]

Si por alguna razón (presión de inflado incorrecta, huella desgastada) los neumáticos en un eje son incapaces de generar una fuerza lateral significativa, la estabilidad obviamente se verá afectada.

Supongamos, para empezar, que los neumáticos traseros están defectuosos, ¿cuál es el efecto sobre la estabilidad? Si los neumáticos traseros no producen fuerzas significativas, la fuerza lateral y el momento de guiñada se convierten en:

$${\ displaystyle Y = 2k (\ phi (frente)) = 2k (\ theta - \ psi) -2k {\ frac {a} {V}} {\ frac {d \ theta} {dt}}}

$${\ displaystyle N = 2k (a \ phi (frente)) = 2ka (\ theta - \ psi) -2k {\ frac {a ^ {2}} {V}} {\ frac {d \ theta} {dt} }}

La ecuación de movimiento se convierte en:

$${\ displaystyle {\ frac {d ^ {2} \ beta} {dt ^ {2}}} + ({\ frac {2k} {MV}} + {\ frac {2ka ^ {2}} {VI}} ) {\ frac {d \ beta} {dt}} - ({\ frac {2ka} {I}}) \ beta = 0}

El coeficiente de $${\ displaystyle \ beta} es negativo, por lo que el vehículo será inestable.

Ahora considere el efecto de los neumáticos defectuosos en la parte delantera. La fuerza lateral y el momento de guiñada se convierten en:

$${\ displaystyle Y = 2k (\ phi (trasero)) = 2k (\ theta - \ psi) + 2k {\ frac {b} {V}} {\ frac {d \ theta} {dt}}}

$${\ displaystyle N = -2k (b \ phi (trasero)) = - 2kb (\ theta - \ psi) -2k {\ frac {b ^ {2}} {V}} {\ frac {d \ theta} { dt}}}

La ecuación de movimiento se convierte en:

$${\ displaystyle {\ frac {d ^ {2} \ beta} {dt ^ {2}}} + ({\ frac {2k} {MV}} + {\ frac {2kb ^ {2}} {VI}} ) {\ frac {d \ beta} {dt}} + ({\ frac {2kb} {I}}) \ beta = 0}

El coeficiente de $${\ displaystyle \ beta} es positivo, por lo que el vehículo será estable pero no soportable.

De ello se deduce que el estado de los neumáticos traseros es más crítico para la estabilidad direccional que el estado de los neumáticos delanteros. Además, al bloquear las ruedas traseras aplicando el freno de mano, el vehículo se vuelve inestable direccionalmente, lo que hace que gire. Dado que el vehículo no está bajo control durante el giro, el " giro del freno de mano " generalmente es ilegal en las vías públicas.

Fuerzas de dirección [ editar ]

La desviación de la dirección cambia el ángulo de deslizamiento de los neumáticos delanteros, generando una fuerza lateral. Con la dirección convencional, los neumáticos se desvían en diferentes cantidades, pero a los efectos de este análisis, el deslizamiento adicional se considerará igual para ambos neumáticos delanteros.

La fuerza lateral se convierte en:

$${\ displaystyle Y = 2k (\ phi (delantero) + \ phi (trasero)) = 4k (\ theta - \ psi) + 2k {\ frac {(ba)} {V}} {\ frac {d \ theta} {dt}} + 2k \ eta}

dónde $${\ displaystyle \ eta}(eta) es la desviación de la dirección. Del mismo modo, el momento de guiñada se convierte en:

$${\ displaystyle N = 2k (a \ phi (delantero) -b \ phi (trasero)) = 2k (ab) (\ theta - \ psi) -2k {\ frac {(a ^ {2} + b ^ {2 })} {V}} {\ frac {d \ theta} {dt}} + 2ka \ eta}

Incluir el término directivo introduce una respuesta forzada:

$${\ displaystyle {\ frac {d ^ {2} \ beta} {dt ^ {2}}} + ({\ frac {4k} {MV}} + {\ frac {2k (a ^ {2} + b ^ {2})} {VI}}) {\ frac {d \ beta} {dt}} + ({\ frac {4k ^ {2} (a + b) ^ {2}} {MV ^ {2} I }} + {\ frac {2k (ba)} {I}}) \ beta = - {\ frac {2k} {MV}} {\ frac {d \ eta} {dt}} + ({\ frac {2ka } {I}} - {\ frac {4k ^ {2} b (a + b)} {IMV ^ {2}}}) \ eta}

La respuesta de estado estable es con todas las derivadas de tiempo establecidas en cero. La estabilidad requiere que el coeficiente de$${\ displaystyle \ beta} debe ser positivo, por lo que el signo de la respuesta está determinado por el coeficiente de $${\ displaystyle \ eta}:

$${\ displaystyle ({\ frac {2ka} {I}} - {\ frac {4k ^ {2} b (a + b)} {IMV ^ {2}}})}

Esta es una función de la velocidad. Cuando la velocidad es baja, el deslizamiento es negativo y el cuerpo apunta fuera de la esquina ( subvirte ). A una velocidad dada por:

$${\ displaystyle V ^ {2} = {\ frac {2kb (a + b)} {Ma}}}

El cuerpo apunta en la dirección del movimiento. Por encima de esta velocidad, el cuerpo apunta hacia la esquina ( sobrevirajes ).

Como ejemplo:

con k = 10kN / radián, M = 1000kg, b = 1.0m, a = 1.0m, los vehículos subvierten por debajo de 11.3 mph.

Evidentemente, mover el centro de gravedad hacia adelante aumenta esta velocidad, lo que le da al vehículo una tendencia a subvirar .

Nota: la instalación de un motor pesado y pesado en un vehículo de producción de peso ligero diseñado alrededor de un motor pequeño aumenta tanto su estabilidad direccional como su tendencia a subvirar. El resultado es un vehículo sobrecargado con un rendimiento deficiente en las curvas.

Aún peor es la instalación de una unidad de potencia de gran tamaño en un vehículo de producción con motor trasero sin la correspondiente modificación de la suspensión o distribución de masa, ya que el resultado será direccionalmente inestable a alta velocidad.

Limitaciones del análisis [ editar ]

Las fuerzas derivadas del deslizamiento dependen de la carga en el neumático y del ángulo de deslizamiento; este efecto se ha ignorado, pero se puede tener en cuenta al asumir diferentes valores de k para los ejes delantero y trasero. El movimiento de balanceo debido a las curvas redistribuirá las cargas de los neumáticos entre el lado cercano y el lado exterior del vehículo, modificando nuevamente las fuerzas del neumático. El par motor también redistribuye la carga entre los neumáticos delanteros y traseros.

Un análisis completo también debe tener en cuenta la respuesta de la suspensión .

El análisis completo es esencial para el diseño de vehículos de carretera de alto rendimiento, pero está fuera del alcance de este artículo.