MECÁNICA

la respuesta a la colisión se ocupa de los modelos y algoritmos para simular los cambios en el movimiento de dos cuerpos sólidos después de la colisión y otras formas de contacto.

Contacto de cuerpo rígido [ editar ]

Las fases de compresión y expansión de una colisión entre dos cuerpos sólidos.

Dos cuerpos rígidosen movimiento no restringido, potencialmente bajo la acción de fuerzas, pueden modelarse resolviendo sus ecuaciones de movimiento usando técnicas de integración numérica . En caso de colisión, las propiedades cinéticas de dos de estos cuerpos parecen sufrir un cambio instantáneo, lo que generalmente hace que los cuerpos reboten entre sí, se deslicen o se establezcan en contacto estático relativo, dependiendo de la elasticidad de los materiales y la configuración de la colisión. .

Fuerzas de contacto [ editar ]

El origen del fenómeno de rebote, o reacción , puede atribuirse al comportamiento de cuerpos reales que, a diferencia de sus homólogos idealizados perfectamente rígidos, sufren una compresión menor en la colisión, seguida de expansión, antes de la separación. La fase de compresión convierte la energía cinética de los cuerpos en energía potencial y, en cierta medida, en calor. La fase de expansión convierte la energía potencial de nuevo en energía cinética.

Durante las fases de compresión y expansión de dos cuerpos en colisión, cada cuerpo genera fuerzas reactivas en el otro en los puntos de contacto, de modo que las fuerzas de reacción de la suma de un cuerpo son iguales en magnitud pero opuestas en dirección a las fuerzas del otro, como Por el principio newtoniano de acción y reacción. Si se ignoran los efectos de la fricción, se considera que una colisión afecta solo a la componente de las velocidades que se dirigen a lo largo del contacto normal y que no afecta a las componentes tangenciales.

Reaccion [ editar ]

El grado de energía cinética relativa retenida después de una colisión, denominada restitución , depende de la elasticidad de los materiales de los cuerpos. El coeficiente de restitución entre dos materiales dados se modela como la relación$${\ displaystyle e \ en [0..1]}de la velocidad relativa posterior a la colisión de un punto de contacto a lo largo del contacto normal, con respecto a la velocidad relativa previa a la colisión del mismo punto a lo largo de la misma normalidad. Estos coeficientes generalmente se determinan empíricamente para diferentes pares de materiales, como madera contra hormigón o caucho contra madera. Valores para$${\ displaystyle e}cerca de cero indican colisiones inelásticas, como un trozo de arcilla blanda que golpea el piso, mientras que los valores cercanos a uno representan colisiones altamente elásticas, como una pelota de goma que rebota en una pared. La pérdida de energía cinética es relativa a un cuerpo con respecto al otro. Por lo tanto, el impulso total de ambos cuerpos con respecto a alguna referencia común permanece sin cambios después de la colisión, en línea con el principio de conservación del impulso .

Fricción [ editar ]

Fricción por imperfecciones de la microestructura superficial.

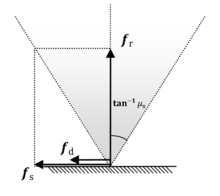
Otro fenómeno de contacto importante es la fricción de superficie a superficie, una fuerza que impide el movimiento relativo de dos superficies en contacto, o la de un cuerpo en un fluido. En esta sección discutimos la fricción de superficie a superficie de dos cuerpos en contacto estático relativo o contacto deslizante. En el mundo real, la fricción se debe a la microestructura imperfecta de las superficies cuyas protuberancias se entrelazan entre sí, generando fuerzas reactivas tangenciales a las superficies.

Para superar la fricción entre dos cuerpos en contacto estático, las superficies deben de alguna manera levantarse una de la otra. Una vez en movimiento, el grado de afinidad de la superficie se reduce y, por lo tanto, los cuerpos en movimiento deslizante tienden a ofrecer una menor resistencia al movimiento. Estas dos categorías de fricción se denominan respectivamente fricción estática y fricción dinámica .

Fuerza aplicada [ editar ]

Es una Fuerza que se aplica a un objeto por otro objeto o por una persona. La dirección de la fuerza aplicada depende de cómo se aplica la fuerza.

Fuerza normal [ editar ]

Es la fuerza de apoyo ejercida sobre un objeto que está en contacto con otro objeto estable. La fuerza normal a veces se denomina fuerza de presión, ya que su acción presiona la superficie en conjunto. La fuerza normal siempre se dirige hacia el objeto y actúa perpendicularmente con la fuerza aplicada.

Fuerza de fricción [ editar ]

Es la fuerza ejercida por una superficie cuando un objeto se mueve a través de ella o hace un esfuerzo para moverse a través de ella. La fuerza de fricción se opone al movimiento del objeto. La fricción se produce cuando dos superficies se presionan juntas, causando atractivas fuerzas intermoleculares entre las moléculas de las dos superficies diferentes. Como tal, la fricción depende de la naturaleza de las dos superficies y del grado en que se presionan entre sí. La fricción siempre actúa paralela a la superficie en contacto y opuesta a la dirección del movimiento. La fuerza de fricción se puede calcular utilizando la ecuación.

Modelo de contacto basado en Impulse [ editar ]

Una fuerza $${\ displaystyle \ mathbf {f} (t) \ in \ mathbb {R} ^ {3}}dependiente del tiempo $${\ displaystyle t \ in \ mathbb {R}}, actuando sobre un cuerpo de masa constante supuesta. $${\ displaystyle m \ in \ mathbb {R}} por un intervalo de tiempo $${\ displaystyle \ lbrack t_ {0} .. t_ {1} \ rbrack} Genera un cambio en el impulso del cuerpo. $${\ displaystyle \ mathbf {p} (t) = m \ mathbf {v} (t)}, dónde $${\ displaystyle \ mathbf {v} (t)}Es el cambio resultante en la velocidad. El cambio en el impulso, denominado impulso y denotado por$${\ displaystyle j \ in \ mathbb {R} ^ {3}} así se calcula como

$${\ displaystyle \ mathbf {j} = \ int _ {t_ {0}} ^ {t_ {1}} \ mathbf {f} dt}

Por impulso fijo $${\ displaystyle \ mathbf {j}}, la ecuación sugiere que $${\ displaystyle t_ {1} \ rightarrow t_ {0} \ Rightarrow \ left | \ mathbf {f} \ right | \ rightarrow \ infty}, es decir, un intervalo de tiempo más pequeño debe ser compensado por una fuerza de reacción más fuerte para lograr el mismo impulso. Al modelar una colisión entre cuerpos rígidos idealizados, no es práctico simular las fases de compresión y expansión de la geometría del cuerpo durante el intervalo de tiempo de colisión. Sin embargo, al asumir que una fuerza$${\ displaystyle \ mathbf {f}} se puede encontrar que es igual a $${\ displaystyle 0} en todas partes excepto en $${\ displaystyle t_ {0}}, y tal que el límite

$${\ displaystyle \ lim _ {t_ {1} \ rightarrow t_ {0}} \ int _ {t_ {0}} ^ {t_ {1}} \ mathbf {f} dt}

existe y es igual a $${\ displaystyle \ mathbf {j}}, la noción de impulsos instantáneos se puede introducir para simular un cambio instantáneo en la velocidad después de una colisión.

Modelo de reacción a base de Impulse [ editar ]

La aplicación de los impulsos en el punto de colisión.

El efecto de la fuerza de reacción. $${\ displaystyle \ mathbf {f} _ {r} (t) \ in \ mathbb {R} ^ {3}} durante el intervalo de colisión $${\ displaystyle [t_ {0} .. t_ {1}]} Por lo tanto, puede ser representado por un impulso de reacción instantánea $${\ displaystyle \ mathbf {j} _ {r} (t) \ in \ mathbb {R} ^ {3}}, computado como

$${\ displaystyle \ mathbf {j} _ {r} = \ int _ {t_ {0}} ^ {t_ {1}} \ mathbf {f} _ {r} dt}

Por deducción del principio de acción y reacción, si el impulso de colisión aplicado por el primer cuerpo en el segundo cuerpo en un punto de contacto $${\ displaystyle \ mathbf {p} _ {r} \ in \ mathbb {R} ^ {3}} es $${\ displaystyle \ mathbf {j} _ {r}}, el contra impulso aplicado por el segundo cuerpo en el primero es $${\ displaystyle - \ mathbf {j} _ {r}}. La descomposicion$${\ displaystyle \ pm \ mathbf {j} _ {r} = \ pm j_ {r} \ mathbf {\ hat {n}}} en la magnitud del impulso $${\ displaystyle j_ {r} \ in \ mathbb {R}} y dirección a lo largo del contacto normal. $${\ displaystyle \ mathbf {\ hat {n}}} y su negacion $${\ displaystyle - \ mathbf {\ hat {n}}}permite la derivación de una fórmula para calcular el cambio en las velocidades lineales y angulares de los cuerpos resultantes de los impulsos de colisión. En las siguientes fórmulas,$${\ displaystyle \ mathbf {\ hat {n}}} Siempre se asume que apunta lejos del cuerpo 1 y hacia el cuerpo 2 en el punto de contacto.

Suponiendo la magnitud del impulso de colisión. $${\ displaystyle \ mathbf {j} _ {r}}Se da y, mediante las leyes de movimiento de Newton, la relación entre las velocidades pre y postlineales de los cuerpos es la siguiente:

	$${\ displaystyle \ mathbf {v '} _ {1} = \ mathbf {v} _ {1} - {\ frac {j_ {r}} {m_ {1}}} \ mathbf {\ hat {n}}}	(1a)
	$${\ displaystyle \ mathbf {v '} _ {2} = \ mathbf {v} _ {2} + {\ frac {j_ {r}} {m_ {2}}} \ mathbf {\ hat {n}}}	(1b)

donde, para el $${\ displaystyle i}cuerpo $${\ displaystyle \ mathbf {v} _ {i} \ in \ mathbb {R} ^ {3}} es la velocidad lineal precolisión, $${\ displaystyle \ mathbf {v '} _ {i} \ in \ mathbb {R} ^ {3}} Es la velocidad lineal posterior a la colisión.

Del mismo modo para las velocidades angulares.

	$${\ displaystyle \ mathbf {\ omega '} _ {1} = \ mathbf {\ omega} _ {1} -j_ {r} \ mathbf {I} _ {1} ^ {- 1} (\ mathbf {r} _ {1} \ times \ mathbf {\ hat {n}})}	(2a)
	$${\ displaystyle \ mathbf {\ omega '} _ {2} = \ mathbf {\ omega} _ {2} + j_ {r} \ mathbf {I} _ {2} ^ {- 1} (\ mathbf {r} _ {2} \ times \ mathbf {\ hat {n}})}	(2b)

donde, para el $${\ displaystyle i}cuerpo $${\ displaystyle {\ omega} _ {i} \ in \ mathbb {R} ^ {3}} es la velocidad de precolisión angular, $${\ displaystyle {\ omega '} _ {i} \ in \ mathbb {R} ^ {3}} es la velocidad angular posterior a la colisión, $${\ displaystyle \ mathbf {I} _ {i} \ in \ mathbb {R} ^ {3 \ times 3}}es el tensor de inercia en el marco de referencia mundial, y$${\ displaystyle \ mathbf {r} _ {i} \ in \ mathbb {R} ^ {3}} es offset del punto de contacto compartido $${\ displaystyle \ mathbf {p}} desde el centro de masa.

Las velocidades $${\ displaystyle v_ {p1}, v_ {p2} \ in \ mathbb {R} ^ {3}} de los cuerpos en el punto de contacto se pueden calcular en términos de las respectivas velocidades lineales y angulares, usando

$${\ displaystyle \ mathbf {v} _ {pi} = \ mathbf {v} _ {i} + \ mathbf {\ omega} _ {i} \ times \ mathbf {r} _ {i}}

(3)

para $${\ displaystyle i = 1,2}. El coeficiente de restitución.$${\ displaystyle e} relaciona la velocidad relativa precolisión $${\ displaystyle \ mathbf {v} _ {r} = \ mathbf {v} _ {p2} - \ mathbf {v} _ {p1}} del punto de contacto a la velocidad relativa post-colisión $${\ displaystyle \ mathbf {v '} _ {r} = \ mathbf {v'} _ {p2} - \ mathbf {v '} _ {p1}} a lo largo del contacto normal $${\ displaystyle \ mathbf {\ hat {n}}} como sigue

$${\ displaystyle \ mathbf {v '} _ {r} \ cdot \ mathbf {\ hat {n}} = -e \ mathbf {v} _ {r} \ cdot \ mathbf {\ hat {n}}}

(4)

Sustituyendo las ecuaciones (1a), (1b), (2a), (2b) y (3) en la ecuación (4) y resolviendo la magnitud del impulso de reacción $${\ displaystyle j_ {r}} rendimientos

$${\ displaystyle j_ {r} = {\ frac {- (1 + e) ​​\ mathbf {v} _ {r} \ cdot \ mathbf {\ hat {n}}} {{m_ {1}} ^ {- 1 } + {m_ {2}} ^ {- 1} + ({\ mathbf {I} _ {1}} ^ {- 1} (\ mathbf {r} _ {1} \ times \ mathbf {\ hat {n }}) \ times \ mathbf {r} _ {1} + {\ mathbf {I} _ {2}} ^ {- 1} (\ mathbf {r} _ {2} \ times \ mathbf {\ hat {n }}) \ times \ mathbf {r} _ {2}) \ cdot \ mathbf {\ hat {n}}}}}

(5)

^[1]

Cálculo de reacción a base de impulso [ editar ]

Así, el procedimiento para calcular las velocidades lineales posteriores a la colisión. $${\ displaystyle \ mathbf {v '} _ {i}} y velocidades angulares $${\ displaystyle \ mathbf {\ omega '} _ {i}} es como sigue:

1. Calcular la magnitud del impulso de reacción. $${\ displaystyle j_ {r}} en términos de $${\ displaystyle \ mathbf {v} _ {r}}, $${\ displaystyle m_ {1}}, $${\ displaystyle m_ {2}}, $${\ displaystyle \ mathbf {I} _ {1}}, $${\ displaystyle \ mathbf {I} _ {2}}, $${\ displaystyle \ mathbf {r} _ {1}}, $${\ displaystyle \ mathbf {r} _ {2}}, $${\ displaystyle \ mathbf {\ hat {n}}} y $${\ displaystyle e}utilizando la ecuación (5)
2. Calcular el vector de impulso de reacción. $${\ displaystyle \ mathbf {j} _ {r}} en términos de su magnitud $${\ displaystyle j_ {r}} y contacto normal $${\ displaystyle \ mathbf {\ hat {n}}}utilizando $${\ displaystyle \ mathbf {j} _ {r} = j_ {r} \ mathbf {\ hat {n}}}.
3. Calcular nuevas velocidades lineales. $${\ displaystyle \ mathbf {v '} _ {i}} en términos de velocidades antiguas $${\ displaystyle \ mathbf {v} _ {i}}misas $${\ displaystyle m_ {i}} y vector de impulso de reacción $${\ displaystyle \ mathbf {j} _ {r}} utilizando las ecuaciones (1a) y (1b)
4. Calcular nuevas velocidades angulares. $${\ displaystyle \ mathbf {\ omega '} _ {i}} en términos de antiguas velocidades angulares $${\ displaystyle \ mathbf {\ omega} _ {i}}tensores de inercia $${\ displaystyle \ mathbf {I} _ {i}} y impulso de reacción $${\ displaystyle j_ {r}} utilizando las ecuaciones (2a) y (2b)

Basado en Impulse modelo de fricción [ editar ]

Modelo de fricción de Coulomb - cono de fricción

Uno de los modelos más populares para describir la fricción es el modelo de fricción de Coulomb . Este modelo define los coeficientes de fricción estática. $${\ displaystyle {\ mu} _ {s} \ in \ mathbb {R}}y fricción dinámica $${\ displaystyle {\ mu} _ {d} \ in \ mathbb {R}} tal que {\ displaystyle {\ mu} _ {s}> {\ mu} _ {d}}. Estos coeficientes describen los dos tipos de fuerzas de fricción en términos de las fuerzas de reacción que actúan sobre los cuerpos. Más específicamente, las magnitudes de fuerza de fricción estáticas y dinámicas$${\ displaystyle f_ {s}, f_ {d} \ in \ mathbb {R}} se calculan en términos de la magnitud de la fuerza de reacción $${\ displaystyle f_ {r} = | \ mathbf {f} _ {r} |} como sigue

	$${\ displaystyle f_ {s} = {\ mu} _ {s} f_ {r}}	(6a)
	$${\ displaystyle f_ {d} = {\ mu} _ {d} f_ {r}}	(6b)

El valor $${\ displaystyle f_ {s}}define una magnitud máxima para la fuerza de fricción requerida para contrarrestar el componente tangencial de cualquier fuerza de suma externa aplicada en un cuerpo relativamente estático, de modo que permanezca estático. Por lo tanto, si la fuerza externa es lo suficientemente grande, la fricción estática es incapaz de contrarrestar completamente esta fuerza, en cuyo punto el cuerpo gana velocidad y queda sujeto a una fricción dinámica de magnitud$${\ displaystyle f_ {d}} Actuando contra la velocidad de deslizamiento.

El modelo de fricción de Coulomb define efectivamente un cono de fricción dentro del cual el componente tangencial de una fuerza ejercida por un cuerpo en la superficie de otro en contacto estático, es contrarrestado por una fuerza igual y opuesta de tal manera que la configuración estática se mantiene. A la inversa, si la fuerza cae fuera del cono, la fricción estática da paso a la fricción dinámica.

Dado el contacto normal $${\ displaystyle \ mathbf {\ hat {n}} \ in \ mathbb {R} ^ {3}} y velocidad relativa $${\ displaystyle \ mathbf {v} _ {r} \ in \ mathbb {R} ^ {3}} del punto de contacto, un vector tangente. $${\ displaystyle \ mathbf {\ hat {t}} \ in \ mathbb {R} ^ {3}}ortogonal a $${\ displaystyle \ mathbf {\ hat {n}}}, se puede definir de tal manera que

{\ displaystyle \ mathbf {\ hat {t}} = \ left \ {{\ begin {matrix} {\ frac {\ mathbf {v} _ {r} - (\ mathbf {v} _ {r} \ cdot \ mathbf {\ hat {n}}) \ mathbf {\ hat {n}}} {| \ mathbf {v} _ {r} - (\ mathbf {v} _ {r} \ cdot \ mathbf {\ hat {n }}) \ mathbf {\ hat {n}}}}} & \ mathbf {v} _ {r} \ cdot \ mathbf {\ hat {n}} \ neq 0 & \\ {\ frac {\ mathbf {f} _ {e} - (\ mathbf {f} _ {e} \ cdot \ mathbf {\ hat {n}}) \ mathbf {\ hat {n}}} {| \ mathbf {f} _ {e} - ( \ mathbf {f} _ {e} \ cdot \ mathbf {\ hat {n}}) \ mathbf {\ hat {n}} |}} & \ mathbf {v} _ {r} \ cdot \ mathbf {\ hat {n}} = 0 & \ mathbf {f} _ {e} \ cdot \ mathbf {\ hat {n}} \ neq 0 \\\ mathbf {0} & \ mathbf {v} _ {r} \ cdot \ mathbf {\ hat {n}} = 0 & \ mathbf {f} _ {e} \ cdot \ mathbf {\ hat {n}} = 0 \\\ end {matrix}} \ right.}

(7)

dónde $${\ displaystyle \ mathbf {f} _ {e} \ in \ mathbb {R} ^ {3}}Es la suma de todas las fuerzas externas sobre el cuerpo. La definición de múltiples casos de$${\ displaystyle \ mathbf {\ hat {t}}} se requiere para calcular de manera robusta la fuerza de fricción real $${\ displaystyle \ mathbf {f} _ {f} \ in \ mathbb {R} ^ {3}}Tanto para el estado de contacto general como para el particular. Informalmente, el primer caso calcula el vector tangente a lo largo del componente de velocidad relativa perpendicular al contacto normal$${\ displaystyle \ mathbf {\ hat {n}}}. Si este componente es cero, se deriva el segundo caso.$${\ displaystyle \ mathbf {\ hat {t}}} En términos del componente tangente de la fuerza externa. $${\ displaystyle \ mathbf {f} _ {e} \ in \ mathbb {R} ^ {3}}. Si no hay velocidad tangencial o fuerzas externas, entonces no se asume ninguna fricción, y$${\ displaystyle \ mathbf {\ hat {t}}}se puede establecer en el vector cero. Así,$${\ displaystyle \ mathbf {f} _ {f} \ in \ mathbb {R} ^ {3}} se calcula como

{\ displaystyle \ mathbf {f} _ {f} = \ left \ {{\ begin {matrix} - (\ mathbf {f} _ {e} \ cdot \ mathbf {\ hat {t}}) \ mathbf {\ hat {t}} & \ mathbf {v} _ {r} \ cdot \ mathbf {\ hat {t}} = 0 & \ mathbf {f} _ {e} \ cdot \ mathbf {\ hat {t}} \ leq f_ {s} \\ - f_ {d} \ mathbf {\ hat {t}} & {\ text {(de lo contrario)}} \\\ end {matrix}} \ right.}

(8)

Las ecuaciones (6a), (6b), (7) y (8) describen el modelo de fricción de Coulomb en términos de fuerzas. Al adaptar el argumento de los impulsos instantáneos, se puede derivar una versión basada en impulsos del modelo de fricción de Coulomb, que relaciona un impulso de fricción$${\ displaystyle \ mathbf {j} _ {f} \ in \ mathbb {R} ^ {3}}, actuando a lo largo de la tangente $${\ displaystyle \ mathbf {\ hat {t}}}, al impulso de reacción $${\ displaystyle \ mathbf {j} _ {r} \ in \ mathbb {R} ^ {3}}. Integración (6a) y (6b) en el intervalo de tiempo de colisión$${\ displaystyle [t_ {0} .. t_ {1}]} rendimientos

	$${\ displaystyle j_ {s} = {\ mu} _ {s} j_ {r}}	(9a)
	$${\ displaystyle j_ {d} = {\ mu} _ {d} j_ {r}}	(9b)

dónde $${\ displaystyle j_ {r} = | \ mathbf {j} _ {r} |} Es la magnitud del impulso de reacción que actúa a lo largo del contacto normal. $${\ displaystyle \ mathbf {\ hat {n}}}. Del mismo modo, al asumir$${\ displaystyle \ mathbf {\ hat {t}}} constante a lo largo del intervalo de tiempo, la integración de (8) rendimientos

{\ displaystyle \ mathbf {j} _ {f} = \ left \ {{\ begin {matrix} - (m \ mathbf {v} _ {r} \ cdot \ mathbf {\ hat {t}}) \ mathbf { \ hat {t}} & \ mathbf {v} _ {r} \ cdot \ mathbf {\ hat {t}} = 0 & m \ mathbf {v} _ {r} \ cdot \ mathbf {\ hat {t}} \ leq j_ {s} \\ - j_ {d} \ mathbf {\ hat {t}} & {\ text {(de lo contrario)}} \\\ end {matrix}} \ right.}

(10)

Las ecuaciones (5) y (10) definen un modelo de contacto basado en impulsos que es ideal para simulaciones basadas en impulsos. Al usar este modelo, se debe tener cuidado en la elección de$${\ displaystyle {\ mu} _ {s}} y $${\ displaystyle {\ mu} _ {d}} como valores más altos pueden introducir energía cinética adicional en el sistema.

La aeroacústica computacional es una rama de la aeroacústica que tiene como objetivo analizar la generación de ruido mediante flujos turbulentos a través de métodos numéricos.

Historia [ editar ]

El origen de la aeroacústica computacional solo se remonta a mediados de la década de 1980, con una publicación de Hardin y Lamkin ^[1] que afirmó que

" [...] el campo de la mecánica de fluidos computacional ha estado avanzando rápidamente en los últimos años y ahora ofrece la esperanza de que" aeroacústica computacional ", donde el ruido se computa directamente desde una primera determinación de principios de campos de velocidad y vorticidad, pueda sea ​​posible, [...] "

Más tarde, en una publicación de 1986 ^[2], los mismos autores introdujeron la abreviatura CAA. El término se usó inicialmente para un enfoque de número de Mach bajo (Expansión del campo de perturbación acústica sobre un flujo incompresible) como se describe en EIF . Más tarde, a principios de la década de 1990, la creciente comunidad de CAA tomó el término y lo usó ampliamente para cualquier tipo de método numérico que describiera la radiación de ruido de una fuente aeroacústica o la propagación de ondas de sonido en un campo de flujo no homogéneo. Dichos métodos numéricos pueden ser métodos de integración de campo lejano (por ejemplo, FW-H ^[3] [4] ), así como métodos numéricos directos optimizados para las soluciones (por ejemplo, ^[5]) de un modelo matemático que describe la generación y / o propagación de ruido aerodinámico. Con el rápido desarrollo de los recursos computacionales, este campo ha experimentado un progreso espectacular durante las últimas tres décadas.

Métodos [ editar ]

Enfoque de simulación numérica directa (DNS) para CAA [ editar ]

La ecuación compresible de Navier-Stokes describe tanto el campo de flujo como el campo acústico generado aerodinámicamente. Así ambos pueden resolverse directamente. Esto requiere una resolución numérica muy alta debido a las grandes diferencias en la escala de longitud presente entre las variables acústicas y las variables de flujo. Es computacionalmente muy exigente e inadecuado para cualquier uso comercial.

Enfoque híbrido [ editar ]

En este enfoque, el dominio computacional se divide en diferentes regiones, de modo que el campo acústico o de flujo gobernante se puede resolver con diferentes ecuaciones y técnicas numéricas. Esto implicaría utilizar dos solucionadores numéricos diferentes, primero una herramienta dedicada de dinámica de fluidos computacional(CFD) y, en segundo lugar, un solucionador acústico. El campo de flujo se utiliza para calcular las fuentes acústicas. Se pueden utilizar soluciones de campo de fluidos de estado estable (RANS, SNGR (generación de ruido estocástico y radiación), ...) y transitorias (DNS, LES, DES, URANS, ...). Estas fuentes acústicas se proporcionan al segundo solucionador que calcula la propagación acústica. La propagación acústica se puede calcular utilizando uno de los siguientes métodos:

1. Métodos integrales
   1. Analogía de lighthill
   2. Kirchhoff integral
   3. FW-H
2. SOTAVENTO
3. Pseudospectral
4. EIF
5. MONO

Métodos integrales [ editar ]

Existen múltiples métodos, que se basan en una solución conocida de la ecuación de onda acústica para calcular el campo lejano acústico de una fuente de sonido. Debido a que una solución general para la propagación de ondas en el espacio libre se puede escribir como una integral en todas las fuentes, estas soluciones se resumen como métodos integrales. Las fuentes acústicas deben ser conocidas de alguna fuente diferente (por ejemplo, una simulación de elementos finitos de un sistema mecánico en movimiento o una simulación CFD dinámica de las fuentes en un medio móvil). La integral se toma sobre todas las fuentes en el tiempo retardado (tiempo de la fuente), que es el momento en el que la fuente envía la señal, que llega ahora a una posición de observador determinada. Común a todos los métodos integrales es, que no pueden explicar los cambios en la velocidad del sonido o la velocidad de flujo promedio entre la fuente y la posición del observador, ya que utilizan una solución teórica de la ecuación de onda. Al aplicar la teoría de Lighthill.^[6] [7]Para las ecuaciones de la mecánica de fluidos de Navier Stokes, uno obtiene fuentes volumétricas, mientras que las otras dos analogías proporcionan la información de campo lejano basada en una integral de superficie. Las analogías acústicas pueden ser muy eficientes y rápidas, ya que se utiliza la solución conocida de la ecuación de onda. Un observador lejano toma tanto tiempo como un observador muy cercano. Común para la aplicación de todas las analogías es la integración en un gran número de contribuciones, lo que puede llevar a problemas numéricos adicionales (suma / resta de muchos números grandes con un resultado cercano a cero). Además, cuando se aplica un método integral, generalmente la fuente El dominio está limitado de alguna manera. Mientras que en teoría las fuentes externas deben ser cero, la aplicación no siempre puede cumplir esta condición. Especialmente en relación con las simulaciones de CFD, esto conduce a grandes errores de corte.

La analogía de Lighthill [ editar ]

También llamada ' Analogía Acústica '. Para obtener la analogía aeroacústica de Lighthill, se reorganizan las ecuaciones de Navier-Stokes. El lado izquierdo es un operador de onda, que se aplica a la perturbación de densidad o perturbación de presión respectivamente. El lado derecho se identifica como las fuentes acústicas en un flujo de fluido, entonces. Como la analogía de Lighthill se sigue directamente de las ecuaciones de Navier-Stokes sin simplificación, todas las fuentes están presentes. Algunas de las fuentes se identifican como ruido turbulento o laminar. La presión de sonido de campo lejano se da entonces en términos de una integral de volumen sobre el dominio que contiene la fuente de sonido. El término fuente siempre incluye fuentes físicas y tales fuentes, que describen la propagación en un medio no homogéneo.

El operador de onda de la analogía de Lighthill está limitado a condiciones de flujo constante fuera de la zona de origen. No se permite variación de densidad, velocidad de sonido y número de Mach. Las diferentes condiciones de flujo medio se identifican como fuentes fuertes con signo opuesto por la analogía, una vez que una onda acústica la pasa. Parte de la onda acústica es eliminada por una fuente y se irradia una nueva onda para fijar la velocidad de onda diferente. Esto a menudo conduce a volúmenes muy grandes con fuentes fuertes. Se han propuesto varias modificaciones a la teoría original de Lighthill para explicar la interacción sonido-flujo u otros efectos. Para mejorar la analogía de Lighthill, las siguientes analogías consideran diferentes cantidades dentro del operador de onda y diferentes operadores de onda. Todos ellos obtienen términos fuente modificados, lo que a veces permite una visión más clara de las fuentes "reales". Las analogías acústicas de Lilley,^[8] Pierce, ^[9] Howe^[10] y Möhring ^[11] son solo algunos ejemplos de analogías aeroacústicas basadas en las ideas de Lighthill. Todas las analogías acústicas requieren una integración de volumen sobre un término fuente.

La principal dificultad con la analogía acústica, sin embargo, es que la fuente de sonido no es compacta en el flujo supersónico. Se pueden encontrar errores en el cálculo del campo de sonido, a menos que el dominio computacional se pueda extender en la dirección descendente más allá de la ubicación donde la fuente de sonido se ha deteriorado por completo. Además, una explicación precisa del efecto del tiempo retardado requiere mantener un registro largo del historial de tiempo de las soluciones convergentes de la fuente de sonido, lo que nuevamente representa un problema de almacenamiento. Para problemas realistas, el almacenamiento requerido puede alcanzar el orden de 1 terabyte de datos.

Kirchhoff integral [ editar ]

Kirchhoff y Helmholtzmostró que la radiación de sonido de una región de fuente limitada puede describirse encerrando esta región de fuente por una superficie de control, la llamada superficie de Kichhoff. Luego, el campo de sonido dentro o fuera de la superficie, donde no se permiten fuentes y se aplica el operador de onda en el lado izquierdo, se puede producir como una superposición de monopolos y dipolos en la superficie. La teoría sigue directamente de la ecuación de onda. La intensidad de la fuente de los monopolos y dipolos en la superficie se puede calcular si se conoce la velocidad normal (para los monopolos) y la presión (para los dipolos) en la superficie, respectivamente. Una modificación del método permite incluso calcular la presión sobre la superficie basándose únicamente en la velocidad normal. La velocidad normal podría ser dada por una simulación FE de una estructura en movimiento, por ejemplo. Sin embargo, La modificación para evitar la presión acústica en la superficie a ser conocida conduce a problemas cuando se considera un volumen cerrado a sus frecuencias resonantes, que es un problema importante de las implementaciones de su método. El método integral de Kirchhoff encuentra, por ejemplo, la aplicación enMétodos de elementos de frontera (BEM). Una velocidad de flujo no nula se contabiliza considerando un marco de referencia móvil con la velocidad de flujo exterior, en la que tiene lugar la propagación de la onda acústica. Las aplicaciones repetitivas del método pueden dar cuenta de los obstáculos. Primero se calcula el campo de sonido en la superficie del obstáculo y luego se introduce el obstáculo agregando fuentes en su superficie para cancelar la velocidad normal en la superficie del obstáculo. Las variaciones del campo de flujo promedio (velocidad del sonido, densidad y velocidad) se pueden tener en cuenta mediante un método similar (por ejemplo, BEM de doble reciprocidad).

FW-H [ editar ]

El método de integración de Ffowcs Williams y Hawkings se basa en la analogía acústica de Lighthill. Sin embargo, por algunas modificaciones matemáticas bajo el supuesto de una región de fuente limitada, que está encerrada por una superficie de control (superficie FW-H), se evita la integral de volumen. Las integrales de superficie sobre fuentes monopolares y dipolo permanecen. A diferencia del método de Kirchhoff, estas fuentes se derivan directamente de las ecuaciones de Navier-Stokes a través de la analogía de Lighthill. Las fuentes fuera de la superficie FW-H pueden contabilizarse mediante una integral de volumen adicional sobre las fuentes cuadrupolares que siguen del Tensor de Lighthill. Sin embargo, al considerar los mismos supuestos de la teoría lineal de Kirchhoff, el método FW-H es igual al método de Kirchhoff.

Ecuaciones de Euler linealizadas [ editar ]

Considerando pequeñas perturbaciones superpuestas a un flujo de densidad promedio uniforme $${\ displaystyle \ rho _ {0}}, presión $${\ displaystyle p_ {0}} y velocidad en el eje x $${\ displaystyle u_ {0}}, las ecuaciones de Euler para un modelo bidimensional se presentan como:

$${\ displaystyle {\ frac {\ partial \ mathbf {U}} {\ partial t}} + {\ frac {\ partial \ mathbf {F}} {\ partial x}} + {\ frac {\ partial \ mathbf { G}} {\ parcial y}} = \ mathbf {S}},

dónde

$${\ displaystyle \ mathbf {U} = {\ begin {bmatrix} \ rho \\ u \\ v \\ p \\\ end {bmatrix}} \, \ \ mathbf {F} = {\ begin {bmatrix} \ rho _ {0} u + \ rho u_ {0} \\ u_ {0} u + p / \ rho _ {0} \\ u_ {0} v \\ u_ {0} p + \ gamma p_ {0} u \ \\ end {bmatrix}} \, \ \ mathbf {G} = {\ begin {bmatrix} \ rho _ {0} v \\ 0 \\ p / \ rho _ {0} \\\ gamma p_ {0} v \\\ end {bmatrix}},}

dónde $${\ displaystyle \ rho}, $${\ displaystyle u}, $${\ displaystyle v} y $${\ displaystyle p} son las variables de campo acústico, $${\ displaystyle \ gamma} La proporción de calores específicos. $${\ displaystyle c_ {p} / c_ {v}}, para aire a 20 ° C $${\ displaystyle c_ {p} / c_ {v} = 1.4}, y el término fuente $${\ displaystyle \ mathbf {S}}en el lado derecho representa fuentes inestables distribuidas. La aplicación de LEE se puede encontrar en los estudios de ruido del motor. ^[12]

Para flujos de números de Mach altos en regímenes compresibles, la propagación acústica puede verse influida por no linealidades y el LEE ya no puede ser el modelo matemático apropiado.

Pseudospectral [ editar ]

Se puede aplicar un método pseudospectral de dominio de tiempo de Fourier a los problemas de propagación de ondas pertinentes a los aeroacústicos computacionales. El algoritmo original del método de dominio de tiempo pseudo espectral de Fourier funciona para problemas periódicos sin la interacción con límites físicos. Se ha propuesto una condición de límite de pared de deslizamiento, combinada con una técnica de zona de amortiguamiento para resolver algunos problemas aeroacústicos no periódicos. ^[13] En comparación con otros métodos computacionales, se prefiere el método pseudospectral por su alta precisión de orden.

EIF [ editar ]

Expansión sobre el flujo incompresible.

APE [ editar ]

Ecuaciones de perturbación acústica

Consulte el artículo "Ecuaciones de perturbación acústica basadas en la descomposición del flujo mediante el filtrado de fuente" por R.Ewert y W.Schroder.