MECÁNICA

El torque de fricción es el torque causado por la fuerza de fricciónque se produce cuando dos objetos en contacto se mueven. Como todos los pares de torsión, es una fuerza de rotación que se puede medir en metros de newton o en libras-pies.

Ingeniería [ editar ]

El par de fricción puede ser disruptivo en la ingeniería . Hay una variedad de medidas que los ingenieros pueden elegir para eliminar estas interrupciones. Los rodamientos de bolas son un ejemplo de un intento de minimizar el par de fricción.

El par de fricción también puede ser un activo en ingeniería . Los pernos y tuercas, o los tornillos a menudo están diseñados para sujetarse con un par de torsión dado, donde la fricción es adecuada durante el uso o la operación para que el perno, tuerca o tornillo permanezcan sujetos de manera segura. Esto es cierto con aplicaciones tales como las tuercas de arrastre que sujetan las ruedas a los vehículos, o el equipo sometido a vibración con pernos, tuercas o tornillos suficientemente bien sujetos para evitar que la vibración se suelte.

Ejemplos [ editar ]

• Cuando un ciclista aplica el freno a su rueda delantera , la bicicleta avanza hacia delante debido al par de fricción entre la rueda y el suelo .
• Cuando una pelota de golf toca el suelo, comienza a girar en parte debido al par de fricción aplicado a la pelota de golf debido a la fricción entre la pelota de golf y el suelo.

Esta imagen muestra una situación de ejemplo donde hay un par de fricción activo. La flecha grande del vector negro representa la fuerza primaria que actúa sobre la barra (la línea negra gruesa ), lo que hace que gire alrededor del punto gris en su extremo opuesto que representa un eje . La gran flecha roja del vector representa el par causado por la fuerza primaria. La flecha pequeña de vector negro representa la fuerza de fricción causada por la barra que se desliza a través de la segunda barra (gris).

Las fuerzas generalizadas encuentran uso en la mecánica lagrangiana , donde desempeñan un papel conjugado a las coordenadas generalizadas . Se obtienen de las fuerzas aplicadas, F _i , i = 1, ..., n, que actúan sobre un sistema que tiene su configuración definida en términos de coordenadas generalizadas . En la formulación del trabajo virtual , cada fuerza generalizada es el coeficiente de la variación de una coordenada generalizada.

Trabajo virtual [ editar ]

Las fuerzas generalizadas se pueden obtener a partir del cálculo de la obra virtual , δW, de las fuerzas aplicadas. ^[1] : 265

El trabajo virtual de las fuerzas, F _i , que actúa sobre las partículas P _i , i = 1, ..., n, viene dado por

$${\ displaystyle \ delta W = \ sum _ {i = 1} ^ {n} \ mathbf {F} _ {i} \ cdot \ delta \ mathbf {r} _ {i}}

donde δ r _i es el desplazamiento virtual de la partícula P _i .

Coordenadas generalizadas [ editar ]

Deje que los vectores de posición de cada una de las partículas, r _i , sean una función de las coordenadas generalizadas, q _j , j = 1, ..., m. Entonces los desplazamientos virtuales δ r _i están dados por

$${\ displaystyle \ delta \ mathbf {r} _ {i} = \ sum _ {j = 1} ^ {m} {\ frac {\ partial \ mathbf {r} _ {i}} {\ parcial q_ {j} }} \ delta q_ {j}, \ quad i = 1, \ ldots, n,}

donde δq _j es el desplazamiento virtual de la coordenada generalizada q _j .

El trabajo virtual para el sistema de partículas se convierte en.

$${\ displaystyle \ delta W = \ mathbf {F} _ {1} \ cdot \ sum _ {j = 1} ^ {m} {\ frac {\ partial \ mathbf {r} _ {1}} {\ parcial q_ {j}}} \ delta q_ {j} + \ ldots + \ mathbf {F} _ {n} \ cdot \ sum _ {j = 1} ^ {m} {\ frac {\ partial \ mathbf {r} _ {n}} {\ parcial q_ {j}}} \ delta q_ {j}.}

Recoge los coeficientes de δq _j para que

$${\ displaystyle \ delta W = \ sum _ {i = 1} ^ {n} \ mathbf {F} _ {i} \ cdot {\ frac {\ partial \ mathbf {r} _ {i}} {\ partial q_ {1}}} \ delta q_ {1} + \ ldots + \ sum _ {i = 1} ^ {n} \ mathbf {F} _ {i} \ cdot {\ frac {\ partial \ mathbf {r} _ {i}} {\ partial q_ {m}}} \ delta q_ {m}.}

Fuerzas generalizadas [ editar ]

El trabajo virtual de un sistema de partículas se puede escribir en la forma

$${\ displaystyle \ delta W = Q_ {1} \ delta q_ {1} + \ ldots + Q_ {m} \ delta q_ {m},}

dónde

$${\ displaystyle Q_ {j} = \ sum _ {i = 1} ^ {n} \ mathbf {F} _ {i} \ cdot {\ frac {\ partial \ mathbf {r} _ {i}} {\ parcial q_ {j}}}, \ quad j = 1, \ ldots, m,}

se denominan fuerzas generalizadas asociadas con las coordenadas generalizadas q _j , j = 1, ..., m.

Formulación de la velocidad [ editar ]

En la aplicación del principio de trabajo virtual, a menudo es conveniente obtener desplazamientos virtuales de las velocidades del sistema. Para el sistema de n partículas, deje que la velocidad de cada partícula P _i sea V _i , entonces el desplazamiento virtual δ r _i también se puede escribir en la forma ^[2]

$${\ displaystyle \ delta \ mathbf {r} _ {i} = \ sum _ {j = 1} ^ {m} {\ frac {\ partial \ mathbf {V} _ {i}} {\ partial {\ dot { q}} _ {j}}} \ delta q_ {j}, \ quad i = 1, \ ldots, n.}

Esto significa que la fuerza generalizada, Q _j , también se puede determinar como

$${\ displaystyle Q_ {j} = \ sum _ {i = 1} ^ {n} \ mathbf {F} _ {i} \ cdot {\ frac {\ partial \ mathbf {V} _ {i}} {\ parcial {\ dot {q}} _ {j}}}, \ quad j = 1, \ ldots, m.}

Principio de d'Alembert [ editar ]

D'Alembert formuló la dinámica de una partícula como el equilibrio de las fuerzas aplicadas con una fuerza de inercia ( fuerza aparente ), llamada principio de D'Alembert . La fuerza de inercia de una partícula, P _i , de masa m _i es

$${\ displaystyle \ mathbf {F} _ {i} ^ {*} = - m_ {i} \ mathbf {A} _ {i}, \ quad i = 1, \ ldots, n,}

donde A _i es la aceleración de la partícula.

Si la configuración del sistema de partículas depende de las coordenadas generalizadas q _j , j = 1, ..., m, entonces la fuerza de inercia generalizada viene dada por

$${\ displaystyle Q_ {j} ^ {*} = \ sum _ {i = 1} ^ {n} \ mathbf {F} _ {i} ^ {*} \ cdot {\ frac {\ partial \ mathbf {V} _ {i}} {\ partial {\ dot {q}} _ {j}}}, \ quad j = 1, \ ldots, m.}

La forma de D'Alembert del principio de rendimiento de trabajo virtual.

$${\ displaystyle \ delta W = (Q_ {1} + Q_ {1} ^ {*}) \ delta q_ {1} + \ ldots + (Q_ {m} + Q_ {m} ^ {*}) \ delta q_ {metro}.}

La geomecánica (del prefijo griego geo- significado " tierra " y " mecánica ") implica el estudio geológico del comportamiento del suelo y la roca .

Las dos principales disciplinas de la geomecánica son la mecánica de suelos y la mecánica de rocas . El primero trata el comportamiento del suelo desde una escala pequeña hasta una escala de deslizamiento de tierra . Este último se ocupa de problemas en geociencias relacionadas con la caracterización de la masa rocosa y la mecánica de la masa rocosa, como la aplicada a la industria petrolera o grandes profundidades, el diseño de túneles, la ruptura de rocas y la perforación de rocas. ^[1]

Muchos aspectos de la geomecánica se superponen con partes de ingeniería geotécnica , geología de ingenieríae ingeniería geológica. Los desarrollos modernos se relacionan con la sismología , la mecánica de continuidad , la mecánica discontinua y los fenómenos de transporte.

En la industria de la ingeniería petrolera, la geomecánica se usa para predecir parámetros importantes, como las tensiones de roca in situ, el módulo de elasticidad, el coeficiente de fuga y la relación de Poisson. Los parámetros del yacimiento que incluyen: la porosidad de la formación, la permeabilidad y la presión del fondo del pozo se pueden derivar de la evaluación geomecánica. El ingeniero geotécnico o geofísico se basa en varias técnicas para obtener modelos geomecánicos confiables. Estas técnicas que han evolucionado a lo largo de los años, son: extracción de muestras, análisis de registros; métodos de prueba de pozos como fracturamiento hidráulico y métodos de sonar geofísico como la emisión acústica.

 tren de gravedad es un medio de transporte teórico destinado a ir entre dos puntos en la superficie de una esfera , siguiendo un túnel recto que va directamente de un punto a otro a través del interior de la esfera.

En un cuerpo grande como un planeta , se podría dejar que este tren acelere utilizando solo la fuerza de la gravedad , ya que durante la primera mitad del viaje (desde el punto de partida hasta el centro), el impulso hacia abajo hacia el centro de gravedad Lo tiraría hacia el destino. Durante la segunda mitad del viaje, la aceleración sería en la dirección opuesta a la trayectoria, pero (ignorando los efectos de la fricción ) la velocidad adquirida antes sería suficiente para cancelar esta desaceleración exactamente (para que el tren llegue a su destino). con velocidad igual a cero).

En realidad, hay dos razones por las que los trenes de gravedad no existen. Primero, una larga distancia de tránsito perforaría el manto de la Tierra y atravesaría una región donde la roca es más fluida que sólida. No se conocen materiales que resistan el tremendo calor y la presión en el núcleo interno . La temperatura se estima en 5,700 K (5,430 ° C; 9,800 ° F) y la presión tan alta como de 330 a 360 gigapascales (3,300,000 a 3,600,000 atm). En segundo lugar, las pérdidas por fricción serían significativas. Las pérdidas por fricción de rodadura podrían reducirse utilizando un tren levitado magnéticamente . Sin embargo, a menos que se evacúe todo el aire del túnel, las pérdidas por fricción debidas a la resistencia del aire harían inutilizable el tren de gravedad. Evacuando el ambiente para convertirlo en unvactrain eliminaría esta resistencia, pero requeriría una potencia adicional. Tales objeciones no se aplicarían a planetas y lunas sólidas que no tienen una atmósfera.

Origen del concepto [ editar ]

En el siglo XVII, el científico británico Robert Hooke presentó la idea de un objeto acelerado dentro de un planeta en una carta a Isaac Newton . Un proyecto de tren de gravedad fue presentado seriamente a la Academia de Ciencias de París en el siglo XIX. La misma idea fue propuesta, sin cálculo, por Lewis Carroll en 1893 en Sylvie y Bruno concluyó . La idea se redescubrió en la década de 1960 cuando el físico Paul Cooper publicó un artículo en el American Journal of Physics que sugiere que los trenes de gravedad se consideren para un futuro proyecto de transporte. ^[2]

Consideraciones matemáticas [ editar ]

Bajo el supuesto de un planeta esférico con densidad uniforme, e ignorando los efectos relativistas y la fricción, un tren de gravedad tiene las siguientes propiedades: ^[3]

• La duración de un viaje depende solo de la densidad del planeta y de la constante gravitacional , pero no del diámetro del planeta.
• La velocidad máxima se alcanza en el punto medio de la trayectoria.

Para los trenes de gravedad entre puntos que no son las antípodas entre sí, se sostienen los siguientes:

• El túnel de tiempo más corto a través de una tierra homogénea es un hipocicloide ; En el caso especial de dos puntos antipodales, el hipocicloide se degenera en una línea recta.
• Todos los trenes de gravedad en línea recta en un planeta dado toman exactamente la misma cantidad de tiempo para completar un viaje (es decir, sin importar dónde se encuentren los dos puntos finales de su trayectoria en la superficie).

Específicamente en el planeta Tierra , dado que el movimiento de un tren de gravedad es la proyección de un movimiento de satélite de órbita terrestre muy baja en una línea, tiene los siguientes parámetros:

• El tiempo de viaje es igual a 2530.30 segundos (casi 42.2 minutos, la mitad del período de un satélite de la órbita terrestre baja), suponiendo que la Tierra fuera una esfera perfecta de densidad uniforme.
• Al tomar en cuenta la distribución de densidad realista dentro de la Tierra, como se conoce en el Modelo de Tierra Preliminar de Referencia , el tiempo esperado de caída se reduce de 42 a 38 minutos. ^[4]
• Para un tren que atraviesa directamente el centro de la Tierra, la velocidad máxima es la primera velocidad cósmica, aproximadamente 7.900 metros por segundo (28440 km / h) ( Mach 23.2).

Para poner algunos números en perspectiva, el orificio de perforación más profundo de la corriente es el Kola Superdeep Borehole con una profundidad real de 12,262 metros. Mientras que para cubrir una distancia entre Londres y París (350 km) a través de un camino hipocicloidal se necesitaría la creación de un agujero de 55,704 metros de profundidad. Esta profundidad no es solo 4.5 veces más profunda; También necesitará un túnel que pase dentro del manto de la Tierra .

Derivación matemática [ editar ]

Usando las aproximaciones que la Tierra es perfectamente esférica y de densidad uniforme. $${\ displaystyle \ rho}, y el hecho de que dentro de una esfera hueca uniforme no hay gravedad, la aceleración gravitacional$${\ displaystyle a} experimentado por un cuerpo dentro de la Tierra es proporcional a la proporción de la distancia desde el centro $${\ displaystyle r} al radio de la tierra $${\ displaystyle R}. Esto es porque el metro a distancia$${\ displaystyle r} desde el centro es como estar en la superficie de un planeta de radio $${\ displaystyle r}, dentro de una esfera hueca que no aporta nada.

$${\ displaystyle a = {\ frac {GM} {r ^ {2}}} = {\ frac {G \ rho V} {r ^ {2}}} = {\ frac {G \ rho {\ frac {4 } {3}} \ pi \, r ^ {3}} {r ^ {2}}} = G \ rho {\ frac {4} {3}} \ pi \, r}

En la superficie, $${\ displaystyle r = R}, así que la aceleración gravitacional es $${\ displaystyle g = G \ rho {\ frac {4} {3}} \ pi \, R}. Por lo tanto, la aceleración gravitacional en$${\ displaystyle r} es

$${\ displaystyle a = {\ frac {r} {R}} \, g}

Ruta diamétrica a las antípodas [ editar ]

En el caso de una línea recta a través del centro de la Tierra, la aceleración del cuerpo es igual a la de la gravedad: está cayendo libremente hacia abajo. Empezamos a caer a la superficie, así que a la hora.$${\ displaystyle t} (Tratando la aceleración y la velocidad como positiva hacia abajo):

$${\ displaystyle r_ {t} = R- \ int _ {0} ^ {t} v_ {t} \, dt = R- \ int _ {0} ^ {t} \ int _ {0} ^ {t} a_ {t} \, dt \, dt}

Diferenciando dos veces:

$${\ displaystyle {\ frac {d ^ {2} r} {dt ^ {2}}} = - a_ {t} = - {\ frac {r} {R}} \, g = - \ omega ^ {2 } \, r}

dónde $${\ displaystyle \ omega = {\ sqrt {\ frac {g} {R}}}}. Esta clase de problemas, donde existe una fuerza de restauración proporcional al desplazamiento lejos de cero, tiene soluciones generales de la forma.$${\ displaystyle r = k \ cos (\ omega t + \ varphi)}, y describe el movimiento armónico simple como en un resorte o péndulo .

En este caso $${\ displaystyle r_ {t} = R \ cos {\ sqrt {\ frac {g} {R}}} \, t} así que eso $${\ displaystyle r_ {0} = R}, comenzamos en la superficie en el tiempo cero y oscilamos de un lado a otro para siempre.

El tiempo de viaje a las antípodas es la mitad de un ciclo de este oscilador, que es el momento para que el argumento $${\ displaystyle \ cos {\ sqrt {\ frac {g} {R}}} \, t} para barrer $${\ displaystyle {\ pi}}radianes Usando aproximaciones simples de$${\ displaystyle g = 10 {\ text {m}} / {\ text {s}} ^ {2}, R = 6500 {\ text {km}}}ese tiempo es

$${\ displaystyle T = {\ frac {\ pi} {\ omega}} = {\ frac {\ pi} {\ sqrt {\ frac {g} {R}}}} \ approx {\ frac {3.1415926} {\ sqrt {\ frac {10} {6500000}}}} \ approx 2532 {\ text {s}}}

Ruta recta entre dos puntos arbitrarios [ editar ]

Tren de la trayectoria de la gravedad

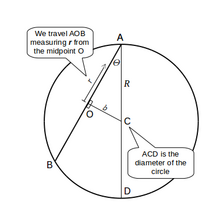
Para el caso más general de la trayectoria en línea recta entre dos puntos cualquiera en la superficie de una esfera, calculamos la aceleración del cuerpo a medida que se mueve sin fricción a lo largo de su trayectoria recta.

El cuerpo viaja a lo largo de AOB, siendo O el punto medio del camino y el punto más cercano al centro de la Tierra en este camino. A distancia$${\ displaystyle r}A lo largo de este camino, la fuerza de la gravedad depende de la distancia. $${\ displaystyle x}al centro de la tierra como arriba. Usando la taquigrafía$${\ displaystyle b = R \ sin \ theta} para longitud OC:

$${\ displaystyle g_ {r} = {\ frac {x} {R}} \, g = {\ frac {\ sqrt {r ^ {2} + b ^ {2}}} {R}} \, g}

La aceleración resultante en el cuerpo, porque está en una superficie inclinada sin fricción , es$${\ displaystyle g_ {r} \ cos \ varphi}:

Diagrama de fuerzas en un tren de gravedad en una línea recta no diametral

$${\ displaystyle a_ {r} = g_ {r} \ cos \ varphi = {\ frac {\ sqrt {r ^ {2} + b ^ {2}}} {R}} \, g \ cos \ varphi}

Pero $${\ displaystyle \ cos \ varphi} es $${\ displaystyle r / x = {\ frac {r} {\ sqrt {r ^ {2} + b ^ {2}}}}}, sustituyendo así:

$${\ displaystyle a_ {r} = {\ frac {\ sqrt {r ^ {2} + b ^ {2}}} {R}} \, g \, {\ frac {r} {\ sqrt {r ^ { 2} + b ^ {2}}}} = {\ frac {r} {R}} \, g}

que es exactamente lo mismo para este nuevo $${\ displaystyle r}, distancia a lo largo de AOB lejos de O, en cuanto a la $${\ displaystyle r}en el caso diametral a lo largo de ACD. Así que el análisis restante es el mismo, acomodando la condición inicial que el máximo$${\ displaystyle r} es $${\ displaystyle R \ cos \ theta = AO} la ecuación completa del movimiento es

$${\ displaystyle r_ {t} = R \ cos \ theta \ cos {\ sqrt {\ frac {g} {R}}} \, t}

La constante de tiempo $${\ displaystyle \ omega = {\ sqrt {\ frac {g} {R}}}}es el mismo que en el caso diametral, por lo que el tiempo de viaje es de 42 minutos; es solo que todas las distancias y velocidades son escaladas por la constante$${\ displaystyle \ cos \ theta}.

Independencia del radio del planeta [ editar ]

La constante de tiempo $${\ displaystyle \ omega} depende solo de $${\ displaystyle {\ frac {g} {R}}} así que si expandimos eso obtenemos

$${\ displaystyle {\ frac {g} {R}} = {\ frac {GM / R ^ {2}} {R}} = {\ frac {GM} {R ^ {3}}} = {\ frac { G \ rho \, V} {R ^ {3}}} = {\ frac {G \ rho \, {\ frac {4} {3}} \ pi \, R ^ {3}} {R ^ {3 }}} = G \ rho \, {\ frac {4} {3}} \ pi}

que depende solo de la constante gravitacional y$${\ displaystyle \ rho}La densidad del planeta. El tamaño del planeta es inmaterial; El tiempo de viaje es el mismo si la densidad es la misma.