MECÁNICA

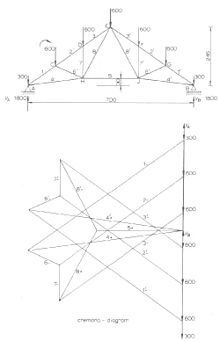
El diagrama de Cremona , también conocido como el método de Cremona- Maxwell , es un método gráfico utilizado en estática de vigaspara determinar las fuerzas en los miembros ( estadística estática ). El método fue desarrollado por el matemático italiano Luigi Cremona . Sin embargo, los diagramas reconocibles de Cremona aparecieron desde 1725, en la obra póstumamente publicada de Pierre Varignon , Nouvelle Méchanique ou Statique . ^[1]

En el método de Cremona, primero se dibujan las fuerzas externas y las reacciones (a escala ) formando una línea vertical en el lado inferior derecho de la imagen. Esta es la suma de todos los vectores de fuerza y es igual a cero ya que existe un equilibrio mecánico .

Dado que el equilibrio se mantiene para las fuerzas externas en toda la construcción del truss, también lo es para las fuerzas internas que actúan en cada articulación. Para que una articulación descanse, la suma de las fuerzas sobre una articulación también debe ser igual a cero. Comenzando en la Aorda conjunta , las fuerzas internas se pueden encontrar dibujando líneas en el diagrama de Cremona que representa las fuerzas en los miembros 1 y 4, yendo en sentido horario; V _A(subiendo) carga en A (bajando), fuerza en el miembro 1 (bajando / izquierda), miembro 4 (subiendo / derecha) y cerrando con V _A. Como la fuerza en el miembro 1 es hacia la articulación, el miembro está bajo compresión, la fuerza en el miembro 4 está lejos de la articulación, por lo que el miembro 4 está bajo tensión. La longitud de las líneas para los miembros 1 y 4 en el diagrama, multiplicada por el factor de escala elegido, es la magnitud de la fuerza en los miembros 1 y 4.

Ahora, de la misma manera, las fuerzas en los miembros 2 y 6 se pueden encontrar para la junta C ; fuerza en el miembro 1 (subiendo / derecha), fuerza en C bajando, fuerza en 2 (bajando / izquierda), fuerza en 6 (subiendo / izquierda) y cerrando con la fuerza en el miembro 1.

Se pueden seguir los mismos pasos para las uniones D , H y E que dan como resultado el diagrama completo de Cremona, donde se conocen las fuerzas internas de todos los miembros.

En una siguiente fase se deben considerar las fuerzas causadas por el viento . El viento causará presión en el lado contra el viento de un techo (y viga) y la succión en el lado del viento. Esto se traducirá en cargas asimétricas, pero el método de Cremona es el mismo. La fuerza del viento puede introducir fuerzas más grandes en los miembros de la armadura individuales que las cargas verticales estáticas.

Diagrama de Cremona para un truss plano.

El estrés cíclico es la distribución de fuerzas (alias estrés) que cambian con el tiempo de manera repetitiva. Como ejemplo, considere una de las ruedas grandes que se utilizan para conducir un elevador aéreo , como un remonte . El cable de alambre enrollado alrededor de la rueda ejerce una fuerza hacia abajo sobre la rueda y el eje de transmisión que soporta la rueda. Aunque el eje, la rueda y el cable se mueven, la fuerza permanece casi vertical con respecto al suelo. Por lo tanto, un punto en la superficie del eje impulsor sufrirá tensión cuando apunta hacia el suelo y se comprime cuando apunta al cielo.

Tipos de estrés cíclico [ editar ]

El esfuerzo cíclico se encuentra con frecuencia en la maquinaria giratoria donde se aplica un momento de flexióna una parte giratoria. Esto se denomina tensión de flexión cíclica y la elevación aérea anterior es un buen ejemplo. Sin embargo, también existen tensiones axiales cíclicas y tensiones torsionales cíclicas . Un ejemplo de tensión axial cíclica sería una cuerda de bungee (ver salto de bungee ), que debe soportar la masa de las personas cuando saltan de estructuras como puentes. Cuando una persona llega al final de un cable, el cable se desvía elásticamentey detiene el descenso de la persona. Esto crea una gran tensión axial en el cordón. Una fracción de la energía potencial elástica almacenada en el cordón se transfiere típicamente a la persona, lanzando a la persona hacia arriba una fracción de la distancia que cayó. La persona vuelve a caer sobre el cable, lo que induce tensión en el cable. Esto sucede varias veces por salto. El mismo cable se usa para varios saltos, lo que crea tensiones cíclicas en el cable que, eventualmente, podrían causar fallas si no se reemplazan.

Tensión cíclica y fallo del material [ editar ]

Cuando se aplican tensiones cíclicas a un material, aunque las tensiones no causan deformación plástica , el material puede fallar debido a la fatiga . La falla por fatiga se modela típicamente descomponiendo los esfuerzos cíclicos en componentes medios y alternos. El estrés medio es el tiempo promedio del estrés principal. La definición de tensión alterna varía entre las diferentes fuentes. Se define como la diferencia entre la tensión mínima y la máxima, o la diferencia entre la tensión media y la máxima. ^{[1] [2] Los} ingenieros intentan diseñar mecanismos cuyas partes están sujetas a un solo tipo (flexión, axial o torsional) de estrés cíclico porque esto se ajusta más a los experimentos utilizados para caracterizar la falla por fatiga en diferentes materiales.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Componentes del cilindro o tensión circunferencial .

En mecánica , una tensión de cilindro es una distribución de tensióncon simetría rotacional ; es decir, que permanece sin cambios si el objeto estresado gira alrededor de algún eje fijo.

Los patrones de tensión del cilindro incluyen:

• Tensión circunferencial o tensión de aro , una tensión normal en la dirección tangencial ( azimut );
• Tensión axial , una tensión normal paralela al eje de simetría cilíndrica;
• Tensión radial , una tensión en direcciones coplanares pero perpendicular al eje de simetría.

El ejemplo clásico (y homónimo) de la tensión del aro es la tensiónaplicada a las bandas de hierro, o aros, de un barril de madera . En una tubería recta y cerrada , cualquier fuerza aplicada a la pared cilíndrica de la tubería por un diferencial de presión dará lugar finalmente a tensiones en el aro. De manera similar, si esta tubería tiene tapas de extremo planas, cualquier fuerza aplicada por la presión estática inducirá una tensión axial perpendicular en la misma pared de la tubería. Las secciones delgadas a menudo tienen una tensión radial insignificante , pero los modelos precisos de carcasas cilíndricas de paredes más gruesas requieren que se tengan en cuenta dichas tensiones.

Definiciones [ editar ]

Aro de estrés [ editar ]

La tensión del aro es la fuerza ejercida circunferencialmente (perpendicular tanto al eje como al radio del objeto) en ambas direcciones sobre cada partícula en la pared del cilindro. Puede ser descrito como:

$${\ displaystyle \ sigma _ {\ theta} = {\ dfrac {F} {tl}} \}

dónde:

• F es la fuerza ejercida circunferencialmente en un área de la pared del cilindro que tiene las siguientes dos longitudes como lados:
• t es el espesor radial del cilindro
• l es la longitud axial del cilindro

Una alternativa al esfuerzo de aro en la descripción de la tensión circunferencial es la tensión de la pared o la tensión de la pared ( T ), que generalmente se define como la fuerza circunferencial total ejercida a lo largo de todo el espesor radial: ^[1]

$${\ displaystyle T = {\ dfrac {F} {l}} \}

Coordenadas cilíndricas

Junto con la tensión axial y la tensión radial , la tensión circunferencial es un componente del tensor de tensión en las coordenadas cilíndricas .

Por lo general, es útil para descomponer cualquier fuerza aplicada a un objeto con simetría de rotación en componentes paralelos a la cilíndrica coordenadas r , z , y θ . Estos componentes de fuerza inducen esfuerzos correspondientes: esfuerzo radial, esfuerzo axial y esfuerzo de aro, respectivamente.

Relación con la presión interna [ editar ]

Suposición de paredes delgadas [ editar ]

Para que la suposición de paredes delgadas sea válida, el recipiente debe tener un espesor de pared de no más de aproximadamente una décima parte (a menudo citado como Diámetro / t> 20) de su radio. ^[2] Esto permite tratar la pared como una superficie y, posteriormente, usar la ecuación de Young-Laplace para estimar la tensión del aro creada por una presión interna en un recipiente de presión cilíndrico de pared delgada:

$${\ displaystyle \ sigma _ {\ theta} = {\ dfrac {Pr} {t}} \} (para un cilindro)

$${\ displaystyle \ sigma _ {\ theta} = {\ dfrac {Pr} {2t}} \} (para una esfera)

dónde

• P es la presión interna
• t es el espesor de la pared
• r es el radio medio del cilindro.
• $${\ displaystyle \ sigma _ {\ theta} \!} Es el estrés del aro.

La ecuación de esfuerzo de aro para conchas delgadas también es aproximadamente válida para los vasos esféricos, incluidas las células vegetales y las bacterias en las que la presión interna de la turgencia puede alcanzar varias atmósferas. En aplicaciones prácticas de ingeniería para cilindros (tuberías y tubos), la tensión del aro a menudo se reorganiza para la presión, y se llama fórmula de Barlow .

Las unidades del sistema (IPS) pulgada-libra-segundo para P son la fuerza en libras por pulgada cuadrada (psi). Las unidades para t y d son pulgadas (in). Las unidades SI para P son pascales (Pa), mientras que t y d = 2 restán en metros (m).

Cuando el recipiente tiene extremos cerrados, la presión interna actúa sobre ellos para desarrollar una fuerza a lo largo del eje del cilindro. Esto se conoce como la tensión axial y generalmente es menor que la tensión del aro.

$${\ displaystyle \ sigma _ {z} = {\ dfrac {F} {A}} = {\ dfrac {Pd ^ {2}} {(d + 2t) ^ {2} -d ^ {2}}} \ }

Aunque esto puede ser aproximado a

$${\ displaystyle \ sigma _ {z} = {\ dfrac {Pr} {2t}} \}

También en esta situación una tensión radial. $${\ displaystyle \ sigma _ {r} \} está desarrollado y puede estimarse en cilindros de paredes delgadas como:

$${\ displaystyle \ sigma _ {r} = {\ dfrac {-P} {2}} \}

Vasos de paredes gruesas [ editar ]

Cuando el cilindro a estudiar tenga una $${\ displaystyle radio / espesor} relación de menos de 10 (a menudo citada como {\ displaystyle diámetro / espesor <20 font="">) las ecuaciones de los cilindros de paredes delgadas ya no se mantienen, ya que las tensiones varían significativamente entre las superficies internas y externas y ya no se puede ignorar la tensión de corte a través de la sección transversal.

Estas tensiones y tensiones pueden calcularse utilizando las ecuaciones de Lamé , un conjunto de ecuaciones desarrolladas por el matemático francés Gabriel Lamé .

$${\ displaystyle \ sigma _ {r} = A - {\ dfrac {B} {r ^ {2}}} \}

$${\ displaystyle \ sigma _ {\ theta} = A + {\ dfrac {B} {r ^ {2}}} \}

dónde:

$${\ displaystyle A} y $${\ displaystyle B} Son constantes de integración, que pueden descubrirse a partir de las condiciones de contorno.

$${\ displaystyle r} es el radio en el punto de interés (por ejemplo, en las paredes internas o externas)

$${\ displaystyle A} y $${\ displaystyle B}Se puede encontrar por inspección de las condiciones de contorno. Por ejemplo, el caso más simple es un cilindro sólido:

Si $${\ displaystyle R_ {i} = 0} entonces $${\ displaystyle B = 0} y un cilindro sólido no puede tener una presión interna tan $${\ displaystyle A = P_ {o}}

Efectos prácticos [ editar ]

Ingeniería [ editar ]

La fractura se rige por la tensión del aro en ausencia de otras cargas externas, ya que es la mayor tensión principal. Tenga en cuenta que un aro experimenta la mayor tensión en su interior (el exterior y el interior experimentan la misma tensión total que, sin embargo, se distribuye en diferentes circunferencias), por lo que las grietas en las tuberías deberían comenzar desde el interior de la tubería. Esta es la razón por la cual las inspecciones de tuberías después de los terremotos generalmente involucran el envío de una cámara dentro de una tubería para inspeccionar si hay grietas. El rendimiento se rige por una tensión equivalente que incluye la tensión del aro y la tensión longitudinal o radial cuando está ausente.

Medicina [ editar ]

En la patología de las paredes vasculares o gastrointestinales , la tensión de la pared representa la tensión muscular en la pared del vaso. Como resultado de la Ley de Laplace , si se forma un aneurisma en la pared de un vaso sanguíneo, el radio del vaso ha aumentado. Esto significa que la fuerza hacia dentro del vaso disminuye, y por lo tanto el aneurisma continuará expandiéndose hasta que se rompa. Una lógica similar se aplica a la formación de divertículos en el intestino . ^[3]

El desarrollo histórico de la teoría [ editar ]

Pilar de hierro fundido del puente ferroviario de Chepstow , 1852. Los aros de hierro forjado unidos por pasadores (más fuertes en tensión que los de hierro fundido) resisten las tensiones del aro. ^[4]

El primer análisis teórico del estrés en cilindros fue desarrollado por el ingeniero William Fairbairn , a mediados del siglo XIX , asistido por su analista matemático Eaton Hodgkinson . Su primer interés fue estudiar el diseño y los fallos de las calderas de vapor . ^[5] Fairbairn se dio cuenta de que el esfuerzo del aro era el doble del esfuerzo longitudinal, un factor importante en el ensamblaje de las calderas de las hojas enrolladas unidas por remachado . Trabajos posteriores se aplicaron a la construcción de puentes, y la invención de la viga de la caja . En el puente ferroviario de Chepstow , los pilares de hierro fundido están reforzados por bandas externas dehierro forjado . La fuerza longitudinal vertical es una fuerza de compresión que el hierro fundido puede resistir. La tensión del aro es de tracción y, por lo tanto, se agrega hierro forjado, un material con mejor resistencia a la tracción que el hierro fundido.