MECÁNICA

fuerza centrípeta (del latín centrum , "center" y petere , "buscar" ^[1] ) es una fuerza que hace que un cuerpo siga un camino curvo. Su dirección es siempre ortogonal al movimiento del cuerpo y hacia el punto fijo del centro instantáneo de curvatura del camino. Isaac Newton lo describió como "una fuerza por la cual los cuerpos son estirados o impulsados, o de alguna manera tienden, hacia un punto como a un centro". ^[2] En la mecánica newtoniana, la gravedad proporciona la fuerza centrípeta responsable de las órbitas astronómicas.

Un ejemplo común que involucra la fuerza centrípeta es el caso en el que un cuerpo se mueve con una velocidad uniforme a lo largo de una trayectoria circular. La fuerza centrípeta se dirige en ángulo recto al movimiento y también a lo largo del radio hacia el centro de la trayectoria circular. ^[3] [4] La descripción matemática fue derivada en 1659 por el físico holandés Christiaan Huygens .

Fórmula [ editar ]

La magnitud de la fuerza centrípeta sobre un objeto de masa m que se mueve a velocidad tangencial v a lo largo de una trayectoria con radio de curvatura r es: ^[6]

$${\ displaystyle F = ma_ {c} = {\ frac {mv ^ {2}} {r}}}

dónde $${\ displaystyle a_ {c}}Es la aceleración centrípeta . La dirección de la fuerza es hacia el centro del círculo en el que se mueve el objeto, o el círculo oscilante (el círculo que mejor se adapta a la trayectoria local del objeto, si la trayectoria no es circular). ^[7] La velocidad en la fórmula es cuadrada, por lo que dos veces la velocidad necesita cuatro veces la fuerza. La relación inversa con el radio de curvatura muestra que la mitad de la distancia radial requiere el doble de la fuerza. Esta fuerza también se escribe a veces en términos de la velocidad angular ω del objeto alrededor del centro del círculo, relacionada con la velocidad tangencial por la fórmula

$${\ displaystyle v = \ omega r}

así que eso

$${\ displaystyle F = mr \ omega ^ {2} \ ,.}

Expresado usando el período orbital T para una revolución del círculo,

$${\ displaystyle \ omega = {\ frac {2 \ pi} {T}} \,}

la ecuación se convierte

$${\ displaystyle F = mr \ left ({\ frac {2 \ pi} {T}} \ right) ^ {2}.}^[8]

En los aceleradores de partículas, la velocidad puede ser muy alta (cercana a la velocidad de la luz en el vacío), por lo que la misma masa en reposo ahora ejerce una mayor inercia (masa relativista), lo que requiere una mayor fuerza para la misma aceleración centrípeta, por lo que la ecuación se convierte en:

$${\ displaystyle F = {\ frac {\ gamma mv ^ {2}} {r}}}

dónde

$${\ displaystyle \ gamma = {\ frac {1} {\ sqrt {1-v ^ {2} / c ^ {2}}}}}

Se llama el factor de Lorentz .

Más intuitivamente:

$${\ displaystyle F = \ gamma mv \ omega}

que es la tasa de cambio del impulso relativista ($${\ displaystyle \ gamma mv})

Fuentes [ editar ]

Un cuerpo que experimenta un movimiento circular uniforme requiere una fuerza centrípeta, hacia el eje como se muestra, para mantener su trayectoria circular.

En el caso de un objeto que gira alrededor del extremo de una cuerda en un plano horizontal, la fuerza centrípeta sobre el objeto es suministrada por la tensión de la cuerda. El ejemplo de la cuerda es un ejemplo que involucra una fuerza de "tracción". La fuerza centrípeta también puede suministrarse como una fuerza de "empuje", como en el caso de que la reacción normal de una pared suministre la fuerza centrípeta para un jinete de la pared de la muerte .

La idea de Newton de una fuerza centrípeta corresponde a lo que hoy en día se denomina fuerza central . Cuando un satélite está en órbitaalrededor de un planeta , la gravedad se considera una fuerza centrípeta, aunque en el caso de órbitas excéntricas, la fuerza gravitacional se dirige hacia el foco y no hacia el centro instantáneo de curvatura. ^[9]

Otro ejemplo de fuerza centrípeta surge en la hélice que se rastrea cuando una partícula cargada se mueve en un campo magnéticouniforme en ausencia de otras fuerzas externas. En este caso, la fuerza magnética es la fuerza centrípeta que actúa hacia el eje helicoidal.

Análisis de varios casos [ editar ]

A continuación se presentan tres ejemplos de complejidad creciente, con derivaciones de las fórmulas que gobiernan la velocidad y la aceleración.

Movimiento circular uniforme [ editar ]

Ver también: movimiento circular uniforme.

El movimiento circular uniforme se refiere al caso de velocidad constante de rotación. Aquí hay dos enfoques para describir este caso.

Cálculo derivación [ editar ]

En dos dimensiones, el vector de posición. $${\ displaystyle {\ textbf {r}}}, que tiene magnitud (longitud) $${\ displaystyle r} y dirigido en un ángulo $${\ displaystyle \ theta}sobre el eje x, se puede expresar en coordenadas cartesianas usando los vectores unitarios $${\ displaystyle {\ hat {x}}} y $${\ displaystyle {\ hat {y}}}: ^[10]

$${\ displaystyle {\ textbf {r}} = r \ cos (\ theta) {\ hat {x}} + r \ sin (\ theta) {\ hat {y}}.

Supongamos un movimiento circular uniforme , que requiere tres cosas.

1. El objeto se mueve sólo en un círculo.
2. El radio del circulo $${\ displaystyle r} No cambia a tiempo.
3. El objeto se mueve con velocidad angular constante. $${\ displaystyle \ omega}alrededor del circulo Por lo tanto,$${\ displaystyle \ theta = \ omega t} dónde $${\ displaystyle t}es hora.

Ahora encuentra la velocidad $${\ displaystyle {\ textbf {v}}}y aceleración $${\ displaystyle {\ textbf {a}}} de la moción tomando derivados de posición con respecto al tiempo.

$${\ displaystyle {\ textbf {r}} = r \ cos (\ omega t) {\ hat {x}} + r \ sin (\ omega t) {\ hat {y}}}

$${\ displaystyle {\ dot {\ textbf {r}}} = {\ textbf {v}} = - r \ omega \ sin (\ omega t) {\ hat {x}} + r \ omega \ cos (\ omega t) {\ hat {y}}}

$${\ displaystyle {\ ddot {\ textbf {r}}} = {\ textbf {a}} = - r \ omega ^ {2} \ cos (\ omega t) {\ hat {x}} - r \ omega ^ {2} \ sin (\ omega t) {\ hat {y}}}

$${\ displaystyle {\ textbf {a}} = - \ omega ^ {2} (r \ cos (\ omega t) {\ hat {x}} + r \ sin (\ omega t) {\ hat {y}} )}

Observe que el término entre paréntesis es la expresión original de $${\ displaystyle {\ textbf {r}}}En coordenadas cartesianas . Por consiguiente,

$${\ displaystyle {\ textbf {a}} = - \ omega ^ {2} {\ textbf {r}}.

lo negativo muestra que la aceleración apunta hacia el centro del círculo (opuesto al radio), por lo que se llama "centrípeta" (es decir, "búsqueda del centro"). Mientras que los objetos siguen naturalmente una trayectoria recta (debido a la inercia ), esta aceleración centrípeta describe la trayectoria de movimiento circular causada por una fuerza centrípeta.

Derivación utilizando vectores [ editar ]

Esta sección no cita ninguna fuente . Por favor, ayuda a mejorar esta sección mediante la adición de citas de fuentes confiables . El material sin fuente puede ser desafiado y eliminado . ( Junio ​​de 2009 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

Relaciones vectoriales para movimiento circular uniforme; el vector Ω que representa la rotación es normal al plano de la órbita con la polaridad determinada por la regla de la mano derecha y la magnitud dθ / dt .

La imagen de la derecha muestra las relaciones vectoriales para un movimiento circular uniforme. La rotación en sí misma está representada por el vector de velocidad angular Ω , que es normal al plano de la órbita (usando la regla de la mano derecha ) y tiene una magnitud dada por:

$${\ displaystyle | \ mathbf {\ Omega} | = {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} = \ omega \,}

con θ la posición angular en el tiempo t . En esta subsección, d θ / d t se supone constante, independientemente del tiempo. La distancia recorrida dℓ de la partícula en el tiempo d t a lo largo de la trayectoria circular es

$${\ displaystyle \ mathrm {d} {\ boldsymbol {\ ell}} = \ mathbf {\ Omega} \ times \ mathbf {r} (t) \ mathrm {d} t \,}

el cual, por las propiedades del producto cruzado vectorial , tiene una magnitud r d θ y está en la dirección tangente a la trayectoria circular.

Por consiguiente,

$${\ displaystyle {\ frac {\ mathrm {d} \ mathbf {r}} {\ mathrm {d} t}} = \ lim _ {{\ Delta} t \ to 0} {\ frac {\ mathbf {r} (t + {\ Delta} t) - \ mathbf {r} (t)} {{\ Delta} t}} = {\ frac {\ mathrm {d} {\ boldsymbol {\ ell}}} {\ mathrm {d } t}} \.}

En otras palabras,

$${\ displaystyle \ mathbf {v} \ {\ stackrel {\ mathrm {def}} {=}} \ {\ frac {\ mathrm {d} \ mathbf {r}} {\ mathrm {d} t}} = { \ frac {\ mathrm {d} \ mathbf {\ boldsymbol {\ ell}}} {\ mathrm {d} t}} = \ mathbf {\ Omega} \ times \ mathbf {r} (t) \.}

Diferenciarse con respecto al tiempo,

$${\ displaystyle \ mathbf {a} \ {\ stackrel {\ mathrm {def}} {=}} \ {\ frac {\ mathrm {d} \ mathbf {v}} {d \ mathrm {t}}} = \ mathbf {\ Omega} \ times {\ frac {\ mathrm {d} \ mathbf {r} (t)} {\ mathrm {d} t}} = \ mathbf {\ Omega} \ times \ left [\ mathbf {\ Omega} \ times \ mathbf {r} (t) \ right] \.}

La fórmula de Lagrange dice:

$${\ displaystyle \ mathbf {a} \ times \ left (\ mathbf {b} \ times \ mathbf {c} \ right) = \ mathbf {b} \ left (\ mathbf {a} \ cdot \ mathbf {c} \ derecha) - \ mathbf {c} \ left (\ mathbf {a} \ cdot \ mathbf {b} \ right) \.}

Aplicando la fórmula de Lagrange con la observación de que Ω • r ( t ) = 0 en todo momento,

$${\ displaystyle \ mathbf {a} = - {| \ mathbf {\ Omega |}} ^ {2} \ mathbf {r} (t) \.}

En palabras, la aceleración apunta directamente en dirección opuesta al desplazamiento radial r en todo momento, y tiene una magnitud:

$${\ displaystyle | \ mathbf {a} | = | \ mathbf {r} (t) | \ left ({\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} \ right) ^ { 2} = r {\ omega} ^ {2} \}

donde barras verticales | ... | denota la magnitud del vector, que en el caso de r ( t ) es simplemente el radio r de la trayectoria. Este resultado concuerda con la sección anterior, aunque la notación es ligeramente diferente.

Cuando la velocidad de rotación se hace constante en el análisis del movimiento circular no uniforme , ese análisis concuerda con este.

Un mérito del enfoque vectorial es que es manifiestamente independiente de cualquier sistema de coordenadas.

Ejemplo: El giro bancado [ editar ]

Artículo principal: Giro bancario.

Ver también: Fuerza centrífuga reactiva.

Panel superior: Bola en una pista circular agrupada que se mueve con velocidad constante v ; Panel inferior: Fuerzas sobre el balón.

El panel superior de la imagen de la derecha muestra una bola en movimiento circular en una curva agrupada. La curva se deposita en un ángulo θ de la horizontal, y la superficie de la carretera se considera que es resbaladiza. El objetivo es encontrar qué ángulo debe tener el banco para que la bola no se salga de la carretera. ^{[11] La} intuición nos dice que, en una curva plana sin banca, la bola simplemente se deslizará fuera de la carretera; mientras que con una banca muy empinada, la bola se deslizará hacia el centro a menos que viaje la curva rápidamente.

Aparte de cualquier aceleración que pueda ocurrir en la dirección de la ruta, el panel inferior de la imagen de arriba indica las fuerzas sobre la bola. Hay dos fuerzas; una es la fuerza de gravedad verticalmente hacia abajo a través del centro de masa de la bola m g , donde m es la masa de la bola yg es la aceleración gravitacional ; el segundo es la fuerza normal ascendente ejercida por la carretera en ángulo recto con respecto a la superficie de la carretera m a _n . La fuerza centrípeta exigida por el movimiento curvo también se muestra arriba. Esta fuerza centrípeta no es una tercera fuerza aplicada a la pelota, sino que debe ser proporcionada por la fuerza netaen la bola resultante de la adición vectorial de la fuerza normal y la fuerza de la gravedad . La fuerza resultante o neta sobre la bola encontrada por la adición vectorial de la fuerza normalejercida por la carretera y la fuerza vertical debida a la gravedad debe ser igual a la fuerza centrípeta dictada por la necesidad de recorrer una trayectoria circular. El movimiento curvo se mantiene siempre que esta fuerza neta proporcione el requisito de fuerza centrípeta para el movimiento.

La fuerza neta horizontal sobre la bola es el componente horizontal de la fuerza de la carretera, que tiene magnitud | F _h | = m | un _n | pecado θ . La componente vertical de la fuerza de la carretera debe contrarrestar la fuerza gravitacional: | F _v | = m | a _n | cos θ = m | g |, lo que implica | a _n | = | g | / cos θ . Sustituyendo en la fórmula anterior para | F _h | Se obtiene una fuerza horizontal para ser:

$${\ displaystyle | \ mathbf {F} _ {\ mathrm {h}} | = m | \ mathbf {g} | {\ frac {\ mathrm {sin} \ \ theta} {\ mathrm {cos} \ \ theta} } = m | \ mathbf {g} | \ mathrm {tan} \ \ theta \.}

Por otro lado, a velocidad | v | en una trayectoria circular de radio r , cinemática dice que la fuerza necesaria para girar la bola de forma continua en la vuelta es la radialmente hacia el interior centrípeta fuerza F _c de magnitud:

$${\ displaystyle | \ mathbf {F} _ {\ mathrm {c}} | = m | \ mathbf {a} _ {\ mathrm {c}} | = {\ frac {m | \ mathbf {v} | ^ { 2}} {r}} \.}

En consecuencia, la bola está en una trayectoria estable cuando el ángulo de la carretera está configurado para satisfacer la condición:

$${\ displaystyle m | \ mathbf {g} | \ mathrm {tan} \ \ theta = {\ frac {m | \ mathbf {v} | ^ {2}} {r}} \,}

o,

$${\ displaystyle \ mathrm {tan} \ \ theta = {\ frac {| \ mathbf {v} | ^ {2}} {| \ mathbf {g} | r}} \.}

A medida que el ángulo del banco θ se aproxima a 90 °, la función tangente se aproxima al infinito, permitiendo valores mayores para | v | ² / r . En palabras, esta ecuación indica que para mayores velocidades (más grande | v|), la carretera debe estar más inclinada (un valor mayor para θ ), y para giros más agudos (más pequeña r ) la carretera también debe estar más inclinada, lo que acuerda con intuición. Cuando el angulo θno satisface la condición anterior, la componente horizontal de la fuerza ejercida por la carretera no proporciona la fuerza centrípeta correcta, y se requiere una fuerza de fricción adicional tangencial a la superficie de la carretera para proporcionar la diferencia. Si la fricción no puede hacer esto (es decir, se excede el coeficiente de fricción ), la bola se desliza a un radio diferente donde se puede realizar el equilibrio. ^[12] [13]

Estas ideas también se aplican al vuelo aéreo. Ver el manual del piloto de la FAA. ^[14]

Movimiento circular no uniforme [ editar ]

Ver también: Movimiento circular y Movimiento circular no uniforme.

Esta sección no cita ninguna fuente . Por favor, ayuda a mejorar esta sección mediante la adición de citas de fuentes confiables . El material sin fuente puede ser desafiado y eliminado . ( Junio ​​de 2009 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

Velocidad y aceleración para el movimiento circular no uniforme: el vector de velocidad es tangencial a la órbita, pero el vector de aceleración no es radialmente hacia adentro debido a su componente tangencial a _θ que aumenta la velocidad de rotación: d ω / dt = | a _θ | / R .

Como una generalización del caso de movimiento circular uniforme, supongamos que la velocidad de rotación angular no es constante. La aceleración ahora tiene un componente tangencial, como se muestra en la imagen a la derecha. Este caso se utiliza para demostrar una estrategia de derivación basada en un sistema de coordenadas polares .

Sea r ( t ) un vector que describe la posición de una masa puntual en función del tiempo. Dado que estamos asumiendo un movimiento circular, vamos a r ( t ) = R · u _r , donde R es una constante (el radio del círculo) y u _r es el vector unitario que apunta desde el origen hasta la masa puntual. La dirección de u _r se describe mediante θ , el ángulo entre el eje x y el vector unitario, medido en sentido contrario a las agujas del reloj desde el eje x. El otro vector unitario para coordenadas polares, u _θes perpendicular a u _r y apunta en la dirección de aumentar θ . Estos vectores de unidades polares pueden expresarse en términos de vectores de unidades cartesianas en las direcciones x e y , denotadas como i y j respectivamente: ^[15]

u _r = cos θ i + sin θ j

y

u _θ = -sin θ i + cos θ j .

Uno puede diferenciar para encontrar la velocidad:

$${\ displaystyle \ mathbf {v} = r {\ frac {\ mathrm {d} \ mathbf {u} _ {\ mathrm {r}}} {\ mathrm {d} t}} = r {\ frac {\ mathrm {d}} {\ mathrm {d} t}} \ left (\ mathrm {cos} \ \ theta \ \ mathbf {i} + \ mathrm {sin} \ \ theta \ \ mathbf {j} \ right)}

$${\ displaystyle = r {\ frac {d \ theta} {dt}} \ left (- \ mathrm {sin} \ \ theta \ \ mathbf {i} + \ mathrm {cos} \ \ theta \ \ mathbf {j} \Correcto)\,}

$${\ displaystyle = r {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {\ theta}} \,}

$${\ displaystyle = \ omega r \ mathbf {u} _ {\ mathrm {\ theta}} \,}

donde ω es la velocidad angular d θ / d t .

Este resultado para la velocidad coincide con las expectativas de que la velocidad debe dirigirse tangencialmente al círculo, y que la magnitud de la velocidad debe ser rω . Diferenciando nuevamente, y notando que

$${\ displaystyle {{\ frac {\ mathrm {d} \ mathbf {u} _ {\ mathrm {\ theta}}} {\ mathrm {d} t}} = - {\ frac {\ mathrm {d} \ theta } {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {r}} = - \ omega \ mathbf {u} _ {\ mathrm {r}}} \,}

Encontramos que la aceleración, a es:

$${\ displaystyle \ mathbf {a} = r \ left ({\ frac {\ mathrm {d} \ omega} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {\ theta}} - \ omega ^ {2} \ mathbf {u} _ {\ mathrm {r}} \ right) \.}

Así, los componentes radiales y tangenciales de la aceleración son:

$${\ displaystyle \ mathbf {a} _ {\ mathrm {r}} = - \ omega ^ {2} r \ \ mathbf {u} _ {\ mathrm {r}} = - {\ frac {| \ mathbf {v } | ^ {2}} {r}} \ \ mathbf {u} _ {\ mathrm {r}} \}   y   $${\ displaystyle \ \ mathbf {a} _ {\ mathrm {\ theta}} = r \ {\ frac {\ mathrm {d} \ omega} {\ mathrm {d} t}} \ \ mathbf {u} _ { \ mathrm {\ theta}} = {\ frac {\ mathrm {d} | \ mathbf {v} |} {\ mathrm {d} t}} \ \ mathbf {u} _ {\ mathrm {\ theta}} \ ,}

donde | v | = r ω es la magnitud de la velocidad (la velocidad).

Estas ecuaciones expresan matemáticamente que, en el caso de un objeto que se mueve a lo largo de un camino circular con una velocidad cambiante, la aceleración del cuerpo se puede descomponer en un componente perpendicular que cambia la dirección del movimiento (la aceleración centrípeta), y un paralelo , o componente tangencial , que cambia la velocidad.

Movimiento planar general [ editar ]

Consulte también: Fuerzas generalizadas , Fuerza generalizada , Coordenadas curvilíneas , Coordenadas generalizadas y Coordenadas ortogonales

El vector de posición r , siempre apunta radialmente desde el origen.

Vector de velocidad v , siempre tangente a la trayectoria del movimiento.

El vector de aceleración a no es paralelo al movimiento radial, sino que se desplaza por las aceleraciones angular y de Coriolis, no es tangente a la trayectoria, sino que se desplaza por las aceleraciones centrípeta y radial.

Vectores cinemáticos en coordenadas polares planas. Observe que la configuración no está restringida al espacio 2d, sino a un plano en cualquier dimensión superior.

Los vectores de unidad polar en dos veces t y t + dt para una partícula con trayectoria r ( t ); a la izquierda, los vectores de unidad u _ρ y u _θ en los dos tiempos se mueven para que sus colas se unan, y se muestra que trazan un arco de un círculo de radio de unidad. Su rotación en el tiempo dt es d θ, exactamente el mismo ángulo que la rotación de la trayectoria r ( t ).

Coordenadas polares [ editar ]

Esta sección necesita citas adicionales para su verificación. Por favor, ayudar a mejorar este artículomediante la adición de citas de fuentes confiables . El material sin fuente puede ser desafiado y eliminado.  Encuentre fuentes: "Fuerza centrípeta"  - noticias  ·periódicos  ·libros  ·erudito  ·JSTOR ( junio de 2009 ) (Aprenda cómo y cuándo eliminar este mensaje de plantilla )

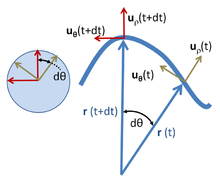
Los resultados anteriores pueden derivarse quizás más simplemente en coordenadas polares , y al mismo tiempo extenderse al movimiento general dentro de un plano, como se muestra a continuación. Las coordenadas polares en el plano emplean un vector de unidad radial u _ρ y un vector de unidad angular u _θ , como se muestra arriba. ^[16] Una partícula en la posición r se describe por:

$${\ displaystyle \ mathbf {r} = \ rho \ mathbf {u} _ {\ rho} \,}

donde se usa la notación ρ para describir la distancia del camino desde el origen en lugar de R para enfatizar que esta distancia no es fija, sino que varía con el tiempo. El vector unitario u _ρ viaja con la partícula y siempre apunta en la misma dirección que r ( t ). El vector unitario u _travel también viaja con la partícula y permanece ortogonal a u _ρ . Por lo tanto, u _ρ y u _θ forman un sistema de coordenadas cartesiano local unido a la partícula, y atado a la trayectoria recorrida por la partícula. ^[17]Al mover los vectores unitarios para que sus colas coincidan, como se ve en el círculo a la izquierda de la imagen de arriba, se ve que u _ρ y u _θ forman un par en ángulo recto con puntas en el círculo unitario que se trazan hacia adelante y hacia atrás el perímetro de este círculo con el mismo ángulo θ ( t ) que r ( t ).

Cuando la partícula se mueve, su velocidad es

$${\ displaystyle \ mathbf {v} = {\ frac {\ mathrm {d} \ rho} {\ mathrm {d} t}} \ mathbf {u} _ {\ rho} + \ rho {\ frac {\ mathrm { d} \ mathbf {u} _ {\ rho}} {\ mathrm {d} t}} \.}

Para evaluar la velocidad, se necesita la derivada del vector unitario u _ρ . Debido a que u _ρ es un vector unitario, su magnitud es fija y puede cambiar solo en la dirección, es decir, su cambio d u _ρ tiene un componente solo perpendicular a u _ρ . Cuando la trayectoria r ( t ) gira una cantidad d θ , u _ρ , que apunta en la misma dirección que r ( t ), también gira por d θ . Ver imagen arriba. Por lo tanto, el cambio en u _ρ es

$${\ displaystyle \ mathrm {d} \ mathbf {u} _ {\ rho} = \ mathbf {u} _ {\ theta} \ mathrm {d} \ theta \,}

o

${\displaystyle {\frac {\mathrm {d} \mathbf {u} _{\rho }}{\mathrm {d} t}}=\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\ .}$

De manera similar, se encuentra la tasa de cambio de u _θ . Al igual que con u _ρ , u _θ es un vector unitario y solo puede rotar sin cambiar el tamaño. Para permanecer ortogonal a u _ρ mientras que la trayectoria r ( t ) gira una cantidad d θ , u _θ , que es ortogonal a r ( t ), también gira en d θ . Ver imagen arriba. Por lo tanto, el cambio d u _θes ortogonal a u _θ y proporcional a d θ (vea la imagen de arriba):

$${\ displaystyle {\ frac {\ mathrm {d} \ mathbf {u} _ {\ theta}} {\ mathrm {d} t}} = - {\ frac {\ mathrm {d} \ theta} {\ mathrm { d} t}} \ mathbf {u} _ {\ rho} \.}

La imagen de arriba muestra que el signo es negativo: para mantener la ortogonalidad, si d u _ρ es positivo con d θ , entonces d u _θ debe disminuir.

Sustituyendo la derivada de u _ρ en la expresión por velocidad:

$${\ displaystyle \ mathbf {v} = {\ frac {\ mathrm {d} \ rho} {\ mathrm {d} t}} \ mathbf {u} _ {\ rho} + \ rho \ mathbf {u} _ { \ theta} {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} = v _ {\ rho} \ mathbf {u} _ {\ rho} + v _ {\ theta} \ mathbf {u } _ {\ theta} = \ mathbf {v} _ {\ rho} + \ mathbf {v} _ {\ theta} \.}

Para obtener la aceleración, se realiza otra diferenciación temporal:

$${\ displaystyle \ mathbf {a} = {\ frac {\ mathrm {d} ^ {2} \ rho} {\ mathrm {d} t ^ {2}}} \ mathbf {u} _ {\ rho} + { \ frac {\ mathrm {d} \ rho} {\ mathrm {d} t} {\ frac {\ mathrm {d} \ mathbf {u} _ {\ rho}} {\ mathrm {d} t}} + {\ frac {\ mathrm {d} \ rho} {\ mathrm {d} t}} \ mathbf {u} _ {\ theta} {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t }} + \ rho {\ frac {\ mathrm {d} \ mathbf {u} _ {\ theta}} {\ mathrm {d} t}} {\ frac {\ mathrm {d} \ theta} {\ mathrm { d} t}} + \ rho \ mathbf {u} _ {\ theta} {\ frac {\ mathrm {d} ^ {2} \ theta} {\ mathrm {d} t ^ {2}}} \.}

Sustituyendo los derivados de u _ρ y u _θ , la aceleración de la partícula es: ^[18]

${\displaystyle \mathbf {a} ={\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}\mathbf {u} _{\rho }+2{\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}-\rho \mathbf {u} _{\rho }\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\ ,}$

${\displaystyle =\mathbf {u} _{\rho }\left[{\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}-\rho \left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]+\mathbf {u} _{\theta }\left[2{\frac {\mathrm {d} \rho }{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right]\ }$

$${\ displaystyle = \ mathbf {u} _ {\ rho} \ left [{\ frac {\ mathrm {d} v _ {\ rho}} {\ mathrm {d} t}} - {\ frac {v _ {\ theta } ^ {2}} {\ rho}} \ right] + \ mathbf {u} _ {\ theta} \ left [{\ frac {2} {\ rho}} v _ {\ rho} v _ {\ theta} + \ rho {\ frac {\ mathrm {d}} {\ mathrm {d} t}} {\ frac {v _ {\ theta}} {\ rho}} \ right] \.}

Como ejemplo particular, si la partícula se mueve en un círculo de radio constante R , entonces d ρ / d t = 0, v = v _θ , y:

$${\ displaystyle \ mathbf {a} = \ mathbf {u} _ {\ rho} \ left [- \ rho \ left ({\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} \ derecha) ^ {2} \ derecha] + \ mathbf {u} _ {\ theta} \ izquierda [\ rho {\ frac {\ mathrm {d} ^ {2} \ theta} {\ mathrm {d} t ^ { 2}}} \ right] \}

$${\ displaystyle = \ mathbf {u} _ {\ rho} \ left [- {\ frac {v ^ {2}} {r}} \ right] + \ mathbf {u} _ {\ theta} \ left [{ \ frac {\ mathrm {d} v} {\ mathrm {d} t}} \ right] \}

dónde $${\ displaystyle v = v _ {\ theta}.}

Estos resultados concuerdan con los anteriores para el movimiento circular no uniforme . Véase también el artículo sobre el movimiento circular no uniforme . Si esta aceleración se multiplica por la masa de partículas, el término principal es la fuerza centrípeta y el negativo del segundo término relacionado con la aceleración angular a veces se denomina fuerza de Euler . ^[19]

Para trayectorias distintas del movimiento circular, por ejemplo, la trayectoria más general prevista en la imagen de arriba, el centro instantáneo de rotación y el radio de curvatura de la trayectoria se relacionan solo de manera indirecta con el sistema de coordenadas definido por u _ρ y u _θ y con la longitud | r ( t ) | = ρ . En consecuencia, en el caso general, no es sencillo separar los términos centrípeto y Euler de la ecuación de aceleración general anterior. ^[20] [21] Para tratar directamente este problema, las coordenadas locales son preferibles, como se explica a continuación.

Coordenadas locales [ editar ]

Sistema de coordenadas local para el movimiento planar en una curva. Se muestran dos posiciones diferentes para las distancias s y s + ds a lo largo de la curva. En cada posición s , el vector unitario u _n apunta a lo largo de la curva hacia afuera y el vector unitario u _t es tangencial a la trayectoria. El radio de curvatura de la trayectoria es ρ según se encuentra a partir de la velocidad de rotación de la tangente a la curva con respecto a la longitud del arco, y es el radio del círculo de oscilación en la posición s . El círculo unitario de la izquierda muestra la rotación de los vectores unitarios con s .

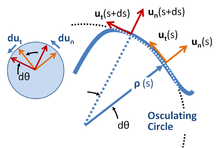
Las coordenadas locales significan un conjunto de coordenadas que viajan con la partícula, ^[22] y tienen una orientación determinada por la trayectoria de la partícula. ^[23] Los vectores unitarios se forman como se muestra en la imagen de la derecha, tanto tangencial como normal a la trayectoria. Este sistema de coordenadas a veces se denomina coordenadas intrínsecas o de trayectoria ^[24] [25] o coordenadas nt , para tangencial normal , en referencia a estos vectores unitarios. Estas coordenadas son un ejemplo muy especial de un concepto más general de coordenadas locales de la teoría de formas diferenciales. ^[26]

La distancia a lo largo de la trayectoria de la partícula es la longitud del arco s , considerada como una función conocida del tiempo.

$${\ displaystyle s = s (t) \.}

Un centro de curvatura se define en cada posición s ubicada a una distancia ρ (el radio de curvatura ) de la curva en una línea a lo largo de la u _n ( s ) normal . La distancia requerida ρ ( s ) en la longitud del arco sse define en términos de la velocidad de rotación de la tangente a la curva, que a su vez está determinada por la propia trayectoria. Si la orientación de la tangente en relación con alguna posición de inicio es θ ( s ), entonces ρ ( s ) se define mediante la derivada d θ / d s :

$${\ displaystyle {\ frac {1} {\ rho (s)}} = \ kappa (s) = {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} s}} \.}

El radio de curvatura generalmente se toma como positivo (es decir, como un valor absoluto), mientras que la curvatura κ es una cantidad con signo.

Un enfoque geométrico para encontrar el centro de curvatura y el radio de curvatura usa un proceso limitante que conduce al círculo oscilante . ^[27] [28] Ver imagen arriba.

Usando estas coordenadas, el movimiento a lo largo del camino se ve como una sucesión de caminos circulares de centro siempre cambiante, y en cada posición s constituye un movimiento circular no uniforme en esa posición con radio ρ . El valor local de la velocidad de rotación angular viene dado por:

$${\ displaystyle \ omega (s) = {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} = {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} s }} {\ frac {\ mathrm {d} s} {\ mathrm {d} t}} = {\ frac {1} {\ rho (s)}} \ {\ frac {\ mathrm {d} s} { \ mathrm {d} t}} = {\ frac {v (s)} {\ rho (s)}} \,}

con la velocidad local v dada por:

$${\ displaystyle v (s) = {\ frac {\ mathrm {d} s} {\ mathrm {d} t}} \.}

En cuanto a los otros ejemplos anteriores, como los vectores unitarios no pueden cambiar la magnitud, su tasa de cambio es siempre perpendicular a su dirección (consulte el inserto de la izquierda en la imagen de arriba): ^[29]

$${\ displaystyle {\ frac {d \ mathbf {u} _ {\ mathrm {n}} (s)} {ds}} = \ mathbf {u} _ {\ mathrm {t}} (s) {\ frac { d \ theta} {ds}} = \ mathbf {u} _ {\ mathrm {t}} (s) {\ frac {1} {\ rho}} \;} $${\ displaystyle {\ frac {d \ mathbf {u} _ {\ mathrm {t}} (s)} {\ mathrm {d} s}} = - \ mathbf {u} _ {\ mathrm {n}} ( s) {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} s}} = - \ mathbf {u} _ {\ mathrm {n}} (s) {\ frac {1} {\ rho }} \.}

En consecuencia, la velocidad y la aceleración son: ^{[28] [30] [31]}

$${\ displaystyle \ mathbf {v} (t) = v \ mathbf {u} _ {\ mathrm {t}} (s) \;}

y usando la regla de la cadena de diferenciación :

$${\ displaystyle \ mathbf {a} (t) = {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {t}} (s) - { \ frac {v ^ {2}} {\ rho}} \ mathbf {u} _ {\ mathrm {n}} (s) \;} con la aceleración tangencial $${\ displaystyle {\ frac {\ mathrm {\ mathrm {d}} v} {\ mathrm {\ mathrm {d}} t}} = {\ frac {\ mathrm {d} v} {\ mathrm {d} s }} \ {\ frac {\ mathrm {d} s} {\ mathrm {d} t}} = {\ frac {\ mathrm {d} v} {\ mathrm {d} s}} \ v \.}

En este sistema de coordenadas locales, la aceleración se asemeja a la expresión del movimiento circular no uniforme con el radio local ρ ( s ), y la aceleración centrípeta se identifica como el segundo término. ^[32]

La extensión de este enfoque a las curvas espaciales tridimensionales conduce a las fórmulas de Frenet-Serret . ^[33] [34]

Enfoque alternativo [ editar ]

Al observar la imagen de arriba, uno podría preguntarse si se ha tenido en cuenta adecuadamente la diferencia de curvatura entre ρ ( s ) y ρ ( s + d s ) al calcular la longitud del arco como d s = ρ ( s ) d θ . La tranquilidad en este punto se puede encontrar utilizando un enfoque más formal descrito a continuación. Este enfoque también hace conexión con el artículo sobre curvatura .

Para introducir los vectores unitarios del sistema de coordenadas local, una aproximación es comenzar en coordenadas cartesianas y describir las coordenadas locales en términos de estas coordenadas cartesianas. En términos de longitud de arco s , describa la trayectoria como: ^[35]

$${\ displaystyle \ mathbf {r} (s) = \ left [x (s), \ y (s) \ right] \.}

Luego, un desplazamiento incremental a lo largo del camino d s se describe por:

$${\ displaystyle \ mathrm {d} \ mathbf {r} (s) = \ left [\ mathrm {d} x (s), \ \ mathrm {d} y (s) \ right] = \ left [x '( s), \ y '(s) \ right] \ mathrm {d} s \,}

donde se introducen números primos para denotar derivados con respecto a s . La magnitud de este desplazamiento es d s , lo que demuestra que: ^[36]

$${\ displaystyle \ left [x '(s) ^ {2} + y' (s) ^ {2} \ right] = 1 \.} (Ec. 1)

Este desplazamiento es necesariamente una tangente a la curva en s , que muestra que el vector unitario tangente a la curva es:

$${\ displaystyle \ mathbf {u} _ {\ mathrm {t}} (s) = \ left [x '(s), \ y' (s) \ right] \,}

mientras que el vector unitario exterior normal a la curva es

$${\ displaystyle \ mathbf {u} _ {\ mathrm {n}} (s) = \ left [y '(s), \ -x' (s) \ right] \,}

La ortogonalidad se puede verificar mostrando que el producto de punto vectorial es cero. La magnitud unitaria de estos vectores es una consecuencia de la ecuación. 1 . Usando el vector tangente, el ángulo θ de la tangente a la curva está dado por:

$${\ displaystyle \ sin \ theta = {\ frac {y '(s)} {\ sqrt {x' (s) ^ {2} + y '(s) ^ {2}}}} = y' (s) \;} y $${\ displaystyle \ cos \ theta = {\ frac {x '(s)} {\ sqrt {x' (s) ^ {2} + y '(s) ^ {2}}}} = x' (s) \.}

El radio de curvatura se introduce de manera completamente formal (sin necesidad de interpretación geométrica) como:

$${\ displaystyle {\ frac {1} {\ rho}} = {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} s}} \.}

La derivada de θ se puede encontrar a partir de eso para el pecado θ :

$${\ displaystyle {\ frac {\ mathrm {d} \ sin \ theta} {\ mathrm {d} s}} = \ cos \ theta {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} s }} = {\ frac {1} {\ rho}} \ cos \ theta \ = {\ frac {1} {\ rho}} x '(s) \.}

Ahora:

$${\ displaystyle {\ frac {\ mathrm {d} \ sin \ theta} {\ mathrm {d} s}} = {\ frac {\ mathrm {d}} {\ mathrm {d} s}} {\ frac { y '(s)} {\ sqrt {x' (s) ^ {2} + y '(s) ^ {2}}}}} $${\ displaystyle = {\ frac {y '' (s) x '(s) ^ {2} -y' (s) x '(s) x' '(s)} {\ left (x' (s) ^ {2} + y '(s) ^ {2} \ derecha) ^ {3/2}}} \,}

en el que el denominador es unidad. Con esta fórmula para la derivada del seno, el radio de curvatura se convierte en:

$${\ displaystyle {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} s}} = {\ frac {1} {\ rho}} = y '' (s) x '(s) -y '(s) x' '(s) \} $${\ displaystyle = {\ frac {y '' (s)} {x '(s)}} = - {\ frac {x' '(s)} {y' (s)}} \,}

donde la equivalencia de las formas se deriva de la diferenciación de la ecuación. 1 :

$${\ displaystyle x '(s) x' '(s) + y' (s) y '' (s) = 0 \.}

Con estos resultados, la aceleración se puede encontrar:

$${\ displaystyle \ mathbf {a} (s) = {\ frac {\ mathrm {d}} {\ mathrm {d} t}} \ mathbf {v} (s) ${\displaystyle ={\frac {\mathrm {d} }{\mathrm {d} t}}\left[{\frac {\mathrm {d} s}{\mathrm {d} t}}\left(x'(s),\ y'(s)\right)\right]\ }$

${\displaystyle =\left({\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}\right)\mathbf {u} _{\mathrm {t} }(s)+\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}\left(x''(s),\ y''(s)\right)}$

${\displaystyle =\left({\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}\right)\mathbf {u} _{\mathrm {t} }(s)-\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}{\frac {1}{\rho }}\mathbf {u} _{\mathrm {n} }(s)\ ,}$

como puede verificarse tomando el producto de puntos con los vectores unitarios u _t ( s ) y u _n ( s ). Este resultado para la aceleración es el mismo que para el movimiento circular basado en el radio ρ . Usando este sistema de coordenadas en el marco inercial, es fácil identificar la fuerza normal a la trayectoria como la fuerza centrípeta y paralela a la trayectoria como la fuerza tangencial. Desde un punto de vista cualitativo, la trayectoria se puede aproximar mediante un arco de círculo durante un tiempo limitado, y durante el tiempo limitado en que se aplica un radio de curvatura particular, las fuerzas centrífugas y de Euler se pueden analizar en base al movimiento circular con ese radio .

Este resultado para la aceleración concuerda con el encontrado anteriormente. Sin embargo, en este enfoque, la cuestión del cambio en el radio de curvatura con s se maneja de manera completamente formal, consistente con una interpretación geométrica, pero sin confiar en ella, evitando así cualquier pregunta que la imagen anterior pueda sugerir acerca de descuidar la variación en ρ .

Ejemplo: movimiento circular [ editar ]

Esta sección no cita ninguna fuente . Por favor, ayuda a mejorar esta sección mediante la adición de citas de fuentes confiables . El material sin fuente puede ser desafiado y eliminado . ( Junio ​​de 2009 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

Para ilustrar las fórmulas anteriores, sea x , y se den como:

$${\ displaystyle x = \ alpha \ cos {\ frac {s} {\ alpha}} \; \ y = \ alpha \ sin {\ frac {s} {\ alpha}} \.}

Entonces:

$${\ displaystyle x ^ {2} + y ^ {2} = \ alpha ^ {2} \,}

que puede reconocerse como una trayectoria circular alrededor del origen con un radio α . La posición s = 0 corresponde a [ α , 0] o a las 3 en punto. Para utilizar el formalismo anterior, se necesitan los derivados:

$${\ displaystyle y ^ {\ prime} (s) = \ cos {\ frac {s} {\ alpha}} \; \ x ^ {\ prime} (s) = - \ sin {\ frac {s} {\ alfa}} \,}

$${\ displaystyle y ^ {\ prime \ prime} (s) = - {\ frac {1} {\ alpha}} \ sin {\ frac {s} {\ alpha}} \; \ x ^ {\ prime \ prime } (s) = - {\ frac {1} {\ alpha}} \ cos {\ frac {s} {\ alpha}} \.}

Con estos resultados, se puede verificar que:

$${\ displaystyle x ^ {\ prime} (s) ^ {2} + y ^ {\ prime} (s) ^ {2} = 1 \; \ {\ frac {1} {\ rho}} = y ^ { \ prime \ prime} (s) x ^ {\ prime} (s) -y ^ {\ prime} (s) x ^ {\ prime \ prime} (s) = {\ frac {1} {\ alpha}} \.}

Los vectores unitarios también se pueden encontrar:

$${\ displaystyle \ mathbf {u} _ {\ mathrm {t}} (s) = \ left [- \ sin {\ frac {s} {\ alpha}} \, \ \ cos {\ frac {s} {\ alfa}} \ derecha] \; \ \ mathbf {u} _ {\ mathrm {n}} (s) = izquierda [\ cos {\ frac {s} {\ alpha}} \, \ \ sin {\ frac {s} {\ alpha}} \ right] \,}

que sirven para mostrar que s = 0 está ubicado en la posición [ ρ , 0] y s = ρ π / 2 en [0, ρ ], que concuerda con las expresiones originales para x e y . En otras palabras, s se mide en sentido contrario a las agujas del reloj alrededor del círculo desde las 3 en punto. Además, los derivados de estos vectores se pueden encontrar:

$${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} s}} \ mathbf {u} _ {\ mathrm {t}} (s) = - {\ frac {1} {\ alpha} } \ left [\ cos {\ frac {s} {\ alpha}} \, \ \ sin {\ frac {s} {\ alpha}} \ right] = - {\ frac {1} {\ alpha}} \ mathbf {u} _ {\ mathrm {n}} (s) \;}

$${\ displaystyle \ {\ frac {\ mathrm {d}} {\ mathrm {d} s}} \ mathbf {u} _ {\ mathrm {n}} (s) = {\ frac {1} {\ alpha} } \ left [- \ sin {\ frac {s} {\ alpha}} \, \ \ cos {\ frac {s} {\ alpha}} \ right] = {\ frac {1} {\ alpha}} \ mathbf {u} _ {\ mathrm {t}} (s) \.}

Para obtener velocidad y aceleración, es necesaria una dependencia del tiempo para s . Para el movimiento a la izquierda a velocidad variable v ( t ):

$${\ displaystyle s (t) = \ int _ {0} ^ {t} \ dt ^ {\ prime} \ v (t ^ {\ prime}) \,}

donde v ( t ) es la velocidad y t es el tiempo, y s ( t = 0) = 0. Entonces:

$${\ displaystyle \ mathbf {v} = v (t) \ mathbf {u} _ {\ mathrm {t}} (s) \,}

$${\ displaystyle \ mathbf {a} = {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {t}} (s) + v {\ frac {\ mathrm {d}} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {t}} (s) = {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {t}} (s) -v {\ frac {1} {\ alpha}} \ mathbf {u} _ {\ mathrm {n}} (s) {\ frac {\ mathrm {d} s} {\ mathrm {d} t}}}

$${\ displaystyle \ mathbf {a} = {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {t}} (s) - {\ frac { v ^ {2}} {\ alpha}} \ mathbf {u} _ {\ mathrm {n}} (s) \,}

Donde ya se establece que α = ρ. Esta aceleración es el resultado estándar para un movimiento circular no uniforme .