TRIGONOMETRÍA

FUNCIONES ALGEBRAICAS

Un acorde de un círculo es un segmento de línea recta cuyos puntos finales se encuentran en el círculo. Una línea secante , o simplemente secante , es la extensión de línea infinita de un acorde. Más generalmente, un acorde es un segmento de línea que une dos puntos en cualquier curva, por ejemplo, una elipse . Un acorde que pasa a través del punto central de un círculo es el diámetro del círculo. Cada diámetro es un acorde, pero no todo acorde es un diámetro.

La palabra acorde es del latín chorda que significa cuerda de arco .

El segmento rojo BX es un acorde
(como lo es el segmento de diámetro AB ).

En círculos [ editar ]

Artículo principal: Círculo § Acorde

Entre las propiedades de los acordes de un círculo están las siguientes:

1. Los acordes son equidistantes del centro si y solo si sus longitudes son iguales.
2. Los acordes iguales están subtendidos por ángulos iguales desde el centro del círculo.
3. Un acorde que pasa por el centro de un círculo se llama diámetro y es el acorde más largo.
4. Si las extensiones de línea (líneas secantes) de los acordes AB y CD se intersecan en un punto P, entonces sus longitudes satisfacen AP · PB = CP · PD ( potencia del teorema de un punto ).

En puntos suspensivos [ editar ]

Los puntos medios de un conjunto de acordes paralelos de una elipse son colineales . ^[1]

En trigonometría [ editar ]

Los acordes se utilizaron ampliamente en el desarrollo temprano de la trigonometría . La primera tabla trigonométrica conocida, compilada por Hipparchus , tabuló el valor de la función de acorde por cada 7.5 grados . En el siglo II dC, Ptolomeo de Alejandría compiló una tabla de acordes más extensa en su libro de astronomía , que da el valor del acorde para ángulos que van desde 1/2 grado a 180 grados en incrementos de medio grado. El círculo tenía un diámetro de 120, y las longitudes de los acordes tienen una precisión de dos dígitos de base-60 después de la parte entera. ^[2]

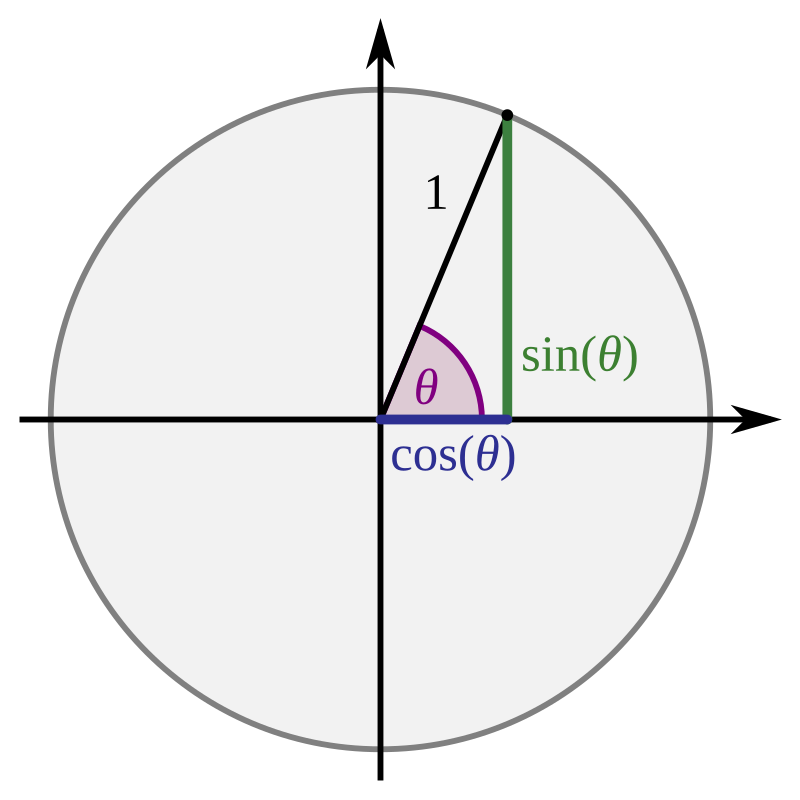
La función de acorde se define geométricamente como se muestra en la imagen. El acorde de un ángulo es la longitud del acorde entre dos puntos en un círculo unitario separado por ese ángulo central. El ángulo θ se toma en el sentido positivo y debe estar en el intervalo de 0 < θ ≤ pi (radianes). La función de acorde puede relacionarse con la función sinusoidal moderna , tomando uno de los puntos para ser (1,0) y el otro punto para ser ( cos θ , sin θ ), y luego usar el teorema de Pitágoras para calcular el acorde longitud: ^[2]

$${\ displaystyle \ mathrm {crd} \ \ theta = {\ sqrt {(1- \ cos \ theta) ^ {2} + \ sin ^ {2} \ theta}} = {\ sqrt {2-2 \ cos \ theta}} = 2 \ sin \ izquierda ({\ frac {\ theta} {2}} \ derecha).}

El último paso utiliza la fórmula de medio ángulo . Así como la trigonometría moderna se basa en la función seno, la trigonometría antigua se construyó en la función de acorde. Se supone que Hipparchus escribió un trabajo de doce volúmenes sobre acordes, todos perdidos ahora, por lo que presumiblemente se sabía mucho sobre ellos. La función de acorde satisface muchas identidades análogas a las modernas bien conocidas:

Nombre	Basado en el seno	Basado en el acorde
pitagórico	$${\ displaystyle \ sin ^ {2} \ theta + \ cos ^ {2} \ theta = 1 \,}	$${\ displaystyle \ mathrm {crd} ^ {2} \ theta + \ mathrm {crd} ^ {2} (\ pi - \ theta) = 4 \,}
Ángulo medio	$${\ displaystyle \ sin {\ frac {\ theta} {2}} = \ pm {\ sqrt {\ frac {1- \ cos \ theta} {2}}} \,}	$${\ displaystyle \ mathrm {crd} \ {\ frac {\ theta} {2}} = \ pm {\ sqrt {2- \ mathrm {crd} (\ pi - \ theta)}} \,}
Apotem ( a )	$${\ displaystyle c = 2 {\ sqrt {r ^ {2} -a ^ {2}}}}	$${\ displaystyle c = {\ sqrt {D ^ {2} -4a ^ {2}}}}
Ángulo ( θ )	$${\ displaystyle c = 2r \ sin \ left ({\ frac {\ theta} {2}} \ right)}	$${\ displaystyle c = {\ frac {D} {2}} \ mathrm {crd} \ \ theta}

La función inversa también existe: ^[3]

$${\ displaystyle \ operatorname {acrd} (y) = 2 \ arcsin \ left ({\ frac {y} {2}} \ right).}

El exsecante ( exsec , exs ) y excosecant ( excosec , excsc , exc ) son funciones trigonométricas definidos en términos de los secantes y cosecant funciones. Que solían ser importantes en campos como la topografía , la ingeniería ferroviaria , la ingeniería civil , la astronomía , y la trigonometría esférica y podría ayudar a mejorar la precisión, pero rara vez se utilizan hoy en día, excepto para simplificar algunos cálculos.

Exsecante [ editar ]

Las funciones trigonométricas, incluyendo el exsecante, se pueden construir geométricamente en términos de una unidad de círculo con centro en O . El exsecante es la porción DE del exterior secante al círculo.

El  exsecante , ^{[2] [3] [4] [5] [6] [7] [8] [9]} (Latín: secans exterior ^{[10] [11] [12] [13]} ) también conocido como exterior , externo , ^{[1] [14] [15] [16] [17]} hacia el exterior o secante exterior y abreviado como exsec ^{[14] [2] [5] [18] [7] [8] [9] [15] [ 16] [19] [20] [21]} o exs , ^[22]es una función trigonométrica definida en términos de la función secante sec ( θ ): ^{[7] [21] [23]}

$${\ displaystyle \ operatorname {exsec} (\ theta) = \ sec (\ theta) -1 = {\ frac {1} {\ cos (\ theta)}} - 1.}^{[7] [8] [9] [15] [16] [19] [20] [21] [23]}

El nombre exsecant se puede entender a partir de una construcción gráfica de las diversas funciones trigonométricas de un círculo unitario , como se usó históricamente. sec ( θ ) es la línea de separación OE , y el exsecante es la parte DE de esta secante que se encuentra en el exterior del círculo (por ejemplo, el latín es el de afuera ).

Excosecante [ editar ]

exsecante (azul) y excosecante (verde)

Una función relacionada es la excosecant ^[5] [24] o coexsecant , ^{[25] [18] [26]}también conocido como exterior , externo , ^[17] hacia el exterior o cosecant exterior y abreviado como excosec , coexsec , ^{[14] [18 ] [26]} excsc ^[5] [24] o exc , ^[22] la exsecante del ángulo complementario:

$${\ displaystyle \ operatorname {excsc} (\ theta) = \ operatorname {exsec} \ left ({\ frac {\ pi} {2}} - \ theta \ right) = \ csc (\ theta) -1 = {\ frac {1} {\ sin (\ theta)}} - 1.}^[24]

Uso [ editar ]

Importante en campos como topografía , ^[8] ingeniería ferroviaria ^[5] (por ejemplo, para trazar curvas de ferrocarril y peralte ), ingeniería civil , astronomía y trigonometría esférica hasta la década de 1980, la función exsecante ahora es poco utilizada. ^[8] [23] Principalmente, esto se debe a que la amplia disponibilidad de calculadoras y computadoras ha eliminado la necesidad de tablas trigonométricas de funciones especializadas como esta. ^[8]

La razón para definir una función especial para el exsecante es similar a la razón de ser de la versión : para ángulos pequeños θ , la función seg ( θ ) se aproxima a una , por lo que usar la fórmula anterior para el exsecante implicará la resta de dos casi iguales cantidades, resultando en la cancelación catastrófica . Por lo tanto, una tabla de la función secante necesitaría una precisión muy alta para ser utilizada por el exsecant, haciendo que una tabla especializada exsecant sea útil. Incluso con una computadora, los errores de punto flotante pueden ser problemáticos para exsecantes de ángulos pequeños, si se usa la definición basada en coseno. Una fórmula más precisa en este límite sería usar la identidad:

$${\ displaystyle \ operatorname {exsec} (\ theta) = {\ frac {1- \ cos (\ theta)} {\ cos (\ theta)}} = {\ frac {\ operatorname {versin} (\ theta)} {\ cos (\ theta)}} = \ operatorname {versin} (\ theta) \ sec (\ theta) = 2 \ left (\ sin \ left ({\ frac {\ theta} {2}} \ right) \ derecha) ^ {2} \ sec (\ theta)}^{[3] [4] [17]}

o

$${\ displaystyle \ operatorname {excsc} (\ theta) = {\ frac {1- \ sin (\ theta)} {\ sin (\ theta)}} = {\ frac {\ operatorname {coversin} (\ theta)} {\ sin (\ theta)}} = \ operatorname {coversin} (\ theta) \ csc (\ theta) = 2 \ left (\ cos \ left ({\ frac {\ theta} {2}} \ right) \ derecha) ^ {2} \ csc (\ theta). \}^[17]

Antes de la disponibilidad de computadoras, esto requeriría multiplicaciones que consumieran mucho tiempo.

La función exsecante fue utilizada por Galileo Galilei en 1632, aunque todavía la llamaba segante (que significa secante ). ^{[27] [28] [29] [30]} El término latino secans exterior se usó desde al menos alrededor de 1745. ^{[10] [11] [12] [13]} El uso del término inglés secant externo y la abreviatura ej. segundo. Se puede remontar a 1855 cuando Charles Haslett publicó la primera tabla de exsecantes conocida . ^[1] [31] Variaciones como ex secante y exsecestaban en uso en 1880, ^[14] y exsecant se utilizó desde 1894 como mínimo. ^[2]

Los términos coexsecante ^[25] y coexsec ^{[2] también} se pueden usar desde 1880 ^[2] [25] seguido de excosecantedesde 1909. ^[5] Albert Einstein también utilizó la función para describir la energía cinética de fermiones . ^[29] [30]

Identidades matemáticas [ editar ]

Derivados [ editar ]

$${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} \ theta}} \ operatorname {exsec} (\ theta) = \ tan (\ theta) \ sec (\ theta) = {\ frac { \ sin (\ theta)} {(\ cos (\ theta)) ^ {2}}}}^[21]

$${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} \ theta}} \ operatorname {excsc} (\ theta) = - \ cot (\ theta) \ csc (\ theta) = {\ frac {- \ cos (\ theta)} {(\ sin (\ theta)) ^ {2}}}}

Integrales [ editar ]

$${\ displaystyle \ int \ operatorname {exsec} (\ theta) \, \ mathrm {d} \ theta = \ ln \ left [\ cos \ left ({\ frac {\ theta} {2}} \ right) + \ sin \ left ({\ frac {\ theta} {2}} \ right) \ right] - \ ln \ left [\ cos \ left ({\ frac {\ theta} {2}} \ right) - \ sin \ izquierda ({\ frac {\ theta} {2}} \ derecha) \ derecha] - \ theta + C}^[21]

$${\ displaystyle \ int \ operatorname {excsc} (\ theta) \, \ mathrm {d} \ theta = \ ln \ left [\ tan \ left ({\ frac {\ theta} {2}} \ right) \ right ] - \ theta + C}

Funciones inversas [ editar ]

Las funciones inversas arcexsecant ^[26] ( arcexsec , ^[5] [26] aexsec , ^[32] [33] aexs , exsec- ¹ ) y arcexcosecant ( arcexcosec , arcexcec , ^[5] aexcsc , aexc , arccoexsecant , arccoexs , cccxexccccc ^{) 1} ) existe también:

$${\ displaystyle \ operatorname {arcexsec} (y) = \ operatorname {arcsec} (y + 1) = \ arccos \ left ({\ frac {1} {y + 1}} \ right) = \ arctan ({\ sqrt {y ^ {2} + 2y}})}^{[26] [32] [33]} (para y  ≤ −2 o y  ≥ 0) ^[26]

$${\ displaystyle \ operatorname {arcexcsc} (y) = \ operatorname {arccsc} (y + 1) = \ arcsin \ left ({\ frac {1} {y + 1}} \ right) \,}

Otras propiedades [ editar ]

Derivado del círculo unitario:

$${\ displaystyle \ operatorname {exsec} (\ theta) = \ sec (\ theta) - \ cos (\ theta) - \ operatorname {versin} (\ theta).}

$${\ displaystyle \ operatorname {excsc} (\ theta) = \ operatorname {csc} (\ theta) - \ sin (\ theta) - \ operatorname {coversin} (\ theta).}

La función exsecant está relacionada con la función tangente por

$${\ displaystyle \ operatorname {exsec} (\ theta) = \ tan (\ theta) \ tan \ left ({\ frac {\ theta} {2}} \ right).}^[23]

En analogía, la función excosecante está relacionada con la función cotangente por

$${\ displaystyle \ operatorname {excsc} (\ theta) = \ cot (\ theta) \ cot \ left ({\ frac {\ theta} {2}} \ right).}

La función exsecant está relacionada con la función seno por

$${\ displaystyle \ operatorname {exsec} (\ theta) = {\ frac {1} {\ sqrt {1 - (\ sin (\ theta)) ^ {2}}}} - 1.}

En analogía, la función excosecante está relacionada con la función coseno por

$${\ displaystyle \ operatorname {excsc} (\ theta) = {\ frac {1} {\ sqrt {1 - (\ cos (\ theta)) ^ {2}}}} - 1.}^[30]

Las funciones exsecant y excosecant se pueden extender al plano complejo . ^[21]

$${\ displaystyle \ lim _ {\ theta \ to 0} {\ frac {\ operatorname {exsec} (\ theta)} {\ theta}} = 0}^[5]

$${\ displaystyle {\ frac {\ operatorname {versin} (\ theta) + \ operatorname {coversin} (\ theta)} {\ operatorname {versin} (\ theta) - \ operatorname {coversin} (\ theta)}} - {\ frac {\ operatorname {exsec} (\ theta) + \ operatorname {excsc} (\ theta)} {\ operatorname {exsec} (\ theta) - \ operatorname {excsc} (\ theta)}} = {\ frac {2 \ operatorname {versin} (\ theta) \ operatorname {coversin} (\ theta)} {\ operatorname {versin} (\ theta) - \ operatorname {coversin} (\ theta)}}}^[5]

$${\ displaystyle (\ operatorname {exsec} (\ theta) + \ operatorname {versin} (\ theta)) \, (\ operatorname {excsc} (\ theta) + \ operatorname {coversin} (\ theta)) = \ sin (\ theta) \ cos (\ theta)}^[5]

$${\ displaystyle \ operatorname {exsec} (2 \ theta) = {\ frac {2 \ sin ^ {2} (\ theta)} {1-2 \ sin ^ {2} (\ theta)}}}^[5]

$${\ displaystyle \ operatorname {exsec} (2 \ theta) \, \ cos (2 \ theta) = \ tan (\ theta)}^[5]

$${\ displaystyle \ operatorname {exsec} ^ {2} (\ theta) +2 \ operatorname {exsec} (\ theta) = \ tan ^ {2} (\ theta)}

Un círculo unitario con funciones trigonométricas .