TRIGONOMETRÍA

FUNCIONES TRIGONOMÉTRICAS - CONTINUACIÓN

Definiciones a través de ecuaciones diferenciales [ editar ]

Tanto la función seno como la coseno satisfacen la ecuación diferencial lineal :

$${\ displaystyle y '' = - y \ ,.}

Es decir, cada uno es el inverso aditivo de su propia segunda derivada. Dentro del espacio de funciónbidimensional V que consiste en todas las soluciones de esta ecuación,

• La función seno es la solución única que satisface la condición inicial. $${\ displaystyle \ left (y '(0), y (0) \ right) = (1,0) \,} y
• La función coseno es la única solución que satisface la condición inicial. $${\ displaystyle \ left (y '(0), y (0) \ right) = (0,1) \,}.

Puesto que las funciones seno y coseno son linealmente independientes, juntos forman una base de V . Este método de definir las funciones seno y coseno es esencialmente equivalente a usar la fórmula de Euler. (Ver ecuación diferencial lineal ). Resulta que esta ecuación diferencial puede usarse no solo para definir las funciones seno y coseno, sino también para probar las identidades trigonométricas de las funciones seno y coseno.

Además, la observación de que el seno y el coseno satisfacen y ″ = - y significa que son funciones propias del operador de la segunda derivada.

La función tangente es la única solución de la ecuación diferencial no lineal.

$${\ displaystyle y '= 1 + y ^ {2} \,}

cumpliendo la condición inicial y (0) = 0 . Hay una prueba visual muy interesante de que la función tangente satisface esta ecuación diferencial. ^[dieciséis]

La importancia de radianes [ editar ]

Los radianes especifican un ángulo midiendo la longitud alrededor de la trayectoria del círculo unitario y constituyen un argumento especial para las funciones seno y coseno. En particular, solo los senos y cosenos que asignan radianes a relaciones satisfacen las ecuaciones diferenciales que los describen clásicamente. Si un argumento para seno o coseno en radianes se escala por frecuencia,

$${\ displaystyle f (x) = \ sin (kx), \,}

entonces los derivados se escalarán por amplitud.

$${\ displaystyle f '(x) = k \ cos (kx). \,}

Aquí, k es una constante que representa un mapeo entre unidades. Si x está en grados, entonces

$${\ displaystyle k = {\ frac {\ pi} {180 ^ {\ circ}}}.}

Esto significa que la segunda derivada de un seno en grados no satisface la ecuación diferencial

$${\ displaystyle y '' = - y \,}

sino mas bien

$${\ displaystyle y '' = - k ^ {2} y. \,}

La segunda derivada del coseno se comporta de manera similar.

Esto significa que estos senos y cosenos son funciones diferentes, y que la cuarta derivada del seno será senoidal nuevamente solo si el argumento está en radianes.

Identidades [ editar ]

Artículos principales: Lista de identidades trigonométricas y Pruebas de identidades trigonométricas.

Muchas identidades interrelacionan las funciones trigonométricas. Entre las más utilizadas se encuentra la identidad de Pitágoras , que establece que para cualquier ángulo, el cuadrado del seno más el cuadrado del coseno es 1. Esto es fácil de ver al estudiar un triángulo rectángulo de hipotenusa 1 y aplicar el teorema de Pitágoras . En forma simbólica, la identidad pitagórica está escrita.

$${\ displaystyle \ sin ^ {2} x + \ cos ^ {2} x = 1}

que es la notación abreviada estándar para

$${\ displaystyle (\ sin x) ^ {2} + (\ cos x) ^ {2} = 1.}

Otras relaciones clave son las fórmulas de suma y diferencia , que dan el seno y el coseno de la suma y la diferencia de dos ángulos en términos de senos y cosenos de los ángulos mismos. Estos pueden derivarse geométricamente, usando argumentos que datan de Ptolomeo . También se pueden producir algebraicamente usando la fórmula de Euler .

Suma

{\ displaystyle {\ begin {alineado} \ sin \ left (x + y \ right) & = \ sin x \ cos y + \ cos x \ sin y, \\\ cos \ left (x + y \ right) & = \ cos x \ cos y- \ sin x \ sin y, \ end {alineado}}}

Diferencia

{\ displaystyle {\ begin {alineado} \ sin \ left (xy \ right) & = \ sin x \ cos y- \ cos x \ sin y, \\\ cos \ left (xy \ right) & = \ cos x \ cos y + \ sin x \ sin y. \ end {alineado}}}

Estos a su vez conducen a las siguientes fórmulas de tres ángulos:

{\ displaystyle {\ begin {alineado} \ sin \ left (x + y + z \ right) & = \ sin x \ cos y \ cos z + \ sin y \ cos z \ cos x + \ sin z \ cos y \ cos x- \ sin x \ sin y \ sin z, \\ cos \ izquierda (x + y + z \ derecha) & = \ cos x \ cos y \ cos z- \ cos x \ sin y \ sin z- \ cos y \ sin x \ sin z- \ cos z \ sin x \ sin y, \ end {alineado}}}

Cuando los dos ángulos son iguales, las fórmulas de suma se reducen a ecuaciones más simples conocidas como fórmulas de doble ángulo .

{\ displaystyle {\ begin {alineado} \ sin \ left (2x \ right) & = 2 \ sin x \ cos x, \\\ cos \ left (2x \ right) & = \ cos ^ {2} x- \ sin ^ {2} x = 2 \ cos ^ {2} x-1 = 1-2 \ sin ^ {2} x. \ end {alineado}}}

Cuando tres ángulos son iguales, las fórmulas de tres ángulos se simplifican para

{\ displaystyle {\ begin {alineado} \ sin (3x) & = 3 \ sin x-4 \ sin ^ {3} x. \\ cos (3x) & = 4 \ cos ^ {3} x-3 \ cos x. \ end {alineado}}}

Estas identidades también se pueden usar para derivar las identidades de producto a suma que se usaron en la antigüedad para transformar el producto de dos números en una suma de números y operaciones de gran velocidad, como la función logarítmica .

Cálculo [ editar ]

Para integrales y derivadas de funciones trigonométricas, consulte las secciones relevantes de Diferenciación de funciones trigonométricas , Listas de integrales y Lista de integrales de funciones trigonométricas . A continuación se muestra la lista de los derivados e integrales de las seis funciones trigonométricas básicas. El número  C es una constante de integración .

{\ displaystyle {\ begin {array} {| r | rr |} f (x) & f '(x) & \ int f (x) \, dx \\\ hline \ sin x & \ cos x & - \ cos x + C \\ cos x & - \ sin x & \ sin x + C \\\ tan x & \ sec ^ {2} x = 1 + \ tan ^ {2} x & - \ ln \ left | \ cos x \ right | + C \\\ cot x & - \ csc ^ {2} x = - (1+ \ cot ^ {2} x) & \ ln \ left | \ sin x \ right | + C \\\ sec x & \ sec x \ tan x & \ ln \ left | \ sec x + \ tan x \ right | + C \\\ csc x & - \ csc x \ cot x & - \ ln \ left | \ csc x + \ cot x \ right | + C \ end { formación}}}

Definiciones usando ecuaciones funcionales [ editar ]

En el análisis matemático , uno puede definir las funciones trigonométricas usando ecuaciones funcionalesbasadas en propiedades como la fórmula de diferencia. Teniendo en cuenta estas fórmulas, se puede probar que solo dos funciones continuas satisfacen esas condiciones. Formalmente, existe exactamente un par de funciones continuas, sin y cos, de modo que para todos los números reales x e y , la siguiente ecuación es válida: ^[17]

$${\ displaystyle \ cos (xy) = \ cos x \ cos y + \ sin x \ sin y \,}

con la condición añadida de que

{\ displaystyle 0

Esto también se puede usar para extender el seno y el coseno a los números complejos. También son posibles otras ecuaciones funcionales para definir funciones trigonométricas.

Computacion [ editar ]

El cálculo de las funciones trigonométricas es un tema complicado, que la mayoría de las personas puede evitar debido a la amplia disponibilidad de computadoras y calculadoras científicas que proporcionan funciones trigonométricas integradas para cualquier ángulo. Esta sección, sin embargo, describe los detalles de su cálculo en tres contextos importantes: el uso histórico de las tablas trigonométricas, las técnicas modernas utilizadas por las computadoras y algunos ángulos "importantes" donde se encuentran fácilmente los valores exactos simples.

El primer paso para calcular cualquier función trigonométrica es la reducción del rango, reduciendo el ángulo dado a un "ángulo reducido" dentro de un rango pequeño de ángulos, por ejemplo 0 a π/2 , utilizando la periodicidad y las simetrías de las funciones trigonométricas.

Artículo principal: Generación de tablas trigonométricas.

Antes de las computadoras, las personas normalmente evaluaban las funciones trigonométricas mediante la interpolación de una tabla detallada de sus valores, calculada a muchas cifras significativas . Dichas tablas han estado disponibles durante el tiempo en que se han descrito las funciones trigonométricas (ver Historial acontinuación), y se generaron típicamente mediante la aplicación repetida de las identidades de media ángulo y adición de ángulo a partir de un valor conocido (como sin ( π/2 ) = 1).

Las computadoras modernas utilizan una variedad de técnicas. ^[18] Un método común, especialmente en procesadores de gama alta con unidades de punto flotante , es combinar una aproximación polinomial o racional(como la aproximación de Chebyshev , la mejor aproximación uniforme y la aproximación de Padé , y generalmente para precisiones más altas o variables, Taylor y Serie Laurent ) con reducción de rango y búsqueda de tabla: primero buscan el ángulo más cercano en una tabla pequeña y luego usan el polinomio para calcular la corrección. ^[19] Dispositivos que carecen de multiplicadores de hardware.a menudo usa un algoritmo llamado CORDIC (así como técnicas relacionadas), que usa solo la suma, la resta, el desplazamiento de bits y la búsqueda de tablas . Estos métodos se implementan comúnmente en unidades de punto flotante de hardwarepor razones de rendimiento.

Para cálculos de precisión muy alta, cuando la convergencia de expansión en serie se vuelve demasiado lenta, las funciones trigonométricas pueden aproximarse mediante la media aritmético-geométrica , que a su vez se aproxima a la función trigonométrica mediante la integral elíptica ( compleja ) . ^[20]

Artículo principal: Constantes trigonométricas exactas

Finalmente, para algunos ángulos simples, los valores se pueden calcular fácilmente a mano usando el teorema de Pitágoras , como en los siguientes ejemplos. Por ejemplo, el seno, coseno y tangente de cualquier múltiplo entero de π/60 radianes (3 °) se pueden encontrar exactamente a mano .

Considere un triángulo rectángulo donde los otros dos ángulos son iguales, y por lo tanto son ambos π/4 radianes (45 °). Entonces la longitud del lado b y la longitud del lado a son iguales; Podemos elegir a = b = 1 . Los valores de seno, coseno y tangente de un ángulo de π/4 radianes (45 °) se pueden encontrar usando el teorema de Pitágoras:

$${\ displaystyle c = {\ sqrt {a ^ {2} + b ^ {2}}} = {\ sqrt {2}} \ ,.}

Por lo tanto:

$${\ displaystyle \ sin {\ frac {\ pi} {4}} = \ sin 45 ^ {\ circ} = \ cos {\ frac {\ pi} {4}} = \ cos 45 ^ {\ circ} = { 1 \ sobre {\ sqrt {2}}} = {{\ sqrt {2}} \ sobre 2}, \,}

$${\ displaystyle \ tan {\ frac {\ pi} {4}} = \ tan 45 ^ {\ circ} = {{\ sin {\ frac {\ pi} {4}}} \ sobre {\ cos {\ frac {\ pi} {4}}}} = {1 \ sobre {\ sqrt {2}}} \ cdot {{\ sqrt {2}} \ sobre 1} = {{\ sqrt {2}} \ sobre {\ sqrt {2}}} = 1. \,}

Cálculo de funciones trigonométricas a partir de un triángulo equilátero.

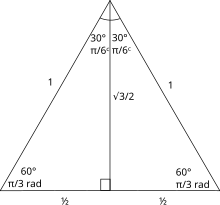
Para determinar las funciones trigonométricas para ángulos de π/3radianes (60 °) y π/6 radianes (30 °), comenzamos con un triángulo equilátero de longitud lateral 1. Todos sus ángulos son π/3 radianes (60 °). Al dividirlo en dos, obtenemos un triángulo rectángulo con π/6 radianes (30 °) y π/3 radians (60 °) ángulos. Para este triángulo, el lado más corto es de 1/2 , el siguiente lado mayor es √ 3/2 y la hipotenusa es 1. Este rendimientos:

$${\ displaystyle \ sin {\ frac {\ pi} {6}} = \ sin 30 ^ {\ circ} = \ cos {\ frac {\ pi} {3}} = \ cos 60 ^ {\ circ} = { 1 \ sobre 2} \ ,,}

$${\ displaystyle \ cos {\ frac {\ pi} {6}} = \ cos 30 ^ {\ circ} = \ sin {\ frac {\ pi} {3}} = \ sin 60 ^ {\ circ} = { {\ sqrt {3}} \ over 2} \ ,,}

$${\ displaystyle \ tan {\ frac {\ pi} {6}} = \ tan 30 ^ {\ circ} = \ cot {\ frac {\ pi} {3}} = \ cot 60 ^ {\ circ} = { 1 \ sobre {\ sqrt {3}}} = {{\ sqrt {3}} \ sobre 3} \ ,.

Valores especiales en funciones trigonométricas [ editar ]

Hay algunos valores especiales de uso común en las funciones trigonométricas, como se muestra en la siguiente tabla.

${\displaystyle {\begin{array}{|c|cccccccc|}{\begin{matrix}{\text{Radian}}\\{\text{Degree}}\end{matrix}}&{\begin{matrix}0\\0^{\circ }\end{matrix}}&{\begin{matrix}{\frac {\pi }{12}}\\15^{\circ }\end{matrix}}&{\begin{matrix}{\frac {\pi }{8}}\\22.5^{\circ }\end{matrix}}&{\begin{matrix}{\frac {\pi }{6}}\\30^{\circ }\end{matrix}}&{\begin{matrix}{\frac {\pi }{4}}\\45^{\circ }\end{matrix}}&{\begin{matrix}{\frac {\pi }{3}}\\60^{\circ }\end{matrix}}&{\begin{matrix}{\frac {5\pi }{12}}\\75^{\circ }\end{matrix}}&{\begin{matrix}{\frac {\pi }{2}}\\90^{\circ }\end{matrix}}\\\hline \sin &0&{\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}&{\frac {\sqrt {2-{\sqrt {2}}}}{2}}&{\frac {1}{2}}&{\frac {\sqrt {2}}{2}}&{\frac {\sqrt {3}}{2}}&{\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}&1\\\cos &1&{\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}&{\frac {\sqrt {2+{\sqrt {2}}}}{2}}&{\frac {\sqrt {3}}{2}}&{\frac {\sqrt {2}}{2}}&{\frac {1}{2}}&{\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}&0\\\tan &0&2-{\sqrt {3}}&{\sqrt {2}}-1&{\frac {\sqrt {3}}{3}}&1&{\sqrt {3}}&2+{\sqrt {3}}&\infty \\\cot &\infty &2+{\sqrt {3}}&{\sqrt {2}}+1&{\sqrt {3}}&1&{\frac {\sqrt {3}}{3}}&2-{\sqrt {3}}&0\\\sec &1&{\sqrt {6}}-{\sqrt {2}}&{\sqrt {2}}{\sqrt {2-{\sqrt {2}}}}&{\frac {2{\sqrt {3}}}{3}}&{\sqrt {2}}&2&{\sqrt {6}}+{\sqrt {2}}&\infty \\\csc &\infty &{\sqrt {6}}+{\sqrt {2}}&{\sqrt {2}}{\sqrt {2+{\sqrt {2}}}}&2&{\sqrt {2}}&{\frac {2{\sqrt {3}}}{3}}&{\sqrt {6}}-{\sqrt {2}}&1\\\end{array}}}$^[21]

El símbolo ∞ aquí representa el punto en el infinito en la línea real proyectivamente extendida , el límite en la línea real extendida es + ∞ en un lado y -∞ en el otro.

Funciones inversas [ editar ]

Artículo principal: Funciones trigonométricas inversas.

Las funciones trigonométricas son periódicas y, por lo tanto, no inyectivas , por lo que estrictamente no tienen una función inversa . Por lo tanto, para definir una función inversa debemos restringir sus dominios para que la función trigonométrica sea biyectiva . A continuación, las funciones de la izquierda están definidas por la ecuación de la derecha; Estas no son identidades probadas. Los principales inversos suelen definirse como:

${\displaystyle {\begin{array}{rrc}{\text{Function}}&{\text{Definition}}&{\text{Value Field}}\\\hline \arcsin x=y&\sin y=x&-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}\\\arccos x=y&\cos y=x&0\leq y\leq \pi \\\arctan x=y&\tan y=x&-{\frac {\pi }{2}}$

Las notaciones sin ⁻¹ y cos ⁻¹ se usan a menudo para las arcosinas y arccos, etc. Cuando se usa esta notación, las funciones inversas podrían confundirse con los inversos multiplicativos de las funciones. La notación que usa el prefijo "arc-" evita tal confusión, aunque "arcsec" para arcsecant puede confundirse con " arcsecond ".

Al igual que el seno y el coseno, las funciones trigonométricas inversas también pueden definirse en términos de series infinitas. Por ejemplo,

$${\ displaystyle \ arcsin z = z + \ left ({\ frac {1} {2}} \ right) {\ frac {z ^ {3}} {3}} + \ left ({\ frac {1 \ cdot 3 } {2 \ cdot 4}} \ right) {\ frac {z ^ {5}} {5}} + \ left ({\ frac {1 \ cdot 3 \ cdot 5} {2 \ cdot 4 \ cdot 6} } \ derecha) {\ frac {z ^ {7}} {7}} + \ cdots \ ,.}

Estas funciones también pueden definirse demostrando que son antiderivadas de otras funciones. El arcsine, por ejemplo, puede escribirse como la siguiente integral:

{\ displaystyle \ arcsin z = \ int _ {0} ^ {z} {\ frac {1} {\ sqrt {1-x ^ {2}}}} \, dx, \ quad | z | <1 .="" font="">

Fórmulas análogas para las otras funciones se pueden encontrar en las funciones trigonométricas inversas . Usando el logaritmo complejo , se pueden generalizar todas estas funciones a argumentos complejos:

{\ displaystyle {\ begin {alineado} \ arcsin z & = - i \ log \ left (iz + {\ sqrt {1-z ^ {2}}} \ right), \, \\\ arccos z & = - i \ log \ left (z + {\ sqrt {z ^ {2} -1}} \ right), \, \\\ arctan z & = {\ frac {1} {2}} i \ log \ left ({\ frac {1 -iz} {1 + iz}} \ right). \ end {alineado}}}

Conexión al producto interno [ editar ]

En un espacio de producto interno , el ángulo entre dos vectores distintos de cero se define como

$${\ displaystyle \ operatorname {angle} (x, y) = \ arccos {\ frac {\ langle x, y \ rangle} {\ | x \ | \ cdot \ | y \ |}}.}

Propiedades y aplicaciones [ editar ]

Artículo principal: Usos de la trigonometría.

Las funciones trigonométricas, como su nombre indica, son de importancia crucial en la trigonometría , principalmente debido a los siguientes dos resultados.

Ley de los senos [ editar ]

La ley de los senos establece que para un triángulo arbitrario con lados a , b y c, y ángulos opuestos a esos lados A , B y C :

$${\ displaystyle {\ frac {\ sin A} {a}} = {\ frac {\ sin B} {b}} = {\ frac {\ sin C} {c}} = {\ frac {2 \ Delta} {a B C}},}

donde Δ es el área del triángulo, o, de manera equivalente,

$${\ displaystyle {\ frac {a} {\ sin A}} = {\ frac {b} {\ sin B}} = {\ frac {c} {\ sin C}} = 2R,}

donde R es el circunferencia del triángulo .

Una curva de Lissajous , una figura formada con una función basada en trigonometría.

Puede probarse dividiendo el triángulo en dos rectos y utilizando la definición anterior de seno. La ley de los senos es útil para calcular las longitudes de los lados desconocidos en un triángulo si se conocen dos ángulos y un lado. Esta es una situación común que ocurre en la triangulación , una técnica para determinar distancias desconocidas mediante la medición de dos ángulos y una distancia encerrada accesible.

Ley de los cosenos [ editar ]

La ley de los cosenos (también conocida como fórmula de coseno o regla de coseno) es una extensión del teorema de Pitágoras :

$${\ displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2ab \ cos C, \,}

o equivalente,

$${\ displaystyle \ cos C = {\ frac {a ^ {2} + b ^ {2} -c ^ {2}} {2ab}}.}

En esta fórmula, el ángulo en C es opuesto al lado  c . Este teorema puede probarse dividiendo el triángulo en dos rectos y utilizando el teorema de Pitágoras .

La ley de los cosenos se puede usar para determinar un lado de un triángulo si se conocen dos lados y el ángulo entre ellos. También se puede utilizar para encontrar los cosenos de un ángulo (y, en consecuencia, los ángulos mismos) si se conocen las longitudes de todos los lados.

Ley de tangentes [ editar ]

Artículo principal: Ley de tangentes.

Lo siguiente todo forma la ley de tangentes ^[22]

$${\ displaystyle {\ frac {\ tan {\ dfrac {AB} {2}}} {\ tan {\ dfrac {A + B} {2}}}} = {\ frac {ab} {a + b}} \,; \ qquad {\ frac {\ tan {\ dfrac {AC} {2}}} {\ tan {\ dfrac {A + C} {2}}}} = {\ frac {ac} {a + c }} \,; \ qquad {\ frac {\ tan {\ dfrac {BC} {2}}} {\ tan {\ dfrac {B + C} {2}}}} = {\ frac {bc} {b + c}}}

La explicación de las fórmulas en palabras sería engorrosa, pero los patrones de sumas y diferencias, para las longitudes y los ángulos opuestos correspondientes, son evidentes en el teorema.

Ley de cotangentes [ editar ]

Artículo principal: Ley de cotangentes

Si

$${\ displaystyle \ zeta = {\ sqrt {{\ frac {1} {s}} (sa) (sb) (sc)}} \} (el radio del círculo inscrito para el triángulo)

y

$${\ displaystyle s = {\ frac {a + b + c} {2}} \} (el semi-perímetro para el triángulo),

entonces todo lo siguiente forma la ley de los cotangentes ^[22]

$${\ displaystyle \ cot {\ frac {A} {2}} = {\ frac {sa} {\ zeta}} \,; \ qquad \ cot {\ frac {B} {2}} = {\ frac {sb } {\ zeta}} \,; \ qquad \ cot {\ frac {C} {2}} = {\ frac {sc} {\ zeta}}}

Resulta que

$${\ displaystyle {\ frac {\ cot {\ dfrac {A} {2}}} {sa}} = {\ frac {\ cot {\ dfrac {B} {2}}} {sb}} = {\ frac {\ cot {\ dfrac {C} {2}}} {sc}}.}

En palabras, el teorema es: la cotangente de un semiángulo es igual a la relación del semiperímetro menos el lado opuesto a dicho ángulo, en el radio del triángulo.

Funciones periódicas [ editar ]

Una animación de la síntesis aditiva de una onda cuadrada con un número creciente de armónicos.

Las funciones de base sinusoidal (parte inferior) pueden formar una onda de diente de sierra (parte superior) cuando se agregan. Todas las funciones básicas tienen nodos en los nodos del diente de sierra, y todas menos la fundamental ( k = 1 ) tienen nodos adicionales. La oscilación vista sobre el diente de sierra cuando k es grande se llama fenómeno de Gibbs

Las funciones trigonométricas también son importantes en la física. Las funciones seno y coseno, por ejemplo, se utilizan para describir el movimiento armónico simple , que modela muchos fenómenos naturales, como el movimiento de una masa unida a un resorte y, para pequeños ángulos, el movimiento pendular de una masa que cuelga de un cuerda. Las funciones seno y coseno son proyecciones unidimensionales de movimiento circular uniforme .

Las funciones trigonométricas también resultan útiles en el estudio de las funciones periódicas generales . Los patrones de onda característicos de las funciones periódicas son útiles para modelar fenómenos recurrentes, como el sonido o las ondas de luz . ^[23]

En condiciones bastante generales, una función periódica f ( x ) se puede expresar como una suma de ondas sinusoidales u ondas de coseno en una serie de Fourier . ^[24]Denotando las funciones de base de seno o coseno por φ _k , la expansión de la función periódica f ( t ) toma la forma:

$${\ displaystyle f (t) = \ sum _ {k = 1} ^ {\ infty} c_ {k} \ varphi _ {k} (t).}

Por ejemplo, la onda cuadrada se puede escribir como la serie de Fourier.

$${\ displaystyle f _ {\ text {square}} (t) = {\ frac {4} {\ pi}} \ sum _ {k = 1} ^ {\ infty} {\ sin {\ big (} (2k- 1) t {\ big)} \ sobre 2k-1}.}

En la animación de una onda cuadrada en la parte superior derecha se puede ver que unos pocos términos ya producen una aproximación bastante buena. La superposición de varios términos en la expansión de una onda de diente de sierra se muestra debajo.

Historia [ editar ]

Artículo principal: Historia de las funciones trigonométricas.

Si bien el estudio inicial de la trigonometría se remonta a la antigüedad, las funciones trigonométricas que se utilizan hoy en día se desarrollaron en el período medieval. La función de acorde fue descubierta por Hiparco de Nicea (180-125 aC) y Ptolomeo del Egipto romano (90-165 CE).

Las funciones seno y coseno se pueden rastrear a las funciones jyā y koti-jyā utilizadas en la astronomía india del período Gupta ( Aryabhatiya , Surya Siddhanta ), a través de la traducción del sánscrito al árabe y luego del árabe al latín. ^[25]

Las seis funciones trigonométricas en uso actual se conocían en las matemáticas islámicas en el siglo noveno, al igual que la ley de los senos, utilizada para resolver triángulos . ^[26] Al-Khwārizmī produjo tablas de senos, cosenos y tangentes. Fueron estudiados por autores como Omar Khayyám , Bhāskara II , Nasir al-Din al-Tusi , Jamshīd al-Kāshī (siglo XIV), Ulugh Beg (siglo XIV), Regiomontanus (1464), Rheticus y el alumno de Rheticus Valentinus Otho .

Madhava de Sangamagrama (c. 1400) logró avances tempranos en el análisis de las funciones trigonométricas en términos de series infinitas . ^[27]

Los términos tangente y secante fueron introducidos por primera vez por el matemático danés Thomas Fincke en su libro Geometria rotundi (1583). ^[28]

El primer uso publicado de las abreviaturas sin , cos y tan es probablemente por el matemático francés del siglo XVI Albert Girard . ^{[ cita requerida ]}

En un artículo publicado en 1682, Leibniz demostró que el pecado x no es una función algebraica de x . ^[29]

La introducción de Leonhard Euler en analysin infinitorum (1748) fue principalmente responsable de establecer el tratamiento analítico de las funciones trigonométricas en Europa, definiéndolas también como series infinitas y presentando la " fórmula de Euler ", así como las abreviaturas casi modernas ( sin. , Cos . , tang. , cuna. , seg. , y cosec. ). ^[25]

Algunas funciones eran comunes históricamente, pero ahora rara vez se usan, como el acorde ( crd ( θ ) = 2 sin ( θ/2 ) ), la versine ( versin ( θ ) = 1 - cos ( θ ) = 2 sin ² ( θ/2 ) ) (que apareció en las tablas más antiguas ^[25] ), la coversina ( coversin ( θ ) = 1 - sin ( θ ) = versin ( π/2 - θ ) ), haversine ( haversin (θ ) = 1/2 versin ( θ ) = sen ² ( θ/2 ) ), ^[30] el exsecante ( exsec ( θ ) = s ( θ ) - 1 ), y la excosecant (excsc ( θ ) = exsec ( π/2 - θ ) = csc ( θ ) - 1 ). Consulte la Lista de identidades trigonométricas para obtener más relaciones entre estas funciones.

Etimología [ editar ]

La palabra sine deriva ^[31] del seno latino , que significa "doblar; bahía", y más específicamente "el pliegue colgante de la parte superior de una toga ", "el pecho de una prenda", que se eligió como la traducción de lo que fue interpretada como la palabra árabe jaib , que significa "bolsillo" o "pliegue" en las traducciones de obras de Al-Battani y al-Khwārizmī del siglo XII al latín medieval . ^[32] La elección se basó en una mala lectura de la forma escrita en árabe jyb ( جيب ),jīvā , que junto con su sinónimo jyā (el término sánscrito estándar para el seno) se traduce como "cuerda de arco", que a su vez se adopta del griego antiguo stringορδή "cadena". ^[33]

La palabra tangente viene del latín tangens que significa "tocar", ya que la línea toca el círculo del radio unitario, mientras que la secante proviene del latín secans - "cortar", desde que la línea corta el círculo. ^[34]

El prefijo " co " (en "coseno", "cotangente", "cosecant") se encuentra en Edmund Gunter 's Canon triangulorum(1620), que define el coseno como una abreviatura para el complementi seno (seno del ángulo complementario ) y procede a definir los cotangens de manera similar.