El exsecante ( exsec , exs ) y excosecant ( excosec , excsc , exc ) son funciones trigonométricas definidos en términos de los secantes y cosecant funciones. Que solían ser importantes en campos como la topografía , la ingeniería ferroviaria , la ingeniería civil , la astronomía , y la trigonometría esférica y podría ayudar a mejorar la precisión, pero rara vez se utilizan hoy en día, excepto para simplificar algunos cálculos.
Exsecante [ editar ]
El exsecante , [2] [3] [4] [5] [6] [7] [8] [9] (Latín: secans exterior [10] [11] [12] [13] ) también conocido como exterior , externo , [1] [14] [15] [16] [17] hacia el exterior o secante exterior y abreviado como exsec [14] [2] [5] [18] [7] [8] [9] [15] [ 16] [19] [20] [21] o exs , [22]es una función trigonométrica definida en términos de la función secante sec ( θ ): [7] [21] [23]
El nombre exsecant se puede entender a partir de una construcción gráfica de las diversas funciones trigonométricas de un círculo unitario , como se usó históricamente. sec ( θ ) es la línea de separación OE , y el exsecante es la parte DE de esta secante que se encuentra en el exterior del círculo (por ejemplo, el latín es el de afuera ).
Excosecante [ editar ]
Una función relacionada es la excosecant [5] [24] o coexsecant , [25] [18] [26]también conocido como exterior , externo , [17] hacia el exterior o cosecant exterior y abreviado como excosec , coexsec , [14] [18 ] [26] excsc [5] [24] o exc , [22] la exsecante del ángulo complementario:
Uso [ editar ]
Importante en campos como topografía , [8] ingeniería ferroviaria [5] (por ejemplo, para trazar curvas de ferrocarril y peralte ), ingeniería civil , astronomía y trigonometría esférica hasta la década de 1980, la función exsecante ahora es poco utilizada. [8] [23] Principalmente, esto se debe a que la amplia disponibilidad de calculadoras y computadoras ha eliminado la necesidad de tablas trigonométricas de funciones especializadas como esta. [8]
La razón para definir una función especial para el exsecante es similar a la razón de ser de la versión : para ángulos pequeños θ , la función seg ( θ ) se aproxima a una , por lo que usar la fórmula anterior para el exsecante implicará la resta de dos casi iguales cantidades, resultando en la cancelación catastrófica . Por lo tanto, una tabla de la función secante necesitaría una precisión muy alta para ser utilizada por el exsecant, haciendo que una tabla especializada exsecant sea útil. Incluso con una computadora, los errores de punto flotante pueden ser problemáticos para exsecantes de ángulos pequeños, si se usa la definición basada en coseno. Una fórmula más precisa en este límite sería usar la identidad:
o
Antes de la disponibilidad de computadoras, esto requeriría multiplicaciones que consumieran mucho tiempo.
La función exsecante fue utilizada por Galileo Galilei en 1632, aunque todavía la llamaba segante (que significa secante ). [27] [28] [29] [30] El término latino secans exterior se usó desde al menos alrededor de 1745. [10] [11] [12] [13] El uso del término inglés secant externo y la abreviatura ej. segundo. Se puede remontar a 1855 cuando Charles Haslett publicó la primera tabla de exsecantes conocida . [1] [31] Variaciones como ex secante y exsecestaban en uso en 1880, [14] y exsecant se utilizó desde 1894 como mínimo. [2]
Los términos coexsecante [25] y coexsec [2] también se pueden usar desde 1880 [2] [25] seguido de excosecantedesde 1909. [5] Albert Einstein también utilizó la función para describir la energía cinética de fermiones . [29] [30]
Identidades matemáticas [ editar ]
Derivados [ editar ]
Integrales [ editar ]
Funciones inversas [ editar ]
Las funciones inversas arcexsecant [26] ( arcexsec , [5] [26] aexsec , [32] [33] aexs , exsec- 1 ) y arcexcosecant ( arcexcosec , arcexcec , [5] aexcsc , aexc , arccoexsecant , arccoexs , cccxexccccc ) 1 ) existe también:
Otras propiedades [ editar ]
Derivado del círculo unitario:
- [5]
- [5]
- La versine o versed sine es una función trigonométrica que ya aparece en algunas de las tablas trigonométricas más antiguas . La versina de un ángulo es igual a 1 menos su coseno .
Descripción general [ editar ]
La versine [2] [3] [4] [5] [6] o sine versed [7] [1] [8] [9] [10] [4] [11] es una función trigonométrica que ya aparece en algunos de Las primeras tablas trigonométricas. Está escrito como versin ( θ ) , [4] [8] [9] sinver ( θ ) , [12] [13]vers ( θ ) , [2] [7] [3] [4] [10] [ 5] [6] ver ( θ )[14] o siv ( θ ) . [15] [16] En latín , se conoce como sinus versus [15] [16] (seno invertido), versinus , versus o sagitta(flecha). [17]Expresado en términos de las funciones senos "verticales" ( sinus rectus ) y cosenos ( cosinus rectus ) que se usan más comúnmente , la versina es igual a 1 - cos ( θ ) , o 2 sen 2 ( θ2 ) .Hay varias funciones relacionadas correspondientes a la versine:- El coseno versado , [18] [nb 1] o vercosine , [18] [nb 1] escrito vercosin ( θ ), vercos ( θ ) [18] o vcs ( θ ) [14]
- El sine coversed , [nb 1] [7] coversine , [3] [5] [6] [8] [9] [19] cosinus frente a [15] [16] [nb 1] o coversinus , escrito carenados ( θ ) , [20] cubre ( θ ) , [7] [3] [5] [6] [10] [13] [19] [21] [22] [23] cosiv ( θ ) [15] [16] [nb 1] o cvs ( θ ) [9][13] [14] [24]
- El coseno cubierto [25] o covercosina , [25] escrito covercosina ( θ ) o covercos ( θ ) [25] o cvc ( θ ) [14]
En analogía con las cuatro funciones mencionadas anteriormente, también existe otro conjunto de cuatro funciones de "medio valor":- El sinusoidales haversed , [26] Haversine [2] [3] [5] [6] [10] [8] [26] o semiversus , [27] [28] escrito Haversin ( θ ) , semiversin ( θ ) , semiversinus ( θ ) , havers ( θ ) , [2] hav ( θ ) , [2] [3] [5] [6] [10] [13] [14] [26] [29] [30] hvs ( θ) , [nb 2] sem ( θ ) [28] o hv ( θ ) , [31] el más famoso de la fórmula de haversine utilizada históricamente en la navegación
- El coseno haversed [32] o havercosine , [32] escrito havercosin ( θ ) , havercos ( θ ) , [32] HAC ( θ ) o HVC ( θ ) [14]
- El seno sin llama , [20] también llamado hacoversina [20] o cohaversina [20] y escrito hacoversin ( θ ) , [20]semicoversin ( θ ) , hacovers ( θ ) , hacov ( θ ) [33] o hcv ( θ ) [14]
- El coseno destruido , [34] también llamado hacovercosina [34] o cohavercosina [34] y escrito como hacovercosina ( θ ) , hacovercos ( θ ) [34] o hcc ( θ ) [14]
Historia y aplicaciones [ editar ]
Versine y coversine [ editar ]
La función sinusoidal ordinaria ( ver nota sobre etimología ) a veces se llama históricamente sinus rectus ("seno vertical"), para contrastarla con el seno versado ( sinus versus ). [36] El significado de estos términos es aparente si uno mira las funciones en el contexto original para su definición, un círculo unitario :Para una cuerda vertical AB del círculo unitario, el seno del ángulo θ (que representa la mitad del ángulo subtendido Δ ) es la distancia AC (mitad de la cuerda). Por otro lado, el seno versado de θ es la distancia CDdesde el centro de la cuerda hasta el centro del arco. Por lo tanto, la suma de cos ( θ ) (igual a la longitud de la línea OC ) y versin ( θ ) (igual a la longitud de la línea CD ) es el radio OD (con longitud 1). Ilustrado de esta manera, el seno es vertical ( recto , literalmente "recto"), mientras que la versina es horizontal (versus , literalmente "vuelto en contra, fuera de lugar"); Ambas son distancias desde C hasta el círculo.Esta figura también ilustra la razón por la cual a la versina a veces se la llamaba sagitta , latín para flecha , [17] [35], del uso árabe sahem [37] del mismo significado. Esto en sí proviene de la palabra india 'sara' (flecha) que se usaba comúnmente para referirse a " utkrama-jya ". Si el arco ADB del ángulo doble Δ = 2 θ se ve como un " arco " y el acorde ABcomo su "cuerda", entonces el CD de versine es claramente el "eje de flecha".Siguiendo con la interpretación del seno como "vertical" y el verso como "horizontal", sagitta es también un sinónimo obsoleto de la abscisa (el eje horizontal de una gráfica). [35]En 1821, Cauchy usó los términos sinus versus versus ( siv ) para la versina y cosinus versus ( cosiv ) para la coversina. [15] [16] [nb 1]Históricamente, el seno versado se consideraba una de las funciones trigonométricas más importantes. [11] [36] [37]Cuando θ va a cero, versin ( θ ) es la diferencia entre dos cantidades casi iguales, por lo que un usuario de una tabla trigonométrica para el coseno solo necesitaría una precisión muy alta para obtener la versine para evitar la cancelación catastrófica , haciendo tablas separadas para el último conveniente. [11] Incluso con una calculadora o computadora, los errores de redondeohacen que sea recomendable utilizar la fórmula sin 2para θ pequeño .Otra ventaja histórica de la versión es que siempre es no negativa, por lo que su logaritmo se define en todas partes excepto en el ángulo único ( θ = 0, 2 π , ...) donde es cero; por lo tanto, uno podría usar tablas logarítmicas Para multiplicaciones en fórmulas que involucran versines.De hecho, la primera tabla de valores de seno (mitad acorde ) de supervivencia (a diferencia de los acordes tabulados por Ptolomeo y otros autores griegos), calculada a partir de la Surya Siddhantha de la India que data del siglo III aC, fue una tabla de valores para el seno y el seno versado (en incrementos de 3.75 ° de 0 a 90 °). [36]El versine aparece como un paso intermedio en la aplicación de la fórmula media de ángulo pecado 2 ( θ2 ) = 12versin ( θ ), derivado por Ptolomeo , que se utilizó para construir dichas tablas.Haversine [ editar ]
El trazo, en particular, fue importante en la navegación porque aparece en la fórmula del trazo , que se usa para calcular con precisión las distancias dentro de la razón en un esferoide astronómico (vea los problemas con el radio de la tierra en comparación con la esfera ) dadas las posiciones angulares (por ejemplo, longitud y latitud ). También se puede usar el pecado 2 ( θ2 ) directamente, pero tener una tabla de la haversina eliminó la necesidad de calcular cuadrados y raíces cuadradas. [11]Una utilización temprana de José de Mendoza y Ríos de lo que más tarde se llamaría haversines se documenta en 1801. [13] [38]El primer equivalente en inglés conocido a una tabla de haversines fue publicado por James Andrew en 1805. [39] [40] [17]En 1835, el término haversine (anotado naturalmente como hav. O base-10 logarítmicamente como log. Haversine o log. Havers. ) Fue acuñado [41] por James Inman [13] [42] [43] en la tercera edición de su Trabajo de navegación y astronomía náutica: para el uso de marineros británicos para simplificar el cálculo de distancias entre dos puntos en la superficie de la tierra utilizando trigonometría esférica para aplicaciones en la navegación. [2] [41] Inman también usó los términos nat. versine y nat. vers. para versines.[2]Otras tablas de alto prestigio de haversines fueron las de Richard Farley en 1856 [39] [44] y John Caulfield Hannyngton en 1876. [39] [45]El haversine se sigue utilizando en la navegación e incluso ha encontrado nuevas aplicaciones en las últimas décadas, como en el método de Bruce D. Stark para despejar distancias lunares utilizando logaritmos gaussianosdesde 1995 [46] [47] o en un método más compacto para la reducción de la vista desde 2014. [31]Usos modernos [ editar ]
Si bien el uso de la versine, coversine y haversine, así como sus funciones inversas se remontan a siglos atrás, los nombres de las otras cinco funciones parecen ser de origen mucho más joven.Un período (0 < θ < π2 ) de una versina o, más comúnmente, una forma de onda haversina (o havercosina) también se usa comúnmente en el procesamiento de señales y la teoría de control como la forma de un pulso o una función de ventana (incluido Hann , Ventanas de Hann – Poisson y Tukey ), porque se suaviza ( continua en valor y pendiente ) "se enciende" de cero a uno (para haversine) y de nuevo a cero. [nb 2] En estas aplicaciones, se denomina función de Hann ofiltro de coseno elevado . Del mismo modo, la havercosina se utiliza en distribuciones de coseno elevado en teoría de probabilidad y estadística .En la forma del pecado 2 ( θ ), la curva del doble ángulo Δ describe la relación entre la propagación y los ángulos en la trigonometría racional , una propuesta de reformulación de geometrías planas y sólidas métricas por Norman John Wildberger desde 2005. [48]Como sagitta y cosagitta, doble ángulo delta variantes de la haversine y havercosine también han encontrado nuevos usos en la descripción de la correlación y anti-correlación de correlacionados fotones en la mecánica cuántica . [49]Identidades matemáticas [ editar ]
Definiciones [ editar ]
[3] [4] [5] [6] [10] [7] [8] [9] [15] [16] 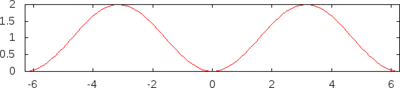
[18] 
[3] [5] [6] [10] [7] [9] [13] [15] [16] [19] [21] [22] [23] [24] 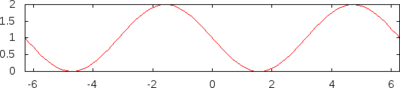
[25] 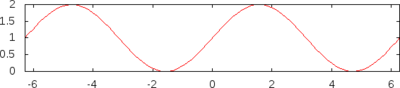
[3] [5] [6] [10] [26] 
[32] 
[20] 
[34] 
Rotaciones circulares [ editar ]
Las funciones son rotaciones circulares entre sí.Derivadas e integrales [ editar ]
[4] [3] [4] [19] [19] [26] [26] Funciones inversas [ editar ]
Funciones inversas como arcversine [33] (arcversin, arcvers, [7] [33] avers, [50] [51] aver), arcvercosine(arcvercosin, arcvercos, avercos, avcs), arccoversine [33] (arccoversin, arccovers, [ 7] [33] recupera, [50] [51] acvs), arccovercosine (arccovercosin, arccovercos, acovercos, acvc), archaversine (archaversin, archav, [33] haversin −1 , [52] invhav, [33] [53 ] [54] [55] ahav, [33][50] [51] Ahvs, ahv, hav −1 [56] [57] ), archavercosina (archavercosin, archavercos, ahvc), archacoversine (archacoversin, ahcv) o archacovercosine (archacovercosin, archacovercosin, ahcc) existen también:Otras propiedades [ editar ]
Aproximaciones [ editar ]
Cuando la versina v es pequeña en comparación con el radio r , se puede aproximar a partir de la longitud de la mitad de la cuerda L (la distancia AC mostrada arriba) por la fórmula- . [58]
Alternativamente, si la versine es pequeña y se conocen la versine, el radio y la longitud de la mitad de la cuerda, se pueden usar para estimar la longitud del arco s ( AD en la figura anterior) mediante la fórmulaEsta fórmula era conocida por el matemático chino Shen Kuo , y dos siglos después, Guo Shoujing desarrolló una fórmula más precisa que también involucraba a la sagitta . [59]Curvas arbitrarias y acordes [ editar ]
El término versine también se usa a veces para describir desviaciones de la rectitud en una curva plana arbitraria, de las cuales el círculo anterior es un caso especial. Dado un acorde entre dos puntos en una curva, la distancia perpendicular v desde el acorde a la curva (generalmente en el punto medio del acorde) se llama medición de versine . Para una línea recta, la versina de cualquier acorde es cero, por lo que esta medida caracteriza la rectitud de la curva. En el límite a medida que la longitud del acorde L va a cero, la relación 8 vL 2 va a la curvatura instantánea . Este uso es especialmente común en el transporte ferroviario., donde describe las medidas de la rectitud de las vías del carril [61] y es la base del método Hallade para el levantamiento de vías .








![\ int \ operatorname {exsec} (\ theta) \, \ mathrm {d} \ theta = \ ln \ left [\ cos \ left ({\ frac {\ theta} {2}} \ right) + \ sin \ left ({\ frac {\ theta} {2}} \ right) \ right] - \ ln \ left [\ cos \ left ({\ frac {\ theta} {2}} \ right) - \ sin \ left ({ \ frac {\ theta} {2}} \ right) \ right] - \ theta + C](https://wikimedia.org/api/rest_v1/media/math/render/svg/4023beda8fb65a34b16efb3b5d4ca17302b8b82e)
![{\ displaystyle \ int \ operatorname {excsc} (\ theta) \, \ mathrm {d} \ theta = \ ln \ left [\ tan \ left ({\ frac {\ theta} {2}} \ right) \ right ] - \ theta + C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38a6dcd03b3efddd2ef0bb822bf70f9505556913)
























































No hay comentarios:
Publicar un comentario