TRIGONOMETRÍA

El error de Abbe , que lleva el nombre de Ernst Abbe , también llamado error de seno , describe el aumento del error angular en la distancia. Por ejemplo, cuando uno mide un punto que está a 1 metro de distancia a 45 grados, un error angular de 1 grado corresponde a un error de posición de más de 1.745 cm, equivalente a un error de medición de distancia de 1.745%. ^[1]

En el diseño de máquinas, algunos componentes son particularmente sensibles a los errores angulares. Por ejemplo, leves desviaciones del paralelismo del eje del husillo de un torno al movimiento de la herramienta a lo largo del lecho de la máquina pueden llevar a un estrechamiento relativamente grande (no deseado) a lo largo de la parte (es decir, una parte no cilíndrica). Los calibradores a vernier no están libres de error de abe, mientras que los calibres de tornillo están libres de error de abbe. El error de Abbe es el producto del desplazamiento de Abbe y el seno del error angular en el sistema.

El error de abate puede ser perjudicial para el cómputo muerto .

Fórmula:

$${\ displaystyle \ epsilon = h \ sin \ theta}

$${\ displaystyle \ epsilon} el error.

$${\ displaystyle h} la distancia.

$${\ displaystyle \ theta} el ángulo.

Este artículo necesita citas adicionales para su verificación . Por favor, ayudar a mejorar este artículo mediante la adición de citas de fuentes confiables . El material sin fuente puede ser desafiado y eliminado.  Encuentre fuentes:  "Condición sine de Abbe"  -  noticias  · periódicos  · libros  · erudito  ·JSTOR ( diciembre de 2009 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla)

Los ángulos de entrada y salida de cada rayo que pasa a través de un sistema de imágenes (recuadro gris) están relacionados. Cuando el sistema de imágenes obedece a la condición sinusoidal de Abbe, la proporción de los senos de estos ángulos es igual a la ampliación (lateral absoluta) del sistema.

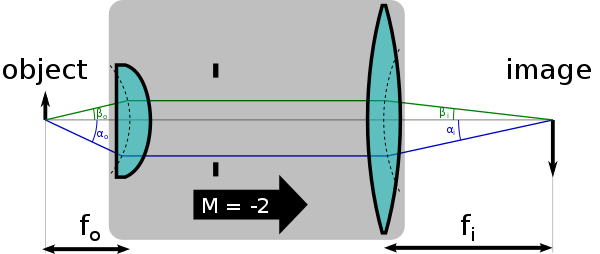
La condición sinusoidal de Abbe es una condición que debe cumplir una lente u otro sistema óptico para que pueda producir imágenes nítidas de objetos fuera del eje y en el eje. Fue formulado por Ernst Abbe en el contexto de los microscopios . ^[1]

La condición sine de Abbe dice que

el seno del ángulo del objeto-espacio$${\ textstyle \ alpha _ {o}} Debe ser proporcional al seno del ángulo del espacio de la imagen. $${\ textstyle \ alpha _ {i}}

Además, la relación es igual a la ampliación del sistema. En términos matemáticos esto es:

$${\ displaystyle {\ frac {\ sin \ alpha _ {o}} {\ sin \ alpha _ {i}}} = {\ frac {\ sin \ beta _ {o}} {\ sin \ beta _ {i} }} = | M |}

donde las variables $${\ textstyle (\ alpha _ {o}, \ beta _ {o})} son los ángulos (en relación con el eje óptico) de cualquiera de los dos rayos cuando salen del objeto, y $${\ textstyle (\ alpha _ {i}, \ beta _ {i})}son los ángulos de los mismos rayos donde alcanzan el plano de la imagen (por ejemplo, el plano de película de una cámara). Por ejemplo, ($${\ textstyle \ alpha _ {o}, \ alpha _ {i})}podría representar un rayo paraxial (es decir, un rayo casi paralelo al eje óptico), y$${\ textstyle (\ beta _ {o}, \ beta _ {i})}podría representar un rayo marginal (es decir, un rayo con el ángulo más grande admitido por la apertura del sistema). Se dice que un sistema de imágenes ópticas para el cual esto es cierto para todos los rayos obedece la condición de seno de Abbe.

La ampliación y la condición sinusoidal de Abbe [ editar ]

Un sistema óptico de imágenes (caja gris) que obedece a la condición sinusoidal tiene una relación fija entre los senos de los ángulos de los rayos en la entrada y salida del sistema. $${\ textstyle {\ frac {\ sin \ alpha _ {o}} {\ sin \ alpha _ {i}}} = M}. Esta relación es igual a la ampliación (M).

Usando el marco de la óptica de Fourier , podemos explicar fácilmente el significado de la condición sinusoidal de Abbe. Decir que un objeto en el plano de objeto de un sistema óptico tiene una función de transmisión de la forma, T ( x _o , y _o ). Podemos expresar esta función de transmisión en términos de su transformada de Fourier como

$${\ displaystyle T (x_ {o}, y_ {o}) = \ iint T (k_ {x}, k_ {y}) ~ e ^ {j (k_ {x} x_ {o} + k_ {y} y_ {o})} ~ dk_ {x} \, dk_ {y}.}

Ahora, supongamos por simplicidad que el sistema no tiene distorsión de la imagen , de modo que las coordenadas del plano de la imagen están relacionadas linealmente con las coordenadas del plano del objeto a través de la relación

$${\ displaystyle x_ {i} = Mx_ {o} \,}

$${\ displaystyle y_ {i} = Mi_ {o} \,}

donde M es la ampliación del sistema . La transmitancia del plano del objeto anterior puede ahora reescribirse en una forma ligeramente modificada:

$${\ displaystyle T (x_ {o}, y_ {o}) = \ iint T (k_ {x}, k_ {y}) ~ e ^ {j ((k_ {x} / M) (Mx_ {o}) + (k_ {y} / M) (My_ {o}))} ~ dk_ {x} \, dk_ {y}}

donde los diversos términos se han multiplicado y dividido simplemente en el exponente por M , la ampliación del sistema. Ahora, las ecuaciones se pueden sustituir por las coordenadas del plano de la imagen en términos de coordenadas del plano del objeto, para obtener,

$${\ displaystyle T (x_ {i}, y_ {i}) = \ iint T (k_ {x}, k_ {y}) ~ e ^ {j ((k_ {x} / M) x_ {i} + ( k_ {y} / M) y_ {i})} ~ dk_ {x} \, dk_ {y}}

En este punto se puede proponer otra transformación de coordenadas ( i . E ., La condición sine Abbe) relativa el plano del objeto número de onda del espectro para el plano de imagen de número de onda del espectro como

$${\ displaystyle k_ {x} ^ {i} = {\ frac {k_ {x}} {M}}}

$${\ displaystyle k_ {y} ^ {i} = {\ frac {k_ {y}} {M}}}

para obtener la ecuación final para el campo del plano de la imagen en términos de coordenadas del plano de la imagen y números de referencia del plano de la imagen como:

$${\ displaystyle T (x_ {i}, y_ {i}) = M ^ {2} \ iint T (Mk_ {x} ^ {i}, Mk_ {y} ^ {i}) ~ e ^ {j (k_ {x} ^ {i} x_ {i} + k_ {y} ^ {i} y_ {i})} dk_ {x} ^ {i} \, dk_ {y} ^ {i}}

A partir de la óptica de Fourier , se sabe que los números de onda se pueden expresar en términos del sistema de coordenadas esféricas como

$${\ displaystyle k_ {x} = k \ sin \ theta \ cos \ varphi \,}

$${\ displaystyle k_ {y} = k \ sin \ theta \ sin \ varphi \,}

Si se considera un componente espectral para el cual $${\ displaystyle \ varphi = 0}, entonces la transformación de coordenadas entre el objeto y el plano de imagen wavenumbers toma la forma

$${\ displaystyle k ^ {i} \ sin \ theta ^ {i} = k {\ frac {\ sin \ theta} {M}}.

Esta es otra forma de escribir la condición sinusoidal de Abbe, que simplemente refleja el principio de incertidumbre clásico para los pares de transformadas de Fourier, a saber, que a medida que se amplía la extensión espacial de cualquier función (por el factor de ampliación, M ), la extensión espectral se contrae de la misma manera. Factor, M , de modo que el producto de ancho de banda espacial permanezca constante.

En trigonometría , es común usar mnemónicos para recordar las identidades trigonométricas y las relaciones entre las diversas funciones trigonométricas .

SOH-CAH-TOA [ editar ]

Las relaciones seno , coseno y tangente en un triángulo rectángulo se pueden recordar representándolas como cadenas de letras, por ejemplo, SOH-CAH-TOA en inglés:

S ine = O pposite ÷ H ypotenuse

C osine = A dcacent ÷ H ypotenuse

T angent = O pposite ÷ A djacent

Una forma de recordar las letras es a tocarlas fonéticamente (es decir / ˌ s oʊ k ə t oʊ . Ə / SOH -kə- TOH -ə ). ^[1]

Otro método es ampliar las letras en una frase, como " S OMe O ld H ags C An't A lways H ide T heredera O ld Age", " S OMe O ld H ippy C algo A tro H ippy T rippin' o n a cid "o frases que puedan ser más apropiado para las personas más jóvenes como" S OMe o ld H orse C AME A'Hopping T hrough O ur A lley "y " S itting O n H ard Concrete A lways H urts T manguera O uter A reas" Otra nemotécnico que se enseña comúnmente en las escuelas irlandés es:." C ome A nd H ave S Ome O rangos H elp T o O vercome A mnesia ". ^[2]

Las comunidades en los círculos chinos pueden elegir recordarlo como TOA-CAH-SOH, que también significa "mujer de pie grande" ( chino : 大腳 嫂 ; Pe̍h-ōe-jī : tōa-kha-só ) en Hokkien .

Una forma alternativa de recordar las cartas para Sin, Cos, y Tan es memorizar las sílabas sin sentido Oh, Ah, Oh-Ah (es decir, / oʊ ə oʊ . Ə / ) para O / H, A / H, O / A . O, para recordar las seis funciones, Sin, Cos, Tan, Cot, Sec y Csc, memorice las sílabas O / H, A / H, Oh / Ah, Ah / Oh, H / A, H / O (es decir, / oʊ ə oʊ . ə ə oʊ h ə h oʊ /).

Todos los estudiantes toman cálculo [ editar ]

Signos de funciones trigonométricas en cada cuadrante.

Todas las S os estudiantes T ake C alculus es un mnemónico para el signo de cada funciones trigonométricas en cada cuadrante del plano. Las letras ASTC indican cuáles de las funciones trigonométricas son positivas, comenzando en el primer cuadrante superior derecho y moviéndose en sentido contrario a las agujas del reloj a través de los cuadrantes 2 a 4.

• Cuadrante I (ángulos de 0 a 90 grados, o 0 a π / 2 radianes): todaslas funciones trigonométricas son positivas en este cuadrante.
• Cuadrante II (ángulos de 90 a 180 grados, o π / 2 a π radianes): las funciones S ine y cosecant son positivas en este cuadrante.
• Cuadrante III (ángulos de 180 a 270 grados, o π a 3π / 2 radianes): las funciones de agente y cotangente son positivas en este cuadrante.
• Cuadrante IV (ángulos de 270 a 360 grados, o 3π / 2 a 2π radianes): C osine y funciones secantes son positivos en este cuadrante.

Otros mnemotécnicos incluyen:

• Todas las S taciones T o C entral ^[3]
• Todas las S illy T om C ATS ^[3]
• A dd S ugar T o C offee ^[3]
• Todos los clientes de S cience T (son) C razy ^[4]

Otros mnemónicos fáciles de recordar son las leyes ACTS y CAST . Estos tienen las desventajas de no ir secuencialmente de los cuadrantes 1 a 4 y no reforzar la convención de numeración de los cuadrantes.

• CAST sigue en el sentido contrario a las agujas del reloj, pero comienza en el cuadrante 4 y atraviesa los cuadrantes 4, 1, 2 y luego 3.
• ACTS aún comienza en el cuadrante 1, pero va en el sentido de las agujas del reloj pasando por los cuadrantes 1, 4, 3 y luego 2.

Cuadro hexagonal [ editar ]

Identidades trigonométricas mnemotécnicas.

Otra mnemotécnica permite que todas las identidades básicas se lean rápidamente. Aunque la parte de la palabra mnemotécnica utilizada para construir el gráfico no se mantiene en inglés ^{[se necesita aclaración ]} , el gráfico en sí es bastante fácil de reconstruir con un poco de reflexión. Las funciones sin "co" aparecen a la izquierda, las co-funciones a la derecha, un 1 va en el centro, los triángulos apuntan hacia abajo y todo el dibujo se ve como un trébol de refugio . ^[5]

Comenzando en cualquier esquina del hexágono:

• La esquina inicial es igual a una sobre la esquina opuesta.
• Al ir en sentido horario o antihorario, la esquina inicial es igual a la esquina siguiente dividida por la esquina después de eso.
• La esquina de inicio es igual al producto de sus dos vecinos más cercanos.
• La suma de los cuadrados de cada elemento en la parte superior de un triángulo es igual al cuadrado del elemento en la parte inferior. Estas son las identidades trigonométricas de Pitágoras :

$${\ displaystyle \ sin ^ {2} A + \ cos ^ {2} A = 1 \}

$${\ displaystyle 1+ \ cot ^ {2} A = \ csc ^ {2} A \}

$${\ displaystyle \ tan ^ {2} A + 1 = \ sec ^ {2} A \}

Aparte de la última viñeta, los valores específicos para cada identidad se resumen en esta tabla:

Función de arranque	... es igual a uno sobre el opuesto	... es igual al primero sobre el segundo, yendo en sentido horario	... es igual al primero sobre el segundo, yendo en sentido contrario a las agujas del reloj	... es igual al producto de dos vecinos más cercanos
$${\ displaystyle \ tan A}	$${\ displaystyle = {1 / \ cot A}}	$${\ displaystyle = {\ sin A / \ cos A}}	$${\ displaystyle = {\ sec A / \ csc A}}	$${\ displaystyle = \ sin A \ cdot \ sec A}
$${\ displaystyle \ sin A}	$${\ displaystyle = {1 / \ csc A}}	$${\ displaystyle = {\ cos A / \ cot A}}	$${\ displaystyle = {\ tan A / \ sec A}}	$${\ displaystyle = \ cos A \ cdot \ tan A}
$${\ displaystyle \ cos A}	$${\ displaystyle = {1 / \ sec A}}	$${\ displaystyle = {\ cot A / \ csc A}}	$${\ displaystyle = {\ sin A / \ tan A}}	$${\ displaystyle = \ sin A \ cdot \ cot A}
$${\ displaystyle \ cot A}	$${\ displaystyle = {1 / \ tan A}}	$${\ displaystyle = {\ csc A / \ sec A}}	$${\ displaystyle = {\ cos A / \ sin A}}	$${\ displaystyle = \ cos A \ cdot \ csc A}
$${\ displaystyle \ csc A}	$${\ displaystyle = {1 / \ sin A}}	$${\ displaystyle = {\ sec A / \ tan A}}	$${\ displaystyle = {\ cot A / \ cos A}}	$${\ displaystyle = \ cot A \ cdot \ sec A}
$${\ displaystyle \ sec A}	$${\ displaystyle = {1 / \ cos A}}	$${\ displaystyle = {\ tan A / \ sin A}}	$${\ displaystyle = {\ csc A / \ cot A}}	$${\ displaystyle = \ csc A \ cdot \ tan A}