TRIGONOMETRÍA

La tabla sinusoidal de Āryabhaṭa es un conjunto de veinticuatro números dados en el tratado astronómico Āryabhaṭīya, compuesto por el matemático y astrónomo indio del siglo quinto ṭryabhaṭa (476–550 CE), para el cálculo de las medias cuerdas de ciertos conjuntos de arcos de un círculo. . No es una tabla en el sentido moderno de una tabla matemática; es decir, no es un conjunto de números organizados en filas y columnas. ^[1] [2]

Arco y acorde de un círculo.

La tabla de Āryabhaṭa tampoco es un conjunto de valores de la función seno trigonométrica en un sentido convencional; es una tabla de las primeras diferencias de los valores de senos trigonométricos expresados ​​en minutos de arco , y debido a esto, la tabla también se conoce como tabla de diferencias sinusoidales de Āryabhaṭa . ^[3] [4]

La mesa de Āryabhaṭa fue la primera mesa sinusoidal jamás construida en la historia de las matemáticas . ^[5] Las tablas ahora perdidas de Hiparco (c.190 aC - c.120 aC) y Menelao (c.70-140 CE) y las de Ptolomeo (c.AD 90 - c.168) eran todas tablas de acordes y No de medias cuerdas. ^[5] La mesa de Āryabhaṭa se mantuvo como la mesa sinusoidal estándar de la antigua India. Hubo intentos continuos para mejorar la precisión de esta tabla. Estos esfuerzos culminaron en el descubrimiento final de las expansiones de la serie de potencias de las funciones seno y coseno por Madhava de Sangamagrama (c.1350 - c.1425), el fundador de laEscuela de astronomía y matemáticas de Kerala , y la tabulación de una tabla sinusoidal de Madhava con valores precisos de siete u ocho lugares decimales.

Algunos historiadores de las matemáticas han argumentado que la tabla sinusoidal dada en inryabhaṭiya era una adaptación de tablas anteriores construidas por matemáticos y astrónomos de la antigua Grecia. ^[6] David Pingree , uno de los principales historiadores de las ciencias exactas de la antigüedad en los Estados Unidos, fue un exponente de tal visión. Suponiendo esta hipótesis, GJ Toomer ^{[7] [8] [9]} escribe: "Casi no existe documentación para la llegada más temprana de los modelos astronómicos griegos a la India, o para el caso cómo se habrían visto esos modelos. Así que es muy difícil para determinar hasta qué punto lo que nos llega representa el conocimiento transmitido, y lo que es original para los científicos indios ... La verdad es probablemente una mezcla enredada de ambos ".

La tabla [ editar ]

La tabla original [ editar ]

Este artículo contiene texto índico. Sin el soporte de reproducciónadecuado , puede ver signos de interrogación o cuadros , vocales fuera de lugar o coyunturas faltantes en lugar de texto Indic.

La estrofa en Āryabhaṭiya que describe la tabla sinusoidal se reproduce a continuación:

     भखि ्हस स्ग किष्झ श्घकि किघ्व | 
     ्लकि किग्र हक्य ्ग झश ङ्व क्ल प्त छ कला-अर्ध-ज्यास् ||

En notaciones modernas [ editar ]

Los valores codificados en el verso sánscrito de Āryabhaṭa se pueden decodificar usando el esquema numéricoexplicado en Āryabhaṭīya , y los números decodificados se enumeran en la tabla a continuación. En la tabla, las medidas de los ángulos relevantes para la tabla sinusoidal de Āryabhaṭa se enumeran en la segunda columna. La tercera columna contiene la lista de los números contenidos en el verso sánscrito que figura anteriormente en la escritura de Devanagari . Para la comodidad de los usuarios que no pueden leer Devanagari, estos números de palabras se reproducen en la cuarta columna de la transliteración ISO 15919 . La siguiente columna contiene estos números en los números hindú-árabes.. Los números de Āryabhaṭa son las primeras diferencias en los valores de los senos. El valor correspondiente de seno (o más precisamente, de jya ) se puede obtener sumando las diferencias hasta esa diferencia. Así, el valor de jya correspondiente a 18 ° 45 ′ es la suma 225 + 224 + 222 + 219 + 215 = 1105. Para evaluar la precisión de los cálculos de Āryabhaṭa, los valores modernos de jya s se dan en la última columna de la tabla.

En la tradición matemática india, el seno (o jya ) de un ángulo no es una proporción de números. Es la longitud de un determinado segmento de línea, un cierto medio acorde. El radio del círculo base es un parámetro básico para la construcción de dichas tablas. Históricamente, varias tablas se han construido utilizando diferentes valores para este parámetro. Āryabhaṭa ha elegido el número 3438 como el valor del radio del círculo base para el cálculo de su tabla sinusoidal. El fundamento de la elección de este parámetro es la idea de medir la circunferencia de un círculo en medidas de ángulos. En los cálculos astronómicos, las distancias se miden en grados , minutos , segundos., etc. En esta medida, la circunferencia de un círculo es 360 ° = (60 × 360) minutos = 21600 minutos. El radio del círculo, la medida de cuya circunferencia es 21600 minutos, es 21600 / 2π minutos. Al calcular esto utilizando el valor π = 3.1416 conocido por Aryabhata, se obtiene el radio del círculo en aproximadamente 3438 minutos. La tabla sinusoidal de Āryabhaṭa se basa en este valor para el radio del círculo base. Todavía no se ha establecido quién es el primero en utilizar este valor para el radio base. Pero Aryabhatiyaes el primer texto sobreviviente que contiene una referencia a esta constante básica. ^[11]

Sl. No	Ángulo (A)  (engrados ,  minutos de arco )	Valor en la  notación numérica de Āryabhaṭa (en Devanagari )	Valor en la  notación numérica de Āryabhaṭa (en transliteraciónISO 15919 )	Valor en  [números hindú-árabes]	El  valor deĀryabhaṭade  jya (A)	Valor moderno  de jya (A) (3438 × sin (A))
1	03 ° 45 ′	मखि	makhi	225	225 ′	224.8560
2	07 ° 30 ′	भखि	bhakhi	224	449 ′	448.7490
3	11 ° 15 ′	फखि	phakhi	222	671 ′	670.7205
4	15 ° 00 ′	धखि	dhakhi	219	890 ′	889.8199
5	18 ° 45 ′	णखि	ṇakhi	215	1105 ′	1105.1089
6	22 ° 30 ′	ञखि	ñakhi	210	1315 ′	1315.6656
7	26 ° 15 ′	ङखि	ṅakhi	205	1520 ′	1520.5885
8	30 ° 00 ′	्झ	hasjha	199	1719 ′	1719.0000
9	33 ° 45 ′	्ककि	Skaki	191	1910 ′	1910.0505
10	37 ° 30 ′	्ग	kiṣga	183	2093 ′	2092.9218
11	41 ° 15 ′	्घकि	śghaki	174	2267 ′	2266.8309
12	45 ° 00 ′	्व	Kighva	164	2431 ′	2431.0331
13	48 ° 45 ′	्लकि	ghlaki	154	2585 ​​′	2584.8253
14	52 ° 30 ′	्र	Kigra	143	2728 ′	2727.5488
15	56 ° 15 ′	्य	hakya	131	2859 ′	2858.5925
dieciséis	60 ° 00 ′	धकि	dhaki	119	2978 ′	2977.3953
17	63 ° 45 ′	किच	kica	106	3084 ′	3083.4485
18	67 ° 30 ′	्ग	sga	93	3177 ′	3176.2978
19	71 ° 15 ′	झश	jhaśa	79	3256 ′	3255.5458
20	75 ° 00 ′	्व	ṅva	sesenta y cinco	3321 ′	3320.8530
21	78 ° 45 ′	्ल	kla	51	3372 ′	3371.9398
22	82 ° 30 ′	्त	pta	37	3409 ′	3408.5874
23	86 ° 15 ′	फ	pha	22	3431 ′	3430.6390
24	90 ° 00 ′	छ	cha	7	3438 ′	3438.0000

Método computacional de Āryabhaṭa [ editar ]

La segunda sección de Āryabhaṭiya titulada Ganitapādd a contiene una estrofa que indica un método para el cálculo de la tabla sinusoidal. Hay varias ambigüedades en la interpretación correcta del significado de este versículo. Por ejemplo, la siguiente es una traducción del verso dado por Katz en el que las palabras entre corchetes son inserciones del traductor y no traducciones de textos en el verso. ^[11]

• "Cuando la segunda mitad del [acorde] dividido es menor que la primera mitad del acorde, que es [aproximadamente igual a] el arco [correspondiente], en una cierta cantidad, las [diferencias seno] restantes son menos [que la anterior] unos cada uno por esa cantidad de eso dividido por el primer medio acorde ".

Esto puede estar refiriéndose al hecho de que la segunda derivada de la función seno es igual al negativo de la función seno.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

El problema del cinturón

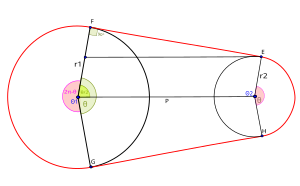
El problema de la correaes una matemáticasproblema que requiere encontrar la longitud de un cruzado de la correa que conecta dos circulares poleas con radio r ₁ y r ₂cuyos centros están separados por una distancia P . La solución del problema de la banda requiere trigonometría y los conceptos de la línea bitangente , el ángulo vertical y los ángulos congruentes .

Solución [ editar ]

Claramente, los triángulos ACO y ADO son triángulos congruentes en ángulo recto , al igual que los triángulosBEO y BFO. Además, los triángulos ACO y BEO son similares . Por lo tanto, los ángulos CAO, DAO, EBO y FBO son todos iguales. Denotando este ángulo por$${\ displaystyle \ varphi}(denominado en radianes ), la longitud del cinturón es

$${\ displaystyle CO + DO + EO + FO + {\ text {arc}} CD + {\ text {arc}} EF \, \!}

$${\ displaystyle = 2r_ {1} \ tan (\ varphi) + 2r_ {2} \ tan (\ varphi) + (2 \ pi -2 \ varphi) r_ {1} + (2 \ pi -2 \ varphi) r_ {2} \, \!}

$${\ displaystyle = 2 (r_ {1} + r_ {2}) (\ tan (\ varphi) + \ pi - \ varphi) \, \!}

Esto explota la conveniencia de denominar ángulos en radianes que la longitud de un arco = el radio × la medida del ángulo hacia el arco .

Encontrar $${\ displaystyle \ varphi}Vemos en la similitud de los triángulos ACO y BEO que

$${\ displaystyle {\ frac {AO} {BO}} = {\ frac {AC} {BE}} \, \!}

$${\ displaystyle \ Rightarrow {\ frac {Px} {x}} = {\ frac {r_ {1}} {r_ {2}}} \, \!}

$${\ displaystyle \ Rightarrow {\ frac {P} {x}} = {\ frac {r_ {1} + r_ {2}} {r_ {2}}} \, \!}

$${\ displaystyle \ Rightarrow {x} = {\ frac {Pr_ {2}} {r_ {1} + r_ {2}}} \, \!}

$${\ displaystyle \ cos (\ varphi) = {\ frac {r_ {2}} {x}} = {\ frac {r_ {2}} {\ left ({\ dfrac {Pr_ {2}} {r_ {1 } + r_ {2}}} \ right)}} = {\ frac {r_ {1} + r_ {2}} {P}} \, \!}

$${\ displaystyle \ Rightarrow \ varphi = \ cos ^ {- 1} \ left ({\ frac {r_ {1} + r_ {2}} {P}} \ right) \, \!}

Para P fijo, la longitud de la correa depende solo de la suma de los valores de radio r ₁  +  r ₂ , y no de sus valores individuales.

Problema de la polea [ editar ]

El problema de la polea.

Hay otros tipos de problemas similares al problema de la correa. El problema de la polea , como se muestra, es similar al problema de la correa; Sin embargo, el cinturón no se cruza. En el problema de la polea la longitud de la correa es

$${\ displaystyle 2P \ sin \ left ({\ frac {\ theta} {2}} \ right) + r_ {1} (2 \ pi - \ theta) + r_ {2} {\ theta} \ ,,}

donde r ₁ representa el radio de la polea más grande, r ₂representa el radio de la más pequeña, y:

$${\ displaystyle \ theta = 2 \ cos ^ {- 1} \ left ({\ frac {r_ {1} -r_ {2}} {P}} \ right) \ ,.}

Aplicaciones [ editar ]

El problema de las correas se usa ^[1] en el diseño de aviones , engranajes de bicicletas , automóviles y otros artículos con poleas o correas que se cruzan entre sí. El problema de la polea también se usa en el diseño de cintas transportadoras que se encuentran en las bandas de equipaje de los aeropuertos y en las líneas de fábrica automatizadas .

la fórmula de aproximación sinusoidal de Bhaskara I es una expresión racional en una variable para el cálculo de los valores aproximados de los senos trigonométricos descubiertos por Bhaskara I (c. 600 - c. 680), un matemático indio del siglo VII . ^[1] Esta fórmula se da en su tratado titulado Mahabhaskariya . No se sabe cómo Bhaskara llegué a su fórmula de aproximación. Sin embargo, varios historiadores de las matemáticas.han presentado diferentes hipótesis sobre el método que Bhaskara podría haber usado para llegar a su fórmula. La fórmula es elegante, simple y le permite a uno calcular valores razonablemente precisos de senos trigonométricos sin usar geometría alguna.

La fórmula de aproximación [ editar ]

La fórmula se da en los versículos 17 a 19, Capítulo VII, Mahabhaskariya de Bhaskara I. A continuación se ofrece una traducción de los versos: ^[3]

• (Ahora) Enuncio brevemente la regla (para encontrar el bhujaphala y el kotiphala , etc.) sin hacer uso de las diferencias de Rsine 225, etc. Resta los grados de un bhuja (o koti ) de los grados de un semicírculo ( es decir, 180 grados). Luego multiplica el resto por los grados de bhuja o koti y anota el resultado en dos lugares. En un lugar, reste el resultado de 40500. Por una cuarta parte del resto (así obtenido), divida el resultado en el otro lugar multiplicado por el ' anthyaphala (es decir, el radio epicíclico). De este modo se obtiene toda la bahuphala (o, kotiphala) para el sol, la luna o los planetas estelares. Así también se obtienen las Rsines directas e inversas.

(La referencia "Rsine-diferencias 225" es una alusión a la tabla sinusoidal de Aryabhata ).

En las notaciones matemáticas modernas, para un ángulo x en grados, esta fórmula da ^[3]

$${\ displaystyle \ sin x ^ {\ circ} \ approx {\ frac {4x (180-x)} {40500-x (180-x)}}}

Formas equivalentes de la fórmula [ editar ]

La fórmula de aproximación sinusoidal de Bhaskara I se puede expresar utilizando la medida en radianes de los ángulos de la siguiente manera. ^[1]

$${\ displaystyle \ sin x \ approx {\ frac {16x (\ pi -x)} {5 \ pi ^ {2} -4x (\ pi -x)}}.}

Para un entero positivo n toma la siguiente forma: ^[4]

$${\ displaystyle \ sin {\ frac {\ pi} {n}} \ approx {\ frac {16 (n-1)} {5n ^ {2} -4n + 4}}.

La fórmula adquiere una forma aún más simple cuando se expresa en términos del coseno en lugar del seno. Usando la medida de radianes para el ángulo, y poniendo$${\ displaystyle x = {\ tfrac {1} {2}} \ pi + y}, uno obtiene

$${\ displaystyle \ cos y \ approx {\ frac {\ pi ^ {2} -4y ^ {2}} {\ pi ^ {2} + y ^ {2}}}.}

La asonancia de "$${\ displaystyle \ pi}"y"$${\ displaystyle y}"hace esta expresión especialmente agradable como mnemotécnica.

Formas equivalentes de la fórmula de Bhaskara I fueron dadas por casi todos los astrónomos y matemáticos subsiguientes de la India. Por ejemplo, Brhma-Sphuta-Siddhanta de Brahmagupta (598 - 668 CE ) (versículos 23 - 24, Capítulo XIV) ^[3] da la fórmula de la siguiente forma:

$${\ displaystyle R \ sin x ^ {\ circ} \ approx {\ frac {Rx (180-x)} {10125 - {\ frac {1} {4}} x (180-x)}}}

Además, Bhaskara II (1114 - 1185 CE ) ha dado esta fórmula en su Lilavati (Kshetra-vyavahara, Soka No.48) en la siguiente forma:

$${\ displaystyle 2R \ sin x ^ {\ circ} \ approx {\ frac {4 \ times 2R \ times 2Rx \ times (360R-2Rx)} {{\ frac {1} {4}} \ times 5 \ times ( 360R) ^ {2} -2Rx \ times (360R-2Rx)}}}

Precisión de la fórmula [ editar ]

La figura ilustra el nivel de precisión de la fórmula de aproximación sinusoidal de Bhaskara I. Las curvas desplazadas 4 x (180 - x ) / (40500 - x (180 - x )) - 0.2 y sin ( x) + 0.2 parecen copias exactas de la curva sin ( x ).

La fórmula es aplicable para valores de x ° en el rango de 0 a 180. La fórmula es muy precisa en este rango. Las gráficas de sin ( x ) y la fórmula de aproximación son indistinguibles y son casi idénticas. Una de las figuras adjuntas proporciona la gráfica de la función de error, a saber, la función,

$${\ displaystyle \ sin x ^ {\ circ} - {\ frac {4x (180-x)} {40500-x (180-x)}}}

en el uso de la fórmula. Muestra que el error absoluto máximo en el uso de la fórmula es de alrededor de 0.0016. A partir de una gráfica del valor porcentual del error absoluto, queda claro que el error porcentual máximo es menor que 1.8. La fórmula de aproximación proporciona valores de senos suficientemente precisos para todos los propósitos prácticos. Sin embargo, no fue suficiente para los requisitos computacionales más precisos de la astronomía. La búsqueda de fórmulas más precisas por parte de los astrónomos indios finalmente llevó al descubrimiento de las expansiones de las series de poder de sin x y cos x por Madhava de Sangamagrama (c. 1350 - c. 1425), el fundador de la escuela de astronomía y matemáticas de Kerala .

Gráfica del error en la fórmula de aproximación sinusoidal de Bhaskara I

Gráfica del porcentaje de error en la fórmula de aproximación sinusoidal de Bhaskara I

Derivación de la fórmula [ editar ]

Bhaskara no había indicado ningún método por el cual llegó a su fórmula. Los historiadores han especulado sobre diversas posibilidades. Aún no se han obtenido respuestas definitivas. Más allá de su importancia histórica de ser un excelente ejemplo de los logros matemáticos de los antiguos astrónomos indios, la fórmula también es importante desde una perspectiva moderna. Los matemáticos han intentado derivar la regla utilizando conceptos y herramientas modernos. Se han sugerido alrededor de media docena de métodos, cada uno basado en un conjunto separado de premisas. ^[2] [3] La mayoría de estas derivaciones usan solo conceptos elementales.

Derivación basada en geometría elemental ^[2] [3] [ editar ]

Deje que la circunferencia de un círculo se mida en grados y que el radio R del círculo también se mida en grados . Seleccionando un diámetro fijo AB y un punto arbitrario P en el círculo y dejando caer la PMperpendicular a AB , podemos calcular el área del triángulo APB de dos maneras. Igualando las dos expresiones para el área que se obtiene (1/2) AB × PM = (1/2) AP × BP . Esto da

$${\ displaystyle {\ frac {1} {PM}} = {\ frac {AB} {AP \ times BP}}}.

Si x es la longitud del arco AP , la longitud del arco BP es 180 - x . Estos arcos son mucho más grandes que los acordes respectivos. Por lo tanto uno obtiene

{\ displaystyle {\ frac {1} {PM}}> {\ frac {2R} {x (180-x)}}}.

Uno busca ahora dos constantes α y β tales que

$${\ displaystyle {\ frac {1} {PM}} = \ alpha {\ frac {2R} {x (180-x)}} + \ beta}

De hecho, no es posible obtener tales constantes. Sin embargo, uno puede elegir valores para α y β, de modo que la expresión anterior sea válida para dos valores elegidos de la longitud de arco x . Eligiendo 30 ° y 90 ° como estos valores y resolviendo las ecuaciones resultantes, uno obtiene inmediatamente la fórmula de aproximación sinusoidal de Bhaskara I.

Derivación comenzando con una expresión racional general [ editar ]

Suponiendo que x está en radianes, uno puede buscar una aproximación al pecado ( x ) en la siguiente forma:

$${\ displaystyle \ sin x \ approx {\ frac {a + bx + cx ^ {2}} {p + qx + rx ^ {2}}}}

Las constantes de un , b , c , p , q y r (sólo cinco de ellos son independientes) pueden determinarse suponiendo que la fórmula debe ser exactamente válida cuando x = 0, π / 6, π / 2, π, y además asumiendo que tiene que satisfacer la propiedad de que sin ( x ) = sin (π - x ). ^[2] [3] Este procedimiento produce la fórmula expresada usando la medida en radianes de los ángulos.

Un argumento elemental ^[4] [ editar ]

Comparación de las gráficas de las parábolas 
x (180 - x ) / 8100 y x (180 - x ) / 9000 
con la gráfica de sin ( x ) ( x en grados).

La parte del gráfico de sin ( x ) en el rango de 0 ° a 180 ° "parece" parte de una parábola a través de los puntos (0, 0) y (180, 0). La general tal parábola es

$${\ displaystyle kx (180-x).}

La parábola que también pasa por (90, 1) (que es el punto correspondiente al valor sin (90 °) = 1) es

$${\ displaystyle {\ frac {x (180-x)} {90 \ times 90}} = {\ frac {x (180-x)} {8100}}.}

La parábola que también pasa a través de (30, 1/2) (que es el punto correspondiente al valor sin (30 °) = 1/2) es

$${\ displaystyle {\ frac {x (180-x)} {2 \ times 30 \ times 150}} = {\ frac {x (180-x)} {9000}}.}

Estas expresiones sugieren un denominador variable que toma el valor 90 × 90 cuando x  = 90 y el valor 2 × 30 × 150 cuando x  = 30. Que esta expresión también debe ser simétrica con respecto a la línea ' x  = 90' elimina la posibilidad de Escogiendo una expresión lineal en  x . Los cálculos que involucran x (180 -  x ) podrían sugerir inmediatamente que la expresión podría ser de la forma

$${\ displaystyle 8100a + bx (180-x).}

Un poco de experimentación (o configurando y resolviendo dos ecuaciones lineales en a y b ) arrojará los valores a  = 5/4, b  = −1/4. Estos dan la fórmula de aproximación sinusoidal de Bhaskara I.