Polígonos

 eneagrama (del griego εννεα, ennea, «nueve», y γράμμα, gramma, «trazo») es una estrella de nueve puntas. Es llamado en ocasiones nonagrama.

Eneagrama regular[editar]

Un eneagrama regular (un polígono estrellado de nueve lados) es construido utilizando los mismos puntos que un eneágono regular pero conectado en pasos fijos. Tiene dos formas, representadas por un símbolo de Schläfli como {9/2} y {9/4}, conectando cada segundo y cuarto puntos respectivamente.

Existe también una figura estrellada, {9/3} o 3{3}, hecha a partir de los puntos de un eneágono regular pero conectados como un compuesto de tres triángulos equiláteros.¹​²​ (Si los triángulos están entrelazados de manera alternada, resulta en un enlace Brunniano.) Esta figura estrellada es conocida en ocasiones como la estrella de Goliat, siendo {6/2} o 2{3} la estrella de David.³​

Grafo completo K9

Eneágono {9/1}

Polígono estrellado {9/2}

Figura estrellada 3{3}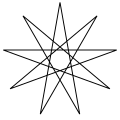

Polígono estrellado {9/4}

Otras figuras de eneagramas[editar]

La estelación final del icosaedrotiene caras de eneagrama 2-isogonales. Es un poliedro estrellado 9/4, pero los vértices no están igualmente espaciados.

El Eneagrama de la personalidad y el eneagrama del Cuarto Camino utilizan un eneagrama irregular que consiste en un triángulo y un hexagrama irregular.

La estrella de nueve puntas bahá'í.

Uso en la cultura popular[editar]

• Slipknot, una banda de heavy metal, utiliza el eneagrama de la figura estrellada |9/3| como su símbolo. [1]
• La estrella de nueve puntas puede simbolizar los nueve regalos o frutos del espíritu santo.

eneágono o nonágono, de "9" lados es un polígonode nueve lados y nueve vértices. El nombre proviene del griegoenneagonon, (εννεα, nueve + γωνον, esquina), mientras que nonágonoproviene del latín (nonus, nueve + gonon).

Construcción[editar]

No es posible construir un eneágono regular con regla y compás, pero existe una forma aproximada:

Propiedades[editar]

Un eneágono tiene 27 diagonales, resultado que se puede obtener aplicando la ecuación general para determinar el número de diagonales de un polígono, ${\displaystyle D=n(n-3)/2}$; siendo el número de lados ${\displaystyle n=9}$, tenemos:

${\displaystyle D={\frac {9(9-3)}{2}}=27}$

La suma de todos los ángulos internos de cualquier eneágono es 1260 grados ó ${\displaystyle 7\pi }$ radianes.

Eneágono regular[editar]

Un eneágono regular es el que tiene todos sus lados de la misma longitud y todos sus ángulos internos iguales. Cada ángulo interno del eneágono regular mide 140º ó ${\displaystyle 7\pi /9}$ rad. Cada ángulo externo del eneágono regular mide 40º ó ${\displaystyle 2\pi /9}$ rad.

Al multiplicar la longitud t de un lado de un eneágono regular por nueve (el número de lados n del polígono) obtendremos la longitud de su perímetro P.

${\displaystyle P=n\cdot t=9\ t}$

El área de un eneágono regular de lado t puede calcularse de la siguiente forma:

${\displaystyle A={\frac {9(t^{2})}{4\tan({\frac {\pi }{9}})}}\simeq 6,1818\ t^{2}}$

donde ${\displaystyle \pi }$ es la constante pi y ${\displaystyle \tan }$ es la función tangente calculada en radianes.

Si se conoce la longitud del apotema a del polígono, otra alternativa para calcular el área es:

${\displaystyle A={\frac {P\cdot a}{2}}={\frac {9(t)\ a}{2}}}$

eneágono es un polígono de nueve lados y nueve vértices.

Eneágono regular

Un eneágono regular es un polígono de nueve lados y nueve ángulos iguales.

Ángulos del eneágono

Suma de ángulos interiores de un eneágono = (9 − 2) · 180° = 1260°

El valor de un ángulo interior del eneágono regular es 1260º : 9 = 140º

El ángulo central del eneágono regular mide: 360º : 9 = 40º

Diagonales del eneágono

Número de diagonales = 9 · (9 − 3) : 2 = 27

Perímetro del eneágono regular

Perímetro = 9 · l

Área del eneágono regular

https://www.ditutor.com

La estelación, es un proceso para construir nuevos polígonos (en dos dimensiones), poliedros (en tres dimensiones), o en general politopos de ndimensiones. El proceso consiste en extender elementos, tales como bordes o planos, por lo general de forma simétrica, hasta que vuelvan a encontrarse. La nueva figura es una estelación de la anterior.

Polígonos estelados[editar]

La estelación de un polígono regular, da como resultado un polígono estrellado regular. Un polígono regular estrellado es representado por su símbolo de Schläfli {n/m}, donde n es el número de vértices, m es el pasousado en la secuenciación de las aristas de su alrededor, siendo m y n son coprimos (no tienen divisores comunes).

Haciendo m = 1 se convierte en el polígono convexo usual {n}.