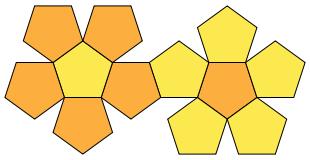
desarrollo de un poliedro es la sucesión ordenada en un plano de polígonos unidos por sus lados, de forma que se puedan doblar (por los bordes) para formar las caras del poliedro. Los desarrollos de poliedros son útiles a la hora de estudiar los cuerpos geométricos, ya que gracias a ellos se pueden construir las figuras geométricas utilizando diferentes materiales como por ejemplo papel o cartón.
Es una cuestión abierta desde hace mucho tiempo si todos los poliedros convexos P (aquellos poliedros cuyos ángulos diedros entre bordes valen 180 grados) tienen desarrollo: si la superficie de P puede ser cortada a lo largo de los bordes y ser desarrollada como un polígono plano (sin solapamiento). (Este contorno a veces se denota como el despliegue del poliedro) Este problema explícito se planteó en un artículo de Shephard. La historia y los progresos sobre esta cuestión se discutieron en la Parte III de los Algoritmos de la Geometría Plegable. Si la restricción de que los cortes sean sobre los bordes del poliedro permite los cortes a través del interior de las caras, entonces existen varios métodos para cortar y desplegar un poliedro convexo sobre un polígono plano. Por ejemplo, cortar a lo largo del lugar geométrico de un punto de corte sería suficiente.
Además, en un desarrollo bien hecho, la ruta más corta (sobre la superficie) entre dos puntos de la superficie de un poliedro se corresponde con una línea recta. Dicha línea debe estar completamente dentro del desarrollo, aunque se pueden considerar diferentes desarrollos para ver cual de ellos ofrece da el camino más corto. Por ejemplo, en el caso de un cubo, si los puntos están en caras adyacentes el camino más corto puede ser aquel que cruza el vértice común; en estos casos el camino más corto se obtiene con un desarrollo en el que las dos caras también sean adyacentes. Otros posibles candidatos a ser el camino más corto son aquellos que pasan a través de la superficie de una tercera cara adyacente a ambos, y los desarrollos correspondientes se pueden utilizar para encontrar el camino más corto en cada caso.


diagonal es todo segmento que une dos vértices no consecutivos de un polígono o de un poliedro. En sentido coloquial, una diagonal es una recta o segmento con cierta inclinación o un conjunto de elementos alineados de esta manera.

Etimología[editar]
La palabra diagonal proviene del griego diagonios (saco), utilizada tanto por Estrabón1 como por Euclides2 para referirse al segmento que conecta dos vértices de un rombo o cuboide,3 y formada por dia- ("a través") y gonia ("ángulo", relacionada a gony, "rodilla"), luego adoptada en latín como diagonus .
Número de diagonales de un polígono[editar]
En un polígono de n lados, el número de diagonales viene dado por la ecuación:
| Este resultado se obtiene razonando de la siguiente manera: a partir de cada uno de los n vértices pueden trazarse n - 3 diagonales, pues no hay diagonales hacia sí mismo ni hacia los 2 vértices adyacentes. Dado que la diagonal que va de un vértice A a otro B y la que viene de ese vértice B de regreso al vértice A son la misma diagonal, se divide por dos para evitar contar esta diagonal dos veces. |
Matriz matemática[editar]
Con el mismo criterio, se habla de diagonal secundaria superior o inferior para referirse a los elementos inmediatamente por encima o por debajo, respectivamente, de la diagonal principal. Con la misma definición de Aque se dio antes, los elementos conforman la diagonal secundaria superior, mientras que los elementos conforman la diagonal secundaria inferior.con el mismo criterio, se habla de un diagonal.
Otros usos del término[editar]
Se denomina calle diagonal (o simplemente diagonal) a toda calle que, en un trazado de calles paralelas, una intersecciones rompiendo este esquema. Por extensión una diagonal sirve para referirse a los elementos inmediatamente por encima o por debajo de la diagonal principal.

coordenadas cartesianas se han representado las curvas de algunas raíces, así como de sus potencias, en el intervalo [0,1]. La diagonal, de ecuación y = x, es eje de simetría entre cada curva y la curva de su inversa
Un dodecágono, en la geometría plana , es un polígono de 12 lados y 12 vértices a la vez.
Si al prolongar un lado, toda la figura queda exactamente en uno de los semiplanos determinados por el lado y sus prolongaciones, el polígono es convexo.
En el caso de que exista un lado con sus prolongaciones y determina que la figura quede en los dos semiplanos definidos por tal lado y sus prolongaciones, el polígono es cóncavo.
Si al prolongar un lado, toda la figura queda exactamente en uno de los semiplanos determinados por el lado y sus prolongaciones, el polígono es convexo.
En el caso de que exista un lado con sus prolongaciones y determina que la figura quede en los dos semiplanos definidos por tal lado y sus prolongaciones, el polígono es cóncavo.
La suma de sus ángulos interiores es 1800°.
Propiedades[editar]
Un dodecágono tiene 54 diagonales, resultado que se puede obtener aplicando la ecuación general para deteminar el número de diagonales de un polígono, ; siendo el número de lados , tenemos:
La suma de todos los ángulos internos de cualquier dodecágono es 1800 grados ó radianes.
El ángulo central de un dodecágono regular es de 30º.
El ángulo central de un dodecágono regular es de 30º.
El número de puntos en que se intersecan las diagonales de un dodecágono regular es 495.
Dodecágono regular[editar]
Un dodecágono regular es un dodecágono con igual longitud en todos sus lados y cuyos ángulos internostienen todos la misma medida: 150º ó rad. Cada ángulo externo del dodecágono regular mide 30º ó rad.
Al multiplicar la longitud t de un lado de un dodecágono regular por doce (el número de lados n del polígono) obtendremos la longitud de su perímetro P.
El área A de un dodecágono regular se puede calcular a partir de la longitud t de uno de sus lados de la siguiente forma:
Si se conoce la longitud de la apotema a del polígono, otra alternativa para esto es:
También se puede saber el área a través de la fórmula:
donde r es el radio del círculo circunscrito al dodecágono.
Su área representa los del área del hexágono regular inscrito en la misma circunferencia.
Construcción de un dodecágono regular[editar]
Este polígono regular se puede construir con un compás y con una regla. La siguiente animación son los 23 pasos a realizar, a tener en cuenta que desde el paso 8 al 11, no se modifica el radio del compás.
















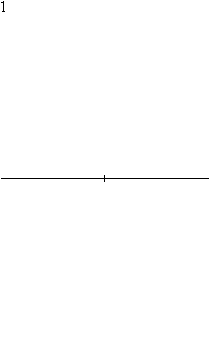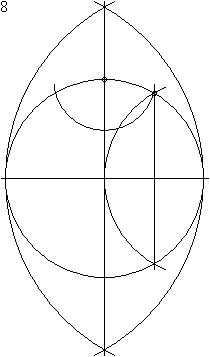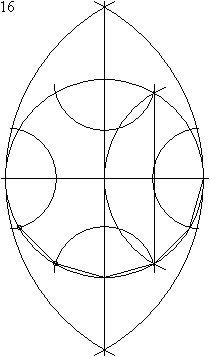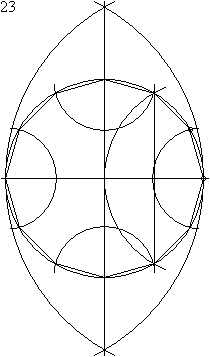
No hay comentarios:
Publicar un comentario