IMÁGENES MÉDICAS - ELECTROFISIOLOGÍA

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Figura. 1: Vista simplificada de una fibra neuronal de la teoría del cable.

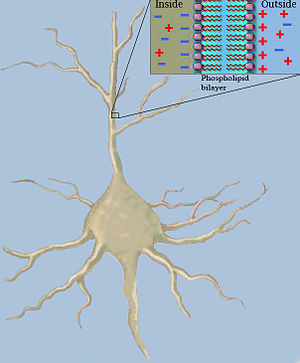
La teoría clásica del cable utiliza modelos matemáticospara calcular la corriente eléctrica (y el voltaje que loacompaña ) a lo largo de neuritas ^[a] pasivas , particularmente las dendritas que reciben entradas sinápticas en diferentes sitios y tiempos. Las estimaciones se realizan modelando dendritas y axones como cilindros compuestos de segmentos con capacidades $${\ displaystyle c_ {m}}y resistencias $${\ displaystyle r_ {m}}combinados en paralelo (ver fig. 1). La capacitancia de una fibra neuronal se produce porque lasfuerzas electrostáticas actúan a través de la bicapa lipídica muy delgada (ver Figura 2). La resistencia en serie a lo largo de la fibra.$${\ displaystyle r_ {l}}Se debe a la significativa resistencia del axoplasma al movimiento de carga eléctrica .

Historia [ editar ]

La teoría del cable en la neurociencia computacional tiene sus raíces en la década de 1850, cuando el profesor William Thomson (más tarde conocido como Lord Kelvin) comenzó a desarrollar modelos matemáticos de decaimiento de la señal en cables telegráficos submarinos (submarinos). Los modelos se parecían a las ecuaciones diferenciales parciales utilizadas por Fourier para describir la conducción de calor en un cable.

La década de 1870 vio los primeros intentos de Hermann para modelar los potenciales electrotónicos neuronalestambién al centrarse en las analogías con la conducción de calor. Sin embargo, fue Hoorweg quien descubrió por primera vez las analogías con los cables submarinos de Kelvin en 1898 y luego Hermann y Cremer desarrollaron de forma independiente la teoría de los cables para las fibras neuronales a principios del siglo XX. Cole y Hodgkin (1920s-1930s) desarrollaron teorías matemáticas adicionales sobre la conducción de fibras nerviosas basadas en la teoría del cable , Offner et al. (1940), y Rushton (1951).

La evidencia experimental de la importancia de la teoría del cable para modelar el comportamiento de los axonescomenzó a surgir en la década de 1930 a partir del trabajo realizado por Cole, Curtis, Hodgkin, Sir Bernard Katz , Rushton, Tasaki y otros. Dos documentos clave de esta época son los de Davis y Lorente de Nó (1947) y Hodgkin y Rushton (1946).

La década de 1950 vio mejoras en las técnicas para medir la actividad eléctrica de neuronas individuales . Por lo tanto, la teoría del cable se volvió importante para analizar los datos recopilados a partir de grabaciones de microelectrodos intracelulares y para analizar las propiedades eléctricas de las dendritas neuronales . Los científicos como Coombs, Eccles , Fatt, Frank, Fuortes y otros ahora confiaban en gran medida en la teoría del cable para obtener información funcional de las neuronas y para guiarlos en el diseño de nuevos experimentos.

Más tarde, la teoría del cable con sus derivados matemáticos permitió que los trabajadores como Jack, Rall , Redman, Rinzel, Idan Segev, Tuckwell, Bell e Iannella exploraran modelos de neuronas cada vez más sofisticados .

Derivando la ecuación del cable [ editar ]

Tenga en cuenta, existen varias convenciones de r _m . Aquí, r _m y c _m , como se introdujo anteriormente, se miden por unidad de longitud de membrana (por metro (m)). Por lo tanto, r _m se mide en ohm · metros (Ω · m) y c _m en faradios por metro (F / m). Esto contrasta con R _m (en Ω · m²) y C _m (en F / m²), que representan la resistencia específica y la capacitancia, respectivamente, de una unidad de área de membrana (en m ² ). Por lo tanto, si se conoce el radio, a , del axón, ^[b] entonces su circunferencia es 2πa , y su r _m , y sus valores de c _m se pueden calcular como:

$${\ displaystyle r_ {m} = {\ frac {R_ {m}} {2 \ pi a \}}}

( 1 )

$${\ displaystyle c_ {m} = C_ {m} 2 \ pi a \}

( 2 )

Estas relaciones tienen sentido de manera intuitiva, ya que cuanto mayor sea la circunferencia del axón, mayor será el área de escape de la carga a través de su membrana y, por lo tanto, menor será la resistencia de la membrana (que divide R _m por 2 πa ); y cuanta más membrana haya disponible para almacenar la carga (multiplicando C _m por 2 πa ). La resistencia eléctrica específica , ρ _l , del axoplasma permite calcular la resistencia intracelular longitudinal por unidad de longitud, r _l , (en Ω · m ⁻¹ ) mediante la ecuación:

$${\ displaystyle r_ {l} = {\ frac {\ rho _ {l}} {\ pi a ^ {2} \}}}

( 3 )

Cuanto mayor sea el área de la sección transversal del axón, πa ², mayor será el número de trayectorias para que la carga fluya a través de su axoplasma, y ​​menor será la resistencia axoplasmática.

Varias vías importantes de extender la teoría clásica del cable han visto recientemente la introducción de estructuras endógenas para analizar los efectos de la polarización de proteínas dentro de las dendritas y diferentes distribuciones de entradas sinápticas sobre la superficie dendrítica de una neurona.

Para comprender mejor cómo se deriva la ecuación del cable, primero simplifique aún más la neurona teórica y pretenda que tiene una membrana perfectamente sellada ( r _m = ∞) sin pérdida de corriente hacia el exterior y sin capacitancia ( c _m  = 0). Una corriente inyectada en la fibra ^[c] en la posición x  = 0 se movería a lo largo del interior de la fibra sin cambios. Alejándonos del punto de inyección y utilizando la ley de Ohm ( V  =  IR ) podemos calcular el cambio de voltaje como:

$${\ displaystyle \ Delta V = -i_ {l} r_ {l} \ Delta x \}

( 4 )

donde lo negativo es porque la corriente fluye hacia abajo del gradiente potencial.

Dejando que Δ x vaya hacia cero y teniendo incrementos infinitamente pequeños de x , se puede escribir ( 4 ) como:

$${\ displaystyle {\ frac {\ parcial V} {\ parcial x}} = - i_ {l} r_ {l} \}

( 5 )

o

$${\ displaystyle {\ frac {1} {r_ {l}}} {\ frac {\ parcial V} {\ parcial x}} = - i_ {l} \}

( 6 )

Llevar r _m nuevamente dentro del cuadro es como hacer agujeros en una manguera de jardín. Cuantos más orificios, más rápido escapará el agua de la manguera, y menos agua viajará desde el comienzo de la manguera hasta el final. De manera similar, en un axón, parte de la corriente que viaja longitudinalmente a través del axoplasma escapará a través de la membrana.

Si i _m es la corriente que se escapa a través de la membrana por unidad de longitud, m, entonces la corriente total que se escapa a lo largo de las unidades y debe ser y · i _m . Por lo tanto, el cambio de corriente en el axoplasma, Δ i _l , a la distancia, Δ x , desde la posición x = 0 se puede escribir como:

$${\ displaystyle \ Delta i_ {l} = - i_ {m} \ Delta x \}

( 7 )

O bien, utilizando incrementos continuos, infinitesimalmente pequeños:

$${\ displaystyle {\ frac {\ partial i_ {l}} {\ partial x}} = - i_ {m} \}

( 8 )

$${\ displaystyle i_ {m}}se puede expresar con otra fórmula, incluyendo la capacitancia. La capacitancia causará un flujo de carga (una corriente) hacia la membrana en el lado del citoplasma. Esta corriente se suele denominar corriente de desplazamiento (aquí se denota$${\ displaystyle i_ {c}}.) El flujo solo tendrá lugar mientras no se haya alcanzado la capacidad de almacenamiento de la membrana. $${\ displaystyle i_ {c}} entonces se puede expresar como:

$${\ displaystyle i_ {c} = c_ {m} {\ frac {\ partial V} {\ partial t}} \}

( 9 )

dónde $${\ displaystyle c_ {m}} es la capacitancia de la membrana y $${\ displaystyle {\ partial V} / {\ partial t}}Es el cambio de voltaje en el tiempo. La corriente que pasa por la membrana ($${\ displaystyle i_ {r}}) se puede expresar como:

$${\ displaystyle i_ {r} = {\ frac {V} {r_ {m}}}}

( 10 )

y porqué $${\ displaystyle i_ {m} = i_ {r} + i_ {c}} la siguiente ecuación para $${\ displaystyle i_ {m}} se puede derivar si no se agrega una corriente adicional desde un electrodo:

$${\ displaystyle {\ frac {\ partial i_ {l}} {\ partial x}} = - i_ {m} = - \ left ({\ frac {V} {r_ {m}}} + c_ {m} { \ frac {\ parcial V} {\ parcial t}} \ derecha)}

( 11 )

dónde $${\ displaystyle {\ partial i_ {l}} / {\ partial x}} Representa el cambio por unidad de longitud de la corriente longitudinal.

La combinación de las ecuaciones ( 6 ) y ( 11 ) da una primera versión de una ecuación de cable:

$${\ displaystyle {\ frac {1} {r_ {l}}} {\ frac {\ parcial ^ {2} V} {\ parcial x ^ {2}}} = c_ {m} {\ frac {\ parcial V } {\ partial t}} + {\ frac {V} {r_ {m}}}}

( 12 )

que es una ecuación diferencial parcial de segundo orden (PDE).

Mediante un simple reordenamiento de la ecuación ( 12 ) (ver más adelante) es posible hacer que aparezcan dos términos importantes, a saber, la constante de longitud (a veces denominada la constante de espacio) denotada$${\ displaystyle \ lambda}y la constante de tiempo denotada $${\ displaystyle \ tau}. Las siguientes secciones se centran en estos términos.

Constante de longitud [ editar ]

Artículo principal: Longitud constante.

La constante de longitud, $${\ displaystyle \ lambda}(lambda), es un parámetro que indica hasta qué punto una corriente estacionaria influirá en el voltaje a lo largo del cable. Cuanto mayor sea el valor de$${\ displaystyle \ lambda}, cuanto más lejos fluirá la carga. La constante de longitud se puede expresar como:

$${\ displaystyle \ lambda = {\ sqrt {\ frac {r_ {m}} {r_ {l}}}}}

( 13 )

Cuanto mayor sea la resistencia de la membrana, r _m , mayor será el valor de$${\ displaystyle \ lambda}y, mientras más corriente permanezca dentro del axoplasma, viajará longitudinalmente a través del axón. Cuanto mayor es la resistencia axoplasmática,$${\ displaystyle r_ {l}}, cuanto menor sea el valor de $${\ displaystyle \ lambda}Cuanto más difícil sea que la corriente viaje a través del axoplasma, y ​​más corta podrá viajar la corriente. Es posible resolver la ecuación ( 12 ) y llegar a la siguiente ecuación (que es válida en condiciones de estado estacionario, es decir, cuando el tiempo se acerca al infinito):

$${\ displaystyle V_ {x} = V_ {0} e ^ {- {\ frac {x} {\ lambda}}}}

( 14 )

Dónde $${\ displaystyle V_ {0}} es la despolarización en $${\ displaystyle x = 0}(punto de inyección de corriente), e es la constante exponencial (valor aproximado 2.71828) y$${\ displaystyle V_ {x}}es el voltaje a una distancia dada x desde x = 0. Cuando$${\ displaystyle x = \ lambda} entonces

$${\ displaystyle {\ frac {x} {\ lambda}} = 1}

( 15 )

y

$${\ displaystyle V_ {x} = V_ {0} e ^ {- 1}}

( 16 )

lo que significa que cuando medimos $${\ displaystyle V} a distancia $${\ displaystyle \ lambda} desde $${\ displaystyle x = 0} obtenemos

$${\ displaystyle V _ {\ lambda} = {\ frac {V_ {0}} {e}} = 0.368V_ {0}}

( 17 )

Así $${\ displaystyle V _ {\ lambda}} Siempre es el 36.8 por ciento de $${\ displaystyle V_ {0}}.

Constante de tiempo [ editar ]

Artículo principal: Constante de tiempo

Los neurocientíficos a menudo están interesados ​​en saber qué tan rápido es el potencial de membrana, $${\ displaystyle V_ {m}}, de un axón cambia en respuesta a cambios en la corriente inyectada en el axoplasma. La constante de tiempo,$${\ displaystyle \ tau}, es un índice que proporciona información sobre ese valor. $${\ displaystyle \ tau} Se puede calcular como:

$${\ displaystyle \ tau = r_ {m} c_ {m}. \}

( 18 )

Cuanto mayor sea la capacitancia de la membrana, $${\ displaystyle c_ {m}}, cuanto más corriente se necesita para cargar y descargar un parche de membrana y más tiempo llevará este proceso. Cuanto mayor sea la resistencia de la membrana$${\ displaystyle r_ {m}}Cuanto más difícil es para una corriente inducir un cambio en el potencial de membrana. Así que cuanto mayor sea la$${\ displaystyle \ tau}cuanto más lento puede viajar el impulso nervioso. Eso significa que el potencial de la membrana (voltaje a través de la membrana) se retrasa más detrás de las inyecciones de corriente. Los tiempos de respuesta varían de 1 a 2 milisegundos en neuronas que procesan información que necesita una alta precisión temporal de 100 milisegundos o más. Un tiempo de respuesta típico es de unos 20 milisegundos.

Forma genérica y estructura matemática [ editar ]

Si uno multiplica la ecuación ( 12 ) por$${\ displaystyle r_ {m}} en ambos lados del signo igual obtenemos:

$${\ displaystyle {\ frac {r_ {m}} {r_ {l}}} {\ frac {\ parcial ^ {2} V} {\ parcial x ^ {2}}} = c_ {m} r_ {m} {\ frac {\ parcial V} {\ parcial t}} + V}

( 19 )

y reconocer $${\ displaystyle \ lambda ^ {2} = {r_ {m}} / {r_ {l}}} en el lado izquierdo y $${\ displaystyle \ tau = c_ {m} r_ {m}}en el lado derecho. La ecuación del cable ahora se puede escribir en su forma quizás mejor conocida:

$${\ displaystyle \ lambda ^ {2} {\ frac {\ parcial ^ {2} V} {\ parcial x ^ {2}}} = \ tau {\ frac {\ parcial V} {\ parcial t}} + V }

( 20 )

Esta es una ecuación de calor 1D o una ecuación de difusión para la cual se han desarrollado muchos métodos de solución, como las funciones de Green y los métodos de Fourier.

También es un caso especial de la ecuación de Telegrapher .

Figura. 2: capacitancia de la fibra

Cameron Health era un desarrollador de dispositivos médicos con sede en San Clemente , California , EE. UU. Cameron Health tenía su oficina europea, Cameron Health BV, en Arnhem , Países Bajos . El enfoque de la compañía privada se centró en una nueva generación de desfibrilador-cardioversor implantable (ICD) mínimamente invasivo, que llamaron un desfibrilador implantable subcutáneo (S-ICD). El enfoque de Cameron Health evitó la implantación de cables transvenosos en el corazón , que era el procedimiento habitual para los dispositivos cardíacos. En cambio, el ICD de Cameron se implantó por completo fuera de la pared torácica.

En junio de 2012, Boston Scientific adquirió oficialmente Cameron Health por un monto total de $ 1.3 mil millones, que se pagó de manera incremental a medida que se lograron varios hitos de ingresos. ^[1] A partir de febrero de 2016 , Boston Scientific aún comercializa el sistema S-ICD.

Razones para un enfoque mínimamente invasivo [ editar ]

Cada DAI está diseñado para detectar ritmos cardíacos consistentes con una falla catastrófica de la regulación natural del cuerpo del latido cardíaco, que, si no se trata, podría causar la muerte. Cuando un DAI detecta una arritmia grave , emite un impulso eléctrico al músculo cardíaco, de una magnitud suficiente para hacer que el corazón vuelva a un ritmo normal. Los ICD con derivaciones transvenosas administran este choque al interior del músculo cardíaco; El dispositivo Cameron Health generó un shock más poderoso que puede ser efectivo desde fuera del corazón. En opinión de Cameron Health, las derivaciones transvenosas hacia el corazón complicaron innecesariamente el proceso de implantación de un dispositivo y plantearon otros problemas y riesgos que su enfoque menos invasivo evita. ^[3]

El DCI subcutáneo de Cameron Health se encontraba fuera de la caja torácica y no tiene conexión con el interior del corazón. El procedimiento quirúrgico para la implantación fue mínimamente invasivo en comparación con el procedimiento tradicional de enhebrar los cables en el sistema venoso subclavio, a través de la vena cava superior y en una o más áreas endocárdicas del corazón, un procedimiento que a menudo requiere un cardiólogocon capacitación especializada en electrofisiología. . ^[4] Además de los riesgos inherentes a la cirugía cardíaca, los cables también han demostrado ser una debilidad en algunos diseños de ICD. ^[5]Según una estimación, los pacientes con ICD tienen una probabilidad del 20 por ciento de falla de plomo dentro de 10 años, y la sustitución de los cables conlleva un riesgo de muerte de entre dos y cinco por ciento. ^[6] Algunos fabricantes de dispositivos han tenido que reemplazar los cables defectuosos que expusieron a los individuos implantados a choques innecesarios u otros fallos de funcionamiento, en algunos casos, posiblemente resultando en muertes. ^[7] [8]

El S-ICD de Cameron Health tenía la desventaja de ser algo más voluminoso que los ICD existentes. ^[6] Además, este tipo de DAI no incluía un marcapasos, lo que restringía el rango de pacientes para los cuales sería apropiado; se estimó que la mayoría de los pacientes que recibieron implantes de marcapasos / DAI combinados calificarían para un DAI puro. Estos pacientes tendían a tener afecciones genéticas o de otro tipo que los predisponen a una muerte cardíaca súbita debido a una falla del corazón para mantener un ritmo normal. ^[9]

Los ensayos clínicos y aprobaciones [ editar ]

Un ensayo con 53 pacientes, que se implantaron temporalmente con S-ICD, se informó en 2005 en el Congreso de la Sociedad Europea de Cardiología . ^[10] Una segunda serie de 55 pacientes de ensayo se realizó en 2008 y 2009 en 10 centros en Europa y Nueva Zelanda . De los 55 pacientes, 53 tuvieron dos casos de fibrilación y en 52 se convirtieron con éxito. Estos hallazgos se informaron a las autoridades de la Unión Europea en 2009 y dieron como resultado la aprobación para comercializar el dispositivo. Un estudio de 300 pacientes está en progreso para las aprobaciones de los EE. UU. ^[6] [11] En mayo de 2010, se actualizaron, combinaron y publicaron pequeños estudios no aleatorizados de fase temprana destinados principalmente a demostrar la viabilidad de un DAI completamente subcutáneo. En este informe, el sistema detectó y convirtió con éxito y consistentemente episodios de fibrilación ventricular que se indujeron durante las pruebas electrofisiológicas. En el ensayo europeo de 55 pacientes, después de 46 años de seguimiento, 54 de los 55 pacientes estaban vivos y la muerte única se debió a insuficiencia renal. En este ensayo, el sistema detectó y trató con éxito 12 episodios (100%) de taquiarritmia ventricular sostenida espontánea en tres pacientes, antes del inicio del síncope y sin eventos adversos. Uno de los tres pacientes fue tratado exitosamente por siete episodios sucesivos de taquicardia ventricular, una condición conocida como "tormenta de TV".

Financiamiento [ editar ]

Boston Scientific adquirió una opción exclusiva para comprar Cameron Health en 2004 e hizo una inversión de capital no revelada en la compañía en ese momento. ^[12] En 2008, varios inversionistas adicionales organizados por la compañía de inversiones Piper Jaffray ^[13] e incluyendo a PTV Healthcare Capital, Delphi Ventures, Sorrento Ventures, Three Arch Partners y Versant Ventures proporcionaron un poco más de $ 50 millones para financiar el funcionamiento continuo de la compañía. . ^[14]

En junio de 2012, Boston Scientific adquirió oficialmente Cameron Health por un monto total de $ 1.3 mil millones, que se pagó de manera incremental a medida que se lograron varios hitos de ingresos.