MECÁNICA

pandeo es una inestabilidad matemática que conduce a un modo de falla .

Cuando una estructura es sometida a estrés compresivo. , se puede producir pandeo. El pandeo se caracteriza por una repentina desviación lateral de un miembro estructural. Esto puede ocurrir incluso si las tensiones que se desarrollan en la estructura están muy por debajo de las necesarias para provocar el fallo del material del que está compuesta la estructura. A medida que aumenta la carga aplicada en un miembro, como una columna, en última instancia, será lo suficientemente grande como para hacer que el miembro se vuelva inestable y se dice que se ha doblado. La carga adicional causará deformaciones significativas y algo impredecibles, lo que posiblemente lleve a la pérdida completa de la capacidad de carga del miembro. Si las deformaciones que se producen después del pandeo no causan el colapso completo de ese miembro, el miembro continuará soportando la carga que causó que se combara. Si el miembro con hebilla es parte de un conjunto más grande de componentes como un edificio,

En un sentido matemático, el pandeo es una bifurcación en la solución de las ecuaciones del equilibrio estático . En un cierto punto, bajo una carga creciente, cualquier carga adicional se puede sostener en uno de dos estados de equilibrio: un estado puramente comprimido (sin desviación lateral) o un estado de deformación lateral.

Columnas [ editar ]

Una columna bajo una carga axial concéntrica que muestra la deformación característica del pandeo.

La excentricidad de la fuerza axial da como resultado un momento de flexión que actúa sobre el elemento de viga.

La relación de la longitud efectiva de una columna al radio mínimo de giro de su sección transversal se denomina relación de esbeltez (a veces se expresa con la letra griega lambda, λ). Esta relación proporciona un medio para clasificar las columnas y su modo de falla. La relación de esbeltez es importante por consideraciones de diseño. Todos los siguientes son valores aproximados utilizados por conveniencia.

Si la carga en una columna se aplica a través del centro de gravedad(centroide) de su sección transversal, se denomina carga axial . Una carga en cualquier otro punto de la sección transversal se conoce como excéntricacarga. Una columna corta bajo la acción de una carga axial fallará por compresión directa antes de que se doble, pero una columna larga cargada de la misma manera fallará al saltar repentinamente lateralmente (pandeo) en un modo de flexión. El modo de pandeo de la deflexión se considera un modo de falla, y generalmente ocurre antes de que las tensiones de compresión axial (compresión directa) puedan causar la falla del material al ceder o fracturar ese miembro de compresión. Sin embargo, las columnas de longitud intermedia fallarán por una combinación de tensión de compresión directa y flexión.

En particular:

• Una columna de acero corta es aquella cuya relación de esbeltez no excede de 50; una columna de acero de longitud intermedia tiene una relación de esbeltez que oscila entre aproximadamente 50 y 200, y su comportamiento está dominado por el límite de resistencia del material, mientras que una columna de acero larga puede tener una relación de esbeltez mayor que 200 y su comportamiento es dominado Por el módulo de elasticidad del material.
• Una columna de hormigón corta es aquella que tiene una relación de longitud no admitida a dimensión mínima de la sección transversal igual o menor que 10. Si la relación es mayor que 10, se considera una columna larga (a veces denominada columna delgada).
• Las columnas de madera pueden clasificarse como columnas cortas si la relación entre la longitud y la dimensión menor de la sección transversal es igual o menor que 10. La línea divisoria entre columnas de madera intermedias y largas no se puede evaluar fácilmente. Una forma de definir el límite inferior de las columnas de madera largas sería establecerlo como el valor más pequeño de la relación de longitud a área de sección transversal mínima que solo excedería cierta constante K del material. Como K depende del módulo de elasticidad y del esfuerzo compresivo permisible paralelo al grano, se puede ver que este límite arbitrario variaría con las especies de la madera. El valor de K se da en la mayoría de los manuales estructurales.

La teoría del comportamiento de las columnas fue investigada en 1757 por el matemático Leonhard Euler . Derivó la fórmula, la fórmula de Euler, que proporciona la carga axial máxima que una columna larga, delgada e ideal puede soportar sin combarse. Una columna ideal es una que sea perfectamente recta, hecha de un material homogéneo y libre de tensión inicial. Cuando la carga aplicada alcanza la carga de Euler, a veces llamada carga crítica, la columna se encuentra en un estado de equilibrio inestable.. En esa carga, la introducción de la fuerza lateral más leve hará que la columna falle al "saltar" repentinamente a una nueva configuración, y se dice que la columna se ha doblado. Esto es lo que sucede cuando una persona se para en una lata de aluminio vacía y luego toca brevemente los lados, haciendo que se aplaste instantáneamente (los lados verticales de la lata se entienden como una serie infinita de columnas extremadamente delgadas). La fórmula derivada por Euler para columnas largas y delgadas se da a continuación.

$${\ displaystyle F = {\ frac {\ pi ^ {2} EI} {(KL) ^ {2}}}}

Para obtener la demostración matemática lea: Carga crítica de Euler.

dónde

$${\ displaystyle F}, fuerza máxima o crítica (carga vertical sobre columna),

$${\ displaystyle E}, módulo de elasticidad ,

$${\ displaystyle I}, momento de inercia del área más pequeña (segundo momento del área) de la sección transversal de la columna,

$${\ displaystyle L}, longitud de columna no admitida,

$${\ displaystyle K}, factor de longitud efectiva de columna , cuyo valor depende de las condiciones de soporte final de la columna, de la siguiente manera.

Para ambos extremos fijados (con bisagras, libres para girar), $${\ displaystyle K} = 1.0.

Para ambos extremos fijos, $${\ displaystyle K} = 0.50.

Para un extremo fijo y el otro extremo fijado, $${\ displaystyle K}= √ 2 /2 ≈ 0,7071.

Por un extremo fijo y el otro libre para moverse lateralmente, $${\ displaystyle K} = 2.0.

$${\ displaystyle KL} Es la longitud efectiva de la columna.

El examen de esta fórmula revela los siguientes hechos con respecto a la capacidad de carga de las columnas delgadas.

• La elasticidad del material de la columna y no la resistencia a la compresión del material de la columna determina la carga de pandeo de la columna.
• La carga de pandeo es directamente proporcional al segundo momento del área de la sección transversal.
• Las condiciones de contorno tienen un efecto considerable en la carga crítica de columnas delgadas. Las condiciones de contorno determinan el modo de flexión de la columna y la distancia entre los puntos de inflexión en la curva de desplazamiento de la columna desviada. Los puntos de inflexión en la forma de deflexión de la columna son los puntos en los que la curvatura de la columna cambia de signo y también son los puntos en los cuales los momentos de flexión interna de la columna de la columna son cero. Cuanto más cerca estén los puntos de inflexión, mayor será la capacidad de carga axial resultante (carga de movimiento) de la columna.

Un modelo de demostración que ilustra los diferentes modos de pandeo "Euler". El modelo muestra cómo las condiciones de contorno afectan la carga crítica de una columna delgada. Observe que las columnas son idénticas, aparte de las condiciones de contorno.

Una conclusión de lo anterior es que la carga de pandeo de una columna puede aumentarse cambiando su material a uno con un módulo de elasticidad (E) más alto, o cambiando el diseño de la sección transversal de la columna para aumentar su momento de inercia. Esto último se puede hacer sin aumentar el peso de la columna distribuyendo el material tan lejos como sea posible del eje principal de la sección transversal de la columna. Para la mayoría de los propósitos, el uso más efectivo del material de una columna es el de una sección tubular.

Otra idea que se puede extraer de esta ecuación es el efecto de la longitud en la carga crítica. Al duplicar la longitud no admitida de la columna, se acomoda la carga permitida. La restricción ofrecida por las conexiones finales de una columna también afecta su carga crítica. Si las conexiones son perfectamente rígidas (no permite la rotación de sus extremos), la carga crítica será cuatro veces mayor que para una columna similar donde los extremos están sujetos (permitiendo la rotación de sus extremos).

Dado que el radio de giro se define como la raíz cuadrada de la relación del momento de inercia de la columna sobre un eje con respecto a su área de sección transversal, la fórmula de Euler anterior puede reformatearse sustituyendo el radio de giro A · r ² por I:

$${\ displaystyle \ sigma = {\ frac {F} {A}} = {\ frac {\ pi ^ {2} E} {\ left ({\ frac {\ ell} {r}} \ right) ^ {2 }}}}

dónde $${\ displaystyle F / A = \ sigma} es el estrés que causa que la columna se doble, y $${\ displaystyle l / r} es la relación de esbeltez

Dado que las columnas estructurales suelen ser de longitud intermedia, la fórmula de Euler tiene poca aplicación práctica para el diseño normal. Los problemas que causan la desviación del comportamiento puro de la columna de Euler incluyen imperfecciones en la geometría de la columna en combinación con el comportamiento de la tensión de la plasticidad / no lineal del material de la columna. En consecuencia, se han desarrollado varias fórmulas de columnas empíricas que coinciden con los datos de prueba, todos los cuales representan la relación de esbeltez. Debido a la incertidumbre en el comportamiento de las columnas, para el diseño, se introducen factores de seguridad apropiados en estas fórmulas. Una de esas fórmulas es la fórmula de Perry Robertson.que estima la carga crítica de pandeo basada en una curvatura inicial pequeña supuesta, por lo tanto, una excentricidad de la carga axial. La fórmula de Rankine Gordon (llamada así por William John Macquorn Rankiney Perry Hugesworth Gordon (1899 - 1966)) también se basa en resultados experimentales y sugiere que una columna se doblará con una carga F _max dada por:

$${\ displaystyle {\ frac {1} {F _ {\ text {max}}}} = {\ frac {1} {F_ {e}}} + {\ frac {1} {F_ {c}}}}

donde F _e es la carga máxima de Euler y F _c es la carga de compresión máxima. Esta fórmula produce típicamente una estimación conservadora de F _max .

Auto-pandeo [ editar ]

Para obtener la demostración matemática leer: auto-pandeo

Columna vertical, independiente, con densidad. $${\ displaystyle \ rho}, El módulo de Young $${\ displaystyle E}, y área de sección transversal $${\ displaystyle A}, se doblará bajo su propio peso si su altura supera un cierto valor crítico: ^{[1] [2] [3]}

$${\ displaystyle h _ {\ text {crit}} = \ left ({\ frac {9B ^ {2}} {4}} \, {\ frac {EI} {\ rho gA}} \ right) ^ {\ frac {1} {3}}}

donde g es la aceleración debida a la gravedad, I es el segundo momento del área de la sección transversal del haz y B es el primer cero de la función de Bessel del primer tipo de orden −1/3, que es igual a 1.86635086 ...

Pandeo bajo carga muerta a la tracción [ editar ]

Fig.  2: Sistema de viga elástica que muestra el pandeo bajo carga muerta por tracción.

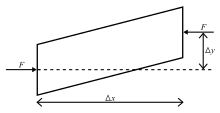
Por lo general, el pandeo y la inestabilidad se asocian con la compresión, pero el pandeo y la inestabilidad también pueden ocurrir en estructuras elásticas sujetas a una carga de tracción máxima . ^[4]

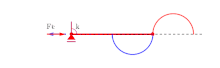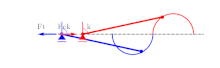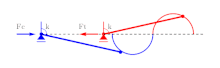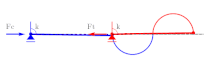
En la Fig.  2 se muestra un ejemplo de una estructura de un solo grado de libertad , donde también se indica la carga crítica. Otro ejemplo que involucra la flexión de una estructura formada por elementos de viga gobernados por la ecuación de la elastica de Euler se muestra en la Fig.  3. En ambos casos, no hay elementos sujetos a compresión. La inestabilidad y el pandeo en tensión están relacionados con la presencia del deslizador, la unión entre las dos varillas, permitiendo solo un deslizamiento relativo entre las piezas conectadas. Mira una película para más detalles.

Restricciones, curvatura y pandeo múltiple [ editar ]

Fig.  3: Una estructura de un grado de libertad que muestra una carga de pandeo a la tracción (compresión) relacionada con el hecho de que el extremo derecho tiene que moverse a lo largo del perfil circular etiquetado Ct(etiquetado Cc ).

El pandeo de una estructura elástica depende en gran medida de la curvatura de las restricciones contra las que se prescriben los extremos de la estructura (ver Bigoni, Misseroni, Noselli y Zaccaria, 2012 ^[5] ). De hecho, incluso un sistema de un solo grado de libertad (ver Fig.  3) puede exhibir una carga de pandeo a la tracción (o compresiva) relacionada con el hecho de que un extremo debe moverse a lo largo del perfil circular etiquetado Ct (etiquetado Cc ).

Fig.  4: Una estructura de un grado de libertad con un perfil bicircular en forma de S que presenta múltiples bifurcaciones (tanto de tracción como de compresión).

Los dos perfiles circulares pueden disponerse en un perfil en forma de 'S', como se muestra en la Fig.  4; en ese caso, se introduce una discontinuidad de la curvatura de la restricción, que conduce a múltiples bifurcaciones. Tenga en cuenta que la estructura de un solo grado de libertad que se muestra en la Fig.  4 tiene dos cargas de pandeo (una de tracción y una de compresión). Mira una película para más detalles.

Inestabilidad Flutter [ editar ]

Las estructuras sujetas a una carga de seguidores (no conservadora) ^{[ aclaración necesaria ]} pueden sufrir inestabilidades que no son del tipo de pandeo y, por lo tanto, no son detectables con un enfoque estático. ^[6]Por ejemplo, la llamada 'columna Ziegler' se muestra en la Fig.  5.

Fig.  5: un boceto de la columna Ziegler , un sistema de dos grados de libertad sujeto a una carga seguidora (la fuerza P permanece siempre paralela a la varilla BC), exhibiendo inestabilidad de aleteo y divergencia. Las dos varillas, de densidad de masa lineal ρ, son rígidas y están conectadas a través de dos resortes giratorios de rigidez k1 y k2.

Este sistema de dos grados de libertad no muestra un pandeo casi estático, pero se vuelve dinámicamente inestable. Para ver esto, notamos que las ecuaciones de movimiento son

${\displaystyle {\begin{aligned}{\frac {1}{3}}\rho l_{1}^{2}\left(l_{1}+3l_{2}\right){\ddot {\alpha }}_{1}+{\frac {1}{2}}\rho l_{1}l_{2}^{2}\cos \left(\alpha _{1}-\alpha _{2}\right){\ddot {\alpha }}_{2}+{\frac {1}{2}}\rho l_{1}l_{2}^{2}\sin \left(\alpha _{1}-\alpha _{2}\right){\dot {\alpha }}_{2}^{2}+{}&\\\left(k_{1}+k_{2}\right)\alpha _{1}-k_{2}\alpha _{2}+\left(\beta _{1}+\beta _{2}\right){\dot {\alpha }}_{1}-\beta _{2}{\dot {\alpha }}_{2}-l_{1}P\sin \left(\alpha _{1}-\alpha _{2}\right)&=0,\\[6pt]{\frac {1}{2}}\rho l_{1}l_{2}^{2}\cos \left(\alpha _{1}-\alpha _{2}\right){\ddot {\alpha }}_{1}+{\frac {1}{3}}\rho l_{2}^{3}{\ddot {\alpha }}_{2}-{\frac {1}{2}}\rho l_{1}l_{2}^{2}\sin \left(\alpha _{1}-\alpha _{2}\right){\dot {\alpha }}_{1}^{2}-{}&\\k_{2}\left(\alpha _{1}-\alpha _{2}\right)-\beta _{2}\left({\dot {\alpha }}_{1}-{\dot {\alpha }}_{2}\right)&=0,\end{aligned}}}$

y su versión linealizada es

{\ displaystyle {\ begin {alineado} {\ frac {1} {3}} \ rho l_ {1} ^ {2} \ left (l_ {1} + 3l_ {2} \ right) {\ ddot {\ alpha }} _ {1} + {\ frac {1} {2}} \ rho l_ {1} l_ {2} ^ {2} {\ ddot {\ alpha}} _ {2} + \ left (k_ {1 } + k_ {2} \ right) \ alpha _ {1} -k_ {2} \ alpha _ {2} -l_ {1} P \ left (\ alpha _ {1} - \ alpha _ {2} \ right ) & = 0, \\ {\ frac {1} {2}} \ rho l_ {1} l_ {2} ^ {2} {\ ddot {\ alpha}} _ {1} + {\ frac {1} {3}} \ rho l_ {2} ^ {3} {\ ddot {\ alpha}} _ {2} -k_ {2} \ left (\ alpha _ {1} - \ alpha _ {2} \ right) & = 0. \ End {alineado}}}

Asumiendo una solución de tiempo-armónico en la forma

$${\ displaystyle \ alpha _ {j} = A_ {j} \, e ^ {- i \ Omega \, t}, ~~~ j = 1,2,}

Encontramos las cargas críticas para flutter ($${\ displaystyle \ P_ {f}}) y divergencia ($${\ displaystyle \ P_ {d}})

$${\ displaystyle P_ {f, d} = {\ frac {k_ {2}} {l_ {1}}} \ cdot {\ frac {k + (1+ \ lambda) ^ {3} \ mp \ lambda \, { \ sqrt {k (3 + 4 \ lambda)}}} {1 + {\ frac {3} {2}} \ lambda}}}

dónde $${\ displaystyle \ lambda = l_ {1} / l_ {2}} y $${\ displaystyle k = k_ {1} / k_ {2}}.

Fig.  6: Una secuencia de formas deformadas en intervalos consecutivos de tiempo de la estructura esbozada en la Fig.  5 y exhibe inestabilidad de aleteo (parte superior) y divergencia (parte inferior).

La inestabilidad del flutter corresponde a un movimiento vibratorio de amplitud creciente y se muestra en la Fig.  6 (parte superior) junto con la inestabilidad de divergencia (parte inferior) que consiste en un crecimiento exponencial.

Recientemente, Bigoni y Noselli (2011) ^[7] han demostrado experimentalmente que las inestabilidades de aleteo y divergencia pueden estar directamente relacionadas con la fricción seca, vea la película para obtener más detalles.

Varias formas de pandeo [ editar ]

El pandeo es un estado que define un punto donde una configuración de equilibrio se vuelve inestable bajo un cambio de carga paramétrico y puede manifestarse en varios fenómenos diferentes. Todos pueden ser clasificados como formas de bifurcación .

Hay cuatro formas básicas de bifurcación asociadas con la pérdida de estabilidad estructural o pandeo en el caso de estructuras con un solo grado de libertad. Estos comprenden dos tipos de bifurcación de la horquilla , una bifurcación de nódulos de silla de montar (a menudo denominada un punto límite ) y una bifurcación transcrítica . Las bifurcaciones de la horquilla son las formas más estudiadas e incluyen el pandeo de columnas, algunas veces conocido como pandeo de Euler; el pandeo de las placas, a veces conocido como pandeo local, que se sabe que es relativamente seguro (ambos son fenómenos supercríticos) y el pandeo de las conchas, que se sabe que es altamente peligroso (fenómeno subcrítico). ^[8]Usando el concepto de energía potencial, el equilibrio se define como un punto estacionario con respecto al grado (s) de libertad de la estructura. Entonces podemos determinar si el equilibrio es estable, como en el caso de que el punto estacionario sea un mínimo local; o inestable, como en el caso en el que el punto estacionario es un punto máximo de inflexión o punto de silla (solo para estructuras de múltiples grados de libertad); consulte las animaciones a continuación.

Modelos de enlace rígido arquetípicos con un solo grado de libertad (SDOF) utilizados para demostrar los fenómenos básicos de pandeo (vea los diagramas de bifurcación a continuación). Todos los casos comienzan en la posición correspondiente a q = 0.

• 

  Braguero con brida de muelle (modelo de arco atado poco profundo).
 
• 

  Eslabón del puntal con resorte giratorio.
 
• 

  Eslabón del puntal con resorte translacional transversal.
• 

  Soporte de enlace asimétrico.

Animaciones de la variación de la energía potencial total (rojo) para varios valores de carga, P (negro), en sistemas estructurales genéricos con el comportamiento de bifurcación o pandeo indicado.

• 

  Dos bifurcaciones de nódulos de silla de montar (puntos límite).
 
• 

  Bifurcación de horquilla supercrítica (punto de pandeo simétrico estable).
 
• 

  Bifurcación de horquilla subcrítica (punto de pandeo inestable-simétrico).
• 

  Bifurcación transcrítica (punto de pandeo asimétrico).

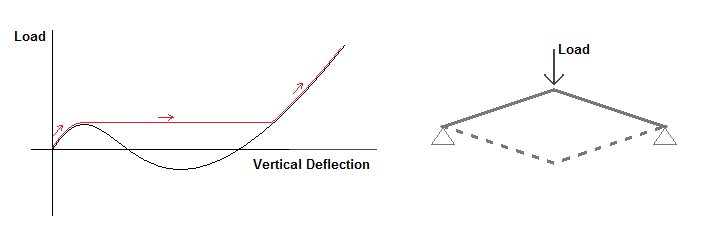
En el pandeo de Euler, ^[9] [10] cuando la carga aplicada se incrementa en una pequeña cantidad más allá de la carga crítica, la estructura se deforma en una configuración de pandeo que es adyacente a la configuración original. Por ejemplo, la columna de Euler que se muestra en la imagen comenzará a inclinarse cuando se carga ligeramente por encima de su carga crítica, pero no se colapsará repentinamente.

En estructuras que experimentan inestabilidad de punto límite, si la carga aumenta infinitamente más allá de la carga crítica, la estructura sufre una gran deformación en una configuración estable diferente que no es adyacente a la configuración original. Un ejemplo de este tipo de pandeo es un marco de palanca (en la imagen) que se "ajusta" a su configuración de pandeo.

Placa de pandeo [ editar ]

Una placa es una estructura tridimensional definida por tener un ancho de tamaño comparable a su longitud, con un espesor que es muy pequeño en comparación con sus otras dos dimensiones. Al igual que las columnas, las placas delgadas experimentan deformaciones de pandeo fuera del plano cuando se las somete a cargas críticas; sin embargo, en contraste con el pandeo de la columna, las placas con cargas de pandeo pueden continuar transportando cargas, llamadas pandeo local. Este fenómeno es increíblemente útil en numerosos sistemas, ya que permite que los sistemas se diseñen para proporcionar mayores capacidades de carga.

Para una placa rectangular, apoyada a lo largo de cada borde, cargada con una fuerza de compresión uniforme por unidad de longitud, la ecuación gobernante derivada se puede establecer mediante: ^[11]

$${\ displaystyle {\ frac {\ parcial ^ {4} w} {\ parcial x ^ {4}}} + {\ frac {\ parcial ^ {4} w} {\ parcial x ^ {2} \ parcial y ^ {2}}} + {\ frac {\ parcial ^ {4} w} {\ parcial y ^ {4}}} = {\ frac {12 \ izquierda (1- \ nu ^ {2} \ derecha)} { Et ^ {3}}} \ left (-N_ {x} {\ frac {\ partial ^ {2} w} {\ partial x ^ {2}}} \ right)}

dónde

$${\ displaystyle w}, desviación fuera del plano

$${\ displaystyle N_ {x}}, carga compresiva distribuida uniformemente

$${\ displaystyle \ nu}, Relación de Poisson

$${\ displaystyle E}, módulo de elasticidad

$${\ displaystyle t}, espesor

La solución a la desviación se puede expandir en dos funciones armónicas que se muestran: ^[11]

$${\ displaystyle w = \ sum _ {m = 1,2,3, \ ldots} \ sum _ {n = 1,2,3, \ ldots} w_ {mn} \ sin \ left ({\ frac {m \ pi x} {a}} \ derecha) \ sin \ izquierda ({\ frac {n \ pi y} {b}} \ derecha)}

dónde

$${\ displaystyle m}, número de curvaturas sinusoidales que ocurren longitudinalmente

$${\ displaystyle n}, número de curvaturas sinusoidales que ocurren a lo ancho

$${\ displaystyle a}, longitud del espécimen

$${\ displaystyle b}ancho del espécimen

La ecuación anterior se puede sustituir en la ecuación diferencial anterior donde $${\ displaystyle n} es igual a 1. $${\ displaystyle N_ {x}}se puede separar proporcionando la ecuación para la carga de compresión crítica de una placa: ^[11]

$${\ displaystyle N_ {x, cr} = k_ {cr} {\ frac {\ pi ^ {2} Et ^ {3}} {12 \ left (1- \ nu ^ {2} \ right) b}}}

dónde

$${\ displaystyle k_ {cr}}, coeficiente de pandeo, dado por: ^[11]

$${\ displaystyle k_ {cr} = \ left ({\ frac {mb} {a}} + {\ frac {a} {mb}} \ right) ^ {2}}

El coeficiente de pandeo está influenciado por el aspecto de la muestra, $${\ displaystyle a} / $${\ displaystyle {b}}, y el número de curvaturas longitudinales. Para un número creciente de dichas curvaturas, la relación de aspecto produce un coeficiente de pandeo variable; pero cada relación proporciona un valor mínimo para cada$${\ displaystyle m}. Este valor mínimo se puede utilizar como una constante, independientemente de la relación de aspecto y$${\ displaystyle m}. ^[11]

Dado que la carga por unidad de área encuentra la tensión, se encuentra la siguiente expresión para la tensión crítica:

$${\ displaystyle \ sigma _ {cr} = k_ {cr} {\ frac {\ pi ^ {2} E} {12 \ left (1- \ nu ^ {2} \ right) \ left ({\ frac {b } {t}} \ derecha) ^ {2}}}}

De las ecuaciones derivadas, se pueden ver las similitudes cercanas entre la tensión crítica para una columna y para una placa. Como el ancho$${\ displaystyle b}se encoge, la placa actúa más como una columna, ya que aumenta la resistencia a doblarse a lo largo del ancho de la placa. El aumento de$${\ displaystyle a}permite un aumento de la cantidad de ondas sinusoidales producidas por el pandeo a lo largo de la longitud, pero también aumenta la resistencia del pandeo a lo largo del ancho. ^[11] Esto crea la preferencia de la placa a doblarse de tal manera que sea igual al número de curvaturas a lo largo del ancho y la longitud. Debido a las condiciones de contorno, cuando una placa se carga con una tensión crítica y se dobla, los bordes perpendiculares a la carga no pueden deformarse fuera del plano y, por lo tanto, continuarán soportando las tensiones. Esto crea una carga de compresión no uniforme a lo largo de los extremos, donde los esfuerzos se imponen en la mitad del ancho efectivo en cada lado de la muestra, dado por lo siguiente: ^[11]

$${\ displaystyle {\ frac {b _ {\ text {eff}}} {b}} = {\ sqrt {{\ frac {\ sigma _ {cr}} {\ sigma _ {y}}} \ left (1- 1.022 {\ sqrt {\ frac {\ sigma _ {cr}} {\ sigma _ {y}}} \ right {}}}}

dónde

$${\ displaystyle b _ {\ text {eff}}}ancho efectivo

$${\ displaystyle \ sigma _ {y}}, produciendo estrés

A medida que aumenta la tensión cargada, el ancho efectivo continúa reduciéndose; Si las tensiones en los extremos alcanzan la tensión de rendimiento, la placa fallará. Esto es lo que permite que la estructura abrochada continúe soportando cargas. Cuando la carga axial sobre la carga crítica se traza contra el desplazamiento, se muestra la trayectoria fundamental. Demuestra la similitud de la placa con una columna en pandeo; sin embargo, más allá de la carga de pandeo, el camino fundamental se bifurca en un camino secundario que se curva hacia arriba, proporcionando la capacidad de ser sometido a cargas más altas más allá de la carga crítica.

Ruedas de bicicleta [ editar ]

Una rueda de bicicleta convencional consiste en una llanta delgada mantenida bajo un alto esfuerzo de compresión por el tirón hacia adentro (aproximadamente normal) de una gran cantidad de radios. Puede considerarse como una columna cargada que se ha doblado en un círculo. Si la tensión del radio aumenta más allá de un nivel seguro, la rueda falla espontáneamente en una forma característica de silla de montar (a veces llamada "taco" o " pringle ") como una columna tridimensional de Euler. Normalmente, esta es una deformación puramente elástica y la llanta recuperará su forma plana adecuada si la tensión del radio se reduce ligeramente.

Materiales de superficie [ editar ]

Vías ferroviarias en los Países Bajos afectadas por Sun kink.

El pandeo también es un modo de falla en materiales de pavimento , principalmente con concreto, ya que el asfalto es más flexible. El calor radiante del sol se absorbe en la superficie de la carretera y hace que se expanda , lo que obliga a las piezas adyacentes a empujarse unas contra otras. Si la tensión es lo suficientemente grande, el pavimento puede levantarse y agrietarse sin previo aviso. Pasar por una sección con hebillas puede ser muy molesto para los conductores de automóviles , que se describe como correr en una joroba de velocidad a velocidades de autopista.

De manera similar, las vías del tren también se expanden cuando se calientan, y pueden fallar al doblarse, un fenómeno llamado pliegue solar . Es más común que los rieles se muevan lateralmente, a menudo arrastrando los lazos subyacentes (durmientes).

Causa [ editar ]

La fuerza de pandeo en la pista debido al calentamiento es solo una función del aumento de temperatura y es independiente de la longitud de la pista:

$${\ displaystyle F = EA \ alpha _ {L} \ Delta T}.

Derivación de la función de la fuerza de pandeo:

La expansión térmica lineal debida al calentamiento de la vía se encuentra utilizando

$${\ displaystyle \ Delta L = \ alpha _ {L} \ Delta T \ L}

dónde

• ΔL, expansión térmica del carril.
• L, longitud del carril / vía
• α, coeficiente de expansión térmica
• ΔT, aumento de temperatura

Según la ley de Hooke, la extensión debida a una fuerza (en el riel) es

$${\ displaystyle \ Delta L = {\ frac {F} {EA}} L}

dónde

• ΔL, extensión del carril / vía
• F, la fuerza que extiende una varilla, aquí la fuerza inducida en el riel.
• E, módulo de elasticidad del material ferroviario (acero)
• A, sección transversal del carril.
• L, longitud del carril

Poner estos juntos da

{\ displaystyle {\ begin {alineado} {\ frac {F} {EA}} L & = \ alpha _ {L} \ Delta T \ L \ Longleftrightarrow \\ F & = EA \ alpha _ {L} \ Delta T \ end {alineado}}}

Accidentes [ editar ]

Estos accidentes se consideraron relacionados con el sol ( más información disponible en la Lista de accidentes ferroviarios (2000-2009) ):

• 18 de abril de 2002 Descarrilamiento del tren automático de Amtrak , fuera de las pistas CSX , cerca de Crescent City, Florida .
• 29 de julio de 2002 Descarrilamiento de Amtrak Capitol Limited , fuera de las pistas de CSX , cerca de Kensington, Maryland .
• 8 de julio de 2010 Descarrilamiento de trenes CSX en Waxhaw, Carolina del Norte .
• 6 de julio de 2012 Descarrilamiento del tren WMATA Metrorail cerca de la estación West Hyattsville , Maryland. ^[12]

Método de energía [ editar ]

A menudo, es muy difícil determinar la carga de pandeo exacta en estructuras complejas con la fórmula de Euler, debido a la dificultad para determinar la constante K. Por lo tanto, la carga de pandeo máxima se suele aproximar utilizando la conservación de energía y se conoce como un método de energía en el análisis estructural .

El primer paso en este método es asumir un modo de desplazamiento y una función que represente ese desplazamiento. Esta función debe satisfacer las condiciones de contorno más importantes, como el desplazamiento y la rotación. Cuanto más precisa sea la función de desplazamiento, más preciso será el resultado.

El método asume que el sistema (la columna) es un sistema conservador en el que la energía no se disipa en forma de calor, por lo tanto, la energía agregada a la columna por las fuerzas externas aplicadas se almacena en la columna en forma de energía de tensión.

$${\ displaystyle U _ {\ text {aplicado}} = U _ {\ text {tensión}}}

En este método, se utilizan dos ecuaciones (para pequeñas deformaciones) para aproximar la energía de "tensión" (la energía potencial almacenada como deformación elástica de la estructura) y la energía "aplicada" (el trabajo realizado en el sistema por fuerzas externas).

{\ displaystyle {\ begin {alineado} U _ {\ text {tensión}} & = {\ frac {E} {2}} \ int I (x) (w_ {xx} (x)) ^ {2} \, dx \\ U _ {\ text {aplicado}} & = {\ frac {P _ {\ text {crit}}} {2}} \ int (w_ {x} (x)) ^ {2} \, dx \ end {alineado}}}

dónde $${\ displaystyle w (x)} Es la función de desplazamiento y los subíndices. $${\ displaystyle x} y $${\ displaystyle xx}Consulte las derivadas primera y segunda del desplazamiento. Conservación de los rendimientos energéticos:

Pandeo flexural-torsional [ editar ]

El pandeo de flexión torsional se puede describir como una combinación de la respuesta de flexión y torsión de un miembro en compresión. Tal modo de desviación debe considerarse para propósitos de diseño. Esto ocurre principalmente en columnas con secciones transversales "abiertas" y, por lo tanto, tienen una rigidez torsional baja, como canales, tees estructurales, formas de doble ángulo y ángulos simples de patas iguales. Las secciones transversales circulares no experimentan tal modo de bucking.

Pandeo lateral-torsional [ editar ]

Pandeo lateral-torsional de una viga en I con fuerza vertical en el centro: a) vista longitudinal, b) sección transversal cerca del soporte, c) sección transversal en el centro con pandeo lateral-torsional

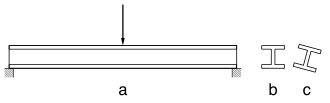
Cuando una viga simplemente soportada se carga en flexión , el lado superior está en compresión y el lado inferior está en tensión . Si la viga no se apoya en la dirección lateral (es decir, perpendicular al plano de flexión), y la carga de flexión aumenta hasta un límite crítico, la viga experimentará una desviación lateral de la brida de compresión cuando se combe localmente. La desviación lateral de la brida de compresión está restringida por la banda de la viga y la brida de tensión, pero para una sección abierta, el modo de torsión es más flexible, por lo que la viga se tuerce y desvía lateralmente en un modo de falla conocido como pandeo lateral-torsional. En las secciones de ala ancha (con una alta rigidez lateral de flexión), el modo de deflexión será principalmente de torsión. En las secciones de brida estrecha, la rigidez a la flexión es menor y la desviación de la columna será más cercana a la del modo de deflexión lateral.

El uso de secciones cerradas, como la sección cuadrada y hueca, mitigará los efectos del pandeo lateral-torsional debido a su alta rigidez torsional .

El factor de modificación ( C _b ) [ editar ]

C _b es un factor de modificación utilizado en la ecuación para la resistencia a la flexión nominal al determinar el pandeo lateral-torsional. La razón de este factor es permitir diagramas de momento no uniformes cuando los extremos de un segmento de viga están reforzados. El valor conservativo para C _b puede tomarse como 1, independientemente de la configuración del haz o la carga, pero en algunos casos puede ser excesivamente conservador. C _b es siempre igual o mayor que 1, nunca menor. Para cantilevers o voladizos donde el extremo libre no está sujetado, C _b es igual a 1. Existen tablas de valores de C _b para vigas simplemente soportadas.

Si no se da un valor apropiado de C _b en las tablas, se puede obtener a través de la siguiente fórmula:

$${\ displaystyle C_ {b} = {\ frac {12.5M _ {\ max}} {2.5M _ {\ max} + 3M_ {A} + 4M_ {B} + 3M_ {C}}}}

dónde

$${\ displaystyle M _ {\ max}}, valor absoluto del momento máximo en el segmento sin apuntalamiento,

$${\ displaystyle M_ {A}}, valor absoluto del momento máximo en el punto cuarto del segmento sin apuntalamiento,

$${\ displaystyle M_ {B}}, valor absoluto del momento máximo en la línea central del segmento sin refuerzo,

$${\ displaystyle M_ {C}}, valor absoluto del momento máximo en el punto de tres cuartos del segmento sin apuntalamiento,

El resultado es el mismo para todos los sistemas de unidades.

Pandeo de plastico [ editar ]

La resistencia de pandeo de un miembro es menor que la resistencia de pandeo elástica de una estructura si el material del miembro se tensa más allá del rango del material elástico y dentro del rango de comportamiento del material no lineal (plástico). Cuando la carga de compresión está cerca de la carga de pandeo, la estructura se doblará significativamente y el material de la columna se desviará de un comportamiento de tensión-deformación lineal. El comportamiento de tensión y tensión de los materiales no es estrictamente lineal, incluso por debajo del punto de elasticidad, por lo tanto, el módulo de elasticidad disminuye a medida que aumenta la tensión, y de manera significativa a medida que las tensiones se aproximan a la resistencia elástica del material. Esta reducción de la rigidez del material reduce la resistencia al pandeo de la estructura y da como resultado una carga más baja que la predicha por el supuesto de comportamiento elástico lineal.

Se puede obtener una aproximación más precisa de la carga de pandeo mediante el uso del módulo de elasticidad tangente, E _t , que es menor que el módulo de elasticidad, en lugar del módulo de elasticidad elástico. La tangente es igual al módulo elástico y luego disminuye más allá del límite proporcional. El módulo de tangente es una línea trazada tangente a la curva de tensión-deformación en un valor particular de deformación (en la sección elástica de la curva de tensión-deformación, el módulo de tangente es igual al módulo elástico). Las parcelas del módulo de elasticidad tangente para una variedad de materiales están disponibles en las referencias estándar.

Pandeo dinámico [ editar ]

Si una columna se carga repentinamente y luego se libera la carga, la columna puede soportar una carga mucho mayor que su carga de pandeo estática (aplicada lentamente). Esto puede suceder en una columna larga, sin soporte, utilizada como un martillo de caída. La duración de la compresión en el extremo del impacto es el tiempo requerido para que una onda de esfuerzo se desplace a lo largo de la columna hacia el otro extremo (libre) y retroceda como una onda de alivio. El pandeo máximo se produce cerca del extremo del impacto en una longitud de onda mucho más corta que la longitud de la varilla, y en un esfuerzo muchas veces el esfuerzo de pandeo de una columna cargada estáticamente. La condición crítica para que la amplitud de pandeo permanezca menos de aproximadamente 25 veces la imperfección de la rectitud de la varilla efectiva en la longitud de onda de la hebilla es

$${\ displaystyle \ sigma L = \ rho c ^ {2} h}

dónde $${\ displaystyle \ sigma} es el impacto del estrés, $${\ displaystyle L} es la longitud de la barra, $${\ displaystyle c} es la velocidad de la onda elástica, y $${\ displaystyle h}Es la dimensión lateral más pequeña de una varilla rectangular. Porque la longitud de onda de la hebilla depende solo de$${\ displaystyle \ sigma} y $${\ displaystyle h}, esta misma fórmula es válida para carcasas cilíndricas delgadas de espesor. $${\ displaystyle h}. ^[13]

Pandeo de conchas cilíndricas finas sujetas a cargas axiales [ editar ]

Las soluciones de la ecuación diferencial de ocho órdenes de Donnell dan los diversos modos de pandeo de un cilindro delgado bajo compresión. Pero este análisis, que está de acuerdo con la teoría de la pequeña desviación, da valores mucho más altos que los que se muestran en los experimentos. Por lo tanto, es habitual encontrar la carga crítica de pandeo para varias estructuras que tienen forma cilíndrica a partir de curvas de diseño empíricamente en las que la carga crítica de pandeo F _cr se representa en función de la relación R / t, donde R es el radio yt es el espesor de El cilindro para varios valores de L / R, L la longitud del cilindro. Si hay recortes en el cilindro, se verán afectadas las cargas críticas de pandeo así como los modos de pandeo previo. La presencia o ausencia de refuerzos de recortes también afectará la carga de pandeo.

Pandeo de tuberías y recipientes a presión sujetos a sobrepresión externa [ editar ]

Las tuberías y los recipientes a presión están sujetos a una sobrepresión externa, causada, por ejemplo, por el enfriamiento con vapor dentro de la tubería y la condensación en agua con la consiguiente caída masiva de presión, riesgo de deformación debido a las tensiones del aro de compresión . Las reglas de diseño para el cálculo del espesor de pared requerido o los anillos de refuerzo se dan en varios códigos de tuberías y recipientes a presión.

Corteza cerebral [ editar ]

Los mecanismos de giro cortical apenas comienzan a entenderse. ^[14] Las fuerzas mecánicas de pandeo debidas a la expansión del tejido cerebral probablemente causan que la superficie cortical se doble. ^[15] Este es un ejemplo de cómo la formación de patrones en la naturaleza también puede tener lugar debido a inestabilidades elásticas ^{[16] en} lugar del mecanismo clásico de reacción-difusión propuesto por primera vez por Alan Turing.