TRIGONOMETRÍA

FUNCIONES TRIGONOMÉTRICAS

las funciones trigonométricas (también llamadas funciones circulares , funciones de ángulo o funciones goniométricas ^[1] [2] ) son funciones de un ángulo . Relacionan los ángulos de un triángulo con las longitudes de sus lados. Las funciones trigonométricas son importantes en el estudio de los triángulos y en el modelado de fenómenos periódicos, entre muchas otras aplicaciones.

Las funciones trigonométricas más familiares son el seno , el coseno y la tangente . En el contexto del círculo de unidad estándar (un círculo con unidad de radio 1), donde un triángulo está formado por un rayo que comienza en el origen y forma un ángulo con el eje x , el seno del ángulo da el componente y ( al contrario del ángulo o la elevación) del triángulo, el coseno da el componente x (el adyacente del ángulo o la carrera), y la función tangente da la pendiente ( componente y dividido por el componente x ). Para ángulos menores a un ángulo recto.Las funciones trigonométricas se definen comúnmente como relaciones de dos lados de un triángulo rectángulo que contiene el ángulo, y sus valores se pueden encontrar en las longitudes de varios segmentos de línea alrededor de un círculo unitario. Las definiciones modernas expresan funciones trigonométricas como series infinitas o como soluciones de ciertas ecuaciones diferenciales , permitiendo la extensión de los argumentos a la recta numérica completa ya los números complejos .

Las funciones trigonométricas tienen una amplia gama de usos que incluyen calcular longitudes y ángulos desconocidos en triángulos (a menudo triángulos rectos). En este uso, las funciones trigonométricas se utilizan, por ejemplo, en navegación, ingeniería y física. Un uso común en la física elemental es resolver un vector en coordenadas cartesianas. Las funciones seno y coseno también se usan comúnmente para modelar fenómenos de función periódica, como las ondas de luz y sonido , la posición y la velocidad de los osciladores armónicos, la intensidad de la luz solar y la duración del día, y las variaciones de temperatura promedio a lo largo del año.

En el uso moderno, hay seis funciones trigonométricas básicas, tabuladas aquí con ecuaciones que las relacionan entre sí. Especialmente en los últimos cuatro, estas relaciones a menudo se toman como las definiciones de esas funciones, pero uno puede definirlas igualmente bien geométricamente, o por otros medios, y luego derivar estas relaciones.

Definiciones de triángulos rectángulos [ editar ]

Arriba: función trigonométrica sin θpara los ángulos seleccionados θ , π - θ , π + θ y 2π - θ en los cuatro cuadrantes. 
Abajo: gráfico de función sinusoidal frente a ángulo. Los ángulos del panel superior están identificados.

Gráfico de las seis funciones trigonométricas y el círculo unitario para un ángulo de 0.7 radianes.

La noción de que debería haber una cierta correspondencia estándar entre las longitudes de los lados de un triángulo y los ángulos del triángulo se produce tan pronto como uno reconoce que triángulos similares mantienen las mismas relaciones entre sus lados. Es decir, para cualquier triángulo similar, la proporción de la hipotenusa (por ejemplo) y otro de los lados sigue siendo la misma. Si la hipotenusa es el doble de larga, también lo son los lados. Son estas relaciones las que expresan las funciones trigonométricas.

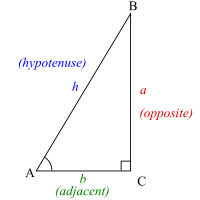
Para definir las funciones trigonométricas para el ángulo A , comenzar con cualquier triángulo rectángulo que contiene el ángulo A . Los tres lados del triángulo se nombran de la siguiente manera:

• La hipotenusa es el lado opuesto al ángulo recto, en este caso el lado h . La hipotenusa es siempre el lado más largo de un triángulo rectángulo.
• El lado opuesto es el lado opuesto al ángulo que nos interesa (ángulo A ), en este caso el lado a .
• El lado adyacente es el lado que tiene los dos ángulos de interés (ángulo A y ángulo recto C ), en este caso el lado b .

En la geometría euclidiana ordinaria , según el postulado del triángulo , los ángulos internos de cada triángulo totalizan 180 ° ( π radianes ). Por lo tanto, en un triángulo rectángulo, los dos ángulos no rectos totalizan 90 ° ( π/2 radianes), por lo que cada uno de estos ángulos debe estar en el rango de (0, π/2 ) como se expresa en la notación de intervalo. Las siguientes definiciones se aplican a los ángulos en este rango (0, π/2 ) . Se pueden extender al conjunto completo de argumentos reales utilizando el círculo unitario., o requiriendo ciertas simetrías y que sean funciones periódicas . Por ejemplo, la figura muestra sin ( θ ) para los ángulos θ , π - θ , π + θ y 2 π - θ representados en el círculo unitario (arriba) y como un gráfico (abajo). El valor del seno se repite aparte del signo en los cuatro cuadrantes, y si el rango de θ se extiende a rotaciones adicionales, este comportamiento se repite periódicamente con un período de 2 π .

Las funciones trigonométricas se resumen en la siguiente tabla y se describen con más detalle a continuación. El ángulo θ es el ángulo entre la hipotenusa y la línea adyacente, el ángulo en A en el diagrama adjunto.

Función	Abreviatura	Descripción	Identidades (utilizando radianes )
seno	pecado	opuesto/hipotenusa	$${\ displaystyle \ sin \ theta = \ cos \ left ({\ frac {\ pi} {2}} - \ theta \ right) = {\ frac {1} {\ csc \ theta}}}
coseno	cos	adyacente/hipotenusa	$${\ displaystyle \ cos \ theta = \ sin \ left ({\ frac {\ pi} {2}} - \ theta \ right) = {\ frac {1} {\ sec \ theta}} \,}
tangente	bronceado (o tg)	opuesto/adyacente	$${\ displaystyle \ tan \ theta = {\ frac {\ sin \ theta} {\ cos \ theta}} = \ cot \ left ({\ frac {\ pi} {2}} - \ theta \ right) = {\ frac {1} {\ cot \ theta}}}
cotangente	cuna (o cotan o cotg o ctg o ctn)	adyacente/opuesto	$${\ displaystyle \ cot \ theta = {\ frac {\ cos \ theta} {\ sin \ theta}} = \ tan \ left ({\ frac {\ pi} {2}} - \ theta \ right) = {\ frac {1} {\ tan \ theta}}}
secante	segundo	hipotenusa/adyacente	$${\ displaystyle \ sec \ theta = \ csc \ left ({\ frac {\ pi} {2}} - \ theta \ right) = {\ frac {1} {\ cos \ theta}}}
cosecante	csc (o cosec)	hipotenusa/opuesto	$${\ displaystyle \ csc \ theta = \ sec \ left ({\ frac {\ pi} {2}} - \ theta \ right) = {\ frac {1} {\ sin \ theta}}}

Seno, coseno y tangente [ editar ]

El seno de un ángulo es la relación entre la longitud del lado opuesto y la longitud de la hipotenusa. La palabra viene del seno latino para golfo o bahía, ^[3] ya que, dado un círculo unitario, es el lado del triángulo en el que se abre el ángulo . En nuestro caso:

$${\ displaystyle \ sin A = {\ frac {\ textrm {opuesto}} {\ textrm {hypotenuse}}}}

Una ilustración de la relación entre el seno y su complemento fuera de fase , el coseno. Coseno es idéntico, pero π/2 radianes fuera de fase a la izquierda; entonces cos A = pecado ( A + π/2 ) .

El coseno ( complemento sinusoidal , latín: coseno , sinusal complementario ) de un ángulo es la relación entre la longitud del lado adyacente y la longitud de la hipotenusa, llamada así porque es el seno del complemento o co-ángulo, la otra ángulo no recto. ^[4] Debido a que la suma de ángulos de un triángulo es π radianes , el ángulo de inclinación B es igual a π/2 - A ; entonces cos A = pecado B = pecado ( π/2 - A ) . En nuestro caso:

$${\ displaystyle \ cos A = {\ frac {\ textrm {adyacente}} {\ textrm {hypotenuse}}}}

La tangente de un ángulo es la relación entre la longitud del lado opuesto y la longitud del lado adyacente, llamada así porque se puede representar como un segmento de línea tangente al círculo, es decir, la línea que toca el círculo, desde la línealatina. Líneas tangentes o de contacto (cf. tangere , al tacto). ^[5] En nuestro caso:

$${\ displaystyle \ tan A = {\ frac {\ textrm {opuesto}} {\ textrm {adyacente}}}}

La tangente también puede representarse en términos de seno y coseno. Es decir:

$${\ displaystyle \ tan A = {\ frac {\ sin A} {\ cos A}} = {\ frac {\ frac {\ textrm {opuesto}} {\ textrm {hypotenuse}}} {\ frac {\ textrm { adyacente}} {\ textrm {hipotenusa}}}} = {\ frac {\ textrm {opuesto}} {\ textrm {adyacente}}}}

Estas proporciones no dependen del tamaño del triángulo rectángulo particular elegido, siempre que el ángulo de enfoque sea igual, ya que todos los triángulos son similares .

Las siglas "SOH-CAH-TOA" ("soak-a-toe", "sock-a-toa", "so-kah-toa") y "OHSAHCOAT" se utilizan comúnmente como nemotécnicas trigonométricas para estas proporciones .

Secante, cosecante y cotangente [ editar ]

Las tres funciones restantes se definen mejor utilizando las tres funciones anteriores y pueden considerarse sus recíprocos .

La secante de un ángulo es el recíproco de su coseno, es decir, la relación entre la longitud de la hipotenusa y la longitud del lado adyacente, llamada así porque representa la línea secante que corta el círculo (del latín: secare, a corte): ^[6]

$${\ displaystyle \ sec A = {\ frac {1} {\ cos A}} = {\ frac {\ textrm {hypotenuse}} {\ textrm {adyacente}}} = {\ frac {h} {b}}. }

La cosecante ( complemento secante , latín: cosecans , secans complementi ) de un ángulo es el recíproco de su seno, es decir, la relación de la longitud de la hipotenusa a la longitud del lado opuesto, llamada así porque es la secante de El complementario o co-ángulo:

$${\ displaystyle \ csc A = {\ frac {1} {\ sin A}} = {\ frac {\ textrm {hypotenuse}} {\ textrm {opuesto}}} = {\ frac {h} {a}}. }

La cotangente ( complemento tangente , latín: cotangens , tangens complementi ) de un ángulo es el recíproco de su tangente, es decir, la relación de la longitud del lado adyacente a la longitud del lado opuesto, llamada así porque es la tangente del complementario o co-ángulo:

$${\ displaystyle \ cot A = {\ frac {1} {\ tan A}} = {\ frac {\ textrm {adyacente}} {\ textrm {opuesto}}} = {\ frac {b} {a}}. }

Mnemonia [ editar ]

Equivalente a las definiciones del triángulo rectángulo, las funciones trigonométricas también se pueden definir en términos de aumento , recorrido y pendiente de un segmento de línea en relación con la horizontal. La pendiente se enseña comúnmente como "subida en carrera" o subida/carrera . Las tres funciones trigonométricas principales se enseñan comúnmente en el orden seno, coseno y tangente. Con una longitud de segmento de línea de 1 (como en un círculo unitario ), los siguientes dispositivos mnemónicos muestran la correspondencia de las definiciones:

1. "Sine is first, rise is first", lo que significa que Sine toma el ángulo del segmento de línea y le dice a su aumento vertical cuando la longitud de la línea es 1.
2. "Cosine está en segundo lugar, ejecutar es segundo", lo que significa que Cosine toma el ángulo del segmento de línea y le dice a su ejecución horizontal cuando la longitud de la línea es 1.
3. "Tangente combina la subida y la carrera", lo que significa que la tangente toma el ángulo del segmento de línea y le indica su pendiente, o alternativamente, indica la subida vertical cuando la carrera horizontal del segmento de línea es 1.

Esto muestra el uso principal de tangente y arctangente: la conversión entre las dos formas de decir la inclinación de una línea, es decir, los ángulos y las pendientes. (La tangente o tangente inversa no debe confundirse con la cotangente , que es coseno dividido por seno).

Mientras que la longitud del segmento de línea no hace ninguna diferencia para la pendiente (la pendiente no depende de la longitud de la línea inclinada), sí afecta la subida y la carrera. Para ajustar y encontrar el aumento real y la carrera cuando la línea no tiene una longitud de 1, simplemente multiplique el seno y el coseno por la longitud de la línea. Por ejemplo, si el segmento de línea tiene la longitud 5, el recorrido en un ángulo de 7 ° es 5cos (7 °).

Definiciones unidad de círculo [ editar ]

En esta ilustración, las seis funciones trigonométricas de un ángulo arbitrario θ se representan como coordenadas cartesianas de puntos relacionados con el círculo unitario . Las ordenadas de A , B y D son pecado θ , tan θ y csc θ, respectivamente, mientras que las abscisas de A , C y E son cos θ , cuna θ y sec θ , respectivamente.

Signos de funciones trigonométricas en cada cuadrante. El nemotécnico " todo s cience t eachers (son) c razy" lista las funciones que son positivos de los cuadrantes I a IV. ^[7] Esta es una variación de la mnemotécnica " Todos los estudiantes toman el cálculo ".

Las seis funciones trigonométricas se pueden definir como valores de coordenadas de puntos en el plano euclidianoque están relacionados con el círculo unitario , que es el círculo de radio centrado en el origen O de este sistema de coordenadas. Mientras que las definiciones de triángulos rectángulos permiten la definición de las funciones trigonométricas para ángulos entre 0 y$${\ displaystyle {\ tfrac {\ pi} {2}}} Radián (90 °), las definiciones del círculo unitario permiten extender el dominiode las funciones trigonométricas a todos los números reales positivos y negativos.

Girando un rayo desde la dirección de la mitad positiva del eje x en un ángulo θ (en sentido contrario a las agujas del reloj para{\ displaystyle \ theta> 0,} y en el sentido de las agujas del reloj para {\ displaystyle \ theta <0 font="">) produce puntos de intersección de este rayo (ver la figura) con el círculo unitario :$${\ displaystyle \ mathrm {A} = (x _ {\ mathrm {A}}, y _ {\ mathrm {A}})}, y, extendiendo el rayo a una línea si es necesario, con la línea$${\ displaystyle {\ text {“}} x = 1 {\ text {”}}: \; \ mathrm {B} = (x _ {\ mathrm {B}}, y _ {\ mathrm {B}}),}y con la linea$${\ displaystyle {\ text {“}} y = 1 {\ text {”}}: \; \ mathrm {C} = (x _ {\ mathrm {C}}, y _ {\ mathrm {C}}).}La línea tangente al círculo unitario en el punto A , que es ortogonal a este rayo, intersecta el eje y - y x en los puntos$${\ displaystyle \ mathrm {D} = (0, y _ {\ mathrm {D}})} y $${\ displaystyle \ mathrm {E} = (x _ {\ mathrm {E}}, 0)}. Los valores de coordenadas de estos puntos dan todos los valores existentes de las funciones trigonométricas para valores reales arbitrarios de θ de la siguiente manera.

Las funciones trigonométricas cos y sin se definen, respectivamente, como los valores de coordenadas x e y del punto A , es decir,

$${\ displaystyle \ cos (\ theta) = x _ {\ mathrm {A}} \ quad} y $${\ displaystyle \ quad \ sin (\ theta) = y _ {\ mathrm {A}}.}^[8]

En el rango $${\ displaystyle 0 \ leq \ theta \ leq \ pi / 2}esta definición coincide con la definición del triángulo rectángulo, al tomar el triángulo rectángulo para tener la unidad de radio OA como hipotenusa , y ya que para todos los puntos$${\ displaystyle \ mathrm {P} = (x, y)} en la unidad circula la ecuación $${\ displaystyle x ^ {2} + y ^ {2} = 1}sostiene, esta definición de coseno y seno también satisface la identidad pitagórica

$${\ displaystyle \ cos ^ {2} \ theta + \ sin ^ {2} \ theta = 1.}

Las otras funciones trigonométricas se pueden encontrar a lo largo del círculo unitario como

$${\ displaystyle \ tan (\ theta) = y _ {\ mathrm {B}} \ quad} y $${\ displaystyle \ quad \ cot (\ theta) = x _ {\ mathrm {C}},}

$${\ displaystyle \ csc (\ theta) \ = y _ {\ mathrm {D}} \ quad} y $${\ displaystyle \ quad \ sec (\ theta) = x _ {\ mathrm {E}}.}

Al aplicar la identidad pitagórica y los métodos de prueba geométrica, se puede demostrar fácilmente que estas definiciones coinciden con las definiciones de tangente, cotangente, secante y cosecante en términos de seno y coseno, es decir

$${\ displaystyle \ tan \ theta = {\ frac {\ sin \ theta} {\ cos \ theta}}, \ quad \ cot \ theta = {\ frac {\ cos \ theta} {\ sin \ theta}}, \ quad \ sec \ theta = {\ frac {1} {\ cos \ theta}}, \ quad \ csc \ theta = {\ frac {1} {\ sin \ theta}}.}

Funciones trigonométricas: seno , coseno , tangente , cosecante (punteado) , secante (punteado), cotangente (punteado)

Como una rotación de un ángulo de $${\ displaystyle \ pm 2 \ pi}no cambia la posición o el tamaño de una forma, los puntos A , B , C , Dy E son los mismos para dos ángulos cuya diferencia es un múltiplo entero de$${\ displaystyle 2 \ pi}. Así, las funciones trigonométricas son funciones periódicas con punto.$${\ displaystyle 2 \ pi}. Es decir, las igualdades.

$${\ displaystyle \ sin \ theta = \ sin \ left (\ theta + 2k \ pi \ right) \ quad} y $${\ displaystyle \ quad \ cos \ theta = \ cos \ left (\ theta + 2k \ pi \ right)}

mantener para cualquier ángulo θ y cualquier entero k . Lo mismo es cierto para las otras cuatro funciones trigonométricas. Observar el signo y la monotonicidad de las funciones seno, coseno, cosecante y secante en los cuatro cuadrantes, muestra que 2 π es el valor más pequeño para el cual son periódicos, es decir, 2 π es el período fundamental de estas funciones. Sin embargo, ya después de una rotación por un ángulo$${\ displaystyle \ pi}los puntos B y C vuelven a su posición original, de modo que la función tangente y la función cotangente tienen un período fundamental de π . Es decir, las igualdades.

$${\ displaystyle \ tan \ theta = \ tan (\ theta + k \ pi) \ quad} y $${\ displaystyle \ quad \ cot \ theta = \ cot (\ theta + k \ pi)}

mantener para cualquier ángulo θ y cualquier entero k .