TRIGONOMETRÍA

Para la compañía de telecomunicaciones llamada Equant, ver Equant (France Télécom) .

Los elementos básicos de la astronomía ptolemaica , que muestran un planeta en un epiciclo (círculo discontinuo más pequeño), un deferente (círculo discontinuo más grande), la excéntrica (×) y un ecuador (•).

Equant (o punctum aequans ) es un concepto matemáticodesarrollado por Claudio Ptolomeo en el siglo II dC para explicar el movimiento observado de los planetas. El ecuador se utiliza para explicar el cambio de velocidad observado en la órbita planetaria durante las diferentes etapas de la órbita. Este concepto planetario permitió a Tolomeo mantener viva la teoría del movimiento circular uniforme al afirmar que el camino de los cuerpos celestes era uniforme alrededor de un punto y circular alrededor de otro punto.

Colocación [ editar ]

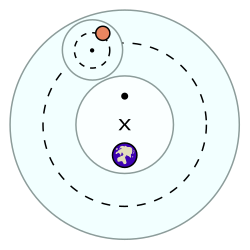
El punto equant (que se muestra en el diagrama con el • grande), se coloca de modo que esté directamente opuesto a la Tierra desde el centro del deferente , conocido como el excéntrico (representado por el ×). Un planeta o el centro de un epiciclo (un círculo más pequeño que lleva el planeta) fue concebido para moverse a una velocidad angular constante con respecto al ecuador. En otras palabras, para un observador hipotético colocado en el punto equante, el centro del epiciclo (indicado por el pequeño ·) parecería moverse a una velocidad angular constante. Sin embargo, el centro del epiciclo no se moverá a una velocidad constante a lo largo de su deferente. ^[1]

El motivo de la implementación del ecuador fue mantener una apariencia de movimiento circular constante de cuerpos celestes , un artículo de fe de larga data originado por Aristóteles por razones filosóficas, al tiempo que permite la mejor coincidencia de los cálculos de los movimientos observados de los cuerpos, particularmente en el tamaño del movimiento retrógrado aparente de todos los cuerpos del Sistema Solar excepto el Sol y la Luna .

Ecuación [ editar ]

El ángulo α cuyo vértice está en el centro del deferente y cuyos lados intersectan el planeta y el ecuador respectivamente es una función del tiempo  t :

$${\ displaystyle \ alpha (t) = \ Omega t- \ arcsin \ left ({\ frac {E} {R}} \ sin (\ Omega t) \ right)}

donde Ω es la velocidad angular constante visto desde el equant que está situado a una distancia E cuando el radio del deferente es  R . ^[2]

El modelo equant tiene un cuerpo en movimiento en un camino circular que no comparte un centro con la Tierra. La velocidad del objeto en movimiento realmente variará durante su órbita alrededor del círculo exterior (línea discontinua), más rápido en la mitad inferior y más lento en la mitad superior. El movimiento se considera uniforme solo porque el planeta se desplaza alrededor de ángulos iguales en tiempos iguales desde el punto equivalente. La velocidad del objeto no es uniforme cuando se ve desde cualquier otro punto dentro de la órbita.

Descubrimiento y uso [ editar ]

Ptolomeo introdujo el ecuador en " Almagesto ". La evidencia de que el ecuador era un ajuste requerido a la física aristotélica se basaba en observaciones hechas por él mismo y cierto "Theon" (quizás, Theon of Smyrna ). ^[1]

En los modelos del universo que preceden a Ptolomeo, generalmente atribuidos a Hipparco , los excéntricos y los epiciclos ya eran una característica. El romano Plinio en el siglo I d. C., que aparentemente tuvo acceso a los escritos de los astrónomos griegos tardíos, y no siendo un astrónomo, identificó correctamente las líneas de ábside de los cinco planetas conocidos y su ubicación en el zodiaco. ^[3] Dichos datos requieren el concepto de centros de movimiento excéntricos. La mayor parte de lo que sabemos sobre Hiparco nos llega a través de menciones de sus obras de Ptolomeo en el Almagesto.. Las características de los "modelos" de Hipparchus explicaron las diferencias en la duración de las estaciones en la Tierra (conocida como la "primera anomalía"), y la aparición de movimiento retrógrado en los planetas (conocida como la "segunda anomalía"). Pero Hiparco no pudo hacer que las predicciones sobre la ubicación y la duración de los movimientos retrógrados de los planetas coincidieran con las observaciones; podría coincidir con la ubicación, o podría coincidir con la duración, pero no ambas simultáneamente. ^[4] La introducción del ecuante por parte de Ptolomeo resolvió esa contradicción: la ubicación se determinó mediante el deferente y el epiciclo, mientras que la duración se determinó mediante un movimiento uniforme alrededor del ecuador.

El modelo de astronomía de Ptolomeo se usó como un método técnico que podía responder preguntas relacionadas con la astrología y predecir las posiciones de los planetas durante casi 1500 años, a pesar de que el equant y el excéntrico eran violaciones de la física aristotélica pura que requería que todo movimiento estuviera centrado en la Tierra. Durante muchos siglos, la rectificación de estas violaciones fue una preocupación de los estudiosos, que culminó en las soluciones de Ibn al-Shatir y Copérnico . Las predicciones de Ptolomeo, que requerían una supervisión y correcciones constantes por parte de los estudiosos interesados ​​durante esos siglos, culminaron en las observaciones de Tycho Brahe en Uraniborg .

No fue hasta que Johannes Kepler publicó su Astronomia Nova , basada en los datos que él y Tycho recolectaron en Uraniborg, que el modelo de los cielos de Ptolomeo fue suplantado por completo por un nuevo modelo geométrico. ^[5] [6]

La crítica [ editar ]

El ecuante resolvió el último gran problema de tener en cuenta el movimiento anómalo de los planetas, pero algunos creyeron que comprometía los principios de los antiguos filósofos / astrónomos griegos, a saber, el movimiento circular uniforme sobre la Tierra. ^[7] En general, se asumió que la uniformidad se observaba desde el centro del deferente, y como eso sucede en un solo punto, solo se observa un movimiento no uniforme desde cualquier otro punto. Ptolomeo movió el punto de observación explícitamente del centro del deferente al ecuante. Esto puede verse como una ruptura de parte de las reglas de movimiento circular uniforme. Los críticos destacados del ecuador incluyen al astrónomo persa Nasir al-Din Tusi, quien desarrolló la pareja Tusi como una explicación alternativa, ^[8] yNicolaus Copernicus , cuya alternativa era un nuevo par de epiciclos para cada deferente. La aversión al ecuador fue una de las principales motivaciones de Copérnico para construir su sistema heliocéntrico. ^[9] [10] Esta violación del movimiento circular perfecto alrededor del centro del deferente molestó a muchos pensadores, especialmente a Copérnico, quien menciona al ecuante como una construcción monstruosa en De Revolutionibus . El movimiento de Copernico de la Tierra lejos del centro del universo evitó la necesidad primaria de los epiciclos de Ptolomeo al explicar el movimiento retrógrado como una ilusión óptica, pero reincorporó dos epiciclos más pequeños en el movimiento de cada planeta para reemplazar el ecuador.

 estimación de los parámetros de la señal mediante técnicas invariantes de rotación (ESPRIT) es una técnica para determinar los parámetros de una mezcla de sinusoides en un ruido de fondo.

El ejemplo de separación en subarrays (2D ESPRIT).

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

La "elipticidad" redirige aquí. Para la elipticidad en el cálculo diferencial, ver operador elíptico . Para otras aplicaciones, vea Aplanamiento (desambiguación) .

Un círculo de un radio de uncomprimido a una elipse.

Una esfera de radio uncomprime a un elipsoide achatado de revolución.

El aplanamiento es una medida de la compresión de un círculo o esfera a lo largo de un diámetro para formar una elipse o un elipsoide de revolución ( esferoide ) respectivamente. Otros términos utilizados son elipticidad u oblatenidad . La notación habitual para el aplanamiento es f y su definición en términos de los semiejes de la elipse o elipsoide resultante es

$${\ displaystyle \ mathrm {aplanamiento} = f = {\ frac {ab} {a}}.

El factor de compresión es b / a en cada caso. Para la elipse, este factor es también la relación de aspecto de la elipse.

Existen otras dos variantes de aplanamiento (ver más abajo) y cuando es necesario evitar la confusión, el aplanamiento anterior se denomina primer aplanamiento . Las siguientes definiciones se pueden encontrar en los textos estándar ^{[1] [2] [3]} y en los textos web en línea .

Definiciones de aplanamiento [ editar ]

A continuación, a es la dimensión más grande (por ejemplo, eje semimayor), mientras que b es la más pequeña (eje semiminor). Todos los acoplamientos son cero para un círculo ( a  =  b ).

(primero) aplanamiento	$${\ displaystyle f \, \!}	$${\ displaystyle {\ frac {ab} {a}} \, \!}	Fundamental. Los elipsoides de referencia geodésicos se especifican dando$${\ displaystyle 1 / f \, \!}
segundo aplanamiento	$${\ displaystyle f '\, \!}	$${\ displaystyle {\ frac {ab} {b}} \, \!}	Raramente usado.
tercer aplanamiento	$${\ displaystyle n, \ quad (f '') \, \!}	$${\ displaystyle {\ frac {ab} {a + b}} \, \!}	Se utiliza en cálculos geodésicos como un pequeño parámetro de expansión. [6]

Identidades que implican aplanamiento [ editar ]

Los aplanamientos están relacionados con otros parámetros de la elipse. Por ejemplo:

{\ displaystyle {\ begin {alineado} b & = a (1-f) = a \ left ({\ frac {1-n} {1 + n}} \ right), \\ e ^ {2} & = 2f -f ^ {2} = {\ frac {4n} {(1 + n) ^ {2}}}. \\ end {alineado}}}

dónde $${\ displaystyle e}Es la excentricidad .

Valores numericos para planetas [ editar ]

Para el elipsoide WGS84 para modelar la Tierra , los valores que definen son ^[7]

a (radio ecuatorial): 6 378 137.0 m

1 / f (aplanamiento inverso): 298.257 223 563

de la cual se deriva

b (radio polar): 6 356 752.3142 m,

de modo que la diferencia entre los semiejes mayor y menor es de 21.385 km (13 mi). (Esto es solo un 0,335% del eje principal, por lo que una representación de la Tierra en una pantalla de computadora tendría un tamaño de 300px por 299px. Debido a que esto sería virtualmente indistinguible de una esfera que se muestra como 300px por 300px, las ilustraciones generalmente exageran enormemente el aplanamiento). casos en los que la imagen debe representar la oblatenidad de la Tierra.)

Otros valores en el Sistema Solar son Jupiter ,   f  = 1/16; Saturno ,   f  = 1/10, la Luna  f  = 1/900. El aplanamiento del Sol es de aproximadamente 9 × 10 ⁻⁶ .

Origen del aplanamiento [ editar ]

En 1687, Isaac Newton publicó los Principia en los que incluyó una prueba de que un cuerpo de fluido autoligitado en equilibrio toma la forma de un elipsoide de revolución oblato (un esferoide ). ^[8] La cantidad de aplanamiento depende de la densidad y el equilibrio de la fuerza gravitacional y la fuerza centrífuga .

La trigonometría ordinaria estudia los triángulos en el plano euclidiano R ² . Hay un número de maneras de definir los ordinarios geométricas euclidianas funciones trigonométricas en números reales : las definiciones triángulo rectángulo- , definiciones de unidad de círculo , las definiciones de la serie , las definiciones a través de ecuaciones diferenciales , las definiciones utilizando ecuaciones funcionales . Generalizaciones de funciones trigonométricas.a menudo se desarrollan comenzando con uno de los métodos anteriores y adaptándolo a una situación distinta de los números reales de la geometría euclidiana. Generalmente, la trigonometría puede ser el estudio de triples de puntos en cualquier tipo de geometría o espacio . Un triángulo es el polígono con el número más pequeño de vértices, por lo que una dirección para generalizar es estudiar análogos de ángulos y polígonos de dimensiones más altas: ángulos sólidos y polítopos tales como tetraedros y n-simples .

Trigonometría [ editar ]

• En la trigonometría esférica , se estudian los triángulos en la superficie de una esfera. Las identidades del triángulo esférico se escriben en términos de las funciones trigonométricas ordinarias, pero difieren de las identidades del triángulo plano .
• Trigonometría hiperbólica
  1. Estudio de triángulos hiperbólicos en geometría hiperbólica con funciones hiperbólicas .
  2. Funciones hiperbólicas en la geometría euclidiana: el círculo unitario está parametrizado por (cos  t , sen  t ) mientras que la hipérbola equilátera está parametrizada por los puntos (cosh  t , sinh  t ).
  3. Girotrigonometría : una forma de trigonometría utilizada en el enfoque del espacio gyrovector a la geometría hiperbólica , con aplicaciones a la relatividad especial y el cálculo cuántico .
  4. La trigonometría hiperbólica universal ^[1] : un enfoque algebraico basado en la trigonometría racional .
• La trigonometría racional : una reformulación de la trigonometría en términos de propagación y cuadratura enlugar de ángulo y longitud .
• Trigonometría para la geometría del taxi ^[2]
• Trigonometrías espaciotemporales ^[3]

• Trigometría cualitativa difusa ^[4]
• Operador de trigonometría ^[5]
• Tridometría de celosía ^[6]

• Trigonometría en espacios simétricos ^{[7] [8] [9]}

Dimensiones superiores [ editar ]

• Seno polar
• Trigonometría de un tetraedro ^[10]
  • Una ley de senos para tetraedros.
• Simplex con una "esquina ortogonal" - Teoremas de Pitágoras para n-simplexes
  • Teorema de De Gua : un teorema de Pitágoras para un tetraedro con una esquina de cubo.

Funciones trigonométricas [ editar ]

• Las funciones trigonométricas se pueden definir para ecuaciones diferenciales fraccionarias . ^[11]

• En el cálculo de escala de tiempo , las ecuaciones diferenciales y las ecuaciones de diferencia se unifican en ecuaciones dinámicas en escalas de tiempo que también incluye ecuaciones de diferencia q . Las funciones trigonométricas se pueden definir en una escala de tiempo arbitraria (un subconjunto de los números reales).
• Las definiciones de serie de sin y cos definen estas funciones en cualquier álgebra en la que converjan series como números complejos , números p-adic , matrices y varias álgebras de Banach .