TRIGONOMETRÍA

La trigonometría racional es una propuesta de reformulación de geometrías planas y sólidas métricas (que incluye trigonometría ) por el matemático canadiense Norman J. Wildberger, actualmente profesor de matemáticas en la Universidad de Nueva Gales del Sur . Sus ideas se exponen en su libro de 2005 Divine Proportions: Rational Trigonometry to Universal Geometry . ^[1] Según New Scientist , parte de su motivación para una alternativa a la trigonometría tradicional era evitar algunos problemas que, según afirma, ocurren cuando se usan series infinitas en matemáticas. La trigonometría racional evita el uso directo de funciones trascendentalesComo el seno y el coseno sustituyendo sus equivalentes cuadrados. ^[2] Wildberger se inspira en los matemáticos anteriores a Georg Cantor 's juego-teoría infinita , como Gauss y Euclides , quien dice eran mucho más cuidado con el uso de los conjuntos infinitos que los matemáticos modernos. ^{[2] [nb 1]} Hasta la fecha, la trigonometría racional no se menciona en gran medida en la literatura matemática general.

Enfoque

La trigonometría racional sigue un enfoque basado en los métodos del álgebra lineal para los temas de geometría elemental (nivel de escuela secundaria). La distancia se reemplaza con su valor cuadrado ( cuadratura ) y el ' ángulo ' se reemplaza con el valor cuadrado de la relación sinusoidal habitual ( dispersión ) asociada a cualquiera de los ángulos entre dos líneas. (El complemento de Spread, conocido como cruz , también corresponde a una forma escalada del producto interno entre segmentos de línea tomados como vectores ). Las tres leyes principales de la trigonometría: el teorema de Pitágoras , la ley sinusoidal.y la ley del coseno : se dan en forma racional (equivalente al cuadrado) y se ven aumentadas por otras dos leyes: la fórmuladel triple cuádruple (que relaciona los cuadriláteros de tres puntos colineales) y la fórmula del triple esparcimiento(que relaciona los diferenciales de tres líneas concurrentes ) -, dando las cinco principales leyes del sujeto. ^{[ cita requerida ]}

La trigonometría racional se basa ampliamente en la geometría analítica cartesiana, con un punto definido como un par ordenado de números racionales

$${\ displaystyle (x, y)}

y una linea

$${\ displaystyle ax + by + c = 0,}

como general ecuación lineal con coeficientes racionales un , b y c .

Al evitar los cálculos que se basan en operaciones de raíz cuadrada que brindan solo distancias aproximadasentre puntos, o funciones trigonométricas estándar (y sus inversos), brindando solo aproximaciones polinómicastruncadas de ángulos (o sus proyecciones), la geometría se vuelve completamente algebraica. En otras palabras, no se asume la existencia de soluciones de problemas de números reales , sino que se obtienen resultados sobre el campo de los números racionales, sus extensiones de campos algebraicos o campos finitos . Siguiendo esto, se afirma, hace que muchos resultados clásicos de la geometría euclidiana sean aplicables en forma racional.Forma (como análogos cuadráticos) sobre cualquier campo que no sea de la característica dos. ^{[ cita requerida ]}

El libro Proporciones divinas muestra la aplicación del cálculo utilizando funciones trigonométricas racionales, incluidos los cálculos de volumen tridimensionales. También se ocupa de la aplicación de la trigonometría racional a situaciones que involucran irracionales, como la prueba de que los Sólidos Platónicos tienen "propagaciones" racionales entre sus caras. ^{[nb 2]}

Notabilidad y crítica.

La trigonometría racional ( RT ) se menciona solo en un número modesto de publicaciones matemáticas, además de los propios artículos y libros de Wildberger. Divine Proportions fue desestimado por el revisor Paul J. Campbell, en la Revista de Matemáticas de la Mathematical Association of America (MAA): "el autor afirma que esta nueva teoría tardará" menos de la mitad del tiempo habitual en aprender ", pero lo dudo. . y aún tendría que estar interconectado con los conceptos tradicionales y la notación ". El crítico William Barker, profesor de matemáticas Henry Henry Wing en Bowdoin College , que también escribió para el MAA, aprobó más: " Proporciones divinasEs, sin duda, una valiosa adición a la literatura matemática. Desarrolla cuidadosamente un enfoque alternativo, inteligente y útil para la trigonometría y la geometría euclidiana que evitan la reflexión. No sería sorprendente si algunos de sus métodos finalmente se filtran en el desarrollo estándar de estos temas. Sin embargo, a menos que haya un cambio inesperado en los puntos de vista aceptados de los fundamentos de las matemáticas, no hay un caso sólido para que la trigonometría racional reemplace la teoría clásica " ^[3] Amanda Gefter, de New Scientist , describió el enfoque de Wildberger como un ejemplo. de finitismo . ^[2] James Franklinen el Matemático Inteligente argumentó que el libro merecía una consideración cuidadosa.^[4]

Un análisis realizado por Michael Gilsdorf de los problemas de ejemplo dados por Wildberger en un artículo anterior cuestionó la afirmación de que la RT requería menos pasos para resolver la mayoría de los problemas, si la selección libre de métodos clásicos (como la " fórmula del cordón " para el área de un triángulo desde Las coordenadas de sus vértices o la aplicación de un caso especial del teorema de Stewart directamente a un triángulo con una mediana se permiten para optimizar la solución de problemas. En cuanto a la pedagogía, y si el uso de las cantidades cuadráticas introducidas por RT ofrece beneficios reales sobre el aprendizaje tradicional, el autor observó que la trigonometría clásica no se basaba inicialmente en el uso de la serie de Taylor.para aproximarse a los ángulos en absoluto, sino más bien a las medidas de la cuerda (el doble del seno de un ángulo) y, por lo tanto, con una comprensión adecuada, los estudiantes podrían obtener ventajas continuas del uso de la medición lineal sin las inconsistencias lógicas reivindicadas cuando se introduce la parametrización circular por ángulo. ^[5]

Quadrance

La cuadratura y la distancia (como su raíz cuadrada) miden la separación de puntos en el espacio euclidiano. ^[6]Siguiendo el teorema de Pitágoras, la cuadratura de dos puntos A ₁ = ( x ₁ , y ₁ ) y A ₂ = ( x ₂ , y ₂ ) en un plano, por lo tanto, se define como la suma de los cuadrados de las diferencias en el plano.$${\ displaystyle x} y $${\ displaystyle y} coordenadas:

$${\ displaystyle Q (A_ {1}, A_ {2}) = (x_ {2} -x_ {1}) ^ {2} + (y_ {2} -y_ {1}) ^ {2}.}

La desigualdad del triángulo. $${\ displaystyle d_ {3} \ leq d_ {1} + d_ {2}} Se expresa bajo trigonometría racional como $${\ displaystyle (Q_ {3} -Q_ {1} -Q_ {2}) ^ {2} \ leq 4Q_ {1} Q_ {2}}.

Untado

Supongamos l ₁ y l ₂ se cortan en el punto A . Sea C el pie de la perpendicular de B a l ₂ . A continuación, la propagación es s = Q/R.

La extensión da una medida a la separación de dos líneas como un solo número sin dimensiones en el rango [0,1] (de paralelo a perpendicular ) para la geometría euclidiana. Reemplaza el concepto de (y tiene varias diferencias con respecto a) el ángulo discutido en la sección a continuación. Las descripciones de la propagación pueden incluir:

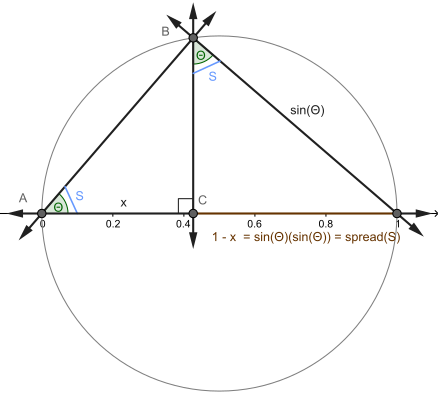
• Trigonometría (la más elemental): la relación sinusoidal de cuadriláteros en un triángulo rectángulo, equivalente al cuadrado del seno del ángulo ( izquierda ). ^[6] Al extender el lado adyacente AC para formar parte del diámetro de la unidad en un círculo y al considerar triángulos similares ( derecha ), la extensión se puede medir como la longitud (o la relación al diámetro) del segmento exterior, más tradicionalmente igual a la mitad veces (1 menos el coseno de dos veces el ángulo en A ) o haversina .

• Vector : como una función racional de las pendientes (y dirección relativa ) de un par de líneas donde se encuentran.

• Cartesiano : como una función racional de tres coordenadas utilizadas para atribuir dos vectores.

• El álgebra lineal (del producto punto ): una función racional normalizado: el cuadrado de la determinante de dos vectores (o par de líneas que se cortan) que forma una matriz dividida por el producto de sus quadrances.

Cálculo de la propagación

Trigonométrico

Suponga que dos líneas, l ₁ y l ₂ , se intersecan en el punto A como se muestra a la derecha. Elija un punto B ≠ A en l ₁ y sea C el pie de la perpendicular de B a l ₂ . Entonces la propagación s es ^[6]

$${\ displaystyle s (\ ell _ {1}, \ ell _ {2}) = {\ frac {Q (B, C)} {Q (A, B)}} = {\ frac {Q} {R} }.}

Vector / pendiente (dos variables)

Al igual que el ángulo, la dispersión depende solo de las pendientes relativas de dos líneas (los términos constantes se eliminan) y es invariante en la traducción (es decir, se conserva cuando las líneas se mueven manteniéndose paralelas a sí mismas). Así dadas dos líneas cuyas ecuaciones son

$${\ displaystyle a_ {1} x + b_ {1} y = {\ text {constant}} \ qquad {\ text {and}} \ qquad a_ {2} x + b_ {2} y = {\ text {constant }}}

Podemos reescribirlos como dos líneas que se encuentran en el origen (0, 0) con ecuaciones

$${\ displaystyle a_ {1} x + b_ {1} y = 0 \ qquad {\ text {y}} \ qquad a_ {2} x + b_ {2} y = 0}

En esta posición, el punto (- b ₁ , a ₁ ) satisface la primera ecuación y (- b ₂ , a ₂ ) satisface el segundo y los tres puntos (0, 0) , (- b ₁ , a ₁ ) y (- b ₂ , a ₂ ) formando la propagación daremos tres quadrances:

{\ displaystyle {\ begin {alineado} Q_ {1} & = \ left (b_ {1} ^ {2} + a_ {1} ^ {2} \ right), \\ Q_ {2} & = \ left ( b_ {2} ^ {2} + a_ {2} ^ {2} \ right), \\ Q_ {3} & = \ left (b_ {1} -b_ {2} \ right) ^ {2} + \ izquierda (a_ {1} -a_ {2} \ derecha) ^ {2} \ end {alineado}}}

El derecho cruzado - ver más abajo - en términos de propagación es

$${\ displaystyle 1-s = {\ frac {(Q_ {1} + Q_ {2} -Q_ {3}) ^ {2}} {4Q_ {1} Q_ {2}}}.}

que se convierte en:

$${\ displaystyle 1-s = {\ frac {\ left (a_ {1} ^ {2} + a_ {2} ^ {2} + b_ {1} ^ {2} + b_ {2} ^ {2} - (b_ {1} -b_ {2}) ^ {2} - (a_ {1} -a_ {2}) ^ {2} \ right) ^ {2}} {4 \ left (a_ {1} ^ { 2} + b_ {1} ^ {2} \ right) \ left (a_ {2} ^ {2} + b_ {2} ^ {2} \ right)}}.}

Esto simplifica, en el numerador, a (2 a ₁ a ₂ + 2 b ₁ b ₂ ) ² , dando:

$${\ displaystyle 1-s = {\ frac {\ left (a_ {1} a_ {2} + b_ {1} b_ {2} \ right) ^ {2}} {\ left (a_ {1} ^ {2 } + b_ {1} ^ {2} \ derecha) \ left (a_ {2} ^ {2} + b_ {2} ^ {2} \ right)}}.}

(Nota: 1 - s es la expresión para la cruz , el cuadrado del coseno de cualquiera de los ángulos entre un par de líneas o vectores, que le da su nombre a la ley de la cruz ).

Luego, usando la identidad Brahmagupta – Fibonacci

$${\ displaystyle \ left (a_ {2} b_ {1} -a_ {1} b_ {2} \ right) ^ {2} + \ left (a_ {1} a_ {2} + b_ {1} b_ {2 } \ right) ^ {2} = \ left (a_ {1} ^ {2} + b_ {1} ^ {2} \ right) \ left (a_ {2} ^ {2} + b_ {2} ^ { 2} \ derecha),}

La expresión estándar para la propagación en términos de pendientes (o direcciones) de dos líneas se convierte en

$${\ displaystyle s = {\ frac {\ left (a_ {1} b_ {2} -a_ {2} b_ {1} \ right) ^ {2}} {\ left (a_ {1} ^ {2} + b_ {1} ^ {2} \ right) \ left (a_ {2} ^ {2} + b_ {2} ^ {2} \ right)}}.}

En esta forma (y en su equivalente cartesiano que sigue) una propagación es la relación del cuadrado de un determinante de dos vectores (numerador) al producto de sus cuadrateces (denominador)

Cartesiano (tres variables)

Esto reemplaza (- b ₁ , a ₁ ) con ( x ₁ , y ₁ ) , (- b ₂ , a ₂ ) con ( x ₂ , y ₂ ) y el origen (0, 0) , como el punto de intersección de Dos líneas, con ( x ₃ , y ₃ ) en el resultado anterior:

$${\ displaystyle s = {\ frac {{\ bigl (} (y_ {1} -y_ {3}) (x_ {2} -x_ {3}) - (y_ {2} -y_ {3}) (x_ {1} -x_ {3}) {\ bigr)} ^ {2}} {{\ bigl (} (y_ {1} -y_ {3}) ^ {2} + (x_ {1} -x_ {3 }) ^ {2} {\ bigr)} {\ bigl (} (y_ {2} -y_ {3}) ^ {2} + (x_ {2} -x_ {3}) ^ {2} {\ bigr )}}}.}

Difusión en comparación con el ángulo

La extensión de dos líneas se puede medir en cuatro posiciones equivalentes.

A diferencia del ángulo, que puede definir una relación entre los rayos que emanan de un punto, mediante una parametrización de medición de arco , y donde un par de líneas pueden considerarse cuatro pares de rayos, formando cuatro ángulos, la "propagación" es más fundamental en la trigonometría racional, describiendo dos líneas por una sola medida de una función racional (ver arriba). ^[6] Al ser equivalente al cuadrado de un seno del ángulo correspondiente θ (y al eje del doble ángulo basado en la cuerda Δ = 2 θ ), la extensión de un ángulo y su ángulo suplementarioson iguales.

Untado	Ángulo ( θ )					Cantidad
pecado 2 ( θ )	Cuadrantes	Vueltas	Radianes	Grados	Gons	Unidad
0	0	0	0	0 °	0 g
1/4	1/3	1/12	π/6	30 °	33 1/3  g
1/2	1/2	1/8	π/4	45 °	50 g
3/4	2/3	1/6	π/3	60 °	66 2/3  g
1	1	1/4	π/2	90 °	100 g	lineas ortogonales
3/4	1 1/3	1/3	2 π/3	120 °	133 1/3  g
1/2	1 1/2	3/8	3 π/4	135 °	150 g
1/4	1 2/3	5/12	5 π/6	150 °	166 2/3  g
0	2	1/2	π	180 °	200 g

La propagación no es proporcional, sin embargo, a la separación entre líneas como lo sería el ángulo; con los diferenciales de 0, 1/4 , 1/2 , 3/4 , y 1 correspondientes a ángulos de manera desigual espaciados 0 °, 30 °, 45 °, 60 ° y 90 °.

En cambio, (recordando la propiedad complementaria) dos repartos co-terminales equivalentes determinan un tercer reparto, cuyo valor será una solución de la fórmula de reparto triple para un triángulo (o tres líneas concurrentes) que tienen repartos de s , s y r :

{\ displaystyle {\ begin {alineado} (2s + r) ^ {2} & = 2 \ left (2s ^ {2} + r ^ {2} \ right) + 4s ^ {2} r \\ 4s ^ { 2} + 4sr + r ^ {2} & = 4s ^ {2} + 2r ^ {2} + 4s ^ {2} r \ end {alineado}}}

dando el polinomio cuadrático (en s ):

{\ displaystyle {\ begin {alineado} r ^ {2} + 4s ^ {2} r-4sr & = 0 \\ r ^ {2} -4s (1-s) r & = 0 \ end {alineado}}}

y soluciones

$${\ displaystyle r = 0 \ quad ({\ text {trivial}}) \ qquad {\ text {o}} \ qquad r = 4s (1-s)}

Esto es equivalente a la identidad trigonométrica:

$${\ displaystyle \ sin ^ {2} (2 \ theta) = 4 \ sin ^ {2} \ theta \ left (1- \ sin ^ {2} \ theta \ right)}

de los ángulos θ , θ y 180 ° - 2 θ de un triángulo, usando

$${\ displaystyle S_ {2} (s) = S_ {2} \ left (\ sin ^ {2} \ theta \ right) = \ sin ^ {2} (2 \ theta) = r (s)}

Para denotar un segundo polinomio extendido en el s .

Encontrar el triple de una extensión del mismo modo hace uso de la fórmula de triple propagación como una ecuación cuadrática en la propagación tercero desconocido t tratamiento de los diferenciales conocidos s y r (la solución anterior) como constantes. Esto resulta (después de la eliminación de la 'pequeña' solución s ) a ser:

$${\ displaystyle S_ {3} (s) = s (3-4s) ^ {2} = t (s)}

Se pueden generar múltiplos adicionales de cualquier propagación básica de líneas si se continúa usando la fórmula de triple propagación de esta manera, o mediante el uso de una fórmula de recursión (ver más abajo) que se aplica de manera indirecta. Mientras que cualquier múltiplo de una propagación que sea racional será polinomial en esa propagación (y, por lo tanto, racional), lo contrario no se aplica. Por ejemplo, según la fórmula de medio ángulo , dos líneas que se juntan en un ángulo de 15 ° (o 165 °) tienen una extensión de:

$${\ displaystyle \ operatorname {hav} \ left (30 ^ {\ circ} \ right) = \ sin ^ {2} \ left ({\ frac {30 ^ {\ circ}} {2}} \ right) = { \ frac {1- \ cos 30 ^ {\ circ}} {2}} = {\ frac {1 - {\ frac {\ sqrt {3}} {2}}} {2}} = {\ frac {2 - {\ sqrt {3}}} {4}} \ approx 0.0667.}

y así existe por extensión algebraica de los números racionales.

Polinomios extendidos

Como se ve por los diferenciales de dobles y triples, un n º múltiple de cualquier extensión, s da un polinomio en esa difusión, denotado S _n ( s ) , como una solución a la fórmula de triple propagación.

En el lenguaje convencional de las funciones circulares , estos polinomios de grado n th , para n = 0, 1, 2, ... , se pueden caracterizar por la identidad: ^{[ citación necesaria ]}

$${\ displaystyle \ sin ^ {2} (n \ theta) = S_ {n} \ left (\ sin ^ {2} \ theta \ right).}

Identidades

Fórmulas explicitas

• $${\ displaystyle S_ {n} (s) = s \ sum _ {k = 0} ^ {n-1} {\ frac {n} {nk}} {\ binom {2n-1-k} {k}} (-4s) ^ {n-1-k}.}(Michael Hirschhorn, Shuxiang Goh) ^[1]
• $${\ displaystyle S_ {n} (s) = {\ tfrac {1} {2}} - {\ tfrac {1} {4}} \ left (1-2s + 2 {\ sqrt {s ^ {2} - s}} \ right) ^ {n} - {\ tfrac {1} {4}} \ left (1-2s-2 {\ sqrt {s ^ {2} -s}} \ right) ^ {n}. } (M. Hovdan)
• $${\ displaystyle S_ {n} (s) = - {\ tfrac {1} {4}} \ left (\ left ({\ sqrt {1-s}} + i {\ sqrt {s}} \ right) ^ {2n} -1 \ right) ^ {2} \ left ({\ sqrt {1-s}} - i {\ sqrt {s}} \ right) ^ {2n}.} (M. Hovdan)

De la definición se deduce inmediatamente que

$${\ displaystyle S_ {n} (s) = \ sin ^ {2} \ left (n \ arcsin \ left ({\ sqrt {s}} \ right) \ right).}^{[ cita requerida ]}

Formula de recursion

Desde la fórmula de triple propagación $${\ displaystyle (s_ {1} + s_ {2} + s_ {3}) ^ {2} = 2 \ left (s_ {1} ^ {2} + s_ {2} ^ {2} + s_ {3} ^ {2} \ derecha) + 4s_ {1} s_ {2} s_ {3}} Es una ecuación cuyas entradas pueden difundirse polinomios de la forma:$${\ displaystyle s}, $${\ displaystyle S_ {n} (s)} y $${\ displaystyle S_ {n + 1} (s)},

tomando la diferencia de las expresiones

$${\ displaystyle (s + S_ {n} (s) + S_ {n + 1} (s)) ^ {2} = 2 \ left (s ^ {2} + S_ {n} (s) ^ {2} + S_ {n + 1} (s) ^ {2} \ derecha) + 4sS_ {n} (s) S_ {n + 1} (s)} y

$${\ displaystyle (s + S_ {n} (s) + S_ {n-1} (s)) ^ {2} = 2 \ left (s ^ {2} + S_ {n} (s) ^ {2} + S_ {n-1} (s) ^ {2} \ right) + 4sS_ {n} (s) S_ {n-1} (s)}

y reorganizando, da una relación recursiva:

$${\ displaystyle S_ {n + 1} (s) = 2 (1-2s) S_ {n} (s) -S_ {n-1} (s) + 2s.}^[1]

Relación con los polinomios de Chebyshev

Los polinomios extendidos están relacionados con los polinomios de Chebyshev de primer tipo, T _n , por la identidad.

$${\ displaystyle 1-2S_ {n} (s) = T_ {n} (1-2s).}

Esto implica ^[1]

$${\ displaystyle S_ {n} (s) = {\ frac {1-T_ {n} (1-2s)} {2}} = 1-T_ {n} ^ {2} \ left ({\ sqrt {1 -s}} \ derecha).}

La segunda igualdad anterior se desprende de la identidad.

$${\ displaystyle 2T_ {n} ^ {2} (x) -1 = T_ {2n} (x)}

en los polinomios de Chebyshev. ^{[ cita requerida ]}

Composición

Los polinomios extendidos satisfacen la identidad de la composición ^[1]

$${\ displaystyle S_ {n} {\ bigl (} S_ {m} (s) {\ bigr)} = S_ {nm} (s).}

Coeficientes en campos finitos.

Cuando se toman los coeficientes a ser miembros de la finito campo F _p , entonces la secuencia { S _n } _{n = 0, 1, 2, ...} de los polinomios propagación es periódica con periodo p ² - 1/2 . En otras palabras, si k = p ² - 1/2 , entonces S _n + k = S _n , para todos  n . ^{[ cita requerida ]}

Ortogonalidad

Cuando los coeficientes se toman como reales , entonces para n ≠ m , tenemos ^[1]

$${\ displaystyle \ int _ {0} ^ {1} \ left (S_ {n} (s) - {\ tfrac {1} {2}} \ right) \ left (S_ {m} (s) - {\ tfrac {1} {2}} \ right) {\ frac {ds} {\ sqrt {s (1-s)}}} = 0.}

Para n = m , la integral es π/8 a menos que n = m = 0 , en cuyo caso es  π/4 . ^{[ cita requerida ]}

Funciones generadoras

La función generadora ordinaria es

$${\ displaystyle \ sum _ {n = 1} ^ {\ infty} S_ {n} (s) x ^ {n} = {\ frac {sx (1 + x)} {(1-x) ^ {3} + 4sx (1-x)}}.}(Michael Hirschhorn) ^[1]

La función generadora exponencial es

$${\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {S_ {n} (s)} {n!}} x ^ {n} = {\ tfrac {1} {2}} e ^ {x} \ left (1-e ^ {- 2sx} \ cos \ left (2x {\ sqrt {s (1-s)}} \ right) \ right).}^{[ cita requerida ]}

Ecuación diferencial

S _n ( s ) satisface la ecuación diferencial no homogénea lineal de segundo orden ^{[ cita requerida ]}

$${\ displaystyle s (1-s) y '' + \ left ({\ tfrac {1} {2}} - s \ right) y '+ n ^ {2} \ left (y - {\ tfrac {1} {2}} \ derecha) = 0.}

Teorema de periodicidad de la propagación

Para cada entero n y cada primo p , hay un número natural m tal que S _n ( s ) es divisible por p precisamente cuando m divide n . Este número m es un divisor de p - 1 o p + 1 . La prueba de este número de propiedad teórica fue dada por primera vez en un artículo por Shuxiang Goh y NJ Wildberger. ^[7] Implica considerar el análogo proyectivo a la quadrance en la línea proyectiva finita P¹ ( F _p ) .

Tabla de polinomios extendidos, con factorizaciones.

Los primeros polinomios extendidos son los siguientes:

${\displaystyle {\begin{aligned}S_{0}(s)={}&0\\[10pt]S_{1}(s)={}&s\\[10pt]S_{2}(s)={}&4s-4s^{2}\\={}&4s(1-s)\\[10pt]S_{3}(s)={}&9s-24s^{2}+16s^{3}\\={}&s(3-4s)^{2}\\[10pt]S_{4}(s)={}&16s-80s^{2}+128s^{3}-64s^{4}\\={}&16s(1-s)(1-2s)^{2}\\[10pt]S_{5}(s)={}&25s-200s^{2}+560s^{3}-640s^{4}+256s^{5}\\={}&s\left(5-20s+16s^{2}\right)^{2}\\[10pt]S_{6}(s)={}&36s-420s^{2}+1792s^{3}-3456s^{4}+3072s^{5}-1024s^{6}\\={}&4s(1-s)(1-4s)^{2}(3-4s)^{2}\\[10pt]S_{7}(s)={}&49s-784s^{2}+4704s^{3}-13440s^{4}+19712s^{5}-14336s^{6}+4096s^{7}\\={}&s\left(7-56s+112s^{2}-64s^{3}\right)^{2}\\[10pt]S_{8}(s)={}&64s-1344s^{2}+10752s^{3}-42240s^{4}+90112s^{5}-106496s^{6}\\&{}+65536s^{7}-16384s^{8}\\={}&64s(s-1)(1-2s)^{2}\left(1-8s+8s^{2}\right)^{2}\\[10pt]S_{9}(s)={}&81s-2160s^{2}+22176s^{3}-114048s^{4}+329472s^{5}-559104s^{6}\\&{}+552960s^{7}-294912s^{8}+65536s^{9}\\={}&s(-3+4s)^{2}\left(-3+36s-96s^{2}+64s^{3}\right)^{2}\\[10pt]S_{10}(s)={}&100s-3300s^{2}+42240s^{3}-274560s^{4}+1025024s^{5}\\&{}-2329600s^{6}+3276800s^{7}-2785280s^{8}+1310720s^{9}-262144s^{10}\\={}&4s(1-s)\left(5-20s+16s^{2}\right)^{2}\left(1-12s+16s^{2}\right)^{2}\\[10pt]S_{11}(s)={}&121s-4840s^{2}+75504s^{3}-604032s^{4}+2818816s^{5}\\&{}-8200192s^{6}+15319040s^{7}-18382848s^{8}+13697024s^{9}-5767168s^{10}+1048576s^{11}\\={}&s\left(11-220s+1232s^{2}-2816s^{3}+2816s^{4}-1024s^{5}\right)^{2}\end{aligned}}}$

Leyes de la trigonometría racional.

Wildberger afirma que hay cinco leyes básicas en la trigonometría racional. También afirma que estas leyes se pueden verificar utilizando las matemáticas de nivel secundario. Algunos son equivalentes a las fórmulas trigonométricas estándar con las variables expresadas en cuadratura y propagación. ^[6]

En las siguientes cinco fórmulas, tenemos un triángulo formado por tres puntos A ₁ , A ₂ , A ₃ . Las distribuciones de los ángulos en esos puntos son s ₁ , s ₂ , s ₃ y Q ₁ , Q ₂ , Q ₃ , son los cuadriláteros de los lados del triángulo opuestos a A ₁ , A ₂ , A ₃ , respectivamente. Como en la trigonometría clásica, si conocemos tres de los seis elementos s ₁ , s ₂, s ₃ , Q ₁ , Q ₂ , Q ₃ , y estos tres no son los tres s , entonces podemos calcular los otros tres.

Fórmula triple cuádruple

Los tres puntos A ₁ , A ₂ , A ₃ son colineales si y solo si:

$${\ displaystyle (Q_ {1} + Q_ {2} + Q_ {3}) ^ {2} = 2 \ left (Q_ {1} ^ {2} + Q_ {2} ^ {2} + Q_ {3} ^ {2} \ derecha)}

donde Q ₁ , Q ₂ , Q ₃ representan los cuadriláteros entre A ₁ , A ₂ , A ₃ respectivamente. Puede probarse por geometría analítica (el medio preferido dentro de la trigonometría racional) o derivado de la fórmula de Heron , usando la condición de colinealidad de que el triángulo formado por los tres puntos tiene área cero.

espectáculo

Prueba (haga clic a la derecha para mostrar / ocultar)

Teorema de Pitágoras

Las líneas A ₁ A ₃ (de quadrance Q ₁ ) y A ₂ A ₃ (de quadrance Q ₂ ) son perpendiculares (su extensión es 1) si y solo si:

$${\ displaystyle Q_ {1} + Q_ {2} = Q_ {3}.}

donde Q ₃ es la quadrance entre A ₁ y A ₂ .

Esto es equivalente al teorema de Pitágoras (y su inverso).

Hay muchas pruebas clásicas del teorema de Pitágoras ; Este está enmarcado en los términos de la trigonometría racional.

La extensión de un ángulo es el cuadrado de su seno . Dado el triángulo △ ABC con una extensión de 1 entre los lados AB y AC ,

$${\ displaystyle Q (AB) + Q (AC) = Q (BC)}

donde Q es la "quadrance", es decir, el cuadrado de la distancia.

espectáculo

Prueba

Difundir la ley

Para cualquier triángulo △ A ₁ A ₂ A ₃ con cuadrículas distintas de cero: ^[1]

$${\ displaystyle {\ frac {s_ {1}} {Q_ {1}}} = {\ frac {s_ {2}} {Q_ {2}}} = {\ frac {s_ {3}} {Q_ {3 }}}.}

Esta es la ley de los senos , justo al cuadrado.

Ley de cruce

Para cualquier triángulo △ A ₁ A ₂ A ₃ , ^[1]

$${\ displaystyle (Q_ {1} + Q_ {2} -Q_ {3}) ^ {2} = 4Q_ {1} Q_ {2} (1-s_ {3}).}

Esto es análogo a la ley de los cosenos . Se llama la 'ley de la cruz' porque (1 - s ₃ ) , el cuadrado del coseno del ángulo, se llama la 'cruz'.

Fórmula de triple propagación

Para cualquier triángulo △ A ₁ A ₂ A ₃ , ^[1]

$${\ displaystyle (s_ {1} + s_ {2} + s_ {3}) ^ {2} = 2 \ left (s_ {1} ^ {2} + s_ {2} ^ {2} + s_ {3} ^ {2} \ derecha) + 4s_ {1} s_ {2} s_ {3}.}

Esta relación se puede derivar de la fórmula para el seno de un ángulo compuesto : en un triángulo (cuyos tres ángulos suman 180 °) tenemos,

$${\ displaystyle \ sin (a) = \ sin (b + c) = \ sin (b) \ cos (c) + \ sin (c) \ cos (b)}.

De manera equivalente, describe la relación entre las extensiones de tres líneas concurrentes, ya que la dispersión (como el ángulo) no se ve afectada cuando los lados de un triángulo se mueven paralelos entre sí para reunirse en un punto común.

Saber dos diferenciales permite calcular la tercera resolviendo la fórmula cuadrática asociada pero, dado que son posibles dos soluciones, se deben usar otras reglas de propagación de triángulos para seleccionar la adecuada. (La compatibilidad de este método contrasta con la obtención de un ángulo suplementario directamente restando).

Trigonometría sobre campos arbitrarios.

Como las leyes de la trigonometría racional dan relaciones algebraicas (y no trascendentales), se aplican en general a los campos numéricos algebraicos más allá de los números racionales. Específicamente, cualquier campo finito que no tenga la característica 2 reproduce una forma de estas leyes, y por lo tanto una geometría de campo finito . ^[8] El 'plano' formado por un campo finito F _p es el producto cartesiano F _p × F _p de todos los pares ordenados de elementos de campo, con bordes opuestos identificados que forman la superficie topológicamente equivalente a un toro discretizado . Los elementos individuales corresponden a 'puntos' y 'líneas' estándar a conjuntos de no más de$${\ displaystyle p} puntos relacionados por incidencia (un punto inicial) más la dirección o la pendiente dada en los términos más bajos (diga todos los puntos "2 sobre y 1 arriba") que "envuelven" el plano antes de repetir.

Ejemplo: (verifique la ley de propagación en F ₁₃ )

La figura (derecha) muestra un triángulo de tres de estas líneas en la configuración de campo finito F ₁₃ × F ₁₃ :

Cada línea tiene su propio símbolo y las intersecciones de las líneas ( vértices ) están marcadas por dossímbolos presentes en los puntos:

Un triángulo a través de los puntos (2, 8) , (9, 9) y (10, 0) del campo finito - plano F ₁₃ × F ₁₃ .

(2, 8), (9, 9) y (10, 0).

Usando el teorema de Pitágoras con el módulo aritmético 13, encontramos que estos lados tienen quadrances de:

(9 - 2) ² + (9 - 8) ² = 50 ≡ 11 mod 13

(9 - 10) ² + (9 - 0) ² = 82 ≡ 4 mod 13

(10 - 2) ² + (0 - 8) ² = 128 ≡ 11 mod 13

Reorganizando la ley de la cruz como

$${\ displaystyle s_ {3} = 1 - {\ frac {(Q_ {1} + Q_ {2} -Q_ {3}) ^ {2}} {4Q_ {1} Q_ {2}}}}

da expresiones separadas para cada propagación, en términos de los tres cuadriláteros:

1 - ( 4 + 11 - 11 ) ²/4 × 4 × 11 = 13/7 ≡ 8 mod 13

1 - ( 11 + 11 - 4 ) ²/4 x 11 x 11 = 1 - 12/3 ≡ 10 mod 13

1 - ( 4 + 11 - 11 ) ²/4 × 4 × 11 = 13/7 ≡ 8 mod 13

A su vez, observamos que todos estos índices son iguales, según la ley de propagación (al menos en la modificación 13):

8/11  :10/4  :8/11

Como la primera y la última relación coinciden (haciendo que el triángulo sea isósceles ) simplemente cruzamos la multiplicación, y tomamos las diferencias, para mostrar igualdad con la proporción media también:

11 × 10 - 8 × 4 = 78 ≡ 0 mod 13

De lo contrario, se considera que el plano euclidiano estándar consiste solo en puntos racionales, ℚ × ℚ , omitiendo cualquier número no algebraico como soluciones. Propiedades como la incidencia de objetos, que representan las soluciones o el "contenido" de los teoremas geométricos, por lo tanto, siguen un enfoque teórico numérico que difiere y es más restrictivo que uno que permite números reales. Por ejemplo, no se considera que todas las líneas que pasan por el centro de un círculo se encuentran con el círculo en su circunferencia. Para ser incidente dichas líneas deben ser de la forma.

{\ displaystyle {\ begin {alineado} ax + by & = 0 \\ a ^ {2} + b ^ {2} & = c ^ {2} \ end {alineado}} \ quad a, b, c \ in \ mathbb {Q}}

y necesariamente se encuentran con el círculo en un punto racional .

Computación - complejidad y eficiencia

La trigonometría racional hace que casi todos los problemas se solucionen solo con la suma, la resta, la multiplicación o la división, ya que las funciones trigonométricas (del ángulo) se evitan a propósito a favor de las relaciones trigonométricas en forma cuadrática. ^[6] A lo sumo, por lo tanto, los resultados requeridos como distancia (o ángulo) pueden aproximarse a partir de un equivalente racional de valor exacto de quadrance (o dispersión) después de que se hayan realizado estas operaciones más simples. Sin embargo, para hacer uso de esta ventaja, cada problema debe darse, o configurarse, en términos de quadrances y spreads anteriores, lo que implica un trabajo adicional. ^[9]

Las leyes de la trigonometría racional, que son algebraicas y de "valor exacto", introducen sutilezas en las soluciones de los problemas, como la falta de aditivación de cuadriláteros de puntos colineales (en el caso de la fórmula del triple cuádruple) o la propagación de líneas concurrentes. (en el caso de la fórmula de triple propagación) ausente del sujeto clásico, donde la linealidad se incorpora a la distancia y la medida circular de los ángulos, aunque sean técnicas "trascendentales", que requieren una aproximación en los resultados.