TRIGONOMETRÍA

diagrama de Greninger ^[1] / ɡ r ɛ n ɪ ŋ ər / es un gráfico que permite las relaciones angulares entre las zonas y planos en un cristal para ser leídos directamente de una difracción de rayos xfotografía.

El gráfico de Greninger es una herramienta trigonométrica simple para determinar g y d para una distancia fija de muestra a película. (Si uno usa un detector 2-d, el problema de determinar g y d podría resolverse matemáticamente usando las ecuaciones que generan el gráfico de Greninger) Se debe generar un nuevo gráfico para diferentes distancias a las distancias del detector. (2 s es 2 q para el pico de difracción y tan  m es x / y para las coordenadas cartesianas del pico de difracción.) El gráfico de Greninger da directamente los dos ángulos necesarios para trazar los polos en la red Wulff. Es crítico hacer un seguimiento de la disposición relativa de la muestra a la película, si se usa película fotográfica, esto se logra cortando la esquina de la película. Para la película Polaroid , se debe tomar nota de la disposición de la cara de la película en la cámara.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Gráfica de la función gudermanniana.

La función Gudermannian , llamada así por Christoph Gudermann (1798–1852), relaciona las funciones circularesy las funciones hiperbólicas sin usar explícitamente números complejos .

Se define para todas las x por ^{[1] [2] [3]}

$${\ displaystyle \ operatorname {gd} x = \ int _ {0} ^ {x} {\ frac {1} {\ cosh t}} \, dt.}

Propiedades [ editar ]

Definiciones alternativas [ editar ]

{\ displaystyle {\ begin {alineado} \ operatorname {gd} x & = \ arcsin \ left (\ tanh x \ right) = \ arctan (\ sinh x) = \ operatorname {arccsc} (\ coth x) \\ & = \ operatorname {sgn} (x) \ cdot \ arccos \ left (\ operatorname {sech} x \ right) = \ operatorname {sgn} (x) \ cdot \ operatorname {arcsec} (\ cosh x) \\ & = 2 \ arctan \ left [\ tanh \ left ({\ tfrac {1} {2}} x \ right) \ right] \\ & = 2 \ arctan (e ^ {x}) - {\ tfrac {1} {2 }} \ pi. \ end {alineado}}}

Algunas identidades [ editar ]

{\ displaystyle {\ begin {alineado} \ sin (\ operatorname {gd} x) = \ tanh x; \ quad & \ csc (\ operatorname {gd} x) = \ coth x; \\\ cos (\ operatorname { gd} x) = \ operatorname {sech} x; \ quad & \ sec (\ operatorname {gd} x) = \ cosh x; \\\ tan (\ operatorname {gd} x) = \ sinh x; \ quad & \ cot (\ operatorname {gd} x) = \ operatorname {csch} x; \\\ tan ({\ tfrac {1} {2}} \ operatorname {gd} x) = \ tanh ({\ tfrac {1} {2}} x). \ End {alineado}}}

Inverso [ editar ]

Gráfica de la función gudermanniana inversa.

${\displaystyle {\begin{aligned}\operatorname {gd} ^{-1}x&=\int _{0}^{x}{\frac {1}{\cos t}}\,dt\qquad -\pi /2$

(Ver funciones hiperbólicas inversas .)

Algunas identidades [ editar ]

{\ displaystyle {\ begin {alineado} \ sinh (\ operatorname {gd} ^ {- 1} x) = \ tan x; \ quad & \ operatorname {csch} (\ operatorname {gd} ^ {- 1} x) = \ cot x; \\\ cosh (\ operatorname {gd} ^ {- 1} x) = \ sec x; \ quad & \ operatorname {sech} (\ operatorname {gd} ^ {- 1} x) = \ cos x; \\\ tanh (\ operatorname {gd} ^ {- 1} x) = \ sin x; \ quad & \ coth (\ operatorname {gd} ^ {- 1} x) = \ csc x. \ end {alineado}}}

Derivados [ editar ]

$${\ displaystyle {\ frac {d} {dx}} \ operatorname {gd} x = \ operatorname {sech} x; \ quad {\ frac {d} {dx}} \; \ operatorname {gd} ^ {- 1 } x = \ sec x.}

Historia [ editar ]

Johann Heinrich Lambert introdujo la función en la década de 1760 al mismo tiempo que las funciones hiperbólicas . Él lo llamó el "ángulo trascendente", y tuvo varios nombres hasta 1862 cuando Arthur Cayleysugirió que se le diera su nombre actual como un tributo al trabajo de Gudermann en la década de 1830 sobre la teoría de las funciones especiales. ^[4] Gudermann había publicado artículos en Crelle's Journal que se recopilaron en Theorie der potenzial- oder cyklisch-hyperbolischen Functionen (1833), un libro que expone el sinhy el cosh a una amplia audiencia (bajo la apariencia de$${\ displaystyle {\ mathfrak {Sin}}} y $${\ displaystyle {\ mathfrak {Cos}}}).

La notación gd fue introducida por Cayley ^[5], donde comienza llamando a gd. u el inverso de la integral de la función secante :

$${\ displaystyle u = \ int _ {0} ^ {\ phi} \ sec t \, dt = \ ln \ left (\ tan \ left ({\ tfrac {1} {4}} \ pi + {\ tfrac { 1} {2}} \ phi \ right) \ right)}

y luego deriva "la definición" de lo trascendente:

$${\ displaystyle \ operatorname {gd} u = i ^ {- 1} \ ln \ left (\ tan \ left ({\ tfrac {1} {4}} \ pi + {\ tfrac {1} {2}} ui \bien bien)}

observando inmediatamente que es una función real de u .

Aplicaciones [ editar ]

• El ángulo de la función de paralelismo en la geometría hiperbólica se define por

$${\ displaystyle {\ tfrac {1} {2}} \ pi - \ operatorname {gd} x}

• En una proyección de Mercator, una línea de latitud constante es paralela al ecuador (en la proyección) y se desplaza en una cantidad proporcional al Gudermannian inverso de la latitud.
• El Gudermannian (con un argumento complejo) se puede usar en la definición de la proyección de Mercator transversal . ^[6]

• El Gudermannian aparece en una solución no periódica del péndulo invertido . ^[7]

• El Gudermannian también aparece en una solución de espejo móvil del efecto Casimir dinámico .

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

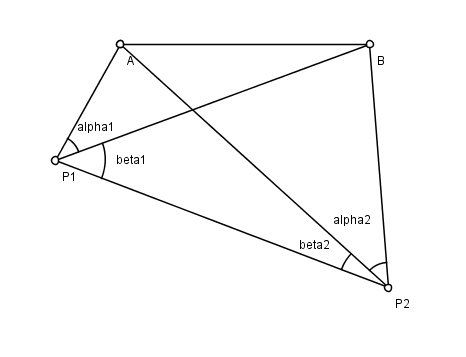
El problema de Hansen es un problema en el estudio planar , que lleva el nombre del astrónomo Peter Andreas Hansen (1795–1874), que trabajó en el estudio geodésico de Dinamarca. Hay dos puntos conocidos A y B , y dos puntos desconocidos P ₁ y P ₂ . Desde P ₁ y P _2, un observador mide los ángulos formados por las líneas de visión a cada uno de los otros tres puntos. El problema es encontrar las posiciones de P ₁ y P ₂ . Ver figura; Los ángulos medidos son ( α ₁ ,  β₁ ,  α ₂ ,  β ₂ ).

Como se trata de observaciones de ángulos realizados en puntos desconocidos, el problema es un ejemplo de resección (en oposición a una intersección).

Visión general del método de solución [ editar ]

Defina los siguientes ángulos: γ  =  P ₁ AP ₂ , δ  =  P ₁ BP ₂ , φ  =  P ₂ AB , ψ  =  P ₁ BA . Como primer paso resolveremos para φ y ψ . La suma de estos dos ángulos desconocidos es igual a la suma de β ₁ y β ₂ , produciendo la ecuación

$${\ displaystyle \ phi + \ psi = \ beta _ {1} + \ beta _ {2}.}

Una segunda ecuación se puede encontrar más laboriosamente, como sigue. La ley de los senos cede.

$${\ displaystyle {\ frac {AB} {P_ {2} B}} = {\ frac {\ sin \ alpha _ {2}} {\ sin \ phi}}} y

$${\ displaystyle {\ frac {P_ {2} B} {P_ {1} P_ {2}}} = {\ frac {\ sin \ beta _ {1}} {\ sin \ delta}}.}

Combinando estos, obtenemos

$${\ displaystyle {\ frac {AB} {P_ {1} P_ {2}}} = {\ frac {\ sin \ alpha _ {2} \ sin \ beta _ {1}} {\ sin \ phi \ sin \ delta}}.}

Razonamiento totalmente análogo en los rendimientos del otro lado.

$${\ displaystyle {\ frac {AB} {P_ {1} P_ {2}}} = {\ frac {\ sin \ alpha _ {1} \ sin \ beta _ {2}} {\ sin \ psi \ sin \ gamma}}.}

Ajustando estos dos iguales da

$${\ displaystyle {\ frac {\ sin \ phi} {\ sin \ psi}} = {\ frac {\ sin \ gamma \ sin \ alpha _ {2} \ sin \ beta _ {1}} {\ sin \ delta \ sin \ alpha _ {1} \ sin \ beta _ {2}}} = k.}

Usando una identidad trigonométrica conocida , esta relación de senos se puede expresar como la tangente de una diferencia de ángulo:

$${\ displaystyle \ tan {\ frac {\ phi - \ psi} {2}} = {\ frac {k-1} {k + 1}} \ tan {\ frac {\ phi + \ psi} {2}} .}

Esta es la segunda ecuación que necesitamos. Una vez que resolvemos las dos ecuaciones para las dos incógnitas.$${\ displaystyle \ phi} y $${\ displaystyle \ psi}, podemos usar cualquiera de las dos expresiones anteriores para $${\ displaystyle {\ frac {AB} {P_ {1} P_ {2}}}}para encontrar P ₁ P ₂ya que AB es conocido. Entonces podemos encontrar todos los otros segmentos usando la ley de los senos. ^[1]

Algoritmo de solución [ editar ]

Nos dan cuatro ángulos ( α ₁ ,  β ₁ ,  α ₂ ,  β ₂ ) y la distancia AB . El cálculo procede de la siguiente manera:

• Calcular $${\ displaystyle \ gamma = \ pi - \ alpha _ {1} - \ beta _ {1} - \ beta _ {2}, \ quad \ delta = \ pi - \ alpha _ {2} - \ beta _ {1 } - \ beta _ {2}.}
• Calcular $${\ displaystyle k = {\ frac {\ sin \ gamma \ sin \ alpha _ {2} \ sin \ beta _ {1}} {\ sin \ delta \ sin \ alpha _ {1} \ sin \ beta _ {2 }}}.}
• Dejar $${\ displaystyle s = \ beta _ {1} + \ beta _ {2}, \ quad d = 2 \ arctan \ left [{\ frac {k-1} {k + 1}} \ tan (s / 2) \Correcto]} y entonces $${\ displaystyle \ phi = (s + d) / 2, \ quad \ psi = (sd) / 2.}
• Calcular

$${\ displaystyle P_ {1} P_ {2} = AB {\ frac {\ sin \ phi \ sin \ delta} {\ sin \ alpha _ {2} \ sin \ beta _ {1}}}}

o equivalente

$${\ displaystyle P_ {1} P_ {2} = AB {\ frac {\ sin \ psi \ sin \ gamma} {\ sin \ alpha _ {1} \ sin \ beta _ {2}}}.}

Si una de estas fracciones tiene un denominador cercano a cero, use la otra.