TRIGONOMETRÍA

 la identidad cotangente de Hermite es una identidad trigonométrica descubierta por Charles Hermite . ^[1] Supongamos que a ₁ , ...,  a _n son números complejos , ninguno de los cuales difiere por un múltiplo entero de  π . Dejar

$${\ displaystyle A_ {n, k} = \ prod _ {\ begin {smallmatrix} 1 \ leq j \ leq n \\ j \ neq k \ end {smallmatrix}} \ cot (a_ {k} -a_ {j} )}

(En particular, A _1,1 , al ser un producto vacío , es 1). Entonces

$${\ displaystyle \ cot (z-a_ {1}) \ cdots \ cot (z-a_ {n}) = \ cos {\ frac {n \ pi} {2}} + \ sum _ {k = 1} ^ {n} A_ {n, k} \ cot (z-a_ {k}).}

El ejemplo más simple no trivial es el caso  n  = 2:

$${\ displaystyle \ cot (z-a_ {1}) \ cot (z-a_ {2}) = - 1+ \ cot (a_ {1} -a_ {2}) \ cot (z-a_ {1}) + \ cot (a_ {2} -a_ {1}) \ cot (z-a_ {2}). \,}

hipotenusa es el lado más largo de un triángulo rectángulo , el lado opuesto al ángulo recto . La longitud de la hipotenusa de un triángulo rectángulo se puede encontrar usando el teorema de Pitágoras , que establece que el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados. Por ejemplo, si uno de los otros lados tiene una longitud de 3 (cuando está al cuadrado, 9) y el otro tiene una longitud de 4 (cuando está al cuadrado, 16), entonces sus cuadrados suman 25. La longitud de la hipotenusa es la raíz cuadrada de 25, es decir, 5.

Etimología [ editar ]

Mire para arribaὑποτείνουσα en Wiktionary, el diccionario gratuito.

La palabra hipotenusa se deriva de griego eta τὴν ὀρθὴν γωνίαν ὑποτείνουσα (sc. Γραμμή o πλευρά ), que significa "[lado] que subtiendeel ángulo derecho" ( Apolodoro ), ^[1] ὑποτείνουσα hupoteinousa siendo el participio activo presente femenino del verbo ὑποτείνω hupo -teinō"estirar abajo, subtender", desde τείνω teinō "estirar, extender". El participio nominalizado, ἡ ὑποτείνουσα , se usó para la hipotenusa de un triángulo en el siglo IV a. C. (atestiguado en Platón , Timeo).54d). El término griego se prestó al latín tardío , como hipotunnsa . La adopción como un latinismo aprendido utilizado en las lenguas modernas data del siglo XVI. ^[2] La ortografía en -e , como hipotenusa , es de origen francés ( Estienne de La Roche 1520). ^[3]

El cálculo de la hipotenusa [ editar ]

Un triángulo rectángulo y su hipotenusa, h , junto con catetos(piernas) c ₁ y c ₂ .

La longitud de la hipotenusa se calcula utilizando la función de raíz cuadrada implícita en el teorema de Pitágoras . Usando la notación común de que la longitud de las dos patas del triángulo (los lados perpendiculares entre sí) son a y b, y la de la hipotenusa es c , tenemos

$${\ displaystyle c = {\ sqrt {a ^ {2} + b ^ {2}}}.}

El teorema de Pitágoras, y por lo tanto esta longitud, también puede derivarse de la ley de los cosenos al observar que el ángulo opuesto a la hipotenusa es de 90 ° y observar que su coseno es 0:

$${\ displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2ab \ cos 90 ^ {\ circ} = a ^ {2} + b ^ {2} \ por lo tanto c = {\ sqrt { a ^ {2} + b ^ {2}}}.}

Muchos lenguajes informáticos son compatibles con la función estándar ISO C hipot ( x , y ), que devuelve el valor anterior. La función está diseñada para no fallar donde el cálculo directo puede desbordarse o subdesbordarse y puede ser un poco más preciso.

Algunas calculadoras científicas proporcionan una función para convertir de coordenadas rectangulares a coordenadas polares . Esto da tanto la longitud de la hipotenusa como el ángulo que forma la hipotenusa con la línea de base ( c ₁ arriba) al mismo tiempo cuando se dan x e y . El ángulo devuelto normalmente viene dado por atan2 ( y , x ).

Propiedades [ editar ]

En la figura, a es la hipotenusa y b y c son el catéter. La proyección ortográfica de b es m , y de c es n .

Proyecciones ortográficas :

• La longitud de la hipotenusa es igual a la suma de las longitudes de las proyecciones ortográficas de ambos catetos. Y
• El cuadrado de la longitud de un cateto es igual al producto de las longitudes de su proyección ortográfica en la hipotenusa multiplicada por la longitud de esta.

b² = a · m

c² = a · n

• Además, la longitud de un cateto b es la media proporcional entre las longitudes de su proyección m y la hipotenusa a .

a / b = b / m

a / c = c / n

Relaciones trigonométricas [ editar ]

Por medio de relaciones trigonométricas , se puede obtener el valor de dos ángulos agudos,$${\ displaystyle \ alpha \,} y $${\ displaystyle \ beta \,}, del triángulo rectángulo.

Dada la longitud de la hipotenusa. $${\ displaystyle c \,} y de un cateto $${\ displaystyle b \,}, la relación es:

$${\ displaystyle {\ frac {b} {c}} = \ sin (\ beta) \,}

La función inversa trigonométrica es:

$${\ displaystyle \ beta \ = \ arcsin \ left ({\ frac {b} {c}} \ right) \,}

en el cual $${\ displaystyle \ beta \,} es el ángulo opuesto al cateto $${\ displaystyle b \,}.

El ángulo adyacente del catéter. $${\ displaystyle b \,} es $${\ displaystyle \ alpha \,} = 90 ° - $${\ displaystyle \ beta \,}

También se puede obtener el valor del ángulo. $${\ displaystyle \ beta \,} por la ecuación:

$${\ displaystyle \ beta \ = \ arccos \ left ({\ frac {a} {c}} \ right) \,}

en el cual $${\ displaystyle a \,} es el otro cateto.

Este artículo es sobre la ley de los cosenos en la geometría euclidiana . Para la ley del coseno de la óptica, vea la ley del coseno de Lambert .

Figura 1 - Un triángulo. Los ángulos α (o A ), β (o B ) y γ (o C ) son respectivamente opuestos a los lados a , b y c .

Trigonometría
contorno Historia Uso Funciones  ( inverso ) Trigonometría generalizada
Referencia
Identidades Constantes exactas Mesas Circulo unitario
Leyes y teoremas
Sines Cosenos Tangentes Cotangentes Teorema de pitágoras
Cálculo
Sustitución trigonométrica Integrales  ( funciones inversas ) Derivados
v t mi

En trigonometría , la ley de los cosenos (también conocida como la fórmula del coseno o la regla del coseno ) relaciona las longitudes de los lados de un triángulo con el coseno de uno de sus ángulos . Usando la notación como en la Fig. 1, la ley de los cosenos establece

$${\ displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2ab \ cos \ gamma,}

donde γ denota el ángulo contenido entre los lados de las longitudes a y b y opuesto al lado de la longitud c .

La ley de los cosenos generaliza el teorema de Pitágoras , que se aplica solo a los triángulos rectos : si el ángulo γ es un ángulo recto (de medida 90 grados , o π/2 radianes ), entonces cos γ = 0 , y así la ley de los cosenos se reduce al teorema de Pitágoras :

$${\ displaystyle c ^ {2} = a ^ {2} + b ^ {2}.}

La ley de los cosenos es útil para calcular el tercer lado de un triángulo cuando se conocen dos lados y su ángulo cerrado, y para calcular los ángulos de un triángulo si se conocen los tres lados.

Historia [ editar ]

Fig. 2 - Triángulo obtuso ABCcon BH perpendicular

Aunque la noción del coseno aún no se había desarrollado en su época, los Elementos de Euclides , que se remontan al siglo III aC, contienen un teorema geométrico temprano casi equivalente a la ley de los cosenos. Los casos de triángulos obtusos y triángulos agudos (correspondientes a los dos casos de coseno negativo o positivo) se tratan por separado, en las Propuestas 12 y 13 del Libro 2. Las funciones trigonométricas y el álgebra (en particular, los números negativos) están ausentes en el tiempo de Euclides. La declaración tiene un sabor más geométrico:

Proposición 12 
En los triángulos de ángulo obtuso, el cuadrado del lado que subtiende el ángulo obtuso es mayor que los cuadrados de los lados que contienen el ángulo obtuso por dos veces el rectángulo contenido por uno de los lados sobre el ángulo obtuso, es decir, aquel sobre el que cae la perpendicular , y la línea recta cortada en el exterior por la perpendicular hacia el ángulo obtuso.

-  Elementos de Euclides , traducción de Thomas L. Heath . ^[1]

Usando la notación como en la Fig. 2, la declaración de Euclides puede representarse por la fórmula

$${\ displaystyle AB ^ {2} = CA ^ {2} + CB ^ {2} +2 (CA) (CH).}

Esta fórmula puede transformarse en la ley de los cosenos al observar que CH = ( CB ) cos (π - γ ) = - ( CB ) cos γ . La Proposición 13 contiene una declaración completamente análoga para los triángulos agudos.

Los Elementos de Euclides allanaron el camino para el descubrimiento de la ley de los cosenos. En el siglo XV, Jamshīd al-Kāshī , un matemático y astrónomo persa, proporcionó la primera declaración explícita de la ley de los cosenos en una forma adecuada para la triangulación . Proporcionó tablas trigonométricas precisas y expresó el teorema en una forma adecuada para el uso moderno. En Francia , la ley de los cosenos todavía se conoce como Théorème d'Al-Kashi. ^{[2] [3] [4]}

El teorema fue popularizado en el mundo occidental por François Viète en el siglo XVI. A principios del siglo XIX, la notación algebraica moderna permitía que la ley de los cosenos se escribiera en su forma simbólica actual.

Aplicaciones [ editar ]

Fig. 3 - Aplicaciones de la ley de los cosenos: lado desconocido y ángulo desconocido.

El teorema se usa en la triangulación , para resolver un triángulo o círculo, es decir, para encontrar (ver Figura 3):

• el tercer lado de un triángulo si uno conoce dos lados y el ángulo entre ellos:

$${\ displaystyle \, c = {\ sqrt {a ^ {2} + b ^ {2} -2ab \ cos \ gamma}} \ ,;}

• los ángulos de un triángulo si uno conoce los tres lados:

$${\ displaystyle \, \ gamma = \ arccos \ left ({\ frac {a ^ {2} + b ^ {2} -c ^ {2}} {2ab}} \ right) \ ,;}

• el tercer lado de un triángulo si uno conoce dos lados y un ángulo opuesto a uno de ellos (uno también puede usar el teorema de Pitágoras para hacer esto si es un triángulo rectángulo ):

$${\ displaystyle \, a = b \ cos \ gamma \ pm {\ sqrt {c ^ {2} -b ^ {2} \ sin ^ {2} \ gamma}} \ ,.}

Estas fórmulas producen altos errores de redondeo en los cálculos de punto flotante si el triángulo es muy agudo, es decir, si c es pequeño en relación con a y b o γ es pequeño en comparación con 1. Incluso es posible obtener un resultado ligeramente mayor que uno Para el coseno de un ángulo.

La tercera fórmula que se muestra es el resultado de resolver para a en la ecuación cuadrática a ² - 2 ab cos γ + b ² - c ² = 0 . Esta ecuación puede tener 2, 1 o 0 soluciones positivas correspondientes al número de triángulos posibles dados los datos. Tendrá dos soluciones positivas si b sin γ < c < b , solo una solución positiva si c = b sin γ , y ninguna solución si c < b sin γ oc ≥ b . Estos diferentes casos también se explican por la ambigüedad de congruencia del ángulo lateral .

Pruebas [ editar ]

Usando la fórmula de la distancia [ editar ]

Fig. 4 - Prueba de geometría de coordenadas

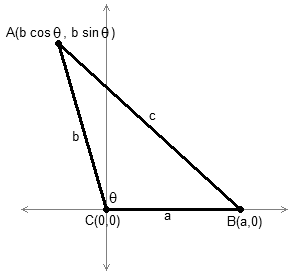
Considere un triángulo con lados de longitud a , b , c , donde θ es la medida del ángulo opuesto al lado de longitud c . Este triángulo se puede colocar en el sistema de coordenadas cartesiano trazando los siguientes puntos, como se muestra en la Fig. 4:

$${\ displaystyle A = (b \ cos \ theta, b \ sin \ theta), B = (a, 0), {\ text {y}} C = (0,0).}

Por la fórmula de distancia , tenemos

$${\ displaystyle c = {\ sqrt {(ab \ cos \ theta) ^ {2} + (0-b \ sin \ theta) ^ {2}}}.}

Ahora, solo trabajamos con esa ecuación:

{\ displaystyle {\ begin {alineado} c ^ {2} & {} = (ab \ cos \ theta) ^ {2} + (- b \ sin \ theta) ^ {2} \\ c ^ {2} & {} = a ^ {2} -2ab \ cos \ theta + b ^ {2} \ cos ^ {2} \ theta + b ^ {2} \ sin ^ {2} \ theta \\ c ^ {2} & {} = a ^ {2} + b ^ {2} (\ sin ^ {2} \ theta + \ cos ^ {2} \ theta) -2ab \ cos \ theta \\ c ^ {2} & {} = a ^ {2} + b ^ {2} -2ab \ cos \ theta. \ end {alineado}}}

Una ventaja de esta prueba es que no requiere la consideración de diferentes casos para cuando el triángulo es agudo, correcto u obtuso.

Utilizando trigonometría [ editar ]

Fig. 5 - Un triángulo agudo con perpendicular.

Deje caer el perpendicular sobre el lado c para obtener (vea la Fig. 5)

$${\ displaystyle c = a \ cos \ beta + b \ cos \ alpha \ ,.}

(Esto sigue siendo cierto si α o β son obtusas, en cuyo caso la perpendicular cae fuera del triángulo). Multiplica a través de c para obtener

$${\ displaystyle c ^ {2} = ac \ cos \ beta + bc \ cos \ alpha.}

Teniendo en cuenta las otras perpendiculares obtenemos

$${\ displaystyle a ^ {2} = ac \ cos \ beta + ab \ cos \ gamma,}

$${\ displaystyle b ^ {2} = bc \ cos \ alpha + ab \ cos \ gamma.}

Sumando las dos últimas ecuaciones se obtiene.

$${\ displaystyle a ^ {2} + b ^ {2} = ac \ cos \ beta + bc \ cos \ alpha + 2ab \ cos \ gamma.}

Restando la primera ecuación de la última que tenemos

$${\ displaystyle a ^ {2} + b ^ {2} -c ^ {2} = - ac \ cos \ beta -bc \ cos \ alpha + ac \ cos \ beta + bc \ cos \ alpha + 2ab \ cos \ gamma}

lo que simplifica a

$${\ displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2ab \ cos \ gamma.}

Esta prueba utiliza la trigonometría porque trata los cosenos de los distintos ángulos como cantidades por derecho propio. Utiliza el hecho de que el coseno de un ángulo expresa la relación entre los dos lados que encierran ese ángulo en cualquier triángulo rectángulo. Otras pruebas (abajo) son más geométrica en que tratan una expresión como un cos gamma meramente como una etiqueta para la longitud de un segmento de línea determinada.

Muchas pruebas tratan los casos de ángulos obtusos y agudos γ por separado.

Usando el teorema de Pitágoras [ editar ]

Triángulo obtuso ABC con altura BH

Caso de un ángulo obtuso [ editar ]

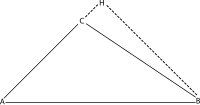
Euclid comprueba este teorema aplicando el teorema de Pitágoras a cada uno de los dos triángulos rectos en la figura que se muestra ( AHB y CHB ). Usando d para indicar el segmento de línea CH y h para la altura BH , triángulo AHB nos da

$${\ displaystyle c ^ {2} = (b + d) ^ {2} + h ^ {2},}

y el triángulo CHB da

$${\ displaystyle d ^ {2} + h ^ {2} = a ^ {2}.}

Expandiendo la primera ecuación da

$${\ displaystyle c ^ {2} = b ^ {2} + 2bd + d ^ {2} + h ^ {2}.}

Sustituyendo la segunda ecuación en esto, se puede obtener lo siguiente:

$${\ displaystyle c ^ {2} = a ^ {2} + b ^ {2} + 2bd.}

Esta es la Proposición 12 de Euclides del Libro 2 de los Elementos . ^[5] Para transformarlo en la forma moderna de la ley de los cosenos, tenga en cuenta que

$${\ displaystyle d = a \ cos (\ pi - \ gamma) = - a \ cos \ gamma.}

Caso de un ángulo agudo [ editar ]

La prueba de Euclides de su Proposición 13 se desarrolla siguiendo las mismas líneas que su prueba de la Proposición 12: aplica el teorema de Pitágoras a los dos triángulos rectángulos formados al colocar el perpendicular en uno de los lados que encierran el ángulo γ y utiliza el teorema del binomio para simplificar.

Fig. 6 - Una prueba corta que utiliza trigonometría para el caso de un ángulo agudo.

Otra prueba en el caso agudo [ editar ]

Usando más trigonometría, la ley de los cosenos puede deducirse usando el teorema de Pitágoras solo una vez . De hecho, al usar el triángulo rectángulo en el lado izquierdo de la Fig. 6, se puede mostrar que:

{\ displaystyle {\ begin {alineado} c ^ {2} & {} = (ba \ cos \ gamma) ^ {2} + (a \ sin \ gamma) ^ {2} \\ & {} = b ^ { 2} -2ab \ cos \ gamma + a ^ {2} \ cos ^ {2} \ gamma + a ^ {2} \ sin ^ {2} \ gamma \\ & {} = b ^ {2} + a ^ {2} -2ab \ cos \ gamma, \ end {alineado}}}

utilizando la identidad trigonométrica

$${\ displaystyle \ cos ^ {2} \ gamma + \ sin ^ {2} \ gamma = 1.}

Esta prueba necesita una ligera modificación si b < a cos ( γ ) . En este caso, el triángulo rectángulo al que se aplica el teorema de Pitágoras se mueve fuera del triángulo ABC . El único efecto que esto tiene en el cálculo es que la cantidad b - un cos ( γ ) se sustituye por un cos ( gamma ) - b . Como esta cantidad ingresa al cálculo solo a través de su cuadrado, el resto de la prueba no se ve afectado. Sin embargo, este problema solo ocurre cuando β es obtuso y puede evitarse reflejando el triángulo alrededor de la bisectriz deγ .

Con referencia a la Fig. 6, vale la pena señalar que si el ángulo opuesto al lado a es α, entonces:

$${\ displaystyle \ tan \ alpha = {\ frac {a \ sin \ gamma} {ba \ cos \ gamma}}.}

Esto es útil para el cálculo directo de un segundo ángulo cuando se dan dos lados y un ángulo incluido.

Usando el teorema de Ptolomeo [ editar ]

Prueba de ley de cosenos usando el teorema de Ptolomeo

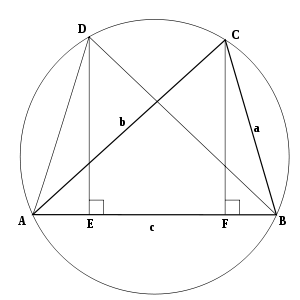
Refiriéndose al diagrama, el triángulo ABC con los lados AB= c , BC = a y AC = b se dibuja dentro de su circuncírculo como se muestra. El triángulo ABD se construye congruente con el triángulo ABC con AD = BC y BD = AC . Las perpendiculares de D y C se encuentran con la base AB en E y F respectivamente. Entonces:

{\ displaystyle {\ begin {alineado} & BF = AE = BC \ cos {\ hat {B}} = a \ cos {\ hat {B}} \\ Rightarrow \ & DC = EF = AB-2BF = c-2a \ cos {\ hat {B}}. \ end {alineado}}}

Ahora, la ley de los cosenos se traduce en una aplicación directa del teorema de Ptolomeo al cuadrilátero cíclico ABCD :

{\ displaystyle {\ begin {alineado} & AD \ times BC + AB \ times DC = AC \ times BD \\\ Rightarrow \ & a ^ {2} + c (c-2a \ cos {\ hat {B}}) = b ^ {2} \\\ Rightarrow \ & a ^ {2} + c ^ {2} -2ac \ cos {\ hat {B}} = b ^ {2}. \ end {alineado}}}

Claramente, si el ángulo B es correcto , entonces ABCD es un rectángulo y la aplicación del teorema de Ptolomeo produce el teorema de Pitágoras :

$${\ displaystyle a ^ {2} + c ^ {2} = b ^ {2}. \ quad}

Comparando áreas [ editar ]

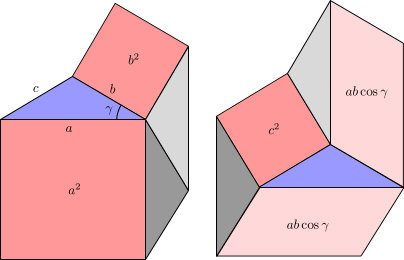
También se puede probar la ley de los cosenos mediante el cálculo de áreas . El cambio de signo a medida que el ángulo γ se vuelve obtuso hace necesaria una distinción de casos.

Recordar que

• a ² , b ² y c ² son las áreas de los cuadrados con los lados a , b y c , respectivamente;
• si γ es agudo, entonces ab cos γ es el área del paralelogramo con los lados a y b que forman un ángulo de γ ′ = π/2 - γ ;
• si γ es obtuso, y entonces cos γ es negativo, entonces - ab cos γ es el área del paralelogramo con los lados ay b que forman un ángulo de γ ′ = γ - π/2 .

Fig. 7a - Prueba de la ley de cosenos para el ángulo agudo γ mediante "corte y pegado".

Caso agudo. La Figura 7a muestra un heptágono cortado en trozos más pequeños (de dos maneras diferentes) para proporcionar una prueba de la ley de los cosenos. Las diferentes piezas son

• en rosa, las áreas a ² , b ² a la izquierda y las áreas 2 ab cos γ y c ² a la derecha;
• en azul, el triángulo ABC , a la izquierda y a la derecha;
• en gris, triángulos auxiliares, todos congruentes con ABC , un número igual (es decir, 2) tanto a la izquierda como a la derecha.

La igualdad de áreas a la izquierda y a la derecha da

$${\ displaystyle \, a ^ {2} + b ^ {2} = c ^ {2} + 2ab \ cos \ gamma \ ,.}

Fig. 7b: Prueba de la ley de cosenos para el ángulo obtuso γ mediante "corte y pegado".

Caso obtuso. La Figura 7b corta un hexágono de dos maneras diferentes en pedazos más pequeños, lo que proporciona una prueba de la ley de los cosenos en el caso de que el ángulo γsea ​​obtuso. Tenemos

• en rosa, las áreas a ² , b ² y −2 ab cos γ a la izquierda y c ² a la derecha;
• en azul, el triángulo ABC dos veces, a la izquierda, así como a la derecha.

La igualdad de áreas a la izquierda y a la derecha da

$${\ displaystyle \, a ^ {2} + b ^ {2} -2ab \ cos (\ gamma) = c ^ {2}.}

La prueba rigurosa deberá incluir pruebas de que varias formas son congruentes y, por lo tanto, tienen el mismo área. Esto usará la teoría de los triángulos congruentes .

Usando la geometría del círculo [ editar ]

Usando la geometría del círculo , es posible dar una prueba más geométrica que usando solo el teorema de Pitágoras . Se evitan las manipulaciones algebraicas (en particular el teorema binomial ).

Fig. 8a - El triángulo ABC (rosa), un círculo auxiliar (azul claro) y un triángulo derecho auxiliar (amarillo)

Caso de ángulo agudo γ , donde a > 2 b cos γ . Coloque la perpendicular de A en a = BC , creando un segmento de línea de longitud b cos γ . Duplique el triángulo rectángulo para formar el triángulo isósceles ACP . Construir el círculo con centro A y el radio b , y su tangente h = BHa través de B . La tangente hforma un ángulo recto con el radio b ( Elementos de Euclides : Libro 3, Proposición 18; o vea aquí ), por lo que el triángulo amarillo en la Figura 8 es correcto. Aplicar el teorema de Pitágoras para obtener

$${\ displaystyle c ^ {2} = b ^ {2} + h ^ {2}.}

Luego use el teorema de la secante tangente ( Elementos de Euclides : Libro 3, Proposición 36), que dice que el cuadrado en la tangente a través de un punto B fuera del círculo es igual al producto de los dos segmentos de líneas (de B ) creados por cualquier secante del círculo a través de b . En el presente caso: BH ² = BC · BP , o

$${\ displaystyle h ^ {2} = a (a-2b \ cos \ gamma).}

Sustituir en la ecuación anterior da la ley de cosenos:

$${\ displaystyle c ^ {2} = b ^ {2} + a (a-2b \ cos \ gamma).}

Tenga en cuenta que h ² es la potencia del punto B con respecto al círculo. El uso del teorema de Pitágoras y el teorema de la secante tangente se puede reemplazar por una sola aplicación del poder del teorema de un punto .

Fig. 8b - El triángulo ABC (rosa), un círculo auxiliar (azul claro) y dos triángulos rectos auxiliares (amarillo)

Caso de ángulo agudo γ , donde a <2 font="" nbsp="">b cos γ . Coloque la perpendicular de A en a = BC , creando un segmento de línea de longitud b cos γ . Duplique el triángulo rectángulo para formar el triángulo isósceles ACP . Construya el círculo con el centro A y el radio b , y una cuerda a través de B perpendicular a c = AB , la mitad de la cual esh = BH . Aplicar el teorema de Pitágoras para obtener

$${\ displaystyle b ^ {2} = c ^ {2} + h ^ {2}.}

Ahora use el teorema de acorde ( Elementos de Euclides : Libro 3, Proposición 35), que dice que si dos acordes se intersecan, el producto de los dos segmentos de línea obtenidos en un acorde es igual al producto de los dos segmentos de línea obtenidos en el otro acorde . En el presente caso: BH ² = BC · BP , o

$${\ displaystyle h ^ {2} = a (2b \ cos \ gamma -a).}

Sustituir en la ecuación anterior da la ley de cosenos:

$${\ displaystyle b ^ {2} = c ^ {2} + a (2b \ cos \ gamma -a) \ ,.}

Tenga en cuenta que la potencia del punto B con respecto al círculo tiene el valor negativo - h ² .

Fig. 9 - Prueba de la ley de cosenos usando el poder de un teorema de punto.

Caso de ángulo obtuso γ . Esta prueba utiliza la potencia de un teorema de puntos directamente, sin los triángulos auxiliares obtenidos al construir una tangente o un acorde. Construir un círculo con el centro B y el radio de una (véase la figura 9), que se cruza con la secante a través de A y C en C y K . La potencia del punto A con respecto al círculo es igual a AB ² - BC ² y AC · AK . Por lo tanto,

{\ displaystyle {\ begin {alineado} c ^ {2} -a ^ {2} & {} = b (b + 2a \ cos (\ pi - \ gamma)) \\ & {} = b (b-2a \ cos \ gamma), \ end {alineado}}}

Que es la ley de los cosenos.

Usando medidas algebraicas para segmentos de línea (permitiendo números negativos como longitudes de segmentos), el caso del ángulo obtuso ( CK > 0 ) y el ángulo agudo ( CK <0 font=""> ) se pueden tratar simultáneamente.

Usando la ley de los senos [ editar ]

Al usar la ley de los senos y al saber que los ángulos de un triángulo deben sumar 180 grados, tenemos el siguiente sistema de ecuaciones (las tres incógnitas son los ángulos):

$${\ displaystyle {\ frac {c} {\ sin \ gamma}} = {\ frac {b} {\ sin \ beta}},}

$${\ displaystyle {\ frac {c} {\ sin \ gamma}} = {\ frac {a} {\ sin \ alpha}},}

$${\ displaystyle \ alpha + \ beta + \ gamma = \ pi.}

Luego, al utilizar la tercera ecuación del sistema, obtenemos un sistema de dos ecuaciones en dos variables:

$${\ displaystyle {\ frac {c} {\ sin \ gamma}} = {\ frac {b} {\ sin (\ alpha + \ gamma)}},}

$${\ displaystyle {\ frac {c} {\ sin \ gamma}} = {\ frac {a} {\ sin \ alpha}},}

donde hemos utilizado la propiedad trigonométrica de que el seno de un ángulo suplementario es igual al seno del ángulo.

Uso de la identidad (ver identidades de suma y diferencia de ángulo )

$${\ displaystyle \ sin (\ alpha + \ gamma) = \ sin \ alpha \ cos \ gamma + \ sin \ gamma \ cos \ alpha}

lleva a

$${\ displaystyle c (\ sin \ alpha \ cos \ gamma + \ sin \ gamma \ cos \ alpha) = b \ sin \ gamma,}

$${\ displaystyle c \ sin \ alpha = a \ sin \ gamma.}

Al dividir todo el sistema por cos γ , tenemos:

$${\ displaystyle c (\ sin \ alpha + \ tan \ gamma \ cos \ alpha) = b \ tan \ gamma,}

$${\ displaystyle {\ frac {c \ sin \ alpha} {\ cos \ gamma}} = a \ tan \ gamma,}

$${\ displaystyle {\ frac {c ^ {2} \ sin ^ {2} \ alpha} {\ cos ^ {2} \ gamma}} = a ^ {2} \ tan ^ {2} \ gamma.}

Por lo tanto, a partir de la primera ecuación del sistema, podemos obtener

$${\ displaystyle {\ frac {c \ sin \ alpha} {bc \ cos \ alpha}} = \ tan \ gamma}

Sustituyendo esta expresión en la segunda ecuación y usando

$${\ displaystyle 1+ \ tan ^ {2} \ gamma = {\ frac {1} {\ cos ^ {2} \ gamma}}}

Podemos obtener una ecuación con una variable:

$${\ displaystyle c ^ {2} \ sin ^ {2} \ alpha \ left (1 + {\ frac {c ^ {2} \ sin ^ {2} \ alpha} {(bc \ cos \ alpha) ^ {2 }}} \ right) = a ^ {2} \ cdot {\ frac {c ^ {2} \ sin ^ {2} \ alpha} {(bc \ cos \ alpha) ^ {2}}}}

Al multiplicar por ( b - c cos α ) ² , podemos obtener la siguiente ecuación:

$${\ displaystyle (bc \ cos \ alpha) ^ {2} + c ^ {2} \ sin ^ {2} \ alpha = a ^ {2}.}

Esto implica

$${\ displaystyle b ^ {2} -2bc \ cos \ alpha + c ^ {2} \ cos ^ {2} \ alpha + c ^ {2} \ sin ^ {2} \ alpha = a ^ {2}.}

Recordando la identidad de Pitágoras , obtenemos la ley de los cosenos:

$${\ displaystyle a ^ {2} = b ^ {2} + c ^ {2} -2bc \ cos \ alpha.}

Caso isósceles [ editar ]

Cuando a = b , es decir, cuando el triángulo es isósceles con los dos lados que inciden en el ángulo γ igual, la ley de los cosenos se simplifica significativamente. Es decir, debido a que ² + b ² = 2 a ² = 2 ab , la ley de los cosenos se convierte en

$${\ displaystyle \ cos \ gamma = 1 - {\ frac {c ^ {2}} {2a ^ {2}}}}

o

$${\ displaystyle c ^ {2} = 2a ^ {2} (1- \ cos \ gamma).}

Analógica para tetraedros [ editar ]

Una declaración análoga comienza tomando α , β , γ , δ como las áreas de las cuatro caras de un tetraedro . Denota los ángulos diédricos por$${\ displaystyle {\ widehat {\ beta \ gamma}}}Entonces ^[6]

$${\ displaystyle \ alpha ^ {2} = \ beta ^ {2} + \ gamma ^ {2} + \ delta ^ {2} -2 \ left (\ beta \ gamma \ cos \ left ({\ widehat {\ beta \ gamma}} \ right) + \ gamma \ delta \ cos \ left ({\ widehat {\ gamma \ delta}} \ right) + \ delta \ beta \ cos \ left ({\ widehat {\ delta \ beta}} \bien bien).}

Versión adecuada para pequeños ángulos [ editar ]

Cuando el ángulo, γ , es pequeño y los lados adyacentes, a y b , tienen una longitud similar, el lado derecho de la forma estándar de la ley de los cosenos puede perder mucha precisión con respecto a la pérdida numérica de importancia . En situaciones donde esta es una preocupación importante, una versión matemáticamente equivalente de la ley de los cosenos, similar a la fórmula de haversine , puede resultar útil:

{\ displaystyle {\ begin {alineado} c ^ {2} & = (ab) ^ {2} + 4ab \ sin ^ {2} \ left ({\ frac {\ gamma} {2}} \ right) \\ & = (ab) ^ {2} + 4ab \ operatorname {haversin} (\ gamma). \ end {alineado}}}

En el límite de un ángulo infinitesimal, la ley de los cosenos se degenera en la fórmula de longitud de arco circular , c = a γ .

En geometría esférica e hiperbólica [ editar ]

Artículos principales: Ley esférica de los cosenos y Ley hiperbólica de los cosenos.

Triángulo esférico resuelto por la ley de los cosenos.

Versiones similares a la ley de cosenos para el plano euclidiano también se sostienen en una esfera unitaria y en un plano hiperbólico. En geometría esférica , un triángulo se define por tres puntos u , v y w en la esfera unitaria, y los arcos de círculos grandes que conectan esos puntos. Si estos grandes círculos forman los ángulos A , B y C con los lados opuestos a , b , c , entonces la ley esférica de los cosenos afirma que ambas de las siguientes relaciones son válidas:

{\ displaystyle {\ begin {alineado} \ cos a & = \ cos b \ cos c + \ sin b \ sin c \ cos A \\ cos porque & = - \ cos B \ cos C + \ sin B \ sin C \ cos a . \ end {alineado}}}

En la geometría hiperbólica , un par de ecuaciones se conocen colectivamente como la ley hiperbólica de los cosenos . El primero es

$${\ displaystyle \ cosh a = \ cosh b \ cosh c- \ sinh b \ sinh c \ cos A}

donde sinh y cosh son el seno y el coseno hiperbólicos , y el segundo es

$${\ displaystyle \ cos A = - \ cos B \ cos C + \ sin B \ sin C \ cosh a.}

Como en la geometría euclidiana, se puede usar la ley de los cosenos para determinar los ángulos A , B , C apartir del conocimiento de los lados a , b , c . A diferencia de la geometría euclidiana, lo contrario también es posible en ambos modelos no euclidianos: los ángulos A , B , C determinan los lados a , b , c .

Fórmula unificada para superficies de curvatura constante [ editar ]

Definiendo dos funciones $${\ displaystyle \ cos _ {R}} y $${\ displaystyle \ sin _ {R}} como

$${\ displaystyle \ cos _ {R} (x) = \ cos (x / R) \ quad} y $${\ displaystyle \ quad \ sin _ {R} (x) = R \ cdot \ sin (x / R)}

Permite unificar las fórmulas de plano , esfera y pseudosfera en:

$${\ displaystyle \ cos _ {R} (BC) = \ cos _ {R} (AB) \ cdot \ cos _ {R} (AC) + {\ frac {1} {R ^ {2}}} \ sin _ {R} (AB) \ cdot \ sin _ {R} (AC) \ cdot \ cos ({\ widehat {BAC}}).}

En esta notación $${\ displaystyle R}es un número complejo , que representa el radio de curvatura de la superficie .

• por $${\ displaystyle R \ in \ mathbb {R}}La superficie es una esfera de radio.$${\ displaystyle R}, y su curvatura constante es igual a $${\ displaystyle 1 / R ^ {2};}

• para $${\ displaystyle R = iR '\ colon R' \ in \ mathbb {R}} La superficie es una pseudosfera de radio (imaginario).$${\ displaystyle R,}con curvatura constante igual a$${\ displaystyle 1 / R ^ {2} = - 1 / R '^ {2};}

• para $${\ displaystyle R \ to \ infty} : la superficie tiende a un plano euclidiano , con curvatura cero constante.

Verificación de la fórmula para geometría no euclidiana

En los dos primeros casos, $${\ displaystyle \ cos _ {R}} y $${\ displaystyle \ sin _ {R}}Están bien definidos en todo el plano complejo para todos.$${\ displaystyle R \ neq 0}, y recuperar los resultados anteriores es sencillo.

Por lo tanto, para una esfera de radio. $${\ displaystyle 1}

$${\ displaystyle \ cos (BC) = \ cos (AB) \ cdot \ cos (AC) + \ sin (AB) \ cdot \ sin (AC) \ cdot \ cos ({\ widehat {BAC}})}.

Asimismo, para una pseudosfera de radio. $${\ displaystyle i}

$${\ displaystyle \ cosh (BC) = \ cosh (AB) \ cdot \ cosh (AC) - \ sinh (AB) \ cdot \ sinh (AC) \ cdot \ cos ({\ widehat {BAC}}).}

En efecto, $${\ displaystyle \ cosh (x) = \ cos (x / i)} y $${\ displaystyle \ sinh (x) = i \ cdot \ sin (x / i).}

Verificando la fórmula en el límite de la geometría euclidiana.

En el plano euclidiano, se deben calcular los límites apropiados para la ecuación anterior:

$${\ displaystyle \ cos _ {R} (x) = \ cos (x / R) = 1 - {\ frac {1} {2}} \ cdot {\ frac {x ^ {2}} {R ^ {2 }}} + o \ left ({\ frac {1} {R ^ {4}}} \ right)}

y

$${\ displaystyle \ sin _ {R} (x) = R \ cdot \ sin (x / R) = x + o \ left ({\ frac {1} {R ^ {3}}} \ right)}.

Aplicando esto a la fórmula general para un finito. $${\ displaystyle R} rendimientos

{\ displaystyle {\ begin {alineado} 1 - {\ frac {BC ^ {2}} {2R ^ {2}}} + o \ left ({\ frac {1} {R ^ {4}}} \ right ) & = \ left (1 - {\ frac {AB ^ {2}} {2R ^ {2}}} + o \ left ({\ frac {1} {R ^ {4}}} \ right) \ right ) \ cdot \ left (1 - {\ frac {AC ^ {2}} {2R ^ {2}}} + o \ left ({\ frac {1} {R ^ {4}}} \ right) \ right ) + \\ & + {\ frac {1} {R ^ {2}}} \ left (AB + o \ left ({\ frac {1} {R ^ {3}}} \ right) \ right) \ right) \ cdot \ izquierda (AC + o \ izquierda ({\ frac {1} {R ^ {3}}} \ derecha) \ derecha) \ cdot \ cos ({\ widehat {BAC}}) \ end {alineado}}}

Recopilación de términos, multiplicando con $${\ displaystyle -2R ^ {2},} y tomando $${\ displaystyle R \ to \ infty} produce la fórmula esperada:

$${\ displaystyle BC ^ {2} = AB ^ {2} + AC ^ {2} -2 \ cdot AB \ cdot AC \ cdot \ cos ({\ widehat {BAC}}).}