TRIGONOMETRÍA

 ley de los cotangentes ^[1] es una relación entre las longitudes de los lados de un triángulo y los cotangentes de las mitades de los tres ángulos.

Así como tres cantidades cuya igualdad se expresa por la ley de los senos son iguales al diámetro del círculo circunscrito del triángulo (o a su recíproco, dependiendo de cómo se expresa la ley), así también la ley de los cotangentes relaciona el radio de El círculo inscrito de un triángulo (el inradio ) a sus lados y ángulos.

Un triángulo, que muestra el "incircle" y la división de los lados. Las bisectrices de ángulo se encuentran en el incentivo , que es el centro del incircle .

Declaración [ editar ]

Usando las notaciones habituales para un triángulo (vea la figura en la parte superior derecha), donde a , b , c son las longitudes de los tres lados, A , B , C son los vértices opuestos a esos tres lados respectivos, α , β , γ son los ángulos correspondientes en esos vértices, s es el semiperímetro, es decir, s = a + b + c/2 , y r es el radio del círculo inscrito, la ley de los cotangentes establece que

$${\ displaystyle {\ frac {\ cot \ left ({\ tfrac {\ alpha} {2}} \ right)} {sa}} = {\ frac {\ cot \ left ({\ tfrac {\ beta} {2 }} \ right)} {sb}} = {\ frac {\ cot \ left ({\ tfrac {\ gamma} {2}} \ right)} {sc}} = {\ frac {1} {r}} \,}

y además que el inradio está dado por

$${\ displaystyle r = {\ sqrt {\ frac {(sa) (sb) (sc)} {s}}} \ ,.}

Prueba [ editar ]

En la figura superior, los puntos de tangencia del incirculo con los lados del triángulo rompen el perímetro en 6 segmentos, en 3 pares. En cada par los segmentos son de igual longitud. Por ejemplo, los 2 segmentos adyacentes al vértice A son iguales. Si elegimos un segmento de cada par, su suma será el semiperímetro s . Un ejemplo de esto son los segmentos que se muestran en color en la figura. Los dos segmentos que componen la línea roja se suman a una , por lo que el segmento de azul debe ser de longitud s - una . Obviamente, los otros cinco segmentos también deben tener las longitudes s - a , s - b , o s - c, como se muestra en la figura inferior.

Mediante la inspección de la figura, utilizando la definición de la función cotangente, tenemos

$${\ displaystyle \ cot \ left ({\ frac {\ alpha} {2}} \ right) = {\ frac {sa} {r}} \,}

y de manera similar para los otros dos ángulos, demostrando la primera afirmación.

Para la segunda, la fórmula inradius, partimos de la fórmula de suma general :

$${\ displaystyle \ cot (u + v + w) = {\ frac {\ cot u + \ cot v + \ cot w- \ cot u \ cot v \ cot w} {1- \ cot u \ cot v- \ cot v \ cot w- \ cot w \ cot u}}.}

Aplicando a la cuna ( α/2 + β/2 + γ/2) = cot π/2 = 0 , obtenemos:

$${\ displaystyle \ cot \ left ({\ frac {\ alpha} {2}} \ right) \ cot \ left ({\ frac {\ beta} {2}} \ right) \ cot \ left ({\ frac { \ gamma} {2}} \ derecha) = \ cot \ left ({\ frac {\ alpha} {2}} \ right) + \ cot \ left ({\ frac {\ beta} {2}} \ right) + \ cot \ left ({\ frac {\ gamma} {2}} \ right).}

(Esta es también la identidad triple cotangente )

Sustituyendo los valores obtenidos en la primera parte, obtenemos:

$${\ displaystyle {\ frac {(sa)} {r}} {\ frac {(sb)} {r}} {\ frac {(sc)} {r}} = {\ frac {sa} {r}} + {\ frac {sb} {r}} + {\ frac {sc} {r}} = {\ frac {3s-2s} {r}} = {\ frac {s} {r}}.

Si se multiplica por r ³/s, se obtiene el valor de r ² , lo que demuestra la segunda afirmación.

Algunas pruebas usando la ley de cotangentes [ editar ]

Una serie de otros resultados se pueden derivar de la ley de los cotangentes.

• Fórmula de Heron . Tenga en cuenta que el área del triángulo ABC también se divide en 6 triángulos más pequeños, también en 3 pares, con los triángulos en cada par que tienen la misma área. Por ejemplo, los dos triángulos cerca de vértice A , siendo los triángulos rectángulos de anchura s - a y altura r , tienen cada uno un área de 1/2 r ( s - una ) . Entonces, esos dos triángulos juntos tienen un área de r ( s - a ) , y el área S de todo el triángulo es, por lo tanto,

{\ displaystyle {\ begin {alineado} S & = r (sa) + r (sb) + r (sc) = r {\ bigl (} 3s- (a + b + c) {\ bigr)} = r (3s -2s) = rs \\ [8pt] \ end {alineado}}}

Esto da el resultado.

S = √ s ( s - a ) ( s - b ) ( s - c )

según sea necesario.

• Primera fórmula de Mollweide . A partir de la fórmula de adición y la ley de cotangentes tenemos

$${\ displaystyle {\ frac {\ sin \ left ({\ tfrac {\ alpha} {2}} - {\ tfrac {\ beta} {2}} \ right)} {\ sin \ left ({\ tfrac {\ alpha} {2}} + {\ tfrac {\ beta} {2}} \ right)}} = {\ frac {\ cot \ left ({\ tfrac {\ beta} {2}} \ right) - \ cot \ left ({\ tfrac {\ alpha} {2}} \ right)} {\ cot \ left ({\ tfrac {\ beta} {2}} \ right) + \ cot \ left ({\ tfrac {\ alpha } {2}} \ derecha)}} = {\ frac {ab} {2s-ab}}.}

Esto da el resultado.

$${\ displaystyle {\ dfrac {ab} {c}} = {\ dfrac {\ sin \ left ({\ tfrac {\ alpha} {2}} - {\ tfrac {\ beta} {2}} \ right)} {\ cos \ left ({\ tfrac {\ gamma} {2}} \ right)}}}

según sea necesario.

• La segunda fórmula de Mollweide . A partir de la fórmula de adición y la ley de cotangentes tenemos

{\ displaystyle {\ begin {alineado} & {\ frac {\ cos \ left ({\ tfrac {\ alpha} {2}} - {\ tfrac {\ beta} {2}} \ right)} {\ cos \ izquierda ({\ tfrac {\ alpha} {2}} + {\ tfrac {\ beta} {2}} \ derecha)}} = {\ frac {\ cot \ left ({\ tfrac {\ alpha} {2} } \ right) \ cot \ left ({\ tfrac {\ beta} {2}} \ right) +1} {\ cot \ left ({\ tfrac {\ alpha} {2}} \ right) \ cot \ left ({\ tfrac {\ beta} {2}} \ right) -1}} \\ [6pt] = {} & {\ frac {\ cot \ left ({\ tfrac {\ alpha} {2}} \ right ) + \ cot \ left ({\ tfrac {\ beta} {2}} \ right) +2 \ cot \ left ({\ tfrac {\ gamma} {2}} \ right)} {\ cot \ left ({ \ tfrac {\ alpha} {2}} \ right) + \ cot \ left ({\ tfrac {\ beta} {2}} \ right)}} = {\ frac {4s-ab-2c} {2s-ab }}. \ end {alineado}}}

Aquí, se requiere un paso adicional para transformar un producto en una suma, de acuerdo con la fórmula de suma / producto.

Esto da el resultado.

$${\ displaystyle {\ dfrac {b + a} {c}} = {\ dfrac {\ cos \ left ({\ tfrac {\ alpha} {2}} - {\ tfrac {\ beta} {2}} \ right )} {\ sin \ left ({\ tfrac {\ gamma} {2}} \ right)}}}

según sea necesario.

• La ley de las tangentes también se puede derivar de esto ( Silvester 2001 , p. 99).

la ley de los senos , ley de los senos , fórmula sinusoidal , o de reglas sinusoidal es una ecuación que relaciona las longitudes de los lados de un triángulo (cualquier forma) a los senos de sus ángulos. De acuerdo con la ley,

$${\ displaystyle {\ frac {a} {\ sin A}} \, = \, {\ frac {b} {\ sin B}} \, = \, {\ frac {c} {\ sin C}} \ , = \, d,}

donde a , b y c son las longitudes de los lados de un triángulo, y A , B y C son los ángulos opuestos (vea la figura a la derecha), mientras que des el diámetro del circuncírculo del triángulo . Cuando no se usa la última parte de la ecuación, la ley a veces se establece utilizando los recíprocos;

$${\ displaystyle {\ frac {\ sin A} {a}} \, = \, {\ frac {\ sin B} {b}} \, = \, {\ frac {\ sin C} {c}}. }

La ley de los senos se puede usar para calcular los lados restantes de un triángulo cuando se conocen dos ángulos y un lado, una técnica conocida como triangulación . También se puede utilizar cuando se conocen dos lados y uno de los ángulos no cerrados. En algunos de estos casos, el triángulo no está determinado únicamente por estos datos (llamado el caso ambiguo ) y la técnica ofrece dos valores posibles para el ángulo incluido.

La ley de los senos es una de las dos ecuaciones trigonométricas que se aplican comúnmente para encontrar longitudes y ángulos en los triángulos escalenos, siendo la otra la ley de los cosenos .

La ley de los senos se puede generalizar a dimensiones más altas en superficies con curvatura constante.

Un triángulo etiquetado con los componentes de la ley de los senos. Capital A , B y C son los ángulos, y minúscula una , b , c son los lados opuestos ellos. ( Un opuesto A , etc.)

Prueba [ editar ]

El área T de cualquier triángulo puede escribirse como la mitad de su base por su altura. Al seleccionar un lado del triángulo como base, la altura del triángulo con relación a esa base se calcula como la longitud de otro lado por el seno del ángulo entre el lado elegido y la base. Por lo tanto, dependiendo de la selección de la base, el área del triángulo se puede escribir como:

$${\ displaystyle T = {\ frac {1} {2}} b (c \ sin A) = {\ frac {1} {2}} c (a \ sin B) = {\ frac {1} {2} } a (b \ sin C) \ ,.}

Multiplicando estos por 2/abc da

$${\ displaystyle {\ frac {2T} {abc}} = {\ frac {\ sin A} {a}} = {\ frac {\ sin B} {b}} = {\ frac {\ sin C} {c }} \ ,.}

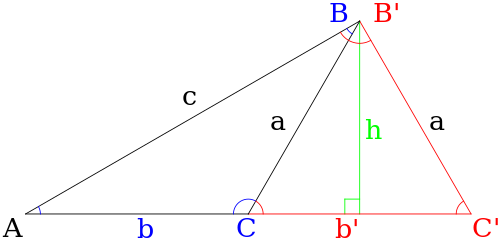
El ambiguo caso de la solución triangular [ editar ]

Cuando se usa la ley de los senos para encontrar un lado de un triángulo, ocurre un caso ambiguo cuando se pueden construir dos triángulos separados a partir de los datos proporcionados (es decir, hay dos soluciones posibles diferentes para el triángulo). En el caso mostrado abajo, son los triángulos ABC y AB′C ′ .

Dado un triángulo general, las siguientes condiciones deben cumplirse para que el caso sea ambiguo:

• La única información conocida sobre el triángulo es el ángulo A y los lados a y c .
• El ángulo A es agudo (es decir, A <90 font="">
• El lado a es más corto que el lado c (es decir, a < c ).
• El lado a es más largo que la altitud h desde el ángulo B , donde h = c sin A (es decir, a > h ).

Si todas las condiciones anteriores son verdaderas, entonces cada uno de los ángulos C y C ′ produce un triángulo válido, lo que significa que ambos de los siguientes son verdaderos:

$${\ displaystyle C '= \ arcsin {\ frac {c \ sin A} {a}} {\ text {o}} C = \ pi - \ arcsin {\ frac {c \ sin A} {a}}.}

A partir de ahí se encuentra el correspondiente B y B o B ' y B' si se requiere, en donde b es la parte delimitada por los ángulos A y C y B ' delimitada por una y C' .

Sin más información, es imposible decidir cuál es el triángulo que se solicita.

Ejemplos [ editar ]

Los siguientes son ejemplos de cómo resolver un problema usando la ley de los senos.

Ejemplo 1 [ editar ]

Dado: lado a = 20 , lado c = 24 y ángulo C = 40 ° . Se desea el ángulo A

Usando la ley de los senos, concluimos que

$${\ displaystyle {\ frac {\ sin A} {20}} = {\ frac {\ sin 40 ^ {\ circ}} {24}}.}

$${\ displaystyle A = \ arcsin \ left ({\ frac {20 \ sin 40 ^ {\ circ}} {24}} \ right) \ approx 32.39 ^ {\ circ}.}

Tenga en cuenta que la solución potencial A = 147.61 ° se excluye porque eso daría necesariamente A + B + C > 180 ° .

Ejemplo 2 [ editar ]

Si las longitudes de los dos lados del triángulo a y b son iguales a x , el tercer lado tiene la longitud c , y los ángulos opuestos a los lados de las longitudes a , b y c son A , B y C respectivamente, entonces

{\ displaystyle {\ begin {alineado} & A = B = {\ frac {180 ^ {\ circ} -C} {2}} = 90 ^ {\ circ} - {\ frac {C} {2}} \\ [6pt] & \ sin A = \ sin B = \ sin \ izquierda (90 ^ {\ circ} - {\ frac {C} {2}} \ derecha) = \ cos \ izquierda ({\ frac {C} { 2}} \ derecha) \\ [6pt] & {\ frac {c} {\ sin C}} = {\ frac {a} {\ sin A}} = {\ frac {x} {\ cos \ left ( {\ frac {C} {2}} \ right)}} \\ [6pt] & {\ frac {c \ cos \ left ({\ frac {C} {2}} \ right)} {\ sin C} } = x \ end {alineado}}}

Relación con la circunferencia circunscrita [ editar ]

En la identidad

$${\ displaystyle {\ frac {a} {\ sin A}} = {\ frac {b} {\ sin B}} = {\ frac {c} {\ sin C}},}

el valor común de las tres fracciones es en realidad el diámetro del circuncírculo del triángulo que se remonta a Ptolomeo . ^[2] [3]

Derivando la relación de la ley del seno igual al diámetro de la circunscripción. Tenga en cuenta que el triángulo ADB pasa por el centro del círculo circunscrito.

Prueba [ editar ]

Como se muestra en la figura, que haya un círculo con inscripciones$${\ displaystyle \ bigtriangleup ABC} y otra inscrita $${\ displaystyle \ bigtriangleup ADB}que pasa a través del centro del círculo O . los$${\ displaystyle \ angle AOD}tiene un ángulo central de$${\ displaystyle 180 ^ {\ circ}} y por lo tanto $${\ displaystyle \ angle ABD = 90 ^ {\ circ}}. Ya que$${\ displaystyle \ bigtriangleup ABD} es un triángulo rectángulo,

$${\ displaystyle \ sin D = {\ frac {\ text {opuesto}} {\ text {hypotenuse}}} = {\ frac {c} {2R}},

dónde $${\ displaystyle R}es el radio del círculo que circunscribe al triángulo. ^[3] ángulos$${\ displaystyle \ angle C} y $${\ displaystyle \ angle D}tienen el mismo ángulo central por lo que son los mismos:$${\ displaystyle \ angle C = \ angle D}. Por lo tanto,

$${\ displaystyle \ sin D = \ sin C = {\ frac {c} {2R}}.}

Reorganizar los rendimientos.

$${\ displaystyle 2R = {\ frac {c} {\ sin C}}.}

Repitiendo el proceso de creación. $${\ displaystyle \ bigtriangleup ADB} con otros puntos da

$${\ displaystyle {\ frac {a} {\ sin A}} = {\ frac {b} {\ sin B}} = {\ frac {c} {\ sin C}} = 2R.}

Relación con el área del triángulo [ editar ]

El área de un triángulo está dada por $${\ displaystyle T = {\ frac {1} {2}} ab \ sin \ theta}, dónde $${\ displaystyle \ theta}es el ángulo encerrado por los lados de las longitudes a y b . Sustituyendo la ley del seno en esta ecuación da

$${\ displaystyle T = {\ frac {1} {2}} ab \ cdot {\ frac {c} {2R}}.

Tomando $${\ displaystyle R}como el radio de circunscripción, ^[4]

$${\ displaystyle T = {\ frac {abc} {4R}}.}

También se puede demostrar que esta igualdad implica

{\ displaystyle {\ begin {alineado} {\ frac {abc} {2T}} & = {\ frac {abc} {2 {\ sqrt {s (sa) (sb) (sc)}}}} \\ [ 6pt] & = {\ frac {2abc} {\ sqrt {{(a ^ {2} + b ^ {2} + c ^ {2})} ^ {2} -2 (a ^ {4} + b ^ {4} + c ^ {4})}}}, \ end {alineado}}}

donde T es el área del triángulo y s es el semiperímetro $${\ displaystyle s = {\ frac {a + b + c} {2}}.}

La segunda igualdad anterior se simplifica fácilmente a la fórmula de Heron para el área.

La regla del signo también se puede usar para derivar la siguiente fórmula para el área del triángulo: Denota la semi-suma de los senos de los ángulos como $${\ displaystyle S = {\ tfrac {(sinA) + (sinB) + (sinC)} {2}}}, tenemos ^[5]

$${\ displaystyle T = D ^ {2} {\ sqrt {S (S- \ sin A) (S- \ sin B) (S- \ sin C)}}}

donde D es el diámetro del circuncírculo:$${\ displaystyle D = 2R = {\ tfrac {a} {\ sin A}} = {\ tfrac {b} {\ sin B}} = {\ tfrac {c} {\ sin C}}.}

Curvatura [ editar ]

La ley de los senos toma una forma similar en presencia de curvatura.

Caso esférico [ editar ]

En el caso esférico, la fórmula es:

$${\ displaystyle {\ frac {\ sin A} {\ sin \ alfa}} = {\ frac {\ sin B} {\ sin \ beta}} = {\ frac {\ sin C} {\ sin \ gamma}} .}

Aquí, α , β y γ son los ángulos en el centro de la esfera subtendidos por los tres arcos del triángulo de superficie esférica a , b y c , respectivamente. A , B y C son los ángulos de la superficie opuestos a sus respectivos arcos.

Prueba de vectores [ editar ]

Considere una esfera unitaria con tres vectores unitarios OA , OB y OCdibujados desde el origen hasta los vértices del triángulo. Por lo tanto, los ángulos α , β y γ son los ángulos a , b y c , respectivamente. El arco BCsubtiende un ángulo de magnitud a en el centro. Introduzca una base cartesiana con OA a lo largo del eje z y OB en el plano xz haciendo un ángulo c con el eje z . El vector OCproyectos a EN en la xy un plano y el ángulo entre EN y el x eje x es A . Por lo tanto, los tres vectores tienen componentes:

$${\ displaystyle \ mathbf {OA} = {\ begin {pmatrix} 0 \\ 0 \\ 1 \ end {pmatrix}}, \ quad \ mathbf {OB} = {\ begin {pmatrix} \ sin c \\ 0 \ \\ cos c \ end {pmatrix}}, \ quad \ mathbf {OC} = {\ begin {pmatrix} \ sin b \ cos A \\\ sin b \ sin A \\\ cos b \ end {pmatrix}} .}

El producto triple escalar , OA · ( OB × OC ) es el volumen del paralelepípedo formado por los vectores de posición de los vértices del triángulo esférico OA , OB y OC . Este volumen es invariante al sistema de coordenadas específico utilizado para representar OA , OB y OC . El valor del producto triple escalar OA · ( OB × OC ) es el determinante 3 × 3 con OA , OB y OCcomo sus filas. Con el eje Z a lo largo de OA,el cuadrado de este determinante es

{\ displaystyle {\ begin {alineado} {\ bigl (} \ mathbf {OA} \ cdot (\ mathbf {OB} \ times \ mathbf {OC}) {\ bigr)} ^ {2} & = {\ bigl ( } \ det (\ mathbf {OA}, \ mathbf {OB}, \ mathbf {OC}) {\ bigr)} ^ {2} \\ [4pt] & = \ left ({\ begin {vmatrix} 0 & 0 & 1 \\ \ sin c & 0 & \ cos c \\\ sin b \ cos A & \ sin b \ sin A & \ cos b \ end {vmatrix}} \ right) ^ {2} = \ left (\ sin b \ sin c \ sin A \ derecha) ^ {2}. \ end {alineado}}}

La repetición de este cálculo con el eje z a lo largo del OB da (sen c sin a sen B ) ² , mientras que con el z- eje a lo largo de OC es (sen a sen b sen C ) ² . Al igualar estas expresiones y dividirlas por (sin a sin b b sin c ) ²da

$${\ displaystyle {\ frac {\ sin ^ {2} A} {\ sin ^ {2} a}} = {\ frac {\ sin ^ {2} B} {\ sin ^ {2} b}} = { \ frac {\ sin ^ {2} C} {\ sin ^ {2} c}} = {\ frac {V ^ {2}} {\ sin ^ {2} a \ sin ^ {2} b \ sin ^ {2} c}},}

donde V es el volumen del paralelepípedo formado por el vector de posición de los vértices del triángulo esférico.

Es fácil ver cómo para los triángulos esféricos pequeños, cuando el radio de la esfera es mucho mayor que los lados del triángulo, esta fórmula se convierte en la fórmula plana en el límite, ya que

$${\ displaystyle \ lim _ {\ alpha \ rightarrow 0} {\ frac {\ sin \ alpha} {\ alpha}} = 1}

y lo mismo para el pecado β y el pecado γ .

Prueba geométrica [ editar ]

Considere un círculo unitario con:

$${\ displaystyle OA = OB = OC = 1}

Punto de construcción $${\ displaystyle D}y punto $${\ displaystyle E}tal que $${\ displaystyle \ angle ADO = \ angle AEO = 90 ^ {\ circ}}

Punto de construcción $${\ displaystyle A '}tal que $${\ displaystyle \ angle A'DO = \ angle A'EO = 90 ^ {\ circ}}

Por lo tanto, se puede ver que $${\ displaystyle \ angle ADA '= B}y $${\ displaystyle \ angle AEA '= C}

Darse cuenta de $${\ displaystyle A '}es la proyección de $${\ displaystyle A}en el avión $${\ displaystyle OBC}. Por lo tanto$${\ displaystyle \ angle AA'D = \ angle AA'E = 90 ^ {\ circ}}

Por trigonometría básica, tenemos:

$${\ displaystyle AD = \ sin c}

$${\ displaystyle AE = \ sin b}

Pero $${\ displaystyle AA '= AD \ sin B = AE \ sin C}

Combinándolos tenemos:

$${\ displaystyle \ sin c \ sin B = \ sin b \ sin C}

$${\ displaystyle {\ frac {\ sin B} {\ sin b}} = {\ frac {\ sin C} {\ sin c}}}

Aplicando un razonamiento similar, obtenemos la ley esférica del seno:

$${\ displaystyle {\ frac {\ sin A} {\ sin a}} = {\ frac {\ sin B} {\ sin b}} = {\ frac {\ sin C} {\ sin c}}}

Ver también: trigonometría esférica , ley esférica de los cosenos y fórmula de medio lado.

Caso hiperbólico [ editar ]

En la geometría hiperbólica, cuando la curvatura es −1, la ley de los senos se convierte en

$${\ displaystyle {\ frac {\ sin A} {\ sinh a}} = {\ frac {\ sin B} {\ sinh b}} = {\ frac {\ sin C} {\ sinh c}} \ ,. }

En el caso especial cuando B es un ángulo recto, uno obtiene

$${\ displaystyle \ sin C = {\ frac {\ sinh c} {\ sinh b}}}

que es el análogo de la fórmula en geometría euclidiana que expresa el seno de un ángulo como el lado opuesto dividido por la hipotenusa.

Véase también triángulo hiperbólico .

Formulación Unified [ editar ]

Defina una función sinusoidal generalizada, dependiendo también de un parámetro real K :

$${\ displaystyle \ sin _ {K} x = x - {\ frac {Kx ^ {3}} {3!}} + {\ frac {K ^ {2} x ^ {5}} {5!}} - {\ frac {K ^ {3} x ^ {7}} {7!}} + \ cdots.}

La ley de los senos en constante curvatura K se lee como ^[1]

$${\ displaystyle {\ frac {\ sin A} {\ sin _ {K} a}} = {\ frac {\ sin B} {\ sin _ {K} b}} = {\ frac {\ sin C} { \ sin _ {K} c}} \ ,.}

Al sustituir K = 0 , K = 1 y K = −1 , se obtienen respectivamente los casos euclidianos, esféricos e hiperbólicos de la ley de los senos descritos anteriormente.

Let p _K ( r ) indica la circunferencia de un círculo de radio r en un espacio de curvatura constante K . Entonces p _K ( r ) = 2π sin _K r . Por lo tanto, la ley de los senos también se puede expresar como:

$${\ displaystyle {\ frac {\ sin A} {p_ {K} (a)}} = {\ frac {\ sin B} {p_ {K} (b)}} = {\ frac {\ sin C} { p_ {K} (c)}} \ ,.}

Esta formulación fue descubierta por János Bolyai . ^[6]

Dimensiones superiores [ editar ]

Para un simplex n- dimensional (es decir, triángulo ( n = 2 ), tetraedro ( n = 3 ), pentatope ( n = 4 ), etc.) en el espacio euclidiano n- dimensional , el valor absoluto del seno polar de la normal Los vectores de las caras que se encuentran en un vértice , divididos por la hiperarea de la cara opuesta al vértice, son independientes de la elección del vértice. Escribiendo V para el hipervolumen de la nsimplex tridimensional y P para el producto de las hiperareas de sus ( n- 1) caras tridimensionales, la proporción común es

$${\ displaystyle {\ frac {(nV) ^ {n-1}} {(n-1)! P}}.}

Por ejemplo, un tetraedro tiene cuatro caras triangulares. El valor absoluto del seno polar de los vectores normales a las tres caras que comparten un vértice, dividido por el área de la cuarta cara, no dependerá de la elección del vértice:

{\ displaystyle {\ begin {alineado} & {\ frac {{\ bigl |} \ operatorname {psin} (\ mathbf {n_ {2}}, \ mathbf {n_ {3}}, \ mathbf {n_ {4} }) {\ bigr |}} {\ mathrm {Área} _ {1}}} = {\ frac {{\ bigl |} \ operatorname {psin} (\ mathbf {n_ {1}}, \ mathbf {n_ { 3}}, \ mathbf {n_ {4}}) {\ bigr |}} {\ mathrm {Área} _ {2}}} = {\ frac {{\ bigl |} \ operatorname {psin} (\ mathbf { n_ {1}}, \ mathbf {n_ {2}}, \ mathbf {n_ {4}}) {\ bigr |}} {\ mathrm {Área} _ {3}}} = {\ frac {{\ bigl |} \ operatorname {psin} (\ mathbf {n_ {1}}, \ mathbf {n_ {2}}, \ mathbf {n_ {3}}) {\ bigr |}} {\ mathrm {Área} _ {4 }}} \\ [4pt] = {} & {\ frac {(3 \ operatorname {Volume} _ {\ mathrm {tetrahedron}}) ^ {2}} {2! ~ \ Mathrm {Area} _ {1} \ mathrm {Area} _ {2} \ mathrm {Area} _ {3} \ mathrm {Area} _ {4}}} \,. \ end {alineado}}}

Historia [ editar ]

Según Ubiratàn D'Ambrosio y Helaine Selin , la ley esférica de los senos se descubrió en el siglo X. Se atribuye de diversas maneras a Abu-Mahmud Khojandi , Abu al-Wafa 'Buzjani , Nasir al-Din al-Tusi y Abu Nasr Mansur . ^[7]

Ibn Mu'adh al-Jayyani 's El libro de arcos desconocidos de una esfera en el siglo 11 contiene la ley general de senos. ^[8] La ley plana de los senos fue declarada más tarde en el siglo XIII por Nasīr al-Dīn al-Tūsī . En su En la figura del sector , declaró la ley de los senos para los triángulos esféricos y planos, y proporcionó pruebas de esta ley. ^[9]

Según Glen Van Brummelen , "La Ley de Sines es realmente la base de Regiomontanus para sus soluciones de triángulos rectángulos en el Libro IV, y estas soluciones son a su vez las bases para sus soluciones de triángulos generales". ^[10] Regiomontanus fue un matemático alemán del siglo XV.