TRIGONOMETRÍA

 ley de las tangentes ^[1] es una declaración acerca de la relación entre las tangentes de dos ángulos de un triángulo y las longitudes de los lados opuestos.

En la Figura 1, a , b y c son las longitudes de los tres lados del triángulo, y α, β y γ son los ángulos opuestos a esos tres lados respectivos. La ley de las tangentes establece que

$${\ displaystyle {\ frac {ab} {a + b}} = {\ frac {\ tan \ left ({\ tfrac {1} {2}} (\ alpha - \ beta) \ right)} {\ tan \ izquierda ({\ tfrac {1} {2}} (\ alpha + \ beta) \ right)}}.

La ley de las tangentes, aunque no es tan comúnmente conocida como la ley de los senos o la ley de los cosenos , es equivalente a la ley de los senos, y puede usarse en cualquier caso donde dos lados y el ángulo incluido, o dos ángulos y un lado , son conocidos.

Figura 1 - Un triángulo. Los ángulos α , β y γ son respectivamente opuestos a los lados a , b y c .

Prueba [ editar ]

Para probar la ley de las tangentes podemos comenzar con la ley de los senos :

$${\ displaystyle {\ frac {a} {\ sin \ alpha}} = {\ frac {b} {\ sin \ beta}}.

Dejar

$${\ displaystyle d = {\ frac {a} {\ sin \ alpha}} \ quad {\ text {y}} \ quad d = {\ frac {b} {\ sin \ beta}}}

así que eso

$${\ displaystyle a = d \ sin \ alpha \ quad {\ text {y}} \ quad b = d \ sin \ beta.}

Resulta que

$${\ displaystyle {\ frac {ab} {a + b}} = {\ frac {d \ sin \ alpha -d \ sin \ beta} {d \ sin \ alpha + d \ sin \ beta}} = {\ frac {\ sin \ alpha - \ sin \ beta} {\ sin \ alpha + \ sin \ beta}}.

Usando la identidad trigonométrica , la fórmula factorial para senos específicamente

$${\ displaystyle \ sin (\ alpha) \ pm \ sin (\ beta) = 2 \ sin \ left ({\ frac {\ alpha \ pm \ beta} {2}} \ right) \ cos \ left ({\ frac {\ alpha \ mp \ beta} {2}} \ derecha),}

obtenemos

$${\ displaystyle {\ frac {ab} {a + b}} = {\ frac {2 \ sin {\ tfrac {1} {2}} \ left (\ alpha - \ beta \ right) \ cos {\ tfrac { 1} {2}} \ left (\ alpha + \ beta \ right)} {2 \ sin {\ tfrac {1} {2}} \ left (\ alpha + \ beta \ right) \ cos {\ tfrac {1 } {2}} \ left (\ alpha - \ beta \ right)}} = {\ frac {\ sin {\ tfrac {1} {2}} \ left (\ alpha - \ beta \ right)} {\ cos {\ tfrac {1} {2}} \ left (\ alpha - \ beta \ right)}} \ div {\ frac {\ sin {\ tfrac {1} {2}} \ left (\ alpha + \ beta \ derecha)} {\ cos {\ tfrac {1} {2}} \ left (\ alpha + \ beta \ right)}} = {\ frac {\ tan \ left ({\ tfrac {1} {2}} ( \ alpha - \ beta) \ right)} {\ tan \ left ({\ tfrac {1} {2}} (\ alpha + \ beta) \ right)}}.}

Como alternativa al uso de la identidad para la suma o diferencia de dos senos, uno puede citar la identidad trigonométrica

$${\ displaystyle \ tan \ left ({\ frac {\ alpha \ pm \ beta} {2}} \ right) = {\ frac {\ sin \ alpha \ pm \ sin \ beta} {\ cos \ alpha + \ cos \ beta}}}

(Ver fórmula de medio ángulo tangente ).

Aplicación [ editar ]

La ley de las tangentes se puede usar para calcular el lado que falta y los ángulos de un triángulo en el que se dan dos lados a y b y el ángulo γ cerrado . Desde

$${\ displaystyle \ tan \ left ({\ tfrac {1} {2}} (\ alpha - \ beta) \ right) = {\ frac {ab} {a + b}} \ tan \ left ({\ tfrac { 1} {2}} (\ alpha + \ beta) \ right) = {\ frac {ab} {a + b}} \ cot \ left ({\ frac {\ gamma} {2}} \ right)}

uno puede calcular α - β ; junto con α + β = 180 ° - γ, esto produce α y β ; el lado c restante se puede calcular usando la ley de los senos . En el tiempo antes de que estuvieran disponibles las calculadoras electrónicas, este método era preferible a una aplicación de la ley de cosenos c = √ a ² + b ² - 2 ab cos γ , ya que esta última ley requería una búsqueda adicional en una tabla logarítmica, para calcular la raíz cuadrada. En los tiempos modernos, la ley de las tangentes puede tener mejores propiedades numéricas que la ley de los cosenos: si γ es pequeña, y a y b son casi iguales, entonces una aplicación de la ley de los cosenos conduce a una resta de valores casi iguales, lo que implica Una pérdida de dígitos significativos .

Versión esférica [ editar ]

En una esfera de radio unitario, los lados del triángulo son arcos de grandes círculos . Por consiguiente, sus longitudes pueden expresarse en radianes o en cualquier otra unidad de medida angular. Sean A , B , C los ángulos en los tres vértices del triángulo y sean a , b , c las longitudes respectivas de los lados opuestos. La ley esférica de las tangentes dice ^[2]

$${\ displaystyle {\ frac {\ tan \ left ({\ dfrac {AB} {2}} \ right)} {\ tan \ left ({\ dfrac {A + B} {2}} \ right)}} = {\ frac {\ tan \ left ({\ dfrac {ab} {2}} \ right)} {\ tan \ left ({\ dfrac {a + b} {2}} \ right)}}.}

Historia [ editar ]

La ley de tangentes para triángulos esféricos fue descrita en el siglo XIII por el matemático persa Nasir al-Din al-Tusi (1201–1274), quien también presentó la ley de los senos para triángulos de avión en su Tratado sobre el cuadrilátero de cinco volúmenes .

esfera Lénártida es un modelo de investigación docente y educativa para la geometría esférica . La esfera Lénártida es una sustitución moderna de una "pizarra esférica". ^[1] [2] Se puede usar para visualizar polígonos esféricos (especialmente triángulos ) que muestran las relaciones entre los lados y los ángulos .

Conjunto básico [ editar ]

El set básico de Lenart Sphere incluye: ^[3]

• Un plástico transparente, esfera de ocho pulgadas.
• Un soporte en forma de anillo, llamado toro , para colocar debajo de la esfera.
• Transparencias hemisféricas que se ajustan sobre la esfera para que los estudiantes puedan dibujarlas con marcadores de colores y recortar formas con tijeras.
• Una regla esférica con dos bordes a escala para dibujar y medir arcos, ángulos y grandes círculos en la esfera
• Un compás esférico y un localizador central para dibujar círculos en la esfera.
• Un conjunto de marcadores de transparencia para escribir y dibujar en la esfera y transparencias.
• Un colgador para mostrar tus construcciones esféricas y diseños.
• Un folleto de 16 páginas, "Cómo comenzar en la esfera de Lenart", con actividades que se pueden comenzar en cuanto se abre el cuadro.
• Una proyección policónica de la Tierra en cuatro colores que se puede cortar y transformar en un globo.

Productos relacionados [ editar ]

Triángulo equilátero construido sobre una esfera de lenart.

Otros productos para estudiar geometría esférica incluyen programas de software de visualización como el Geometer's Sketchpad , GeoGebra y Spherical Easel ^[4] (consulte los enlaces externos para obtener información sobre la Esfera esférica y visite la Lista de software de geometría interactiva para no Euclides y muchas otras geometríasinteractivas proyectivas aplicaciones y programas). Donde estos productos solo funcionan en un plano , la esfera Lénárt está brindando experiencia práctica de geometría esférica.

Historia [ editar ]

Ver también: Historia de la trigonometría.

La esfera Lénárt fue inventada por István Lénárt en Hungría a principios de la década de 1990 y su uso se describe en su libro de 2003 comparando la geometría plana y la esférica. ^[5]

La trigonometría esférica solía ser un tema matemático importante desde la antigüedad hasta el final de la Segunda Guerra Mundial , y ha sido reemplazada en la educación moderna y (en navegación) con más métodos algorítmicos y GPS , incluida la fórmula de Haversine , multiplicación de matrices algebraicas lineales , y el pentágono de Napier . La esfera Lénárt todavía se utiliza ampliamente en toda Europa en geometría no euclidiana , así como en cursos de SIG .

Teselación esférica [ editar ]

La esfera Lénárt es útil para modelar y demostrar técnicas de teselación esférica, especialmente cuando se aplican a problemas de análisis finitos. Usando programas de gráficos 3D o código Python (consulte el enlace de referencia externa 8 para ver ejemplos de código de código abierto de Python vs. NURBS ), se pueden proyectar un mayor número de polígonos hacia y desde la esfera tanto para el análisis de elementos finitos como para la síntesis de objetos y características en la esfera, como el planeta montado en asteroides en el ejemplo. En este caso, la esfera Lénárt es útil para la teselación (tiling) como un atajo de simplificación o aproximación a la matemática diferencial extremadamente compleja del análisis finito y la construcción (técnicamente: modelado), especialmente de objetos animados.

curva de Lissajous / l ɪ s ə ʒ U / , también conocido como figura de Lissajous o curva de Bowditch / b aʊ d ɪ tʃ / , es la gráfica de un sistema de ecuaciones paramétricas

$${\ displaystyle x = A \ sin (en + \ delta), \ quad y = B \ sin (bt),}

que describen el movimiento armónico complejo . Esta familia de curvasfue investigada por Nathaniel Bowditch en 1815, y luego en más detalle por Jules Antoine Lissajous en 1857.

La apariencia de la figura es altamente sensible a la relación a/b . Para una relación de 1, la figura es una elipse , con casos especiales que incluyen círculos ( A = B , δ = π/2 radianes ) y líneas ( δ = 0 ). Otra figura simple de Lissajous es la parábola ( b/a = 2 , δ = π/4 ). Otras relaciones producen curvas más complicadas, que se cierran solo si a/b esracional. La forma visual de estas curvas a menudo sugiere unnudotridimensional, y de hecho, muchos tipos de nudos, incluidos los conocidos comonudos de Lissajous, se proyectan al plano como figuras de Lissajous.

Visualmente, la relación a/b determina el número de "lóbulos" de la figura. Por ejemplo, una proporción de 3/1 o 1/3produce una figura con tres lóbulos principales (ver imagen). Del mismo modo, una relación de 5/4 produce una figura con cinco lóbulos horizontales y cuatro lóbulos verticales. Las proporciones racionales producen cifras cerradas (conectadas) o "fijas", mientras que las proporciones irracionales producen cifras que parecen rotar. La relación A/B determina la relación de ancho a altura relativa de la curva. Por ejemplo, una proporción de 2/1produce una figura que es dos veces más ancha que alta. Finalmente, el valor de δ determina el ángulo de "rotación" aparente de la figura, visto como si fuera realmente una curva tridimensional. Por ejemplo, δ = 0 produce componentes x e y que están exactamente en fase, por lo que la figura resultante aparece como una figura tridimensional aparente vista de frente (0 °). Por el contrario, cualquier δ que no sea cero produce una figura que parece ser girada, ya sea como una rotación de izquierda a derecha o de arriba hacia abajo (según la relación a/b).

Figura de Lissajous en un osciloscopio , que muestra una relación 1: 3 entre las frecuencias de las entradas sinusoidales vertical y horizontal, respectivamente.

Figuras de Lissajous donde a = 1 , b = N ( N es un número natural ) y

$${\ displaystyle \ delta = {\ frac {N-1} {N}} {\ frac {\ pi} {2}}}

son polinomios de Chebyshev de la primera clase de grado N . Esta propiedad se explota para producir un conjunto de puntos, llamados puntos Padua , en los que se puede muestrear una función para calcular una interpolación bivariada o una cuadratura de la función sobre el dominio [−1,1] × [−1,1 ] .

La relación de algunas curvas de Lissajous con los polinomios de Chebyshev es más clara de entender si la curva de Lissajous que genera cada una de ellas se expresa mediante funciones de coseno en lugar de funciones sinusoidales.

$${\ displaystyle x = \ cos (t), \ quad y = \ cos (Nt)}

Ejemplos [ editar ]

Animación que muestra la adaptación de curvas a medida que la relación a/b aumenta de 0 a 1

La animación muestra la adaptación curva con el aumento de forma continua un/b fracción de 0 a 1 en pasos de 0,01 ( δ = 0).

A continuación se muestran ejemplos de figuras de Lissajous con δ = π/2 , un número natural impar a , un número naturalpar b , y | a - b | = 1 .

• 

  a = 1 , b = 2 (1: 2)
 
• 

  a = 3 , b = 2 (3: 2)
• 

  a = 3 , b = 4 (3: 4)
 
• 

  a = 5 , b = 4 (5: 4)

Generación [ editar ]

Antes de los equipos electrónicos modernos, las curvas de Lissajous se podían generar mecánicamente por medio de un armonógrafo .

Aplicación práctica [ editar ]

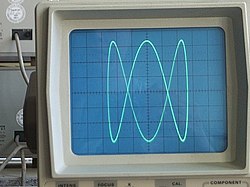
Las curvas de Lissajous también se pueden generar usando un osciloscopio (como se ilustra). Se puede usar un circuito de pulpo para demostrar las imágenes de forma de onda en un osciloscopio. Se aplican dos entradas sinusoidales de desplazamiento de fase al osciloscopio en modo XY y la relación de fase entre las señales se presenta como una figura de Lissajous.

En el mundo del audio profesional, este método se utiliza para el análisis en tiempo real de la relación de fase entre los canales izquierdo y derecho de una señal de audio estéreo. En las consolas de mezcla de audio más grandes y sofisticadas, se puede incorporar un osciloscopio para este propósito.

En un osciloscopio, suponemos que x es CH1 e y es CH2, A es la amplitud de CH1 y B es la amplitud de CH2, aes la frecuencia de CH1 yb es la frecuencia de CH2, por lo que a/b es la relación de frecuencias de los dos canales, y δ es el desplazamiento de fase de CH1.

Una aplicación puramente mecánica de una curva de Lissajous con a = 1 , b = 2 se encuentra en el mecanismo de conducción del tipo de Luz de Marte de las lámparas de haz oscilante populares en los ferrocarriles a mediados del siglo XX. La viga en algunas versiones traza un patrón de figura 8 ladeado en su lado.

Solicitud para el caso de a = b [ editar ]

En esta figura, ambas frecuencias de entrada son idénticas, pero la variación de fase entre ellas crea la forma de una elipse .

Arriba: Señal de salida en función del tiempo. 
Medio: señal de entrada en función del tiempo. 
Abajo: la curva de Lissajous resultante cuando la salida se traza como una función de la entrada. 
En este ejemplo particular, debido a que la salida está desfasada 90 grados de la entrada, la curva de Lissajous es un círculo y gira en sentido contrario a las agujas del reloj.

Cuando la entrada a un sistema LTI es sinusoidal, la salida es sinusoidal con la misma frecuencia, pero puede tener una amplitud diferente y algún cambio de fase . El uso de un osciloscopio que puede trazar una señal contra otra (en lugar de una señal contra el tiempo) para trazar la salida de un sistema LTI contra la entrada al sistema LTI produce una elipse que es una figura de Lissajous para el caso especial de a = b . La relación de aspecto de la elipse resultante es una función del cambio de fase entre la entrada y la salida, con una relación de aspecto de 1 (círculo perfecto) correspondiente a un desplazamiento de fase de ± 90 ° y una relación de aspecto de ∞ (una línea) correspondiente a un cambio de fase de 0 ° o 180 °.^[1]

La siguiente figura resume cómo cambia la figura de Lissajous en diferentes cambios de fase. Los cambios de fase son todos negativos, por lo que la semántica de retardo se puede usar con un sistema LTI causal (tenga en cuenta que −270 ° es equivalente a + 90 °). Las flechas muestran la dirección de rotación de la figura de Lissajous. ^[1]

Un cambio de fase puro afecta la excentricidad del óvalo de Lissajous. El análisis del óvalo permite medir el cambio de fase de un sistema LTI .

En ingenieria [ editar ]

Una curva de Lissajous se usa en pruebas experimentales para determinar si un dispositivo se puede clasificar correctamente como un memristor . ^{[ cita requerida ]}

En la cultura [ editar ]

En la película [ editar ]

Animación lissajous estilo ciencia ficción.

Las figuras de Lissajous a veces se mostraban en osciloscopios diseñados para simular equipos de alta tecnología en programas de televisión y películas de ciencia ficción en los años sesenta y setenta. ^[2]

La secuencia del título de John Whitney para la película Vertigo de Alfred Hitchcock de 1958 se basa en figuras de Lissajous. ^[3]

En una secuencia hacia el final de un episodio de Columbo titulado "Hazme un asesinato perfecto", el detective se sienta mirando las curvas de Lissajous que se muestran con la música en los monitores de una televisión fuera de la camioneta.

Logotipos de la empresa [ editar ]

Las figuras de Lissajous se utilizan a veces en diseño gráfico como logotipos . Ejemplos incluyen:

• The Australian Broadcasting Corporation ( a = 1 , b = 3 , δ = π/2 ) ^[4]
• El Laboratorio Lincoln en MIT ( a = 4 , b = 3 , δ = 0 ) ^[5]
• La Universidad de Electro-Comunicaciones , Japón ( a = 5 , b = 6 , δ = π/2 ). ^{[ cita requerida ]}
• La aplicación de video streaming de Disney's Movies Anywhere utiliza una versión estilizada de la curva

En el arte moderno [ editar ]

Más información: Matemáticas y arte.

• El artista dadaísta Max Ernst pintó figuras de Lissajous directamente al balancear un cubo de pintura pinchado sobre un lienzo.