MATEMÁTICAS ELEMENTALES

ÁLGEBRA ELEMENTAL - FRACCIONES

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Racionales diádicos en el intervalo de 0 a 1.

En matemáticas , una fracción diádica o racional diádicoes un número racional cuyo denominador , cuando la relación está en términos mínimos (coprime), es un poder de dos , es decir, un número de la forma$${\ displaystyle {\ frac {a} {2 ^ {b}}}}donde a es un número entero y b es un número natural ; por ejemplo, 1/2 o 3/8, pero no 1/3. Estos son precisamente los números que poseen una expansión binaria finita .

Uso en medida [ editar ]

La pulgada se subdivide habitualmente en fracciones diádicas en lugar de decimales; de manera similar, las divisiones habituales del galón en medio galón, cuarto de galón y pintas son diádicas. Los antiguos egipcios también utilizaron fracciones diádicas en la medida, con denominadores de hasta 64. ^[1]

Aritmética [ editar ]

La suma , el producto o la diferencia de dos fracciones diádicas es otra fracción diádica:

$${\ displaystyle {\ frac {a} {2 ^ {b}}} + {\ frac {c} {2 ^ {d}}} = {\ frac {2 ^ {db} a + c} {2 ^ { d}}} \ quad (d \ geq b)}

$${\ displaystyle {\ frac {a} {2 ^ {b}}} - {\ frac {c} {2 ^ {d}}} = {\ frac {2 ^ {db} ac} {2 ^ {d} }} \ quad (d \ geq b)}

{\ displaystyle {\ frac {a} {2 ^ {b}}} - {\ frac {c} {2 ^ {d}}} = {\ frac {a-2 ^ {bd} c} {2 ^ { b}}} \ quad (d

$${\ displaystyle {\ frac {a} {2 ^ {b}}} \ times {\ frac {c} {2 ^ {d}}} = {\ frac {a \ times c} {2 ^ {b + d }}}.}

Sin embargo, el resultado de dividir una fracción diádica por otra no es necesariamente una fracción diádica.

La adición módulo 1 forma un grupo; Este es el Prüfer 2-group .

Propiedades adicionales [ editar ]

Debido a que están cerradas bajo la adición, sustracción y multiplicación, pero no división, las fracciones diádicas forman un subanillo de los números racionales Q y un overring de los enteros Z . Algebraicamente, esta subring es la localización de los enteros Z con respecto al conjunto de potencias de dos.

El conjunto de todas las fracciones diádicas es denso en la línea real : cualquier número real x puede aproximarse arbitrariamente de forma aproximada por los racionales diádicos de la forma$${\ displaystyle \ lfloor 2 ^ {i} x \ rfloor / 2 ^ {i}}. En comparación con otros subgrupos densos de la línea real, como los números racionales, los racionales diádicos son, en cierto sentido, un conjunto denso relativamente "pequeño", por lo que a veces aparecen como pruebas. (Véase por ejemplo el lema de Urysohn .)

Si bien es cierto que las fracciones diádicas son precisamente aquellos números que poseen expansiones binarias finitas, sus expansiones binarias no son únicas; hay una representación finita y una representación infinita de cada una, con exactamente dos representaciones binarias infinitas para cada una distinta de 0. Por ejemplo, 0.1000… ₂  = 0.0111… ₂  = 1/4 + 1/8 + 1/16 +… = 1/2. Además, 0.11000… ₂  = 0.10111… ₂  = 3/4. Sería más preciso decir que estos números tienen representaciones binarias que eventualmente son constantes.

Grupo dual [ editar ]

Considerando solo las operaciones de suma y resta de los racionales diádicos les da la estructura de un grupo abeliano aditivo . El grupo dual de un grupo consiste en sus caracteres , grupo homomorfismos al grupo multiplicativo de los números complejos , y en el espíritu de la dualidad de Pontryagin, el grupo dual de los racionales diádicos aditivos también se puede ver como un grupo topológico . Se llama solenoide diádico y es un ejemplo de un grupo solenoide y de un protoro .

Los racionales diádicos son el límite directo de los subgrupos cíclicos infinitos de los números racionales,

$${\ displaystyle \ varinjlim \ left \ {2 ^ {- i} \ mathbb {Z} \ mid i = 0,1,2, \ dots \ right \}}

y su grupo dual se puede construir como el límite inverso del grupo de círculo unitario bajo el mapa de cuadratura repetida

$${\ displaystyle \ zeta \ mapsto \ zeta ^ {2}.}

Un elemento del solenoide diádico puede representarse como una secuencia infinita de números complejos q ₀ , q ₁ , q ₂ , ..., con las propiedades de que cada q _{i se} encuentra en el círculo unitario y que, para todos i  > 0, q _i ² =  q _{i - 1} . La operación de grupo en estos elementos multiplica cualquiera de las dos secuencias por componentes. Cada elemento del solenoide diádico corresponde a un carácter de los racionales diádicos que mapea a / 2 ^b al número complejo q _b ^a . Por el contrario, todos los personajes χde los racionales diádicos corresponde al elemento del solenoide diádico dado por q _i  =  χ (1/2 ⁱ ).

Como espacio topológico, el solenoide diádico es un solenoide , y un continuo indecomposible . ^[2]

Construcciones relacionadas [ editar ]

Los números surrealistas son generados por un principio de construcción iterado que comienza generando todas las fracciones diádicas finitas, y luego continúa creando tipos nuevos y extraños de números infinitos, infinitesimales y otros.

La secuencia binaria de van der Corput es una permutación equidistribuida de los números racionales diádicos positivos.

En la música [ editar ]

Las firmas de tiempo en la notación musical occidental tradicionalmente consisten en fracciones diádicas (por ejemplo: 2/2, 4/4, 6/8 ...), aunque los compositores han introducido firmas de tiempo no diádicas en el siglo veinte (por ejemplo: 2 / . , lo que literalmente significa 2/ ³ / ₈ ). Las firmas de tiempo no diádicas se llaman irracionalesen la terminología musical, pero este uso no corresponde a los números irracionales de las matemáticas, porque aún consisten en proporciones de enteros. Las firmas de tiempo irracional en el sentido matemático son muy raras, pero un ejemplo ( √ 42/1 ) aparece en Conlon Nancarrow's Estudios para piano de jugador .

En informática [ editar ]

Como un tipo de datos utilizado por las computadoras, los números de punto flotante a menudo se definen como enteros multiplicados por potencias positivas o negativas de dos, y por lo tanto, todos los números que pueden representarse, por ejemplo, por tipos de datos binarios de punto flotante IEEE son racionales diádicos. Lo mismo es cierto para la mayoría de los tipos de datos de punto fijo , que también usan poderes de dos implícitamente en la mayoría de los casos.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Diagrama de Farey a F ₉ representado con arcos circulares. En la imagen SVG , desplácese sobre una curva para resaltarla y sus términos.

Diagrama de Farey a F ₉ .

Patrón simétrico realizado por los denominadores de la secuencia de Farey, F ₉ .

Patrón simétrico realizado por los denominadores de la secuencia de Farey, F ₂₅ .

En matemáticas , la secuencia de Farey de orden n es la secuencia de fracciones completamente reducidas , ya sea entre 0 y 1, o sin esta restricción, ^[1] que cuando está en los términos más bajos tiene denominadores menores o iguales a n , dispuestas en orden de aumento tamaño.

Con la definición restringida, cada secuencia de Farey comienza con el valor 0, indicado por la fracción ⁰ ⁄ ₁ , y termina con el valor 1, indicado por la fracción ¹ ⁄ ₁ (aunque algunos autores omiten estos términos).

Una secuencia de Farey a veces se denomina serie deFarey , ^{[ cita requerida ]} que no es estrictamente correcta, porque los términos no están sumados.

Ejemplos [ editar ]

Las secuencias de Farey de las órdenes 1 a 8 son:

F ₁ = { 0/1 _, 1/1 }

F ₂ = { 0/1 _, 1/2 _, 1/1 }

F ₃ = { 0/1 _, 1/3 _, 1/2 _, 2/3 _, 1/1 }

F ₄ = { 0/1 _, 1/4 _, 1/3 _, 1/2 _, 2/3 _, 3/4 _, 1/1 }

F ₅ = { 0/1 _, 1/5 _, 1/4 _, 1/3 _, 2/5 _, 1/2 _, 3/5 _, 2/3 _, 3/4 _, 4/5 _, 1/1 }

F ₆ = { 0/1 _, 1/6 _, 1/5 _, 1/4 _, 1/3 _, 2/5 _, 1/2 _, 3/5 _, 2/3 _, 3/4 _, 4/5 _, 5/6 _, 1/1 }

F ₇ = { 0/1 _, 1/7 _, 1/6 _, 1/5 _, 1/4 _, 2/7 _, 1/3 _, 2/5 _, 3/7 _, 1/2 _, 4/7 _, 3/5 _, 2/3 _, 5/7 _, 3/4 _, 4/5 _, 5/6 _, 6/7 _, 1/1 }

F ₈ = { 0/1 _, 1/8 _, 1/7 _, 1/6 _, 1/5 _, 1/4 _, 2/7 _, 1/3 _, 3/8 _, 2/5 _, 3/7 _, 1/2 _, 4/7 _, 3/5 _, 5/8 _, 2/3 _, 5/7 _, 3/4 _, 4/5 _, 5/6 _, 6/7 _, 7/8 _, 1/1 }

Centrado
F 1 = { 0/1 , 1/1 }
F 2 = { 0/1 , 1/2 , 1/1 }
F 3 = { 0/1 , 1/3 , 1/2 , 2/3 , 1/1 }
F 4 = { 0/1 , 1/4 , 1/3 , 1/2 , 2/3 , 3/4 , 1/1 }
F 5 = { 0/1 , 1/5 , 1/4 , 1/3 , 2/5 , 1/2 , 3/5 , 2/3 , 3/4 , 4/5 , 1/1 }
F 6 = { 0/1 , 1/6 , 1/5 , 1/4 , 1/3 , 2/5 , 1/2 , 3/5 , 2/3 , 3/4 , 4/5 , 5/6 , 1/1 }
F 7 = { 0/1 , 1/7 , 1/6 , 1/5 , 1/4 , 2/7 , 1/3 , 2/5 , 3/7 , 1/2 , 4/7 , 3/5 , 2/3 , 5/7 , 3/4 , 4/5 , 5/6 , 6/7 , 1/1 }
F 8 = { 0/1 , 1/8 , 1/7 , 1/6 , 1/5 , 1/4 , 2/7 , 1/3 , 3/8 , 2/5 , 3/7 , 1/2 , 4/7 , 3/5 , 5/8 , 2/3 , 5/7 , 3/4 , 4/5 , 5/6 , 6/7 , 7/8 , 1/1 }

Ordenados

F1 = {0/1, 1/1} F2 = {0/1, 1/2, 1/1} F3 = {0/1, 1/3, 1/2, 2/3, 1/1} F4 = {0/1, 1/4, 1/3, 1/2, 2/3, 3/4, 1/1} F5 = {0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1} F6 = {0/1, 1/6, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6 1/1} F7 = {0/1, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 2/5, 3/7, 1/2, 4/7, 3/5 , 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 1/1} F8 = {0/1, 1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2 , 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8, 1/1}

Historia [ editar ]

La historia de 'Farey series' es muy curiosa : Hardy y Wright (1979) Capítulo III ^[2]

... una vez más, el hombre cuyo nombre fue dado a una relación matemática no fue el descubridor original en lo que respecta a los registros. - Beiler (1964) Capítulo XVI ^[3]

Secuencias de Farey llevan el nombre de la British geólogo John Farey, padre , cuya carta sobre estas secuencias fue publicado en el Philosophical Magazine en 1816. Farey conjeturó, sin ofrecer pruebas, que cada nuevo término en una secuencia de expansión Farey es el mediant de sus vecinos . Cauchy leyó la carta de Farey , quien proporcionó una prueba en sus Exercices de mathématique y atribuyó este resultado a Farey. De hecho, otro matemático, Charles Haros , había publicado resultados similares en 1802 que Farey o Cauchy no conocían. ^[3]Así fue un accidente histórico que vinculó el nombre de Farey con estas secuencias. Este es un ejemplo de la ley de eponimia de Stigler .

Propiedades [ editar ]

Longitud de la secuencia e índice de una fracción [ editar ]

La secuencia Farey de orden n contiene todos los miembros de las secuencias Farey de órdenes inferiores. En particular, F _n contiene todos los miembros de F _n −1 y también contiene una fracción adicional para cada número que es menor que n y coprime a n . Por lo tanto F ₆ consta de F ₅ junto con las fracciones 1/6 y 5/6 .

El término medio de una secuencia de Farey F _n es siempre 1/2 , para n > 1. A partir de este, podemos relacionar las longitudes de F _n y F _n -1utilizando la función totient de Euler $${\ displaystyle \ varphi (n)} :

$${\ displaystyle | F_ {n} | = | F_ {n-1} | + \ varphi (n).}

Usando el hecho de que | F ₁ | = 2, podemos derivar una expresión para la longitud de F _n ^[4] :

$${\ displaystyle | F_ {n} | = 1 + \ sum _ {m = 1} ^ {n} \ varphi (m) = 1 + \ Phi (n),}

dónde $${\ displaystyle \ Phi (n)} es la sumatoria sumatoria.

También tenemos :

$${\ displaystyle | F_ {n} | = {\ frac {1} {2}} \ left (3+ \ sum _ {d = 1} ^ {n} \ mu (d) \ left \ lfloor {\ tfrac { n} {d}} \ right \ rfloor ^ {2} \ right),}

y por una fórmula de inversión de Möbius  :

$${\ displaystyle | F_ {n} | = {\ frac {1} {2}} (n + 3) n- \ sum _ {d = 2} ^ {n} | F _ {\ lfloor n / d \ rfloor} |

donde µ ( d ) es la función de Möbius de la teoría de números , y $${\ displaystyle \ lfloor {\ tfrac {n} {d}} \ rfloor}Es la función de piso .

El comportamiento asintótico de | F _n | es :

$${\ displaystyle | F_ {n} | \ sim {\ frac {3n ^ {2}} {\ pi ^ {2}}}.}

El índice $${\ displaystyle I_ {n} (a_ {k, n}) = k} de una fracción $${\ displaystyle a_ {k, n}} en la secuencia de Farey $${\ displaystyle F_ {n} = \ {a_ {k, n}: k = 0,1, \ ldots, m_ {n} \}} es simplemente la posición que $${\ displaystyle a_ {k, n}} ocupa en la secuencia. Esto es de especial relevancia ya que se utiliza en una formulación alternativa de la hipótesis de Riemann , ver más abajo . Varias propiedades útiles siguen:

$${\ displaystyle I_ {n} (0/1) = 0,}

$${\ displaystyle I_ {n} (1 / n) = 1,}

$${\ displaystyle I_ {n} (1/2) = (| F_ {n} | -1) / 2,}

$${\ displaystyle I_ {n} (1/1) = | F_ {n} | -1,}

$${\ displaystyle I_ {n} (h / k) = | F_ {n} | -1-I_ {n} ((kh) / k).}

El índice de $${\ displaystyle 1 / k} dónde {\ displaystyle n / (i + 1)  y $${\ displaystyle n}Es el mínimo común múltiplo de la primera.$${\ displaystyle i} números, $${\ displaystyle n = {\ rm {lcm}} ([2, i])}, viene dada por ^[5] :

$${\ displaystyle I_ {n} (1 / k) = 1 + n \ sum _ {j = 1} ^ {i} {\ frac {\ varphi (j)} {j}} - k \ Phi (i). }

Vecinos cariñosos [ editar ]

Las fracciones que son términos vecinos en cualquier secuencia de Farey se conocen como un par de Farey y tienen las siguientes propiedades.

Si a/b y c/d son vecinos en una secuencia de Farey, con a/b  <  c/d , entonces su diferencia c/d  -  a/b es igual a 1/bd . ^{[ ¿Por qué? ]} Desde

$${\ displaystyle {\ frac {c} {d}} - {\ frac {a} {b}} = {\ frac {bc-ad} {bd}},}

esto es equivalente a decir que

$${\ displaystyle bc-ad = 1}.

Por lo tanto 1/3 y 2/5 son vecinos en F ₅ , y su diferencia es 1/15 .

Lo contrario también es cierto. Si

$${\ displaystyle bc-ad = 1}

para enteros positivos a , b , c y d con a < b y c < d, entonces a/b y c/d serán vecinos en la secuencia de Farey de orden máximo ( b, d ).

Si p/q tiene vecinos a/b y c/d en alguna secuencia de Farey, con

{\ displaystyle {\ frac {a} {b}} <{\ frac {p} {q}} <{\ frac {c} {d}}}

entonces p/q es la media de a/b y c/d - en otras palabras,

$${\ displaystyle {\ frac {p} {q}} = {\ frac {a + c} {b + d}}.

Esto se desprende fácilmente de la propiedad anterior, ya que si bp - aq = qc - pd = 1 , entonces bp + pd = qc + aq , p ( b + d ) = q ( a + c ) , p/q = a + c/b + d .

De ello se deduce que si a/b y c/d son vecinos en una secuencia de Farey, entonces el primer término que aparece entre ellos a medida que se incrementa el orden de la secuencia de Farey es

$${\ displaystyle {\ frac {a + c} {b + d}}

que aparece por primera vez en la secuencia de Farey de orden b + d .

Así, el primer término que aparezca entre 1/3 y 2/5 es 3/8 , que aparece en F ₈ .

El árbol de Stern-Brocot es una estructura de datos que muestra cómo la secuencia se construye a partir de 0 (= 0/1 ) y 1 (= 1/1 ), mediante la adopción de mediants sucesivas.

Las fracciones que aparecen como vecinos en una secuencia de Farey tienen expansiones de fracciones continuas estrechamente relacionadas . Cada fracción tiene dos expansiones de fracción continua: en una, el término final es 1; en el otro, el término final es mayor que 1. Si p/q , que aparece por primera vez en la secuencia Farey F _q , tiene expansiones de fracciones continuas

[0; a ₁ , a ₂ , ..., a _{n - 1} , a _n , 1]

[0; a ₁ , a ₂ , ..., a _{n - 1} , a _n + 1]

entonces el vecino más cercano de p/q en F _q (que será su vecino con el denominador más grande) tiene una expansión de fracción continua

[0; a ₁ , a ₂ , ..., a _n ]

y su otro vecino tiene una expansión fraccionada continua.

[0; a ₁ , a ₂ , ..., a _{n - 1} ]

Por ejemplo, 3/8 tiene las dos expansiones fracción continua [0; 2, 1, 1, 1] y [0; 2, 1, 2] , y sus vecinos en F ₈ son 2/5, que se puede ampliar como [0; 2, 1, 1] ; y 1/3 , que se puede ampliar como [0; 2, 1] .

Farey fracciones y el mínimo común múltiplo [ editar ]

En ^[6] y ^[7] se muestra que el mcm se puede expresar como los productos de las fracciones de Farey como

{\ displaystyle lcm ([2, N]) = {\ frac {1} {2}} \ left (1+ \ prod _ {r \ en F_ {N}, 0

Farey fracciones y el mayor divisor común [ editar ]

Para cualquiera de las 3 fracciones de Farey a/b , c/d y e/f, la siguiente identidad entre los gcd 's de los determinantesde la matriz 2x2 en valor absoluto es válida para ^[8] :

{\ displaystyle \ gcd \ left ({\ begin {Vmatrix} a & c \\ b & d \ end {Vmatrix}}, {\ begin {Vmatrix} a & e \\ b & f \ end {Vmatrix}} \ right) = \ gcd \ left ( {\ begin {Vmatrix} a & c \\ b & d \ end {Vmatrix}}, {\ begin {Vmatrix} c & e \\ d & f \ end {Vmatrix}} \ right) = \ gcd \ left ({\ begin {Vmatrix} a & e \ b & f \ end {Vmatrix}}, {\ begin {Vmatrix} c & e \\ d & f \ end {Vmatrix}} \ right)}

Aplicaciones [ editar ]

Las secuencias de Farey son muy útiles para encontrar aproximaciones racionales de números irracionales. ^[9]Por ejemplo, la construcción por Eliahou ^[10] de un límite inferior en la duración de los ciclos no triviales en el proceso 3 x +1 usa secuencias de Farey para calcular una expansión de fracción continua del número log ₂ (3).

En sistemas físicos que presentan fenómenos de resonancia, las secuencias de Farey proporcionan un método muy elegante y eficiente para calcular las ubicaciones de resonancia en 1D ^[11] y 2D. ^[12]

Las secuencias de Farey son prominentes en los estudios de planificación de trayectorias de cualquier ángulo en cuadrículas de celdas cuadradas, por ejemplo en la caracterización de su complejidad computacional ^[13] u optimalidad ^[14] . La conexión se puede considerar en términos de rutas restringidas en r , es decir, rutas formadas por segmentos de línea que cada una atraviesa como máximo.$${\ displaystyle r} filas y como máximo $${\ displaystyle r} columnas de celdas. Dejar$${\ displaystyle Q} ser el conjunto de vectores $${\ displaystyle (q, p)} tal que $${\ displaystyle 1 \ leq q \ leq r}, $${\ displaystyle 0 \ leq p \ leq q}y $${\ displaystyle p}, $${\ displaystyle q}son coprimos. Dejar$${\ displaystyle Q *}ser el resultado de reflejar $${\ displaystyle Q} En la linea $${\ displaystyle y = x}. Dejar$${\ displaystyle S = \ {(\ pm x, \ pm y) :( x, y) \ en Q \ cup Q * \}}. Entonces, cualquier ruta restringida por r se puede describir como una secuencia de vectores de$${\ displaystyle S}. Tenga en cuenta que hay una bijección entre$${\ displaystyle Q} y la secuencia de orden de Farey $${\ displaystyle r} dada por $${\ displaystyle (q, p)} mapeo a $${\ displaystyle {\ tfrac {p} {q}}}.

Círculos de Ford [ editar ]

Comparación de los círculos de Ford y un diagrama de Farey con arcos circulares para n desde 1 hasta 9. Tenga en cuenta que cada arco interseca sus círculos correspondientes en ángulos rectos. En la imagen SVG , pase el cursor sobre un círculo o curva para resaltarlo y sus términos.

Hay una conexión entre la secuencia de Farey y los círculos de Ford.

Para cada fracción p / q (en sus términos más bajos) hay un círculo de Ford C [ p / q ], que es el círculo con el radio 1 / (2 q ² ) y el centro en ( p / q , 1 / (2 q ² )). Dos círculos de Ford para diferentes fracciones son disjuntos o son tangentes entre sí: dos círculos de Ford nunca se intersectan. Si 0 < p / q <1 a="" c="" de="" entonces="" font="" ford="" los="" nbsp="" que="" rculos="" son="" tangentes="">p / q ] son ​​precisamente los círculos de Ford para fracciones que son vecinos de p / q en alguna secuencia de Farey.

Así, C [2/5] es tangente a C [1/2], C [1/3], C [3/7], C [3/8] etc.

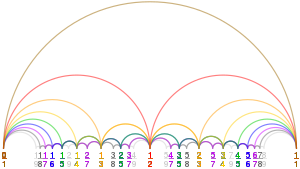
Los círculos de Ford aparecen también en la junta de Apollonian(0,0,1,1). La siguiente imagen ilustra esto junto con las líneas de resonancia de Farey.

Junta de Apollonian (0,0,1,1) y el diagrama de resonancia de Farey.

Hipótesis de Riemann [ editar ]

Las secuencias de Farey se utilizan en dos formulaciones equivalentes de la hipótesis de Riemann . Supongamos que los términos de$${\ displaystyle F_ {n}} son $${\ displaystyle \ {a_ {k, n}: k = 0,1, \ ldots, m_ {n} \}}. Definir$${\ displaystyle d_ {k, n} = a_ {k, n} -k / m_ {n}}, en otras palabras $${\ displaystyle d_ {k, n}}es la diferencia entre el k ésimo término de la n ª secuencia de Farey y el k ª miembro de un conjunto del mismo número de puntos, distribuidos uniformemente en el intervalo de la unidad. En 1924 Jérôme Franel ^[15] demostró que la declaración

{\ displaystyle \ sum _ {k = 1} ^ {m_ {n}} d_ {k, n} ^ {2} = O (n ^ {r}) \ quad \ forall r> -1}

es equivalente a la hipótesis de Riemann, y luego Edmund Landau ^[16] comentó (justo después del artículo de Franel) que la declaración

{\ displaystyle \ sum _ {k = 1} ^ {m_ {n}} | d_ {k, n} | = O (n ^ {r}) \ quad \ forall r> 1/2}

También es equivalente a la hipótesis de Riemann.

Siguiente termino [ editar ]

Existe un algoritmo sorprendentemente simple para generar los términos de F _n en orden tradicional (ascendente) o en orden no tradicional (descendente). El algoritmo calcula cada entrada sucesiva en términos de las dos entradas anteriores usando la propiedad mediant dada anteriormente. Si a/b y c/d son las dos entradas dadas, y p/q es la siguiente entrada desconocida, entonces c/d  =  a  +  p/b  +  q . Como c/d está en los términos más bajos, debe haber un entero kde modo que kc  =  a  +  p y kd  =  b  +  q , dando p  =  kc  -  a y q  =  kd  -  b . Si consideramos que p y q son funciones de k , entonces

$${\ displaystyle {\ frac {p (k)} {q (k)}} - {\ frac {c} {d}} = {\ frac {cb-da} {d (kd-b)}}}

de modo que cuanto mayor sea k , más p/q se aproxima a c/d .

Para dar el siguiente término en la secuencia k debe ser lo más grande posible, sujeto a kd  -  b  ≤  n (ya que solo estamos considerando números con denominadores no mayores que n ), por lo que k es el mayor entero ≤  n  +  b/d . Poner este valor de k nuevamente en las ecuaciones para p y q da

$${\ displaystyle p = \ left \ lfloor {\ frac {n + b} {d}} \ right \ rfloor ca}

$${\ displaystyle q = \ left \ lfloor {\ frac {n + b} {d}} \ right \ rfloor db}

Esto se implementa en Python como:

def  farey_function ( n ,  descendente = Falso ): 
    "" "Imprima la secuencia n. ° de Farey, ya sea ascendente o descendente." "" 
    a ,  b ,  c ,  d  =  0 ,  1 ,  1 ,  n 
    si es  descendente :  
        a ,  c  =  1 ,  n - 1 
    imprime  " % d / % d "  %  ( a , b ) 
    mientras que  ( c  <= n  y  no  descendente )  o  ( un  >  0  y  descendente ): 
        k  =  int (( n  +  b )  /  d ) 
        un ,  b ,  c ,  d  =  c ,  d ,  ( k * c - a ),  ( k * d - b ) 
        imprima  " % d / % d "  %  (a , b )

Las búsquedas de fuerza bruta para soluciones a las ecuaciones diofánticas en los racionales a menudo pueden aprovechar la serie de Farey (para buscar solo formas reducidas). Las líneas marcadas (*) también pueden modificarse para incluir cualquiera de los dos términos adyacentes para generar términos más grandes (o más pequeños) que un término dado.