OCEANOGRAFÍA FÍSICA

 solitón es un paquete de ondassolitarias que se auto-refuerza y mantiene su forma mientras se propaga a una velocidad constante. Los solitones son causados ​​por una cancelación de efectos no lineales y dispersivos en el medio. (El término "efectos dispersivos" se refiere a una propiedad de ciertos sistemas donde la velocidad de las ondas varía según la frecuencia). Los solitones son las soluciones de una clase generalizada de ecuaciones diferenciales parciales dispersivas débilmente no lineales que describen sistemas físicos.

El fenómeno del solitón fue descrito por primera vez en 1834 por John Scott Russell (1808–1882) quien observó una ola solitaria en el Canal de la Unión en Escocia. Reprodució el fenómeno en un tanque de olas y lo llamó " Ola de traducción ".

Onda solitaria en un canal de onda delaboratorio.

Definición [ editar ]

Una definición única y consensuada de un solitón es difícil de encontrar. Drazin y Johnson (1989 , p. 15) atribuyen tres propiedades a los solitones:

1. Son de forma permanente;
2. Están localizados dentro de una región;
3. Pueden interactuar con otros solitones y emerger de la colisión sin cambios, excepto por un cambio de fase .

Existen definiciones más formales, pero requieren matemáticas sustanciales. Además, algunos científicos usan el término solitón para fenómenos que no tienen estas tres propiedades (por ejemplo, las " balas de luz " de la óptica no lineal a menudo se llaman solitones a pesar de perder energía durante la interacción). ^[1]

Explicación [ editar ]

Un solitón de envoltura secante (sech) hiperbólicopara ondas de agua: la línea azul es la señal portadora , mientras que la línea roja es el solitón de envoltura .

La dispersión y la no linealidad pueden interactuar para producir formas de onda permanentes y localizadas . Considere un pulso de luz que viaja en vidrio. Se puede pensar en este pulso como una luz de varias frecuencias diferentes. Dado que el vidrio muestra dispersión, estas diferentes frecuencias viajan a diferentes velocidades y, por lo tanto, la forma del pulso cambia con el tiempo. Sin embargo, también se produce el efecto Kerr no lineal ; El índice de refracción de un material a una frecuencia dada depende de la amplitud o fuerza de la luz. Si el pulso tiene la forma correcta, el efecto Kerr cancela exactamente el efecto de dispersión, y la forma del pulso no cambia con el tiempo, por lo tanto es un solitón. Ver soliton (óptica) para una descripción más detallada.

Muchos modelos con solución exacta tienen soluciones de solitones, incluida la ecuación de Korteweg-de Vries , la ecuación de Schrödinger no lineal , la ecuación de Schrödinger no lineal acoplada y la ecuación de sine-Gordon . Las soluciones de solitón se obtienen típicamente por medio de la transformada de dispersión inversa , y deben su estabilidad a la integrabilidad de las ecuaciones de campo. La teoría matemática de estas ecuaciones es un campo amplio y muy activo de la investigación matemática.

Algunos tipos de diámetros de marea , un fenómeno de ola de algunos ríos, incluido el río Severn , son "irregulares": un frente de onda seguido de un tren de solitones. Otros solitones se producen como las olas internas submarinas , iniciadas por la topografía del fondo marino , que se propagan en la picnoclina oceánica . También existen solitones atmosféricos, como la nube de la gloria matutina del Golfo de Carpentaria , donde los solitones de presión que viajan en una capa de inversión de temperatura producen vastas nubes de rodilloslineales . El modelo de solitón reciente y no ampliamente aceptado en neurociencia.propone explicar la conducción de la señal dentro de las neuronas como solitones de presión.

Un solitón topológico , también llamado defecto topológico, es cualquier solución de un conjunto de ecuaciones diferenciales parciales que es estable contra la descomposición de la "solución trivial". La estabilidad del solitón se debe a restricciones topológicas, en lugar de la integrabilidad de las ecuaciones de campo. Las restricciones surgen casi siempre porque las ecuaciones diferenciales deben obedecer a un conjunto de condiciones de límites, y el límite tiene un grupo de homotopía no trivial , preservado por las ecuaciones diferenciales. Por lo tanto, las soluciones de ecuaciones diferenciales se pueden clasificar en clases de homotopía .

Ninguna transformación continua asigna una solución en una clase de homotopía a otra. Las soluciones son realmente distintas y mantienen su integridad, incluso frente a fuerzas extremadamente poderosas. Los ejemplos de solitones topológicos incluyen la dislocación de tornillo en una red cristalina , la cadena de Dirac y el monopolo magnético en el electromagnetismo , el modelo de Skyrmion y Wess-Zumino-Witten en la teoría del campo cuántico , el cielo magnético en la física de la materia condensada y las cuerdas cósmicas y Muros de dominio en la cosmología .

Historia [ editar ]

En 1834, John Scott Russell describe su ola de traducción . ^{[nb 1]} El descubrimiento se describe aquí con las propias palabras de Scott Russell: ^{[nb 2]}

Estaba observando el movimiento de un bote que fue arrastrado rápidamente a lo largo de un estrecho canal por un par de caballos, cuando el bote se detuvo repentinamente, no así la masa de agua en el canal que había puesto en movimiento; se acumuló alrededor de la proa de la embarcación en un estado de violenta agitación, y luego, repentinamente, dejándola atrás, avanzó a gran velocidad, asumiendo la forma de una gran elevación solitaria, un montón de agua redondeado, liso y bien definido, que continuó Su curso a lo largo del canal aparentemente sin cambio de forma o disminución de la velocidad. Lo seguí a caballo y lo adelanté aún rodando a una velocidad de unas ocho o nueve millas por hora, conservando su figura original de unos treinta pies de largo y un pie a un pie y medio de altura. Su altura disminuyó gradualmente, y después de una persecución de una o dos millas, lo perdí en los devanados del canal. Así, en el mes de agosto de 1834, fue mi primera entrevista casual con ese fenómeno singular y hermoso que llamé la Ola de la Traducción.^[2]

Scott Russell pasó algún tiempo haciendo investigaciones prácticas y teóricas de estas olas. Construyó tanques de olas en su casa y notó algunas propiedades clave:

• Las ondas son estables y pueden viajar distancias muy grandes (las ondas normales tienden a aplanarse o inclinarse y caer)
• La velocidad depende del tamaño de la ola y su ancho en la profundidad del agua.
• A diferencia de las ondas normales, nunca se fusionarán, por lo que una pequeña ola es superada por una grande, en lugar de las dos.
• Si una ola es demasiado grande para la profundidad del agua, se divide en dos, una grande y otra pequeña.

El trabajo experimental de Scott Russell parecía estar en desacuerdo con las teorías de la hidrodinámica de Isaac Newton y Daniel Bernoulli . George Biddell Airy y George Gabriel Stokes tuvieron dificultades para aceptar las observaciones experimentales de Scott Russell porque no podían explicarse por las teorías de las olas de agua existentes. Sus contemporáneos pasaron un tiempo intentando extender la teoría, pero tomaría hasta la década de 1870 antes de que Joseph Boussinesq y Lord Rayleigh publicaran un tratamiento y soluciones teóricas. ^{[nb 3]} En 1895, Diederik Korteweg y Gustav de Vries proporcionaron lo que ahora se conoce como elEcuación de Korteweg – de Vries , que incluye soluciones de ondas solitarias y de ondas cnoidales periódicas . ^{[3] [nb 4]}

Una animación de los adelantamientos de dos ondas solitarias según la ecuación de Benjamin-Bona-Mahony o la ecuación de BBM, una ecuación modelo para (entre otros) ondas de gravedad de superficie larga . Las alturas de onda de las ondas solitarias son 1.2 y 0.6, respectivamente, y sus velocidades son 1.4 y 1.2. 
El gráfico superior es para un marco de referencia que se mueve con la velocidad promedio de las ondas solitarias. 
El gráfico inferior (con una escala vertical diferente y en un marco de referencia estacionario) muestra la cola oscilatoria producida por la interacción. ^[4] Por lo tanto, las soluciones de onda solitaria de la ecuación de BBM no son solitones.

En 1965, Norman Zabusky de Bell Labs y Martin Kruskal de la Universidad de Princeton demostraron por primera vez el comportamiento de solitones en medios sujetos a la ecuación de Korteweg – de Vries (ecuación de KdV) en una investigación computacional utilizando un enfoque de diferencias finitas . También mostraron cómo este comportamiento explicaba el desconcertante trabajo anterior de Fermi, Pasta, Ulam y Tsingou. ^[5]

En 1967, Gardner, Greene, Kruskal y Miura descubrieron una transformada de dispersión inversa que permite la solución analítica de la ecuación de KdV. ^[6] El trabajo de Peter Lax sobre los pares de Lax y la ecuación de Lax ha extendido esto a la solución de muchos sistemas relacionados que generan solitones.

Tenga en cuenta que los solitones son, por definición, inalterados en forma y velocidad por una colisión con otros solitones. ^[7] Por lo tanto, las ondas solitarias en la superficie del agua están cerca de los solitones, pero no exactamente, después de la interacción de dos ondas solitarias (en colisión o adelantamientos), han cambiado un poco en amplitud y se deja un oscilatorio residual. ^[8]

Los solitones también se estudian en mecánica cuántica, gracias al hecho de que podrían proporcionar una nueva base a través del programa inacabado de Broglie , conocido como "Teoría de doble solución" o "Mecánica de ondas no lineales". Esta teoría, desarrollada por de Broglie en 1927 y revivida en la década de 1950, es la continuación natural de sus ideas desarrolladas entre 1923 y 1926, que extendió la dualidad onda-partículaintroducida por Einstein para los cuantos de luz , a todas las partículas de materia.

Solitones en fibra óptica [ editar ]

Ver también: Soliton (óptica).

Se ha realizado mucha experimentación utilizando solitones en aplicaciones de fibra óptica. Los solitones en un sistema de fibra óptica se describen mediante las ecuaciones de Manakov . La estabilidad inherente de los solitones hace posible la transmisión a larga distancia sin el uso de repetidores , y también podría duplicar la capacidad de transmisión. ^[9]

Año	Descubrimiento
1973	Akira Hasegawa, de AT&T Bell Labs, fue el primero en sugerir que los solitones podrían existir en las fibras ópticas , debido al equilibrio entre la modulación de la autofase y la dispersión anómala . [10]También en 1973, Robin Bullough hizo el primer informe matemático de la existencia de solitones ópticos. También propuso la idea de un sistema de transmisión basado en solitones para aumentar el rendimiento de las telecomunicaciones ópticas .
1987	Emplit et al. (1987)  - de las Universidades de Bruselas y Limoges - realizó la primera observación experimental de la propagación de un solitón oscuro , en una fibra óptica.
1988	Linn Mollenauer y su equipo transmitieron los pulsos de solitón a más de 4.000 kilómetros utilizando un fenómeno llamado efecto Raman , que lleva el nombre de Sir CV Raman, quien lo describió por primera vez en la década de 1920, para proporcionar ganancia óptica en la fibra.
1991	Un equipo de investigación de Bell Labs transmitió solitones sin errores a 2.5 gigabits por segundo a lo largo de más de 14,000 kilómetros, utilizando amplificadores de fibra óptica de erbio (segmentos de fibra óptica empalmados que contienen el erbio del elemento de tierras raras). Los láseres de bomba, acoplados a los amplificadores ópticos, activan el erbio, que energiza los pulsos de luz.
1998	Thierry Georges y su equipo en France Telecom R&D Center, combinando solitones ópticos de diferentes longitudes de onda ( multiplexado por división de longitud de onda ), demostraron unatransmisión de datos compuesta de 1 terabit por segundo (1,000,000,000,000 unidades de información por segundo), que no debe confundirse con Terabit Ethernet. Sin embargo, los impresionantes experimentos anteriores no se han traducido a implementaciones de sistemas de solitones comerciales reales, ya sea en sistemas terrestres o submarinos, principalmente debido a la fluctuación de Gordon-Haus (GH) . La fluctuación de fase de GH requiere soluciones compensatorias sofisticadas y costosas que, en última instancia, hacen que la transmisión de solitones en el campo multiplexación por división de longitud de onda densa (DWDM) no sea atractiva, en comparación con el paradigma convencional de no retorno a cero / retorno a cero. Además, la probable adopción futura de los formatos QAM / cambio de fase más eficientes espectralmente hace que la transmisión de solitones sea aún menos viable, debido al efecto Gordon-Mollenauer. En consecuencia, el solitón de transmisión de fibra óptica de larga distancia ha sido una curiosidad de laboratorio.
2000	Cundiff predijo la existencia de un vector de solitón en una cavidad de fibra de birrefringencia en modo pasivo de bloqueo a través de un espejo absorbente de semiconductor saturable (SESAM). El estado de polarización de un vector de este tipo podría estar girando o bloqueando dependiendo de los parámetros de la cavidad. [11]
2008	DY Tang et al. Observó una nueva forma de vector de orden superior soliton desde las perspectivas de experimentos y simulaciones numéricas. Su grupo ha investigado diferentes tipos de solitones vectoriales y el estado de polarización de los solitones vectoriales. [12]

Solitones en la biología [ editar ]

Los solitones pueden ocurrir en las proteínas ^[13] y en el ADN. ^{[14] Los} solitones están relacionados con el movimiento colectivo de baja frecuencia en proteínas y ADN . ^[15]

Un modelo recientemente desarrollado en neurociencia propone que las señales, en forma de ondas de densidad, se realicen dentro de las neuronas en forma de solitones. ^{[16] [17] [18]}

Solitones en imanes [ editar ]

En los imanes, también existen diferentes tipos de solitones y otras ondas no lineales. ^[19] Estos solitones magnéticos son una solución exacta de ecuaciones diferenciales no lineales clásicas: ecuaciones magnéticas, por ejemplo, la ecuación de Landau-Lifshitz , el modelo continuo de Heisenberg , la ecuación de Ishimori , la ecuación de Schrödinger no lineal y otras.

Bions [ editar ]

El estado enlazado de dos solitones se conoce como bion , ^{[20] [21] [22]} o en sistemas donde el estado enlazado oscila periódicamente, un respiro .

En la teoría de campos, bion usualmente se refiere a la solución del modelo Born-Infeld . El nombre parece haber sido acuñado por GW Gibbons para distinguir esta solución del solitón convencional, entendida como una solución regular de energía finita (y generalmente estable) de una ecuación diferencial que describe algún sistema físico. ^[23] La palabra regularSignifica una solución suave que no tiene ninguna fuente. Sin embargo, la solución del modelo Born-Infeld todavía tiene una fuente en forma de una función de Dirac-delta en el origen. Como consecuencia, muestra una singularidad en este punto (aunque el campo eléctrico es regular en todas partes). En algunos contextos físicos (por ejemplo, la teoría de cuerdas) esta característica puede ser importante, lo que motivó la introducción de un nombre especial para esta clase de solitones.

Por otro lado, cuando se agrega la gravedad (es decir, cuando se considera el acoplamiento del modelo Born-Infeld a la relatividad general), la solución correspondiente se llama EBIon , donde "E" significa Einstein.

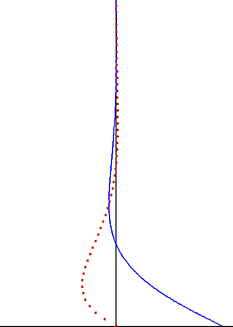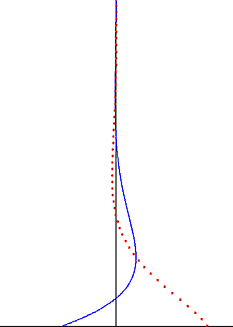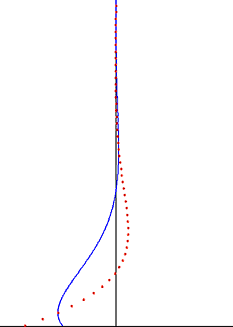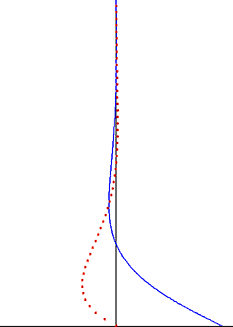
 el problema de Stokes también conocido como segundo problema de Stokes o, a veces, denominado capa límite de Stokes o capa límite de oscilación es un problema para determinar el flujo creado por una superficie sólida oscilante, llamada Sir George Stokes . Esto se considera como uno de los problemas inestables más simples que tienen una solución exacta para las ecuaciones de Navier-Stokes ^[1] [2] . En flujo turbulento , esto todavía se denomina capa límite de Stokes, pero ahora uno tiene que confiar en experimentos , simulaciones numéricas o métodos aproximados.Con el fin de obtener información útil sobre el flujo.

El problema de Stokes en un fluido viscoso debido a la oscilación armónica de una placa rígida plana (borde negro inferior). Velocidad (línea azul) y excursión de partículas (puntos rojos) en función de la distancia a la pared.

Descripción del flujo ^[3] [4] [ editar ]

Considere una placa infinitamente larga que está oscilando con una velocidad $${\ displaystyle U \ cos \ omega t} en el $${\ displaystyle x} dirección, que se encuentra en $${\ displaystyle y = 0} en un dominio infinito de fluido, donde $${\ displaystyle \ omega}Es la frecuencia de las oscilaciones. Las incomprensibles ecuaciones de Navier-Stokes se reducen a

$${\ displaystyle {\ frac {\ parcial u} {\ parcial t}} = \ nu {\ frac {\ parcial ^ {2} u} {\ parcial y ^ {2}}}}

dónde $${\ displaystyle \ nu}Es la viscosidad cinemática . El gradiente de presión no entra en el problema. La condición inicial, antideslizante en la pared es

$${\ displaystyle u (0, t) = U \ cos \ omega t, \ quad u (\ infty, t) = 0,}

y la segunda condición límite se debe al hecho de que el movimiento en $${\ displaystyle y = 0}no se siente en el infinito. El flujo solo se debe al movimiento de la placa, no hay un gradiente de presión impuesto.

Solución ^[5] [6] [ editar ]

La condición inicial no es necesaria debido a la periodicidad. Dado que tanto la ecuación como las condiciones de contorno son lineales, la velocidad puede escribirse como la parte real de alguna función compleja.

$${\ displaystyle u = U \ Re \ left [e ^ {i \ omega t} f (y) \ right]}

porque $${\ displaystyle \ cos \ omega t = \ Re e ^ {i \ omega t}}.

Sustituir esto en la ecuación diferencial parcial lo reduce a la ecuación diferencial ordinaria

$${\ displaystyle f '' - {\ frac {i \ omega} {\ nu}} f = 0}

con condiciones de contorno

$${\ displaystyle f (0) = 1, \ quad f (\ infty) = 0}

La solución al problema anterior es

$${\ displaystyle f (y) = \ exp \ left [- {\ frac {1 + i} {\ sqrt {2}}} {\ sqrt {\ frac {\ omega} {\ nu}}} y \ right] }

$${\ displaystyle u (y, t) = Ue ^ {- {\ sqrt {\ frac {\ omega} {2 \ nu}}} y} \ cos \ left (\ omega t - {\ sqrt {\ frac {\ omega} {2 \ nu}}} y \ right)}

La perturbación creada por la placa oscilante se desplaza como una onda transversal a través del fluido, pero está altamente amortiguada por el factor exponencial. La profundidad de penetración.$${\ displaystyle \ delta = {\ sqrt {2 \ nu / \ omega}}} de esta onda disminuye con la frecuencia de la oscilación, pero aumenta con la viscosidad cinemática del fluido.

La fuerza por unidad de área ejercida sobre la placa por el fluido es

$${\ displaystyle F = \ mu \ left ({\ frac {\ partial u} {\ partial y}} \ right) _ {y = 0} = {\ sqrt {\ rho \ omega \ mu}} U \ cos \ izquierda (\ omega t - {\ frac {\ pi} {4}} \ derecha)}

Hay un cambio de fase entre la oscilación de la placa y la fuerza creada.

Oscilaciones de vorticidad cerca del límite [ editar ]

Una observación importante de la solución de Stokes para el flujo de Stokes oscilante es que las oscilaciones de vorticidad están confinadas a una capa límite delgada y exponencialmente húmeda cuando se aleja de la pared. ^[7] Esta observación también es válida para el caso de una capa límite turbulenta. Fuera de la capa límite de Stokes, que a menudo es la mayor parte del volumen del líquido, las oscilaciones de vorticidad pueden ser ignoradas. Para una buena aproximación, las oscilaciones de la velocidad del flujo son irrotacionales fuera de la capa límite, y la teoría del flujo potencial puede aplicarse a la parte oscilatoria del movimiento. Esto simplifica significativamente la solución de estos problemas de flujo y, a menudo, se aplica en las regiones de flujo irrotacional deOndas sonoras y ondas de agua .

Flujo debido a un gradiente de presión oscilante cerca de una placa rígida plana [ editar ]

La capa límite de Stokes debido a la oscilación sinusoidal de la velocidad de flujo del campo lejano. La velocidad horizontal es la línea azul, y las excursiones de partículas horizontales correspondientes son los puntos rojos.

El caso para un flujo de campo lejano oscilante , con la placa mantenida en reposo, se puede construir fácilmente a partir de la solución anterior para una placa oscilante mediante el uso de una superposición lineal de soluciones. Considere una oscilación de velocidad uniforme$${\ displaystyle u (\ infty, t) = U _ {\ infty} \ cos \ omega t} lejos de la placa y una velocidad de fuga en la placa $${\ displaystyle u (0, t) = 0}. A diferencia del fluido estacionario en el problema original, el gradiente de presión aquí en el infinito debe ser una función armónica del tiempo. La solución es entonces dada por

$${\ displaystyle u (y, t) = U _ {\ infty} \ left [\, \ cos \ omega t - {\ text {e}} ^ {- {\ sqrt {\ frac {\ omega} {2 \ nu }}} y} \, \ cos \ left (\ omega t - {\ sqrt {\ frac {\ omega} {2 \ nu}}} y \ right) \ right],

que es cero en la pared z = 0 , correspondiente a la condición de no deslizamiento para una pared en reposo. Esta situación se encuentra a menudo en las ondas de sonido cerca de una pared sólida, o por el movimiento fluido cerca del fondo marino en las ondas de agua . La vorticidad, para el flujo oscilante cerca de una pared en reposo, es igual a la vorticidad en el caso de una placa oscilante pero de signo opuesto.

Problema de Stokes en geometría cilíndrica [ editar ]

Oscilación de torsión [ editar ]

Considera un cilindro de radio infinitamente largo. $${\ displaystyle a} Exhibiendo oscilación torsional con velocidad angular. $${\ displaystyle \ Omega \ cos \ omega t} dónde $${\ displaystyle \ omega}es la frecuencia Entonces la velocidad está dada por ^[8]

$${\ displaystyle v _ {\ theta} = a \ Omega \ \ Re \ left [{\ frac {K_ {1} (r {\ sqrt {i \ omega / \ nu}})} {K_ {1} (a { \ sqrt {i \ omega / \ nu}})}} e ^ {i \ omega t} \ right]}

dónde $${\ displaystyle K_ {1}} Es la función de Bessel modificada del segundo tipo.

Oscilación axial [ editar ]

Si el cilindro oscila en la dirección axial con velocidad. $${\ displaystyle U \ cos \ omega t}, entonces el campo de velocidad es

$${\ displaystyle u = U \ \ Re \ left [{\ frac {K_ {0} (r {\ sqrt {i \ omega / \ nu}})} {K_ {0} (a {\ sqrt {i \ omega / \ nu}})}} e ^ {i \ omega t} \ right]}

dónde $${\ displaystyle K_ {0}} Es la función de Bessel modificada del segundo tipo.

Flujo de Stokes-Couette ^[9] [ editar ]

En el flujo de Couette , en lugar del movimiento de traslación de una de las placas, se ejecutará una oscilación de un plano. Si tenemos una pared inferior en reposo en$${\ displaystyle y = 0} y la pared superior en $${\ displaystyle y = h} Está ejecutando un movimiento oscilatorio con velocidad. $${\ displaystyle U \ cos \ omega t}, entonces el campo de velocidad está dado por

$${\ displaystyle u = U \ \ Re \ left \ {{\ frac {\ sin ky} {\ sin kh}} \ right \}, \ quad {\ text {where}} \ quad k = {\ frac {1 + i} {\ sqrt {2}}} {\ sqrt {\ frac {\ omega} {\ nu}}}.}

La fuerza de fricción por unidad de área en el plano móvil es $${\ displaystyle - \ mu U \ Re \ {k \ cot kh \}} y en el plano fijo es $${\ displaystyle \ mu U \ Re \ {k \ csc kh \}}.