Del en coordenadas cilíndricas y esféricas.

Esta es una lista de algunas fórmulas de cálculo vectorial para trabajar con sistemas de coordenadas curvilíneascomunes .

Notas [ editar ]

Este artículo utiliza la notación estándar ISO 80000-2 , que reemplaza a la ISO 31-11 , para coordenadas esféricas (otras fuentes pueden revertir las definiciones de θ y φ ):
- El ángulo polar se denota con θ : es el ángulo entre el eje z y el vector radial que conecta el origen con el punto en cuestión.
- El ángulo azimutal se denota por φ : es el ángulo entre el eje x y la proyección del vector radial sobre el plano xy .
La función atan2 ( y , x ) se puede usar en lugar de la función matemática arctan ( y / x ) debido a su dominioe imagen . La función arctan clásica tiene una imagen de (−π / 2, + π / 2) , mientras que atan2 se define para tener una imagen de (−π, π) .

Coordinar conversiones [ editar ]

Conversión entre coordenadas cartesianas, cilíndricas y esféricas ^[1]
		Desde
		cartesiano	Cilíndrico	Esférico
A	cartesiano	${\begin{aligned}x&=x\\y&=y\\z&=z\end{aligned}}$	${\begin{aligned}x&=\rho \cos \varphi \\y&=\rho \sin \varphi \\z&=z\end{aligned}}$	${\begin{aligned}x&=r\sin \theta \cos \varphi \\y&=r\sin \theta \sin \varphi \\z&=r\cos \theta \end{aligned}}$
	Cilíndrico	${\begin{aligned}\rho &={\sqrt {x^{2}+y^{2}}}\\\varphi &=\arctan \left({\frac {y}{x}}\right)\\z&=z\end{aligned}}$	${\begin{aligned}\rho &=\rho \\\varphi &=\varphi \\z&=z\end{aligned}}$	${\begin{aligned}\rho &=r\sin \theta \\\varphi &=\varphi \\z&=r\cos \theta \end{aligned}}$
	Esférico	${\begin{aligned}r&={\sqrt {x^{2}+y^{2}+z^{2}}}\\\theta &=\arctan \left({\frac {\sqrt {x^{2}+y^{2}}}{z}}\right)\\\varphi &=\arctan \left({\frac {y}{x}}\right)\end{aligned}}$	${\begin{aligned}r&={\sqrt {\rho ^{2}+z^{2}}}\\\theta &=\arctan {\left({\frac {\rho }{z}}\right)}\\\varphi &=\varphi \end{aligned}}$	${\begin{aligned}r&=r\\\theta &=\theta \\\varphi &=\varphi \end{aligned}}$

Conversiones de vectores unitarios [ editar ]

Conversión entre vectores unitarios en sistemas de coordenadas cartesianas, cilíndricas y esféricas en términos de coordenadas de *destino* ^[1]
	cartesiano	Cilíndrico	Esférico
cartesiano	N / A	${\begin{aligned}{\hat {\mathbf {x} }}&=\cos \varphi {\hat {\boldsymbol {\rho }}}-\sin \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {y} }}&=\sin \varphi {\hat {\boldsymbol {\rho }}}+\cos \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}$	${\begin{aligned}{\hat {\mathbf {x} }}&=\sin \theta \cos \varphi {\hat {\mathbf {r} }}+\cos \theta \cos \varphi {\hat {\boldsymbol {\theta }}}-\sin \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {y} }}&=\sin \theta \sin \varphi {\hat {\mathbf {r} }}+\cos \theta \sin \varphi {\hat {\boldsymbol {\theta }}}+\cos \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&=\cos \theta {\hat {\mathbf {r} }}-\sin \theta {\hat {\boldsymbol {\theta }}}\end{aligned}}$
Cilíndrico	${\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\frac {x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\frac {-y{\hat {\mathbf {x} }}+x{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}$	N / A	${\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\sin \theta {\hat {\mathbf {r} }}+\cos \theta {\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&=\cos \theta {\hat {\mathbf {r} }}-\sin \theta {\hat {\boldsymbol {\theta }}}\end{aligned}}$
Esférico	${\begin{aligned}{\hat {\mathbf {r} }}&={\frac {x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}+z{\hat {\mathbf {z} }}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\\{\hat {\boldsymbol {\theta }}}&={\frac {\left(x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}\right)z-\left(x^{2}+y^{2}\right){\hat {\mathbf {z} }}}{{\sqrt {x^{2}+y^{2}+z^{2}}}{\sqrt {x^{2}+y^{2}}}}}\\{\hat {\boldsymbol {\varphi }}}&={\frac {-y{\hat {\mathbf {x} }}+x{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\end{aligned}}$	${\begin{aligned}{\hat {\mathbf {r} }}&={\frac {\rho {\hat {\boldsymbol {\rho }}}+z{\hat {\mathbf {z} }}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\theta }}}&={\frac {z{\hat {\boldsymbol {\rho }}}-\rho {\hat {\mathbf {z} }}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\end{aligned}}$	N / A

Conversión entre vectores unitarios en sistemas de coordenadas cartesianas, cilíndricas y esféricas en términos de coordenadasde *origen*
	cartesiano	Cilíndrico	Esférico
cartesiano	N / A	${\begin{aligned}{\hat {\mathbf {x} }}&={\frac {x{\hat {\boldsymbol {\rho }}}-y{\hat {\boldsymbol {\varphi }}}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {y} }}&={\frac {y{\hat {\boldsymbol {\rho }}}+x{\hat {\boldsymbol {\varphi }}}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}$	${\begin{aligned}{\hat {\mathbf {x} }}&={\frac {x\left({\sqrt {x^{2}+y^{2}}}{\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}\right)-y{\sqrt {x^{2}+y^{2}+z^{2}}}{\hat {\boldsymbol {\varphi }}}}{{\sqrt {x^{2}+y^{2}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}}\\{\hat {\mathbf {y} }}&={\frac {y\left({\sqrt {x^{2}+y^{2}}}{\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}\right)+x{\sqrt {x^{2}+y^{2}+z^{2}}}{\hat {\boldsymbol {\varphi }}}}{{\sqrt {x^{2}+y^{2}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}}\\{\hat {\mathbf {z} }}&={\frac {z{\hat {\mathbf {r} }}-{\sqrt {x^{2}+y^{2}}}{\hat {\boldsymbol {\theta }}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\end{aligned}}$
Cilíndrico	${\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi {\hat {\mathbf {x} }}+\cos \varphi {\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}$	N / A	${\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\frac {\rho {\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\frac {z{\hat {\mathbf {r} }}-\rho {\hat {\boldsymbol {\theta }}}}{\sqrt {\rho ^{2}+z^{2}}}}\end{aligned}}$
Esférico	${\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta \left(\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\right)+\cos \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\theta }}}&=\cos \theta \left(\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\right)-\sin \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi {\hat {\mathbf {x} }}+\cos \varphi {\hat {\mathbf {y} }}\end{aligned}}$	${\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta {\hat {\boldsymbol {\rho }}}+\cos \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\theta }}}&=\cos \theta {\hat {\boldsymbol {\rho }}}-\sin \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\end{aligned}}$	N / A

Del formula [ editar ]

Tabla con la del operador en cartesiano, cilíndrico y coordenadas esféricas
Operación	Coordenadas cartesianas $(x, y, z)$	Coordenadas cilíndricas $(ρ, φ, z)$	Coordenadas esféricas $(r, θ, φ)$ , donde θ es la polar y $φ$ es el ángulo acimutal ^α
Campo vectorial $A$	$A_{x}{\hat {\mathbf {x} }}+A_{y}{\hat {\mathbf {y} }}+A_{z}{\hat {\mathbf {z} }}$	$A_{\rho }{\hat {\boldsymbol {\rho }}}+A_{\varphi }{\hat {\boldsymbol {\varphi }}}+A_{z}{\hat {\mathbf {z} }}$	$A_{r}{\hat {\mathbf {r} }}+A_{\theta }{\hat {\boldsymbol {\theta }}}+A_{\varphi }{\hat {\boldsymbol {\varphi }}}$
Gradiente $\nabla f$ ^[1]	${\partial f \over \partial x}{\hat {\mathbf {x} }}+{\partial f \over \partial y}{\hat {\mathbf {y} }}+{\partial f \over \partial z}{\hat {\mathbf {z} }}$	${\partial f \over \partial \rho }{\hat {\boldsymbol {\rho }}}+{1 \over \rho }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}}+{\partial f \over \partial z}{\hat {\mathbf {z} }}$	${\partial f \over \partial r}{\hat {\mathbf {r} }}+{1 \over r}{\partial f \over \partial \theta }{\hat {\boldsymbol {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}}$
Divergencia $\nabla \cdot A$ ^[1]	${\partial A_{x} \over \partial x}+{\partial A_{y} \over \partial y}+{\partial A_{z} \over \partial z}$	${1 \over \rho }{\partial \left(\rho A_{\rho }\right) \over \partial \rho }+{1 \over \rho }{\partial A_{\varphi } \over \partial \varphi }+{\partial A_{z} \over \partial z}$	${1 \over r^{2}}{\partial \left(r^{2}A_{r}\right) \over \partial r}+{1 \over r\sin \theta }{\partial \over \partial \theta }\left(A_{\theta }\sin \theta \right)+{1 \over r\sin \theta }{\partial A_{\varphi } \over \partial \varphi }$
Curl $\nabla \times A$ ^[1]	${\begin{aligned}\left({\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\right)&{\hat {\mathbf {x} }}\\+\left({\frac {\partial A_{x}}{\partial z}}-{\frac {\partial A_{z}}{\partial x}}\right)&{\hat {\mathbf {y} }}\\+\left({\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}\right)&{\hat {\mathbf {z} }}\end{aligned}}$	${\begin{aligned}\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right)&{\hat {\boldsymbol {\rho }}}\\+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right)&{\hat {\boldsymbol {\varphi }}}\\{}+{\frac {1}{\rho }}\left({\frac {\partial \left(\rho A_{\varphi }\right)}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \varphi }}\right)&{\hat {\mathbf {z} }}\end{aligned}}$	${\begin{aligned}{\frac {1}{r\sin \theta }}\left({\frac {\partial }{\partial \theta }}\left(A_{\varphi }\sin \theta \right)-{\frac {\partial A_{\theta }}{\partial \varphi }}\right)&{\hat {\mathbf {r} }}\\{}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}-{\frac {\partial }{\partial r}}\left(rA_{\varphi }\right)\right)&{\hat {\boldsymbol {\theta }}}\\{}+{\frac {1}{r}}\left({\frac {\partial }{\partial r}}\left(rA_{\theta }\right)-{\frac {\partial A_{r}}{\partial \theta }}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}$
Operador de Laplace $\nabla 2 f \equiv ∆ f$ ^[1]	${\partial ^{2}f \over \partial x^{2}}+{\partial ^{2}f \over \partial y^{2}}+{\partial ^{2}f \over \partial z^{2}}$	${1 \over \rho }{\partial \over \partial \rho }\left(\rho {\partial f \over \partial \rho }\right)+{1 \over \rho ^{2}}{\partial ^{2}f \over \partial \varphi ^{2}}+{\partial ^{2}f \over \partial z^{2}}$	${1 \over r^{2}}{\partial \over \partial r}\!\left(r^{2}{\partial f \over \partial r}\right)\!+\!{1 \over r^{2}\!\sin \theta }{\partial \over \partial \theta }\!\left(\sin \theta {\partial f \over \partial \theta }\right)\!+\!{1 \over r^{2}\!\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}$
Vector laplaciano $\nabla 2 A \equiv ∆ A$	$\nabla ^{2}A_{x}{\hat {\mathbf {x} }}+\nabla ^{2}A_{y}{\hat {\mathbf {y} }}+\nabla ^{2}A_{z}{\hat {\mathbf {z} }}$	[espectáculo] - Ver haciendo clic en [Mostrar] -	[espectáculo] - Ver haciendo clic en [Mostrar] -
Material derivado ^α^[2] $(A \cdot \nabla) B$	$\mathbf {A} \cdot \nabla B_{x}{\hat {\mathbf {x} }}+\mathbf {A} \cdot \nabla B_{y}{\hat {\mathbf {y} }}+\mathbf {A} \cdot \nabla B_{z}{\hat {\mathbf {z} }}$	${\begin{aligned}\left(A_{\rho }{\frac {\partial B_{\rho }}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{\rho }}{\partial \varphi }}+A_{z}{\frac {\partial B_{\rho }}{\partial z}}-{\frac {A_{\varphi }B_{\varphi }}{\rho }}\right)&{\hat {\boldsymbol {\rho }}}\\+\left(A_{\rho }{\frac {\partial B_{\varphi }}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{\varphi }}{\partial \varphi }}+A_{z}{\frac {\partial B_{\varphi }}{\partial z}}+{\frac {A_{\varphi }B_{\rho }}{\rho }}\right)&{\hat {\boldsymbol {\varphi }}}\\+\left(A_{\rho }{\frac {\partial B_{z}}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{z}}{\partial \varphi }}+A_{z}{\frac {\partial B_{z}}{\partial z}}\right)&{\hat {\mathbf {z} }}\end{aligned}}$	[show] — View by clicking [show] —
Tensio divergencia $\nabla \cdot T$	[espectáculo] - Ver haciendo clic en [Mostrar] -	[espectáculo] - Ver haciendo clic en [Mostrar] -	[espectáculo] - Ver haciendo clic en [Mostrar] -
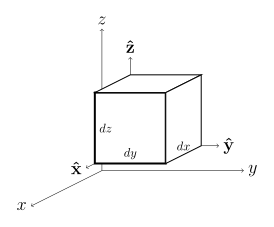
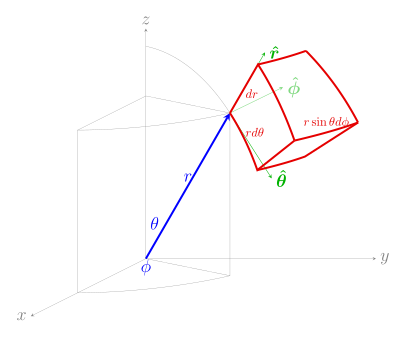
Desplazamiento diferencial $d ℓ$ ^[1]	$dx\,{\hat {\mathbf {x} }}+dy\,{\hat {\mathbf {y} }}+dz\,{\hat {\mathbf {z} }}$	$d\rho \,{\hat {\boldsymbol {\rho }}}+\rho \,d\varphi \,{\hat {\boldsymbol {\varphi }}}+dz\,{\hat {\mathbf {z} }}$	$dr\,{\hat {\mathbf {r} }}+r\,d\theta \,{\hat {\boldsymbol {\theta }}}+r\,\sin \theta \,d\varphi \,{\hat {\boldsymbol {\varphi }}}$
Área normal diferenciada $d S$	${\begin{aligned}dy\,dz&\,{\hat {\mathbf {x} }}\\{}+dx\,dz&\,{\hat {\mathbf {y} }}\\{}+dx\,dy&\,{\hat {\mathbf {z} }}\end{aligned}}$	${\begin{aligned}\rho \,d\varphi \,dz&\,{\hat {\boldsymbol {\rho }}}\\{}+d\rho \,dz&\,{\hat {\boldsymbol {\varphi }}}\\{}+\rho \,d\rho \,d\varphi &\,{\hat {\mathbf {z} }}\end{aligned}}$	${\begin{aligned}r^{2}\sin \theta \,d\theta \,d\varphi &\,{\hat {\mathbf {r} }}\\{}+r\sin \theta \,dr\,d\varphi &\,{\hat {\boldsymbol {\theta }}}\\{}+r\,dr\,d\theta &\,{\hat {\boldsymbol {\varphi }}}\end{aligned}}$
Volumen diferencial $dV$ ^[1]	$dx\,dy\,dz$	$\rho \,d\rho \,d\varphi \,dz$	$r^{2}\sin \theta \,dr\,d\theta \,d\varphi$

^ α Esta página utiliza

\theta

para el ángulo polar y

\varphi

Para el ángulo azimutal, que es la notación común en la física. La fuente que se utiliza para estas fórmulas utiliza.

\theta

para el ángulo azimutal y

\varphi

Para el ángulo polar, que es la notación matemática común. Para obtener las fórmulas matemáticas, cambiar

\theta

y

\varphi

en las fórmulas mostradas en la tabla anterior.

Reglas de cálculo no triviales [ editar ]

$\operatorname {div} \,\operatorname {grad} f\equiv \nabla \cdot \nabla f\equiv \nabla ^{2}f$
$\operatorname {curl} \,\operatorname {grad} f\equiv \nabla \times \nabla f=\mathbf {0}$
$\operatorname {div} \,\operatorname {curl} \mathbf {A} \equiv \nabla \cdot (\nabla \times \mathbf {A} )=0$
$\operatorname {curl} \,\operatorname {curl} \mathbf {A} \equiv \nabla \times (\nabla \times \mathbf {A} )=\nabla (\nabla \cdot \mathbf {A} )-\nabla ^{2}\mathbf {A}$ ( Fórmula de Lagrange para del)
$\nabla ^{2}(fg)=f\nabla ^{2}g+2\nabla f\cdot \nabla g+g\nabla ^{2}f$