SISTEMAS DE COORDENADAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Las coordenadas parabólicas son un sistema de coordenadas ortogonalbidimensional en el que las líneas de coordenadas son parábolas confocales . Una versión tridimensional de coordenadas parabólicas se obtiene girando el sistemabidimensional sobre el eje de simetría de las parábolas.

Las coordenadas parabólicas han encontrado muchas aplicaciones, por ejemplo, el tratamiento del efecto Stark y la teoría potencial de los bordes.

Bidimensionales coordenadas parabólicas [ editar ]

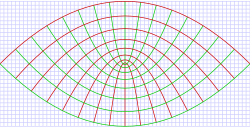
Coordenadas parabólicas bidimensionales $${\ displaystyle (\ sigma, \ tau)} Están definidas por las ecuaciones, en términos de coordenadas cartesianas:

$${\ displaystyle x = \ sigma \ tau}

$${\ displaystyle y = {\ frac {1} {2}} \ left (\ tau ^ {2} - \ sigma ^ {2} \ right)}

Las curvas de constante. $${\ displaystyle \ sigma} formar parabola confocal

$${\ displaystyle 2y = {\ frac {x ^ {2}} {\ sigma ^ {2}}} - \ sigma ^ {2}}

que se abren hacia arriba (es decir, hacia $${\ displaystyle + y}), mientras que las curvas de constante $${\ displaystyle \ tau} formar parabola confocal

$${\ displaystyle 2y = - {\ frac {x ^ {2}} {\ tau ^ {2}}} + \ tau ^ {2}}

que abren hacia abajo (es decir, hacia $${\ displaystyle -y}). Los focos de todas estas parábolas están localizados en el origen.

Factores de escala bidimensional [ editar ]

Los factores de escala para las coordenadas parabólicas. $${\ displaystyle (\ sigma, \ tau)} son iguales

$${\ displaystyle h _ {\ sigma} = h _ {\ tau} = {\ sqrt {\ sigma ^ {2} + \ tau ^ {2}}}}

Por lo tanto, el elemento infinitesimal del área es

$${\ displaystyle dA = \ left (\ sigma ^ {2} + \ tau ^ {2} \ right) d \ sigma d \ tau}

y los iguales laplacianos

$${\ displaystyle \ nabla ^ {2} \ Phi = {\ frac {1} {\ sigma ^ {2} + \ tau ^ {2}}} \ left ({\ frac {\ partial ^ {2} \ Phi} {\ partial \ sigma ^ {2}}} + {\ frac {\ partial ^ {2} \ Phi} {\ partial \ tau ^ {2}}} \ right)}

Otros operadores diferenciales tales como $${\ displaystyle \ nabla \ cdot \ mathbf {F}} y $${\ displaystyle \ nabla \ times \ mathbf {F}} Se puede expresar en las coordenadas. $${\ displaystyle (\ sigma, \ tau)}sustituyendo los factores de escala en las fórmulas generales que se encuentran en las coordenadas ortogonales.

Tridimensionales coordenadas parabólicas [ editar ]

Coordinar las superficies de las coordenadas parabólicas tridimensionales. El paraboloide rojo corresponde a τ = 2, el paraboloid azul corresponde a σ = 1, y el semiplano amarillo corresponde a φ = -60 °. Las tres superficies se intersecan en el punto P(mostrado como una esfera negra) con coordenadas cartesianas aproximadamente (1.0, -1.732, 1.5).

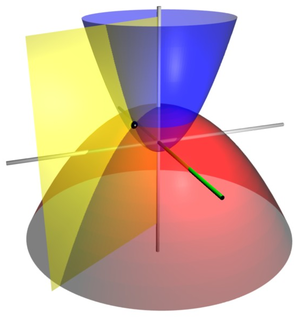
Las coordenadas parabólicas bidimensionales forman la base de dos conjuntos de coordenadas ortogonalestridimensionales . Las coordenadas cilíndricas parabólicasse producen proyectando en el$${\ displaystyle z}-dirección. La rotación sobre el eje de simetría de las parábolas produce un conjunto de paraboloides confocales, el sistema de coordenadas de las coordenadas parabólicas tridimensionales. Expresado en términos de coordenadas cartesianas:

$${\ displaystyle x = \ sigma \ tau \ cos \ varphi}

$${\ displaystyle y = \ sigma \ tau \ sin \ varphi}

$${\ displaystyle z = {\ frac {1} {2}} \ left (\ tau ^ {2} - \ sigma ^ {2} \ right)}

donde las parábola ahora están alineadas con la $${\ displaystyle z}-axis, sobre el que se realizó la rotación. Por lo tanto, el ángulo azimutal$${\ displaystyle \ phi} se define

$${\ displaystyle \ tan \ varphi = {\ frac {y} {x}}}

Las superficies de constante. $${\ displaystyle \ sigma} formar paraboloides confocales

$${\ displaystyle 2z = {\ frac {x ^ {2} + y ^ {2}} {\ sigma ^ {2}}} - \ sigma ^ {2}}

que se abren hacia arriba (es decir, hacia $${\ displaystyle + z}) mientras que las superficies de constante $${\ displaystyle \ tau} formar paraboloides confocales

$${\ displaystyle 2z = - {\ frac {x ^ {2} + y ^ {2}} {\ tau ^ {2}}} + \ tau ^ {2}}

que abren hacia abajo (es decir, hacia $${\ displaystyle -z}). Los focos de todos estos paraboloides se encuentran en el origen.

El tensor métrico riemanniano asociado con este sistema de coordenadas es

{\ displaystyle g_ {ij} = {\ begin {bmatrix} \ sigma ^ {2} + \ tau ^ {2} & 0 & 0 \\ 0 & \ sigma ^ {2} + \ tau ^ {2} & 0 \\ 0 & 0 & \ sigma ^ {2} \ tau ^ {2} \ end {bmatrix}}}

Tridimensionales factores de escala [ editar ]

Los factores de escala tridimensionales son:

$${\ displaystyle h _ {\ sigma} = {\ sqrt {\ sigma ^ {2} + \ tau ^ {2}}}}

$${\ displaystyle h _ {\ tau} = {\ sqrt {\ sigma ^ {2} + \ tau ^ {2}}}}

$${\ displaystyle h _ {\ varphi} = \ sigma \ tau}

Se ve que los factores de escala $${\ displaystyle h _ {\ sigma}} y $${\ displaystyle h _ {\ tau}}Son los mismos que en el caso bidimensional. El elemento de volumen infinitesimal es entonces

$${\ displaystyle dV = h _ {\ sigma} h _ {\ tau} h _ {\ varphi} \, d \ sigma \, d \ tau \, d \ varphi = \ sigma \ tau \ left (\ sigma ^ {2} + \ tau ^ {2} \ right) \, d \ sigma \, d \ tau \, d \ varphi}

y el laplaciano está dado por

$${\ displaystyle \ nabla ^ {2} \ Phi = {\ frac {1} {\ sigma ^ {2} + \ tau ^ {2}}} izquierda [{\ frac {1} {\ sigma}} {\ frac {\ partial} {\ partial \ sigma}} \ left (\ sigma {\ frac {\ partial \ Phi} {\ partial \ sigma}} \ right) + {\ frac {1} {\ tau}} {\ frac {\ partial} {\ partial \ tau}} \ left (\ tau {\ frac {\ partial \ Phi} {\ partial \ tau}} \ right) \ right] + {\ frac {1} {\ sigma ^ {2} \ tau ^ {2}}} {\ frac {\ partial ^ {2} \ Phi} {\ partial \ varphi ^ {2}}}}

Otros operadores diferenciales tales como $${\ displaystyle \ nabla \ cdot \ mathbf {F}} y $${\ displaystyle \ nabla \ times \ mathbf {F}} Se puede expresar en las coordenadas. $${\ displaystyle (\ sigma, \ tau, \ phi)}sustituyendo los factores de escala en las fórmulas generales que se encuentran en las coordenadas ortogonales.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Coordinar superficies de coordenadas parabólicas cilíndricas. El cilindro parabólico rojo corresponde a σ = 2, mientras que el cilindro parabólico amarillo corresponde a τ = 1. El plano azul corresponde a z = 2. Estas superficies se intersecan en el punto P (se muestra como una esfera negra), que tiene coordenadas cartesianas aproximadamente (2, -1.5, 2).

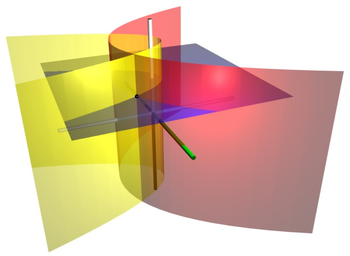
En matemáticas , las coordenadas cilíndricas parabólicas son un sistema de coordenadas ortogonales tridimensional que resulta de la proyección del sistema de coordenadas parabólicasbidimensional en la perpendicular$${\ displaystyle z}-dirección. Por lo tanto, las superficies coordinadas son cilindros parabólicos confocales . Las coordenadas cilíndricas parabólicas han encontrado muchas aplicaciones, por ejemplo, la teoría potencial de los bordes.

Definición básica [ editar ]

Sistema de coordenadas parabólicas que muestran curvas de constante σ y τ, los ejes horizontal y vertical son las coordenadas x e y respectivamente. Estas coordenadas se proyectan a lo largo del eje z, por lo que este diagrama se mantendrá para cualquier valor de la coordenada z.

Las coordenadas cilíndricas parabólicas ( σ , τ , z ) se definen en términos de las coordenadas cartesianas ( x , y , z ) por:

{\ displaystyle {\ begin {alineado} x & = \ sigma \ tau \\ y & = {\ frac {1} {2}} \ left (\ tau ^ {2} - \ sigma ^ {2} \ right) \\ z & = z \ end {alineado}}}

Las superficies de σ constantes forman cilindros parabólicos confocales.

$${\ displaystyle 2y = {\ frac {x ^ {2}} {\ sigma ^ {2}}} - \ sigma ^ {2}}

que se abren hacia + y , mientras que las superficies de τconstantes forman cilindros parabólicos confocales

$${\ displaystyle 2y = - {\ frac {x ^ {2}} {\ tau ^ {2}}} + \ tau ^ {2}}

que se abren en la dirección opuesta, es decir, hacia - y . Los focos de todos estos cilindros parabólicos están ubicados a lo largo de la línea definida por x = y = 0 . El radio r tiene una fórmula simple también

$${\ displaystyle r = {\ sqrt {x ^ {2} + y ^ {2}}} = {\ frac {1} {2}} \ left (\ sigma ^ {2} + \ tau ^ {2} \ Correcto)}

eso resulta útil para resolver la ecuación de Hamilton-Jacobi en coordenadas parabólicas para el problema de la fuerza central de la inversa al cuadrado de la mecánica ; Para más detalles, vea el artículo vectorial de Laplace-Runge-Lenz .

Factores de escala [ editar ]

Los factores de escala para las coordenadas cilíndricas parabólicas σ y τ son:

{\ displaystyle {\ begin {alineado} h _ {\ sigma} & = h _ {\ tau} = {\ sqrt {\ sigma ^ {2} + \ tau ^ {2}}} \\ h_ {z} & = 1 \ end {alineado}}}

Elementos diferenciales [ editar ]

El elemento infinitesimal del volumen es.

$${\ displaystyle dV = h _ {\ sigma} h _ {\ tau} h_ {z} d \ sigma d \ tau dz = (\ sigma ^ {2} + \ tau ^ {2}) d \ sigma \, d \ tau \, dz}

El desplazamiento diferencial está dado por:

$${\ displaystyle d \ mathbf {l} = {\ sqrt {\ sigma ^ {2} + \ tau ^ {2}}} \, d \ sigma \, {\ boldsymbol {\ hat {\ sigma}}} + { \ sqrt {\ sigma ^ {2} + \ tau ^ {2}}} \, d \ tau \, {\ boldsymbol {\ hat {\ tau}}} + dz \, \ mathbf {\ hat {z}} }

El área normal diferencial está dada por:

$${\ displaystyle d \ mathbf {S} = {\ sqrt {\ sigma ^ {2} + \ tau ^ {2}}} \, d \ tau \, dz {\ boldsymbol {\ hat {\ sigma}}} + {\ sqrt {\ sigma ^ {2} + \ tau ^ {2}}} \, d \ sigma \, dz {\ boldsymbol {\ hat {\ tau}}} + \ left (\ sigma ^ {2} + \ tau ^ {2} \ right) \, d \ sigma \, d \ tau \ mathbf {\ hat {z}}}

Del [ editar ]

Sea f un campo escalar. El gradiente está dado por

$${\ displaystyle \ nabla f = {\ frac {1} {\ sqrt {\ sigma ^ {2} + \ tau ^ {2}}}} {\ partial f \ over \ partial \ sigma} {\ boldsymbol {\ hat {\ sigma}}} + {\ frac {1} {\ sqrt {\ sigma ^ {2} + \ tau ^ {2}}}} {\ partial f \ over \ partial \ tau} {\ boldsymbol {\ hat {\ tau}}} + {\ partial f \ over \ partial z} \ mathbf {\ hat {z}}}

El laplaciano está dado por

$${\ displaystyle \ nabla ^ {2} f = {\ frac {1} {\ sigma ^ {2} + \ tau ^ {2}}} \ left ({\ frac {\ partial ^ {2} f} {\ parcial \ sigma ^ {2}}} + {\ frac {\ parcial ^ {2} f} {\ parcial \ tau ^ {2}}} \ derecha) + {\ frac {\ parcial ^ {2} f} { \ parcial z ^ {2}}}}

Sea A un campo vectorial de la forma:

$${\ displaystyle \ mathbf {A} = A _ {\ sigma} {\ boldsymbol {\ hat {\ sigma}}} + A _ {\ tau} {\ boldsymbol {\ hat {\ tau}}} + A_ {z} \ mathbf {\ hat {z}}}

La divergencia está dada por

$${\ displaystyle \ nabla \ cdot \ mathbf {A} = {\ frac {1} {\ sigma ^ {2} + \ tau ^ {2}}} \ left ({\ partial ({\ sqrt {\ sigma ^ { 2} + \ tau ^ {2}}} A _ {\ sigma}) \ over \ partial \ sigma} + {\ partial ({\ sqrt {\ sigma ^ {2} + \ tau ^ {2}}} A_ { \ tau}) \ over \ partial \ tau} \ right) + {\ partial A_ {z} \ over \ partial z}}

El rizo esta dado por

${\displaystyle \nabla \times \mathbf {A} =\left({\frac {1}{\sqrt {\sigma ^{2}+\tau ^{2}}}}{\frac {\partial A_{z}}{\partial \tau }}-{\frac {\partial A_{\tau }}{\partial z}}\right){\boldsymbol {\hat {\sigma }}}-\left({\frac {1}{\sqrt {\sigma ^{2}+\tau ^{2}}}}{\frac {\partial A_{z}}{\partial \sigma }}-{\frac {\partial A_{\sigma }}{\partial z}}\right){\boldsymbol {\hat {\tau }}}+{\frac {1}{\sigma ^{2}+\tau ^{2}}}\left({\frac {\partial \left({\sqrt {\sigma ^{2}+\tau ^{2}}}A_{\sigma }\right)}{\partial \tau }}-{\frac {\partial \left({\sqrt {\sigma ^{2}+\tau ^{2}}}A_{\tau }\right)}{\partial \sigma }}\right)\mathbf {\hat {z}} }$

Otros operadores diferenciales se pueden expresar en las coordenadas ( σ , τ ) sustituyendo los factores de escala en las fórmulas generales que se encuentran en las coordenadas ortogonales .

Relación con otros sistemas de coordenadas [ editar ]

Relación a coordenadas cilíndricas ( ρ , φ , z ) :

{\ displaystyle {\ begin {alineado} \ rho \ cos \ varphi & = \ sigma \ tau \\\ rho \ sin \ varphi & = {\ frac {1} {2}} \ left (\ tau ^ {2} - \ sigma ^ {2} \ right) \\ z & = z \ end {alineado}}}

Vectores de unidades parabólicas expresados ​​en términos de vectores de unidades cartesianas:

{\ displaystyle {\ begin {alineado} {\ boldsymbol {\ hat {\ sigma}}} & = {\ frac {\ tau {\ hat {\ mathbf {x}}} - \ sigma {\ hat {\ mathbf { y}}}} {\ sqrt {\ tau ^ {2} + \ sigma ^ {2}}}} \\ {\ boldsymbol {\ hat {\ tau}}} & = {\ frac {\ sigma {\ hat {\ mathbf {x}}} + \ tau {\ hat {\ mathbf {y}}}} {\ sqrt {\ tau ^ {2} + \ sigma ^ {2}}}} \\\ mathbf {\ hat {z}} & = \ mathbf {\ hat {z}} \ end {alineado}}}

Armónicos cilindro parabólicos [ editar ]

Dado que todas las superficies de la constante σ , τ y z son conicoides , la ecuación de Laplace se puede separar en coordenadas cilíndricas parabólicas. Usando la técnica de la separación de variables , se puede escribir una solución separada a la ecuación de Laplace:

$${\ displaystyle V = S (\ sigma) T (\ tau) Z (z)}

y la ecuación de Laplace, dividida por V , se escribe:

$${\ displaystyle {\ frac {1} {\ sigma ^ {2} + \ tau ^ {2}}} \ left [{\ frac {\ ddot {S}} {S}} + {\ frac {\ ddot { T}} {T}} \ right] + {\ frac {\ ddot {Z}} {Z}} = 0}

Ya que la ecuación Z está separada del resto, podemos escribir

$${\ displaystyle {\ frac {\ ddot {Z}} {Z}} = - m ^ {2}}

donde m es constante. Z ( z ) tiene la solución:

$${\ displaystyle Z_ {m} (z) = A_ {1} \, e ^ {imz} + A_ {2} \, e ^ {- imz}}

Sustituyendo - m ² por$${\ displaystyle {\ ddot {Z}} / Z}, La ecuación de Laplace se puede escribir ahora:

$${\ displaystyle \ left [{\ frac {\ ddot {S}} {S}} + {\ frac {\ ddot {T}} {T}} \ right] = m ^ {2} (\ sigma ^ {2 } + \ tau ^ {2})}

Ahora podemos separar las funciones S y T e introducir otra constante n ² para obtener:

$${\ displaystyle {\ ddot {S}} - (m ^ {2} \ sigma ^ {2} + n ^ {2}) S = 0}

$${\ displaystyle {\ ddot {T}} - (m ^ {2} \ tau ^ {2} -n ^ {2}) T = 0}

Las soluciones a estas ecuaciones son las funciones cilindricas parabólicas.

$${\ displaystyle S_ {mn} (\ sigma) = A_ {3} y_ {1} (n ^ {2} / 2m, \ sigma {\ sqrt {2m}}) + A_ {4} y_ {2} (n ^ {2} / 2m, \ sigma {\ sqrt {2m}})}

$${\ displaystyle T_ {mn} (\ tau) = A_ {5} y_ {1} (n ^ {2} / 2m, i \ tau {\ sqrt {2m}}) + A_ {6} y_ {2} ( n ^ {2} / 2m, i \ tau {\ sqrt {2m}})}

Los armónicos del cilindro parabólico para ( m , n ) son ahora el producto de las soluciones. La combinación reducirá el número de constantes y la solución general a la ecuación de Laplace se puede escribir:

$${\ displaystyle V (\ sigma, \ tau, z) = \ sum _ {m, n} A_ {mn} S_ {mn} T_ {mn} Z_ {m}}

Aplicaciones [ editar ]

Las aplicaciones clásicas de las coordenadas cilíndricas parabólicas están en la resolución de ecuaciones diferenciales parciales , por ejemplo, la ecuación de Laplace o la ecuación de Helmholtz , para las cuales tales coordenadas permiten una separación de variables . Un ejemplo típico sería el campo eléctrico que rodea una placa conductora semi-infinita plana.