SISTEMAS DE COORDENADAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Las tres superficies coordinadas de prolate sonferoidales. El esferoide prolado rojo (esfera estirada) corresponde a μ  = 1, y el hiperboloide azul de dos hojas corresponde a ν  = 45 °. El semiplano amarillo corresponde a φ  = −60 °, que se mide en relación con el eje x (resaltado en verde). La esfera negra representa el punto de intersección de las tres superficies, que tiene coordenadas cartesianas de aproximadamente (0.831, −1.439, 2.182).

Las coordenadas esferoidales de Prolate son un sistema de coordenadas ortogonales tridimensional que resulta de la rotación del sistema de coordenadas elíptico bidimensional alrededor del eje focal de la elipse, es decir, el eje de simetría en el que se encuentran los focos. La rotación sobre el otro eje produce coordenadas esferoidales oblatas . Las coordenadas esferoideas planas también se pueden considerar como un caso límite de coordenadas elipsoidales en las que los dos ejes principales más pequeños tienen la misma longitud.

Las coordenadas esferoidales de Prolate se pueden utilizar para resolver varias ecuaciones diferenciales parciales en las que las condiciones de los límites coinciden con su simetría y forma, como la resolución de un campo producido por dos centros, que se toman como los focos en el eje z . Un ejemplo es resolver la función de onda de un electrón que se mueve en el campo electromagnético de dos núcleos cargados positivamente , como en el ion molecular de hidrógeno , H ₂ ⁺ . Otro ejemplo es resolver el campo eléctricogenerado por dos puntas de electrodos pequeños . Otros casos limitantes incluyen áreas generadas por un segmento de línea (μ  = 0) o una línea con un segmento faltante (ν = 0).

Definición [ editar ]

Prolate las coordenadas esferoidales μ y ν para a  = 1. Las líneas de valores iguales de μ y ν se muestran en el plano xz , es decir, para φ  = 0. Las superficies de la constante μ y ν se obtienen por rotación alrededor del eje z , de modo que el diagrama sea válido para cualquier plano que contenga el eje z : es decir, para cualquier φ .

La definición más común de coordenadas esferoidales $${\ displaystyle (\ mu, \ nu, \ varphi)} es

$${\ displaystyle x = a \ sinh \ mu \ sin \ nu \ cos \ varphi}

$${\ displaystyle y = a \ sinh \ mu \ sin \ nu \ sin \ varphi}

$${\ displaystyle z = a \ cosh \ mu \ cos \ nu}

dónde $${\ displaystyle \ mu} es un número real no negativo y $${\ displaystyle \ nu \ en [0, \ pi]}. El ángulo azimutal$${\ displaystyle \ varphi} pertenece al intervalo $${\ displaystyle [0,2 \ pi]}.

La identidad trigonométrica.

$${\ displaystyle {\ frac {z ^ {2}} {a ^ {2} \ cosh ^ {2} \ mu}} + {\ frac {x ^ {2} + y ^ {2}} {a ^ { 2} \ sinh ^ {2} \ mu}} = \ cos ^ {2} \ nu + \ sin ^ {2} \ nu = 1}

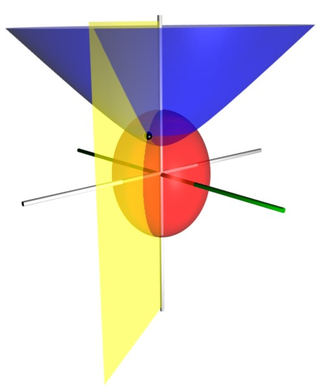
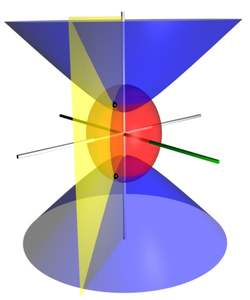
muestra que las superficies de constante $${\ displaystyle \ mu}Forman esferoides prolatos , ya que son elipsis giradas alrededor del eje que une sus focos. Del mismo modo, la identidad trigonométrica hiperbólica.

$${\ displaystyle {\ frac {z ^ {2}} {a ^ {2} \ cos ^ {2} \ nu}} - {\ frac {x ^ {2} + y ^ {2}} {a ^ { 2} \ sin ^ {2} \ nu}} = \ cosh ^ {2} \ mu - \ sinh ^ {2} \ mu = 1}

muestra que las superficies de constante $${\ displaystyle \ nu}Forman hiperboloides de revolución.

Las distancias desde los focos ubicados en $${\ displaystyle (x, y, z) = (0,0, \ pm a)} son

$${\ displaystyle r _ {\ pm} = {\ sqrt {x ^ {2} + y ^ {2} + (z \ mp a) ^ {2}}} = a (\ cosh \ mu \ mp \ cos \ nu ).

Factores de escala [ editar ]

Los factores de escala para las coordenadas elípticas. $${\ displaystyle (\ mu, \ nu)} son iguales

$${\ displaystyle h _ {\ mu} = h _ {\ nu} = a {\ sqrt {\ sinh ^ {2} \ mu + \ sin ^ {2} \ nu}}}

mientras que el factor de escala azimutal es igual

$${\ displaystyle h _ {\ varphi} = a \ sinh \ mu \ sin \ nu}

En consecuencia, un elemento de volumen infinitesimal es igual a

$${\ displaystyle dV = a ^ {3} \ sinh \ mu \ sin \ nu (\ sinh ^ {2} \ mu + \ sin ^ {2} \ nu) \, d \ mu \, d \ nu \, d \ varphi}

y el laplaciano se puede escribir

{\ displaystyle {\ begin {alineado} \ nabla ^ {2} \ Phi = {} & {\ frac {1} {a ^ {2} (\ sinh ^ {2} \ mu + \ sin ^ {2} \ nu)}} \ left [{\ frac {\ partial ^ {2} \ Phi} {\ partial \ mu ^ {2}}} + {\ frac {\ partial ^ {2} \ Phi} {\ partial \ nu ^ {2}}} + \ coth \ mu {\ frac {\ partial \ Phi} {\ partial \ mu}} + \ cot \ nu {\ frac {\ partial \ Phi} {\ partial \ nu}} \ right ] \\ [6pt] & {} + {\ frac {1} {a ^ {2} \ sinh ^ {2} \ mu \ sin ^ {2} \ nu}} {\ frac {\ partial ^ {2} \ Phi} {\ partial \ varphi ^ {2}}} \ end {alineado}}}

Otros operadores diferenciales tales como $${\ displaystyle \ nabla \ cdot \ mathbf {F}} y $${\ displaystyle \ nabla \ times \ mathbf {F}} Se puede expresar en las coordenadas. $${\ displaystyle (\ mu, \ nu, \ varphi)}sustituyendo los factores de escala en las fórmulas generales que se encuentran en las coordenadas ortogonales.

Definición alternativa [ editar ]

En principio, una definición de coordenadas esferoidales proladas podría ser degenerada. En otras palabras, un único conjunto de coordenadas podría corresponder a dos puntos en las coordenadas cartesianas ; Esto se ilustra aquí con dos esferas negras, una en cada hoja del hiperboloide y ubicadas en ( x , y , ± z ). Sin embargo, ninguna de las definiciones presentadas aquí son degeneradas.

Un conjunto alternativo y geométricamente intuitivo de coordenadas esferoidales proladas. $${\ displaystyle (\ sigma, \ tau, \ phi)} se utilizan a veces, donde $${\ displaystyle \ sigma = \ cosh \ mu} y $${\ displaystyle \ tau = \ cos \ nu}. De ahí, las curvas de constante.$${\ displaystyle \ sigma} Son esferoides prolatos, mientras que las curvas de constante. $${\ displaystyle \ tau}Son hiperboloides de revolución. La coordenada$${\ displaystyle \ tau} pertenece al intervalo [−1, 1], mientras que $${\ displaystyle \ sigma} la coordenada debe ser mayor o igual que uno.

Las coordenadas $${\ displaystyle \ sigma} y $${\ displaystyle \ tau} Tener una relación simple con las distancias a los focos. $${\ displaystyle F_ {1}} y $${\ displaystyle F_ {2}}. Para cualquier punto del plano, la suma. $${\ displaystyle d_ {1} + d_ {2}} De sus distancias a los focos iguales. $${\ displaystyle 2a \ sigma}, mientras que su diferencia $${\ displaystyle d_ {1} -d_ {2}} es igual a $${\ displaystyle 2a \ tau}. Por lo tanto, la distancia a$${\ displaystyle F_ {1}}es $${\ displaystyle a (\ sigma + \ tau)}, mientras que la distancia a $${\ displaystyle F_ {2}} es $${\ displaystyle a (\ sigma - \ tau)}. (Recordar que$${\ displaystyle F_ {1}} y $${\ displaystyle F_ {2}} se encuentran en $${\ displaystyle z = -a} y $${\ displaystyle z = + a}, respectivamente.) Esto da las siguientes expresiones para $${\ displaystyle \ sigma}, $${\ displaystyle \ tau}y $${\ displaystyle \ varphi}:

$${\ displaystyle \ sigma = {\ frac {1} {2a}} \ left ({\ sqrt {x ^ {2} + y ^ {2} + (z + a) ^ {2}}} + {\ sqrt {x ^ {2} + y ^ {2} + (za) ^ {2}}} \ derecha)}

$${\ displaystyle \ tau = {\ frac {1} {2a}} \ left ({\ sqrt {x ^ {2} + y ^ {2} + (z + a) ^ {2}}} - {\ sqrt {x ^ {2} + y ^ {2} + (za) ^ {2}}} \ derecha)}

$${\ displaystyle \ varphi = \ arctan \ left ({\ frac {y} {x}} \ right)}

A diferencia de las coordenadas esferoidales oblatas análogas , las coordenadas esferoides proladas (σ, τ, φ) no están degeneradas; En otras palabras, existe una correspondencia única y reversibleentre ellos y las coordenadas cartesianas.

$${\ displaystyle x = a {\ sqrt {(\ sigma ^ {2} -1) (1- \ tau ^ {2})}} \ cos \ varphi}

$${\ displaystyle y = a {\ sqrt {(\ sigma ^ {2} -1) (1- \ tau ^ {2})}} \ sin \ varphi}

$${\ displaystyle z = a \ \ sigma \ \ tau}

Factores de escala alternativos [ editar ]

Los factores de escala para las coordenadas elípticas alternativas. $${\ displaystyle (\ sigma, \ tau, \ varphi)} son

$${\ displaystyle h _ {\ sigma} = a {\ sqrt {\ frac {\ sigma ^ {2} - \ tau ^ {2}} {\ sigma ^ {2} -1}}}}

$${\ displaystyle h _ {\ tau} = a {\ sqrt {\ frac {\ sigma ^ {2} - \ tau ^ {2}} {1- \ tau ^ {2}}}}}

mientras que el factor de escala azimutal es ahora

$${\ displaystyle h _ {\ varphi} = a {\ sqrt {\ left (\ sigma ^ {2} -1 \ right) \ left (1- \ tau ^ {2} \ right)}}}

Por lo tanto, el elemento de volumen infinitesimal se convierte en

$${\ displaystyle dV = a ^ {3} (\ sigma ^ {2} - \ tau ^ {2}) \, d \ sigma \, d \ tau \, d \ varphi}

y los iguales laplacianos

{\ displaystyle {\ begin {alineado} \ nabla ^ {2} \ Phi = {} & {\ frac {1} {a ^ {2} (\ sigma ^ {2} - \ tau ^ {2})}} \ left \ {{\ frac {\ partial} {\ partial \ sigma}} \ left [\ left (\ sigma ^ {2} -1 \ right) {\ frac {\ partial \ Phi} {\ partial \ sigma} } \ right] + {\ frac {\ partial} {\ partial \ tau}} \ left [(1- \ tau ^ {2}) {\ frac {\ partial \ Phi} {\ partial \ tau}} \ right ] \ right \} \\ & {} + {\ frac {1} {a ^ {2} (\ sigma ^ {2} -1) (1- \ tau ^ {2})}} {\ frac {\ parcial ^ {2} \ Phi} {\ partial \ varphi ^ {2}}} \ end {alineado}}}

Otros operadores diferenciales tales como $${\ displaystyle \ nabla \ cdot \ mathbf {F}} y $${\ displaystyle \ nabla \ times \ mathbf {F}} Se puede expresar en las coordenadas. $${\ displaystyle (\ sigma, \ tau)}sustituyendo los factores de escala en las fórmulas generales que se encuentran en las coordenadas ortogonales.

Como en el caso de las coordenadas esféricas , la ecuación de Laplace puede resolverse mediante el método de separación de variables para obtener soluciones en forma de armónicos esferoidales prolados , que son convenientes de usar cuando las condiciones de contorno se definen en una superficie con una coordenada esferoidal constante prolate (Ver Smythe, 1968).

Las coordenadas Quadray , también conocidas como coordenadas tetray o coordenadas chakovianas , fueron inventadas por Darrel Jarmusch y desarrolladas aún más por David Chako, Tom Ace, Kirby Urner, y otros, como otra versión de coordenadas simples , un sistema de coordenadas que usa un simplex o un tetraedrocomo Su base es el poliedro. 

Definición geométrica [ editar ]

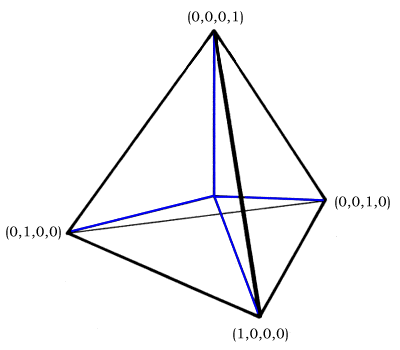
Los cuatro vectores básicos provienen del centro de un tetraedro regular y van a sus cuatro esquinas. Sus direcciones de coordenadas son (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0) y (0, 0, 0, 1) respectivamente. Estos pueden ser escalados y combinados linealmente para abarcar el espacio XYZ convencional , con al menos una de las cuatro coordenadas innecesarias (establecidas en cero) en cualquier cuadrante dado.

El esquema de normalización es algo inusual para mantener todas las coordenadas no negativas. Típico de los sistemas de coordenadas de este tipo (a, a, a, a) es un vector de identidad y se puede agregar para normalizar un resultado. Para negar (1,0,0,0), escriba (−1, 0, 0, 0) y luego agregue (1, 1, 1, 1) para obtener (0, 1, 1, 1).

Importancia pedagógica [ editar ]

Una aplicación típica podría establecer los bordes del tetraedro base como unidad, con los cuadrantes considerados como unidad en alguna otra escala. El tetraedro en sí también puede definirse como la unidad de volumen, aunque la infraestructura no exige este ajuste.

Los cuatro cuadrantes pueden combinarse linealmente para proporcionar coordenadas enteras para el tetraedro inverso (0,1,1,1), (1,0,1,1), (1,1,0,1), (1,1, 1,0), y para el cubo, octaedro, dodecaedro rombal y cuboctaedro de los volúmenes 3, 4, 6 y 20 respectivamente, dado el tetraedro de inicio del volumen unitario.

Por ejemplo, dados A, B, C, D como (1,0,0,0), (0,1,0,0), (0,0,1,0) y (0,0,0,1 ) respectivamente, los vértices de un octaedro con la misma longitud de borde y volumen cuatro serían A + B, A + C, A + D, B + C, B + D, C + D o las ocho permutaciones de {1,1 , 0,0}. Los vértices del volumen 20 cuboctaedro son 12 permutaciones de {2,1,1,0}.

Forma Volumen Inventario de vértices (suma de Quadrays) Tetraedro 1 A B C D Tetraedro Inverso 1 E, F, G, H = B + C + D, A + C + D, A + B + D, A + B + C Duo-Tet Cube 3 A a H Octaedro 4 I, J, K, L, M, N = A + B, A + C, A + D, B + C, B + D, C + D Dodecaedro rombal 6 De la A a la N Cuboctaedro 20 O, P, Q, R, S, T = I + J, I + K, I + L, I + M, N + J, N + K; U, V, W, X, Y, Z = N + L, N + M, J + L, L + M, M + K, K + J

Si uno ahora llama a este volumen "4D" como en "cuatro dimensiones" o "cuatro direccionales", hemos preparado la bomba para comprender la "geometría 4D" de R. Buckminster Fuller o sinergética .