MATEMÁTICAS ELEMENTALES

ÁLGEBRA ELEMENTAL - FRACCIONES

teorema de Midy , llamado así por el matemático francés E. Midy, ^[1] [2] es una declaración sobre la expansión decimal de las fracciones a / p, donde p es primo y a / p tiene una expansión decimalperiódica con un período par (secuencia A028416 en el OEIS ). Si el período de la representación decimal de a / p es 2 n , entonces

$${\ displaystyle {\ frac {a} {p}} = 0. {\ overline {a_ {1} a_ {2} a_ {3} \ dots a_ {n} a_ {n + 1} \ dots a_ {2n} }}}

luego los dígitos en la segunda mitad del período decimal que se repite son el complemento a 9 de los dígitos correspondientes en su primera mitad. En otras palabras,

$${\ displaystyle a_ {i} + a_ {i + n} = 9}

$${\ displaystyle a_ {1} \ dots a_ {n} + a_ {n + 1} \ dots a_ {2n} = 10 ^ {n} -1.}

Por ejemplo,

$${\ displaystyle {\ frac {1} {13}} = 0. {\ overline {076923}} {\ text {y}} 076 + 923 = 999.}

$${\ displaystyle {\ frac {1} {17}} = 0. {\ overline {0588235294117647}} {\ text {and}} 05882352 + 94117647 = 99999999.}

Extendió el teorema de Midy [ editar ]

Si k es cualquier divisor del período de la expansión decimal de a / p (donde p es nuevamente un número primo), entonces el teorema de Midy se puede generalizar de la siguiente manera. El teorema extendido de Midy ^[3]establece que si la parte que se repite de la expansión decimal de a / p se divide en números de k dígitos, entonces su suma es un múltiplo de 10 ^k  - 1.

Por ejemplo,

$${\ displaystyle {\ frac {1} {19}} = 0. {\ overline {052631578947368421}}

tiene un período de 18. Dividir la parte que se repite en números de 6 dígitos y sumarlos da

$${\ displaystyle 052631 + 578947 + 368421 = 999999.}

De manera similar, dividir la porción repetida en números de 3 dígitos y sumarlos da

$${\ displaystyle 052 + 631 + 578 + 947 + 368 + 421 = 2997 = 3 \ veces 999.}

El teorema de Midy en otras bases [ editar ]

El teorema de Midy y su extensión no dependen de las propiedades especiales de la expansión decimal, pero funcionan igual de bien en cualquier base b , siempre que reemplacemos 10 ^k  - 1 con b ^k  - 1 y realicemos la suma en la base b .

Por ejemplo, en octal.

{\ displaystyle {\ begin {alineado} & {\ frac {1} {19}} = 0. {\ overline {032745}} _ {8} \\ [8pt] & 032_ {8} + 745_ {8} = 777_ {8} \\ [8pt] & 03_ {8} + 27_ {8} + 45_ {8} = 77_ {8}. \ End {alineado}}}

En duodecimal (usando dos y tres invertidos para diez y once, respectivamente)

{\ displaystyle {\ begin {alineado} & {\ frac {1} {19}} = 0. {\ overline {076 {\ mathcal {E}} 45}} _ {12} \\ [8pt] & 076_ {12 } + {\ mathcal {E}} 45_ {12} = {\ mathcal {EEE}} _ {12} \\ [8pt] & 07_ {12} +6 {\ mathcal {E}} _ {12} + 45_ { 12} = {\ mathcal {EE}} _ {12} \ end {alineado}}}

Demostración del teorema de Midy [ editar ]

Se pueden dar pruebas cortas del teorema de Midy usando los resultados de la teoría de grupos . Sin embargo, también es posible probar el teorema de Midy usando álgebra elemental y aritmética modular :

Sea p primo y a / p sea ​​una fracción entre 0 y 1. Suponga que la expansión de a / p en la base b tiene un período de ℓ , entonces

{\ displaystyle {\ begin {alineado} & {\ frac {a} {p}} = [0. {\ overline {a_ {1} a_ {2} \ dots a _ {\ ell}}}] _ {b} \\ [6pt] & \ Rightarrow {\ frac {a} {p}} b ^ {\ ell} = [a_ {1} a_ {2} \ dots a _ {\ ell}. {\ Overline {a_ {1} a_ {2} \ dots a _ {\ ell}}}] _ {b} \\ [6pt] & \ Rightarrow {\ frac {a} {p}} b ^ {\ ell} = N + [0. {\ overline {a_ {1} a_ {2} \ dots a _ {\ ell}}}] _ {b} = N + {\ frac {a} {p}} \\ [6pt] & \ Rightarrow {\ frac {a} { p}} = {\ frac {N} {b ^ {\ ell} -1}} \ end {alineado}}}

donde N es el número entero cuya expansión en base b es la cadena a ₁ a ₂ ... a _ℓ .

Tenga en cuenta que b ^ℓ  - 1 es un múltiplo de p porque ( b ^ℓ  - 1) a / p es un número entero. Además, b ⁿ −1 noes un múltiplo de p para cualquier valor de n menor que ℓ , porque de lo contrario el período de repetición de a / pen la base b sería menor que ℓ .   

Ahora supongamos que ℓ  =  hk . Entonces b ^ℓ  - 1 es un múltiplo de b ^k  - 1. (Para ver esto, sustituya x por b ^k ; entonces b ^ℓ  =  x ^h y x  - 1 es un factor de x ^h  - 1). Diga b ^ℓ  - 1 =  m ( b ^k  - 1), entonces   

$${\ displaystyle {\ frac {a} {p}} = {\ frac {N} {m (b ^ {k} -1)}}.

Pero b ^ℓ  - 1 es un múltiplo de p ; b ^k  - 1 no es un múltiplo de p (porque k es menor que ℓ  ); y p es un primo; así que m debe ser un múltiplo de p y  

$${\ displaystyle {\ frac {am} {p}} = {\ frac {N} {b ^ {k} -1}}}

es un entero En otras palabras,

$${\ displaystyle N \ equiv 0 {\ pmod {b ^ {k} -1}}.}

Ahora divida la cadena a ₁ a ₂ ... a _ℓ en h partes iguales de longitud k , y deje que estos representen los números enteros N ₀ ... N _{h  - 1} en la base b , de modo que

{\ displaystyle {\ begin {alineado} N_ {h-1} & = [a_ {1} \ dots a_ {k}] _ {b} \\ N_ {h-2} & = [a_ {k + 1} \ dots a_ {2k}] _ {b} \\ & {} \ \ \ vdots \\ N_ {0} & = [a_ {l-k + 1} \ dots a_ {l}] _ {b} \ end {alineado}}}

Para probar el teorema extendido de Midy en la base b , debemos demostrar que la suma de los enteros h N _i es un múltiplo de b ^k  - 1.

Como b ^k es congruente con 1 módulo b ^k  - 1, cualquier potencia de b ^k también será congruente con 1 módulo b ^k  - 1.

$${\ displaystyle N = \ sum _ {i = 0} ^ {h-1} N_ {i} b ^ {ik} = \ sum _ {i = 0} ^ {h-1} N_ {i} (b ^ {k}) ^ {i}}

$${\ displaystyle \ Rightarrow N \ equiv \ sum _ {i = 0} ^ {h-1} N_ {i} {\ pmod {b ^ {k} -1}}}

$${\ displaystyle \ Rightarrow \ sum _ {i = 0} ^ {h-1} N_ {i} \ equiv 0 {\ pmod {b ^ {k} -1}}}

lo que demuestra el teorema extendido de Midy en la base b .

Para probar el teorema de Midy original, tome el caso especial donde h = 2. Tenga en cuenta que N ₀ y N ₁ están representados por cadenas de k dígitos en la base b para que ambos cumplan

$${\ displaystyle 0 \ leq N_ {i} \ leq b ^ {k} -1.}

N ₀ y N ₁ no pueden ser iguales a 0 (de lo contrario a / p = 0) y no pueden ser iguales a b ^k  - 1 (de lo contrario a / p = 1), entonces

{\ displaystyle 0

y como N ₀  +  N ₁ es un múltiplo de b ^k  - 1, se deduce que

$${\ displaystyle N_ {0} + N_ {1} = b ^ {k} -1.}

Corolario [ editar ]

De lo anterior,

$${\ displaystyle {\ frac {am} {p}}} es un número entero

Así $${\ displaystyle m \ equiv 0 {\ pmod {p}}}

Y así por $${\ displaystyle k = {\ frac {l} {2}}}

$${\ displaystyle b ^ {\ frac {l} {2}} + 1 \ equiv 0 (\ pmod {p}}}

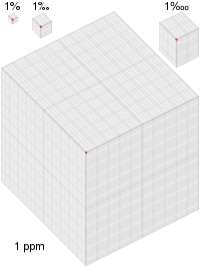
por $${\ displaystyle k = {\ frac {l} {3}}} y es un entero

$${\ displaystyle b ^ {{\ frac {2} {3}} l} + b ^ {\ frac {l} {3}} + 1 \ equiv 0 (\ pmod {p}}}

y así.

 millonésima es igual a 0.000 001, o 1 x 10 ⁻⁶ en notación científica . Es el recíproco de un millón , y también puede escribirse como 1/1 000 000. ^{[1] Las} unidades que usan esta fracción pueden indicarse usando el prefijo "micro-" del griego , que significa "pequeño". ^{[2] Los} números de esta cantidad se expresan en términos de µ (la letra griega mu ). ^[3]

"Millionth" también puede significar el número ordinal que viene después de los novecientos noventa y nueve mil novecientos noventa y nueve y antes del millón y primero. 

Por meg es igual a 0.001 permil o 0.0001 por ciento o partes por millón de ppm . La unidad se utiliza típicamente en análisis de isótopos multiplicando una relación de isótopo en la anotación delta, por ejemplo δ ¹⁸ O , por 1000000. ^[1] [2] Esta anotación se usa típicamente en estudios de gases traza atmosféricos, donde se necesita una alta precisión Para una interpretación significativa de los resultados.

 porcentaje es un número o razón expresada como una fracción de 100. A menudo se denota con el signo de porcentaje , "%", o las abreviaturas "pct.", "Pct"; a veces también se usa la abreviatura "pc". ^[1] Un porcentaje es un número adimensional (número puro).

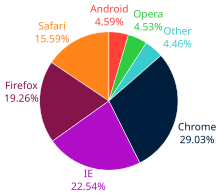
Un gráfico circular que muestra el porcentaje por navegador web que visita los sitios de Wikimedia (abril de 2009 a 2012)

Ejemplos

Por ejemplo, 45% (leer como "cuarenta y cinco por ciento") es igual a 45/100 , 45: 100 , o 0,45 . Los porcentajes se utilizan a menudo para expresar una parte proporcional de un total.

(De manera similar, uno puede expresar un número como una fracción de 1,000 usando el término " por mil " o el símbolo " ‰ ".)

Ejemplo 1

Si el 50% del número total de estudiantes en la clase son hombres, eso significa que 50 de cada 100 estudiantes son hombres. Si hay 500 estudiantes, entonces 250 de ellos son hombres.

Ejemplo 2

Un aumento de $ 0.15 sobre un precio de $ 2.50 es un aumento de una fracción de 0.15/2.50 = 0.06. Expresado como un porcentaje, esto es un aumento del 6%.

Si bien muchos valores porcentuales están entre 0 y 100, no hay restricción matemática y los porcentajes pueden asumir otros valores. ^[2] Por ejemplo, es común referirse a 111% o −35%, especialmente para cambios porcentuales y comparaciones.

Historia

En Roma antigua , mucho antes de la existencia del sistema decimal, los cálculos se hacen a menudo en las fracciones que eran múltiplos de 1/100 . Por ejemplo, Augusto estableció un impuesto de 1/100 en los productos vendidos en una subasta conocida como centesima rerum venalium . El cálculo con estas fracciones fue equivalente a calcular los porcentajes. A medida que las denominaciones de dinero crecieron en la Edad Media , los cálculos con un denominador de 100 se hicieron más estándar y, desde finales del siglo XV hasta principios del siglo XVI, se hizo común que los textos aritméticos incluyeran tales cálculos. Muchos de estos textos aplicaron estos métodos a las pérdidas y ganancias, a las tasas de interés y alRegla de tres . En el siglo XVII, era normal citar las tasas de interés en centésimas. ^[3]

Signo de porcentaje

Artículo principal: Signo de porcentaje

Un signo de porcentaje

El término "porcentaje" se deriva del latín por ciento , que significa "por cien". ^[4] El signo de "porcentaje" evolucionó mediante la contracción gradual del término italiano por cento , que significa "por cien". El "per" se abrevió a menudo como "p". Y finalmente desapareció por completo. El "cento" se contrajo a dos círculos separados por una línea horizontal, de la cual se deriva el símbolo moderno "%". ^[5]

Cálculos

El valor porcentual se calcula multiplicando el valor numérico de la relación por 100. Por ejemplo, para encontrar 50 manzanas como un porcentaje de 1250 manzanas, primero calcular la relación de 50/1.250 = 0,04, y luego se multiplica por 100 para obtener 4%. El valor porcentual también se puede encontrar al multiplicar primero, por lo que en este ejemplo, los 50 se multiplicarían por 100 para obtener 5,000, y este resultado se dividiría entre 1250 para dar un 4%.

Para calcular un porcentaje de un porcentaje, convierta ambos porcentajes a fracciones de 100, o decimales, y multiplíquelos. Por ejemplo, el 50% del 40% es:

50/100 ×40/100 = 0,50 × 0,40 = 0,20 =20/100 = 20%.

No es correcto dividir por 100 y usar el signo de porcentaje al mismo tiempo. (Por ejemplo, 25% = 25/100 = 0,25 , no 25%/100 , que en realidad es ²⁵/₁₀₀/100 = 0,0025 . Un término tal como 100/100 % también sería incorrecto, esto se lee como 1 por ciento, incluso Si la intención era decir 100%. 

Cuando hablamos de un porcentaje, es importante especificar a qué se refiere, es decir, cuál es el total que corresponde al 100%. El siguiente problema ilustra este punto.

En una determinada universidad, el 60% de todos los estudiantes son mujeres, y el 10% de todos los estudiantes son estudiantes de ciencias de la computación. Si el 5% de las estudiantes son estudiantes de ciencias de la computación, ¿qué porcentaje de estudiantes de ciencias de la computación son mujeres?

Se nos pide que calculemos la proporción de estudiantes de ciencias de la computación para todas las carreras de ciencias de la computación. Sabemos que el 60% de todos los estudiantes son mujeres, y entre estos 5% son mayores de informática, por lo que se concluye que 60/100 × 5/100 = 3/100 o el 3% de todos los estudiantes son mayores de informática femeninos. Dividiéndolo por el 10% de todos los estudiantes que son mayores de informática, se llega a la respuesta: 3%/10% = 30/100 o el 30% de todas las carreras de ciencias de la computación son mujeres.

Este ejemplo está estrechamente relacionado con el concepto de probabilidad condicional .

Porcentaje de aumento y disminución.

Debido al uso inconsistente, no siempre queda claro en el contexto a qué se refiere un porcentaje. Cuando se habla de un "aumento del 10%" o una "caída del 10%" en una cantidad, la interpretación habitual es que esto es relativo al valor inicial de esa cantidad. Por ejemplo, si un artículo tiene un precio inicial de $ 200 y el precio sube un 10% (un aumento de $ 20), el nuevo precio será de $ 220. Tenga en cuenta que este precio final es el 110% del precio inicial (100% + 10% = 110%).

Algunos otros ejemplos de cambios porcentuales :

• Un aumento del 100% en una cantidad significa que la cantidad final es el 200% de la cantidad inicial (100% de la inicial + 100% de aumento = 200% de la inicial); en otras palabras, la cantidad se ha duplicado.
• Un aumento del 800% significa que la cantidad final es 9 veces la original (100% + 800% = 900% = 9 veces más grande).
• Una disminución del 60% significa que la cantidad final es del 40% del original (100% - 60% = 40%).
• Una disminución del 100% significa que la cantidad final es cero (100% - 100% = 0%).

En general, un cambio de x por ciento en una cantidad resulta en una cantidad final que es 100 +  x por ciento de la cantidad original (equivalentemente, (1 + 0.01 x ) veces la cantidad original).

Porcentajes compuestos

Los cambios porcentuales aplicados secuencialmente no se suman de la manera habitual. Por ejemplo, si el aumento del 10% en el precio considerado anteriormente (en el artículo de $ 200, aumentando su precio a $ 220) es seguido por una disminución del 10% en el precio (una disminución de $ 22), el precio final será de $ 198, noel precio final. Precio original de $ 200. La razón de la aparente discrepancia es que los cambios de dos por ciento (+ 10% y −10%) se miden en relación con diferentes cantidades ($ 200 y $ 220, respectivamente), y por lo tanto no se "cancelan".

En general, si un aumento del x por ciento es seguido por una disminución del x por ciento, y la cantidad inicial fue p , la cantidad final es p (1 + 0.01 x ) (1 - 0.01 x ) = p (1 - (0.01 x ) ² ) ; por lo tanto, el cambio neto es una disminución general en x por ciento de x por ciento (el cuadrado del por ciento de cambio original cuando se expresa como un número decimal). Así, en el ejemplo anterior, después de un aumento y disminución de x = 10 por ciento, la cantidad final, $ 198, fue del 10% del 10%, o 1%, menos que la cantidad inicial de $ 200. El cambio neto es el mismo para una disminución del x por ciento seguido por un aumento del x por ciento; la cantidad final es p (1 - 0.01 x ) (1 + 0.01 x ) = p (1 - (0.01 x ) ² ) .

Esto se puede ampliar para un caso en el que no tenga el mismo cambio porcentual. Si el cambio porcentual inicial es x y el segundo cambio porcentual es y , y la cantidad inicial fue p , entonces la cantidad final es p (1 + 0.01 x ) (1 + 0.01 y ) . Para cambiar el ejemplo anterior, después de un aumento de x = 10 por ciento y una disminución de y = −5 por ciento , la cantidad final, $ 209, es 4.5% más que la cantidad inicial de $ 200.

Como se muestra arriba, los cambios porcentuales se pueden aplicar en cualquier orden y tienen el mismo efecto.

En el caso de las tasas de interés , una forma muy común pero ambigua de decir que una tasa de interés aumentó del 10% anual al 15% anual, por ejemplo, es decir que la tasa de interés aumentó un 5%, lo que teóricamente podría significar que aumentó del 10% anual al 10,05% anual. Es más claro decir que la tasa de interés aumentó en 5 puntos porcentuales(páginas). La misma confusión entre los diferentes conceptos de porcentaje (edad) y puntos porcentuales puede causar un malentendido cuando los periodistas informan sobre los resultados de las elecciones, por ejemplo, expresando tanto los nuevos resultados como las diferencias con los resultados anteriores como porcentajes. Por ejemplo, si un partido obtiene el 41% de los votos y se dice que esto es un aumento del 2.5%, ¿significa que el resultado anterior fue del 40% (ya que 41 = 40 × (1 + 2.5/100 ) ) o del 38.5% ( ya que 41 = 38.5 + 2.5 )?

En los mercados financieros, es común referirse a un aumento de un punto porcentual (por ejemplo, del 3% anual al 4% anual) como un aumento de "100 puntos básicos".

Palabra y simbolo

Artículo principal: Signo de porcentaje

En inglés británico , el porcentaje se escribe generalmente como dos palabras ( porcentaje ), aunque el porcentaje y el percentil se escriben como una palabra. ^[6] En inglés americano , el porcentaje es la variante más común ^[7] (pero por milés se escribe como dos palabras).

A principios del siglo XX, había una abreviatura de puntos " por ciento ", en lugar de " por ciento ". La forma " por ciento " todavía se usa en el lenguaje altamente formal que se encuentra en ciertos documentos, como los acuerdos de préstamos comerciales (particularmente aquellos sujetos a, o inspirados por, el derecho común), así como en las transcripciones de Hansard de los procedimientos parlamentarios británicos. El término ha sido atribuido al latín por ciento . ^[8] El concepto de considerar los valores como partes de un centenar es originalmente griego . El símbolo de porcentaje (%) evolucionó a partir de un símbolo que abrevia el italiano por cento. En algunos otros idiomas, la forma procent o prosent se utiliza en su lugar. Algunos idiomas usan tanto una palabra derivada de porcentaje como una expresión en ese idioma que significa lo mismo, por ejemplo, rumian procent y la sută (por lo tanto, el 10% se puede leer o, a veces, escribir diez por [cada] cien , de manera similar con el inglés one out de diez ). Otras abreviaturas son más raras, pero a veces se ven.

Las guías de gramática y estilo a menudo difieren en cuanto a cómo se deben escribir los porcentajes. Por ejemplo, comúnmente se sugiere que la palabra porcentaje (o porcentaje) esté escrita en todos los textos, como en "1 por ciento" y no en "1%". Otras guías prefieren que la palabra se escriba en textos humanísticos, pero el símbolo se use en textos científicos. La mayoría de los guías aceptan que siempre se escriban con un número, como en "5 por ciento" y no en "cinco por ciento", siendo la única excepción al comienzo de una oración: "El diez por ciento de todos los escritores aman las guías de estilo". Los decimales son también para ser utilizados en lugar de fracciones, como en "3,5 por ciento de la ganancia" y no " 3 ¹ / ₂  por ciento de la ganancia". ¹ / ₂ sin garantía de préstamos% de 2032 Serie 2" . (Cuando las tasas de interés son muy bajos, el número 0 se incluye si el tipo de interés es inferior al 1%, por ejemplo, ' 0 ³ / ₄  % acciones propias', no " ³ ⁄ ₄ % de acciones en tesorería ".) También se acepta ampliamente el uso del símbolo de porcentaje (%) en material gráfico y gráfico.

De acuerdo con la práctica común del inglés, las guías de estilo, como el Manual de estilo de Chicago,generalmente indican que el número y el signo de porcentaje están escritos sin ningún espacio entre ellos. ^[9] Sin embargo, el Sistema Internacional de Unidades y la norma ISO 31-0 requieren un espacio. ^[10] [11]

Otros usos

La palabra "porcentaje" es a menudo un nombre inapropiado en el contexto de las estadísticas deportivas, cuando el número de referencia se expresa como un porcentaje decimal, no un porcentaje: "Los Phoenix Suns ' Shaquille O'Neal lideró la NBA con un .609 porcentaje de tiros de campo (FG%) durante la temporada 2008-09. " (O'Neal realizó el 60.9% de sus tiros, no el 0.609%.) Del mismo modo, el porcentaje de victorias de un equipo, la fracción de partidos que el club ha ganado, también se suele expresar como una proporción decimal; un equipo que tiene un porcentaje de victorias de .500 ha ganado el 50% de sus partidos. La práctica probablemente está relacionada con la manera similar en que se citan los promedios de bateo .

Como "porcentaje" se usa para describir la inclinación de la pendiente de una carretera o ferrocarril , cuya fórmula es 100 ×  subida/carrera que también podría expresarse como la tangente del ángulo de inclinación de 100. Esta es la relación de las distancias que un vehículo avanzaría vertical y horizontalmente, respectivamente, al subir o bajar, expresadas en porcentaje.

El porcentaje también se usa para expresar la composición de una mezcla por porcentaje en masa y por ciento en moles .

Unidades relacionadas

Visualización de 1%, 1 ‰, 1 ‱ y 1 ppm como la fracción del cubo rojo a su bloque respectivo (versión más grande)

• Punto porcentual
• Por mil (‰) 1 parte en 1,000
• Punto base () 1 parte en 10,000
• Por ciento mille (pcm) 1 parte en 100,000
• Partes por notación
• Grado (pendiente)
• Sistema por unidad