SISTEMAS DE COORDENADAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Coordinar las superficies de las coordenadas cilíndricas bipolares. La media luna amarilla corresponde a σ, mientras que el tubo rojo corresponde a τ y el plano azul corresponde a z = 1. Las tres superficies se intersecan en el punto P (se muestra como una esfera negra).

Las coordenadas cilíndricas bipolares son un sistema de coordenadas ortogonal tridimensional que resulta de proyectar el sistema de coordenadas bipolar bidimensional en el perpendicular$${\ displaystyle z}-dirección. Las dos lineas de focos $${\ displaystyle F_ {1}} y $${\ displaystyle F_ {2}}de los círculos apollonios proyectados generalmente se consideran definidos por$${\ displaystyle x = -a} y $${\ displaystyle x = + a}, respectivamente, (y por $${\ displaystyle y = 0}) en el sistema de coordenadas cartesiano .

El término "bipolar" se usa a menudo para describir otras curvas que tienen dos puntos singulares (focos), como elipsis , hipérbolas y óvalos de Cassini . Sin embargo, el término coordenadas bipolares nunca se usa para describir coordenadas asociadas con esas curvas, por ejemplo, coordenadas elípticas .

Definición básica [ editar ]

La definición más común de coordenadas cilíndricas bipolares. $${\ displaystyle (\ sigma, \ tau, z)} es

$${\ displaystyle x = a \ {\ frac {\ sinh \ tau} {\ cosh \ tau - \ cos \ sigma}}}

$${\ displaystyle y = a \ {\ frac {\ sin \ sigma} {\ cosh \ tau - \ cos \ sigma}}}

$${\ displaystyle z = \ z}

donde el $${\ displaystyle \ sigma} coordenada de un punto $${\ displaystyle P} es igual al ángulo $${\ displaystyle F_ {1} PF_ {2}} y el $${\ displaystyle \ tau}coordenada es igual al logaritmo naturalde la relación de las distancias$${\ displaystyle d_ {1}} y $${\ displaystyle d_ {2}} a las lineas focales

$${\ displaystyle \ tau = \ ln {\ frac {d_ {1}} {d_ {2}}}}

(Recordemos que las líneas focales $${\ displaystyle F_ {1}} y $${\ displaystyle F_ {2}} se encuentran en $${\ displaystyle x = -a} y $${\ displaystyle x = + a}, respectivamente.)

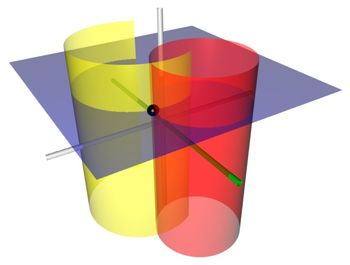
Superficies de constante. $${\ displaystyle \ sigma} Corresponden a cilindros de diferentes radios.

$${\ displaystyle x ^ {2} + \ left (ya \ cot \ sigma \ right) ^ {2} = {\ frac {a ^ {2}} {\ sin ^ {2} \ sigma}}}

Que todos pasen por las líneas focales y no sean concéntricos. Las superficies de constante.$${\ displaystyle \ tau} Son cilindros no intersecantes de diferentes radios.

$${\ displaystyle y ^ {2} + \ left (xa \ coth \ tau \ right) ^ {2} = {\ frac {a ^ {2}} {\ sinh ^ {2} \ tau}}}

Que rodean las líneas focales pero de nuevo no son concéntricas. Las líneas focales y todos estos cilindros son paralelos a los$${\ displaystyle z}-axis (la dirección de proyección). En el$${\ displaystyle z = 0} plano, los centros de la constante$${\ displaystyle \ sigma} y constante-$${\ displaystyle \ tau}cilindros se encuentran en el $${\ displaystyle y} y $${\ displaystyle x} Ejes, respectivamente.

Factores de escala [ editar ]

Los factores de escala para las coordenadas bipolares. $${\ displaystyle \ sigma} y $${\ displaystyle \ tau} son iguales

$${\ displaystyle h _ {\ sigma} = h _ {\ tau} = {\ frac {a} {\ cosh \ tau - \ cos \ sigma}}}

mientras que el factor de escala restante $${\ displaystyle h_ {z} = 1}. Así, el elemento de volumen infinitesimal es igual a

$${\ displaystyle dV = {\ frac {a ^ {2}} {\ left (\ cosh \ tau - \ cos \ sigma \ right) ^ {2}}} d \ sigma d \ tau dz}

y el laplaciano está dado por

$${\ displaystyle \ nabla ^ {2} \ Phi = {\ frac {1} {a ^ {2}}} \ left (\ cosh \ tau - \ cos \ sigma \ right) ^ {2} \ left ({\ frac {\ parcial ^ {2} \ Phi} {\ parcial \ sigma ^ {2}}} + {\ frac {\ parcial ^ {2} \ Phi} {\ parcial \ tau ^ {2}}} \ derecha) + {\ frac {\ parcial ^ {2} \ Phi} {\ parcial z ^ {2}}}}

Otros operadores diferenciales tales como $${\ displaystyle \ nabla \ cdot \ mathbf {F}} y $${\ displaystyle \ nabla \ times \ mathbf {F}} Se puede expresar en las coordenadas. $${\ displaystyle (\ sigma, \ tau)}sustituyendo los factores de escala en las fórmulas generales que se encuentran en las coordenadas ortogonales.

Aplicaciones [ editar ]

Las aplicaciones clásicas de las coordenadas bipolares están en la resolución de ecuaciones diferenciales parciales , por ejemplo, la ecuación de Laplace o la ecuación de Helmholtz , para las cuales las coordenadas bipolares permiten una separación de variables (en 2D). Un ejemplo típico sería el campo eléctrico que rodea dos conductores cilíndricos paralelos.

El espacio Blau consiste en el sistema de coordenadas multidimensional , creado al considerar el conjunto de variables sociodemográficas como dimensiones. Todas las características sociodemográficas son elementos potenciales del espacio Blau, incluidas características continuas como la edad, los años de educación, los ingresos, el prestigio ocupacional, la ubicación geográfica, etc. Además, las medidas categóricas de las características sociodemográficas, como la raza, el sexo, la religión, el lugar de nacimiento y otras, son dimensiones Blau. "Espacio Blau" es una construcción teórica que fue desarrollada por Miller McPherson y que lleva el nombre de Peter Blau . Más tarde fue elaborado por McPherson y Ranger-Moore. ^[1] [2]

La fuerza organizadora en el espacio Blau es el principio de homofilia , que sostiene que el flujo de informaciónde persona a persona es una función decreciente de la distancia en el espacio Blau. Las personas ubicadas a gran distancia en el espacio Blau tienen pocas probabilidades de interactuar, lo que crea las condiciones para las diferencias sociales en cualquier característica que se transmite a través de la comunicación social . El principio de homofilia localiza así la comunicación en el espacio Blau, lo que lleva al desarrollo de nichos sociales para la actividad humana y la organización social .

Aunque la idea de Blau Space se desarrolló originalmente para considerar a los individuos, se extendió al contexto de las ciudades (y otras unidades urbanas) en "Building a Blauürban Space" de Neal. 

 coordenadas canónicasson conjuntos de coordenadas en el espacio de fase que se pueden usar para describir un sistema físico en cualquier momento dado. Las coordenadas canónicas se utilizan en la formulación hamiltoniana de la mecánica clásica . Un concepto estrechamente relacionado también aparece en la mecánica cuántica ; vea el teorema de Stone-von Neumann y las relaciones de conmutación canónicas para más detalles.

Como la mecánica hamiltoniana se generaliza mediante geometría simpléctica y las transformaciones canónicas se generalizan mediante transformaciones de contacto , la definición de coordenadas canónicas del siglo XIX en la mecánica clásica se puede generalizar a una definición más abstracta de coordenadas del siglo XX en el conjunto cotangente de una variedad (la matemática noción de espacio de fase).

Definición en la mecánica clásica [ editar ]

En mecánica clásica , las coordenadas canónicas son coordenadas.$${\ displaystyle q_ {i}} y $${\ displaystyle p_ {i}}En el espacio de fase que se utilizan en el formalismo hamiltoniano . Las coordenadas canónicas satisfacen las relaciones de corchete de Poissonfundamentales :

$${\ displaystyle \ {q_ {i}, q_ {j} \} = 0 \ qquad \ {p_ {i}, p_ {j} \} = 0 \ qquad \ {q_ {i}, p_ {j} \} = \ delta _ {ij}}

Un ejemplo típico de coordenadas canónicas es para $${\ displaystyle q_ {i}}ser las coordenadas cartesianas habituales , y$${\ displaystyle p_ {i}}Ser los componentes del impulso . De ahí que, en general, la$${\ displaystyle p_ {i}} Las coordenadas se conocen como "momenta conjugada".

Las coordenadas canónicas se pueden obtener a partir de las coordenadas generalizadas del formalismo lagrangiano mediante una transformación de Legendre , o de otro conjunto de coordenadas canónicas mediante una transformación canónica .

Definición en paquetes cotangentes [ editar ]

Las coordenadas canónicas se definen como un conjunto especial de coordenadas en el paquete cotangente de un colector . Por lo general se escriben como un conjunto de$${\ displaystyle (q ^ {i}, p_ {j})} o $${\ displaystyle (x ^ {i}, p_ {j})}con las x o q denota las coordenadas en el colector subyacente y las p denotan el momento conjugado , que son formas 1 en el paquete cotangente en el punto q en el colector.

Una definición común de coordenadas canónicas es cualquier conjunto de coordenadas en el paquete cotangente que permite que la forma canónica se escriba en la forma

$${\ displaystyle \ sum _ {i} p_ {i} \, \ mathrm {d} q ^ {i}}

Hasta un diferencial total. Un cambio de coordenadas que conserva esta forma es una transformación canónica ; estos son un caso especial de simlectomorfismo , que son esencialmente un cambio de coordenadas en una variedad simpléctica .

En la siguiente exposición, asumimos que las variedades son variedades reales, de modo que los vectores cotangentes que actúan sobre vectores tangentes producen números reales.

Desarrollo formal [ editar ]

Dada una variedad Q , un campo vectorial X en Q (una sección del haz tangente TQ ) puede considerarse como una función que actúa sobre el haz cotangente , por la dualidad entre los espacios tangente y cotangente. Es decir, definir una función.

$${\ displaystyle P_ {X}: T ^ {*} Q \ a \ mathbb {R}}

tal que

$${\ displaystyle P_ {X} (q, p) = p (X_ {q})}

se mantiene para todos los vectores cotangentes p en$${\ displaystyle T_ {q} ^ {*} Q}. Aquí,$${\ displaystyle X_ {q}} es un vector en $${\ displaystyle T_ {q} Q}, el espacio tangente a la variedad Q en el punto q . La función$${\ displaystyle P_ {X}}se llama la función de impulso que corresponde a X .

En las coordenadas locales , el campo vectorial X en el punto q puede escribirse como

$${\ displaystyle X_ {q} = \ sum _ {i} X ^ {i} (q) {\ frac {\ parcial} {\ parcial q ^ {i}}}}

donde el $${\ displaystyle \ partial / \ partial q ^ {i}}son el marco de coordenadas en TQ . El momento conjugado tiene entonces la expresión

$${\ displaystyle P_ {X} (q, p) = \ sum _ {i} X ^ {i} (q) \; p_ {i}}

donde el $${\ displaystyle p_ {i}} Se definen como las funciones de momento correspondientes a los vectores. $${\ displaystyle \ partial / \ partial q ^ {i}}:

$${\ displaystyle p_ {i} = P _ {\ partial / \ partial q ^ {i}}}

los $${\ displaystyle q ^ {i}} junto con la $${\ displaystyle p_ {j}} juntos forman un sistema de coordenadas en el paquete cotangente $${\ displaystyle T ^ {*} Q}; estas coordenadas se llaman las coordenadas canónicas .

Coordenadas generalizadas [ editar ]

En la mecánica lagrangiana , se utiliza un conjunto diferente de coordenadas, denominadas coordenadas generalizadas . Estos son comúnmente denotados como$${\ displaystyle (q_ {i}, {\ dot {q}} _ {i})} con $${\ displaystyle q_ {i}}llamada la posición generalizada y$${\ displaystyle {\ dot {q}} _ {i}}La velocidad generalizada . Cuando se define un hamiltoniano en el paquete cotangente, entonces las coordenadas generalizadas se relacionan con las coordenadas canónicas por medio de las ecuaciones de Hamilton-Jacobi .