SISTEMAS DE COORDENADAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

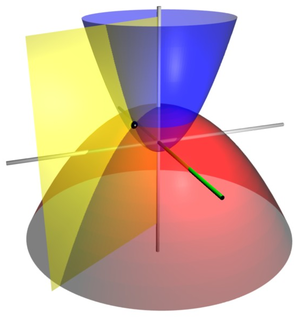
Las coordenadas paraboloides son un sistema de coordenadas ortogonal tridimensional $${\ displaystyle (\ lambda, \ mu, \ nu)}Eso generaliza el sistema de coordenadas parabólico bidimensional . Al igual que las coordenadas elipsoidalesrelacionadas , el sistema de coordenadas paraboloidales tiene superficies de coordenadas cuadráticas ortogonales que no se producen al girar o proyectar cualquier sistema de coordenadas ortogonales bidimensional.

Coordinar las superficies de las coordenadas paraboloidales tridimensionales.

Fórmulas básicas [ editar ]

Las coordenadas cartesianas. $${\ displaystyle (x, y, z)} Se puede producir a partir de las coordenadas elipsoidales. $${\ displaystyle (\ lambda, \ mu, \ nu)} por las ecuaciones

$${\ displaystyle x ^ {2} = {\ frac {\ left (A- \ lambda \ right) \ left (A- \ mu \ right) \ left (A- \ nu \ right)} {BA}}}

$${\ displaystyle y ^ {2} = {\ frac {\ left (B- \ lambda \ right) \ left (B- \ mu \ right) \ left (B- \ nu \ right)} {AB}}}

$${\ displaystyle z = {\ frac {1} {2}} \ left (A + B- \ lambda - \ mu - \ nu \ right)}

donde se aplican los siguientes límites a las coordenadas

{\ displaystyle \ lambda

Consecuentemente, superficies de constante. $${\ displaystyle \ lambda}son paraboloides elípticos

$${\ displaystyle {\ frac {x ^ {2}} {\ lambda -A}} + {\ frac {y ^ {2}} {\ lambda -B}} = 2z + \ lambda}

y superficies de constante $${\ displaystyle \ nu} son igualmente

$${\ displaystyle {\ frac {x ^ {2}} {\ nu -A}} + {\ frac {y ^ {2}} {\ nu -B}} = 2z + \ nu}

mientras que las superficies de constante $${\ displaystyle \ mu}son paraboloides hiperbólicos

$${\ displaystyle {\ frac {x ^ {2}} {\ mu -A}} + {\ frac {y ^ {2}} {\ mu -B}} = 2z + \ mu}

Factores de escala [ editar ]

Los factores de escala para las coordenadas paraboloides. $${\ displaystyle (\ lambda, \ mu, \ nu)} son

$${\ displaystyle h _ {\ lambda} = {\ frac {1} {2}} {\ sqrt {\ frac {\ left (\ mu - \ lambda \ right) \ left (\ nu - \ lambda \ right)} { \ left (A- \ lambda \ right) \ left (B- \ lambda \ right)}}}}

$${\ displaystyle h _ {\ mu} = {\ frac {1} {2}} {\ sqrt {\ frac {\ left (\ nu - \ mu \ right) \ left (\ lambda - \ mu \ right)} { \ left (A- \ mu \ right) \ left (B- \ mu \ right)}}}}

$${\ displaystyle h _ {\ nu} = {\ frac {1} {2}} {\ sqrt {\ frac {\ left (\ lambda - \ nu \ right) \ left (\ mu - \ nu \ right)} { \ left (A- \ nu \ right) \ left (B- \ nu \ right)}}}}

Por lo tanto, el elemento de volumen infinitesimal es igual a

$${\ displaystyle dV = {\ frac {\ left (\ mu - \ lambda \ right) \ left (\ nu - \ lambda \ right) \ left (\ nu - \ mu \ right)} {8 {\ sqrt {\ izquierda (A- \ lambda \ derecha) \ izquierda (B- \ lambda \ derecha) \ izquierda (A- \ mu \ derecha) \ izquierda (\ mu -B \ derecha) \ izquierda (\ nu -A \ derecha) \ izquierda (\ nu -B \ derecha)}}}} \ d \ lambda d \ mu d \ nu}

Operadores diferenciales tales como $${\ displaystyle \ nabla \ cdot \ mathbf {F}} y $${\ displaystyle \ nabla \ times \ mathbf {F}} Se puede expresar en las coordenadas. $${\ displaystyle (\ lambda, \ mu, \ nu)}sustituyendo los factores de escala en las fórmulas generales que se encuentran en las coordenadas ortogonales.

parametrización (o parametrización ; también parametrización , parametrización ) es el proceso de encontrar ecuaciones paramétricas de una curva , una superficie o, más generalmente, una variedad o una variedad , definida por una ecuación implícita . El proceso inverso se llama implicitización . ^[1] "Parametrizar" por sí mismo significa "expresar en términos de parámetros ". ^[2]

La parametrización es un proceso matemático que consiste en expresar el estado de un sistema , proceso o modelo en función de algunas cantidades independientes llamadas parámetros . El estado del sistema generalmente está determinado por un conjunto finito de coordenadas , y la parametrización consiste, por lo tanto, en una función de varias variables reales para cada coordenada. El número de parámetros es el número de grados de libertad del sistema.

Por ejemplo, la posición de un punto que se mueve en una curva en un espacio tridimensional está determinada por el tiempo necesario para alcanzar el punto al comenzar desde un origen fijo. Si x , y , z son las coordenadas del punto, el movimiento se describe así mediante una ecuación paramétrica ^[1]

{\ displaystyle {\ begin {alineado} x & = f (t) \\ y & = g (t) \\ z & = h (t), \ end {alineado}}}

donde t denota el tiempo. Dicha ecuación paramétrica determina completamente la curva, sin la necesidad de ninguna interpretación de t como tiempo, y por eso se llama ecuación paramétrica de la curva (esto a veces se abrevia diciendo que uno tiene una curva paramétrica ). De manera similar, uno obtiene la ecuación paramétrica de una superficie considerando las funciones de dos parámetros t y u .

No-singularidad [ editar ]

Las parametrizaciones no son generalmente únicas . El objeto tridimensional ordinario puede ser parametrizado (o 'coordinado') de manera igualmente eficiente con coordenadas cartesianas (x, y, z), coordenadas polares cilíndricas ( ρ , φ , z ), coordenadas esféricas ( r , φ, θ) u otras sistemas de coordenadas .

De manera similar, el espacio de color de la visión de color tricromática humana se puede parametrizar en términos de los tres colores rojo, verde y azul, RGB , o con cian, magenta, amarillo y negro, CMYK .

Dimensionalidad [ editar ]

En general, el número mínimo de parámetros necesarios para describir un modelo u objeto geométrico es igual a su dimensión , y el alcance de los parámetros, dentro de sus rangos permitidos, es el espacio de parámetros . Aunque un buen conjunto de parámetros permite la identificación de cada punto en el espacio del objeto, puede ser que, para una parametrización dada, diferentes valores de parámetros puedan referirse al mismo punto. Tales mapeos son suryectivos pero no inyectivos . Un ejemplo es el par de coordenadas polares cilíndricas (ρ, φ, z) y (ρ, φ + 2π, z).

Invarianza [ editar ]

Como se indicó anteriormente, existe una arbitrariedad en la elección de los parámetros de un modelo dado, objeto geométrico, etc. A menudo, uno desea determinar las propiedades intrínsecas de un objeto que no dependen de esta arbitrariedad, que por lo tanto son independientes de cualquier elección particular de parámetros Este es particularmente el caso en la física, donde la invariancia de parametrización (o 'invarianza de reparametrización') es un principio guía en la búsqueda de teorías físicamente aceptables (particularmente en la relatividad general ).

Por ejemplo, mientras que la ubicación de un punto fijo en alguna línea curva puede estar dada por un conjunto de números cuyos valores dependen de cómo se parametriza la curva, la longitud (definida adecuadamente) de la curva entre dos de estos puntos fijos será independiente de la elección particular de parametrización (en este caso: el método por el cual un punto arbitrario en la línea se indexa de forma única). La longitud de la curva es, por lo tanto, una cantidad invariante de parametrización. En tales casos, la parametrización es una herramienta matemática empleada para extraer un resultado cuyo valor no depende de, o hace referencia a, los detalles de la parametrización. Más generalmente, la invariancia de la parametrización de una teoría física implica que, o bien la dimensionalidad o el volumen del espacio de parámetros es mayor que el necesario para describir la física (las cantidades de importancia física) en cuestión.

Aunque la teoría de la relatividad general puede expresarse sin hacer referencia a un sistema de coordenadas, los cálculos de cantidades físicas (es decir, observables), como la curvatura del espacio-tiempo, implican invariablemente la introducción de un sistema de coordenadas particular para referirse a los puntos del espacio-tiempo involucrados en el cálculo. . En el contexto de la relatividad general, entonces, la elección del sistema de coordenadas puede considerarse como un método de "parametrización" del espacio-tiempo, y la insensibilidad del resultado de un cálculo de una cantidad físicamente significativa a esa elección puede considerarse como un ejemplo. de la invariancia de parametrización.

Como otro ejemplo, las teorías físicas cuyas cantidades observables dependen solo de las distancias relativas (la relación de distancias) entre pares de objetos se dice que son invariantes en escala . En tales teorías, cualquier referencia en el curso de un cálculo a una distancia absoluta implicaría la introducción de un parámetro para el cual la teoría es invariante.

Ejemplos [ editar ]

Esta lista está incompleta ; Puedes ayudar expandiéndolo .

• Superficie de niño
• La parametrización de McCullagh de las distribuciones de Cauchy.
• Parametrización (clima) , la representación paramétrica de los modelos de circulación general y la predicción numérica del tiempo.
• Perfil de esfera isotérmica singular.
• Modelo Lambda-CDM , el modelo estándar de la cosmología del Big Bang.

Técnicas [ editar ]

Esta lista está incompleta ; Puedes ayudar expandiéndolo .

• Parametrización de feynman
• Parametrización de Schwinger
• Modelado de sólidos
• Inyección de dependencia

la ecuación del pedal de la curva es una relación entre r y pdonde r es la distancia desde O a un punto en C y p es la distancia perpendicular desde O a la línea tangente a Cen el punto. El punto O se llama el punto del pedal y los valores r y p a veces se llaman las coordenadas del pedalde un punto relativo a la curva y al punto del pedal. También es útil medir la distancia de O a la normal.$${\ displaystyle p_ {c}}(la coordenada contrapedal ) aunque no es una cantidad independiente y se relaciona con$${\ displaystyle (r, p)} como $${\ displaystyle p_ {c}: = {\ sqrt {r ^ {2} -p ^ {2}}}}.

Algunas curvas tienen ecuaciones de pedal particularmente simples y conocer la ecuación de pedal de una curva puede simplificar el cálculo de algunas de sus propiedades, como la curvatura. Estas coordenadas también son adecuadas para resolver ciertos tipos de problemas de fuerza en la mecánica clásica y en la mecánica celeste .

Ecuaciones [ editar ]

Coordenadas cartesianas [ editar ]

Para C dada en coordenadas rectangulares por f ( x ,  y ) = 0, y con O como origen, las coordenadas del pedal del punto ( x ,  y ) están dadas por: ^[1]

$${\ displaystyle r = {\ sqrt {x ^ {2} + y ^ {2}}}}

$${\ displaystyle p = {\ frac {x {\ frac {\ parcial f} {\ parcial x}} + y {\ frac {\ parcial f} {\ parcial y}}} {\ sqrt {\ left ({\ frac {\ parcial f} {\ parcial x}} \ derecha) ^ {2} + \ izquierda ({\ frac {\ parcial f} {\ parcial y}} \ derecha) ^ {2}}}}.}

La ecuación del pedal se puede encontrar eliminando x e y de estas ecuaciones y la ecuación de la curva.

La expresión para p se puede simplificar si la ecuación de la curva se escribe en coordenadas homogéneasintroduciendo una variable z , de modo que la ecuación de la curva sea g ( x ,  y ,  z ) = 0. Luego se da el valor de p por ^[2]

$${\ displaystyle p = {\ frac {\ frac {\ partial g} {\ partial z}} {\ sqrt {\ left ({\ frac {\ partial g} {\ partial x}} \ right) ^ {2} + \ left ({\ frac {\ partial g} {\ partial y}} \ right) ^ {2}}}}}

donde el resultado es evaluado en z = 1

Coordenadas polares [ editar ]

Para C dada en coordenadas polares por r  =  f (θ), entonces

$${\ displaystyle p = r \ sin \ phi}

dónde $${\ displaystyle \ phi}es el ángulo tangencial polar dado por

$${\ displaystyle r = {\ frac {dr} {d \ theta}} \ tan \ phi.}

La ecuación del pedal se puede encontrar al eliminar θ de estas ecuaciones. ^[3]

Alternativamente, de lo anterior podemos encontrar que

$${\ displaystyle \ left | {\ frac {dr} {d \ theta}} \ right | = {\ frac {rp_ {c}} {p}},}

dónde $${\ displaystyle p_ {c}: = {\ sqrt {r ^ {2} -p ^ {2}}}}Es la coordenada "contrapedal", es decir, la distancia a la normal. Esto implica que si una curva satisface una ecuación diferencial autónoma en coordenadas polares de la forma:

$${\ displaystyle f \ left (r, \ left | {\ frac {dr} {d \ theta}} \ right | \ right) = 0,}

su ecuación de pedal se convierte en

$${\ displaystyle f \ left (r, {\ frac {rp_ {c}} {p}} \ right) = 0.}

Ejemplo [ editar ]

Como ejemplo, tome la espiral logarítmica con el ángulo en espiral α:

$${\ displaystyle r = ae ^ {{\ frac {\ cos \ alpha} {\ sin \ alpha}} \ theta}.}

Diferenciación con respecto a $${\ displaystyle \ theta} obtenemos

$${\ displaystyle {\ frac {dr} {d \ theta}} = {\ frac {\ cos \ alpha} {\ sin \ alpha}} ae ^ {{\ frac {\ cos \ alpha} {\ sin \ alpha} } \ theta} = {\ frac {\ cos \ alpha} {\ sin \ alpha}} r,}

por lo tanto

$${\ displaystyle \ left | {\ frac {dr} {d \ theta}} \ right | = \ left | {\ frac {\ cos \ alpha} {\ sin \ alpha}} \ right | r,}

Y así, en las coordenadas del pedal obtenemos

$${\ displaystyle {\ frac {r} {p}} p_ {c} = \ left | {\ frac {\ cos \ alpha} {\ sin \ alpha}} \ right | r, \ qquad \ Rightarrow \ qquad | \ sin \ alpha | p_ {c} = | \ cos \ alpha | p,}

o usando el hecho de que $${\ displaystyle p_ {c} ^ {2} = r ^ {2} -p ^ {2}} obtenemos

$${\ displaystyle p = | \ sin \ alpha | r.}

Este enfoque puede generalizarse para incluir ecuaciones diferenciales autónomas de cualquier orden de la siguiente manera: ^[4] Una curva C que es una solución de una ecuación diferencial autónoma de orden n .$${\ displaystyle n \ geq 1}) en coordenadas polares

$${\ displaystyle f \ left (r, | r '_ {\ theta} |, r' '_ {\ theta}, | r' '' _ {\ theta} | \ dots, r _ {\ theta} ^ {( 2j)}, | r _ {\ theta} ^ {(2j + 1)} |, \ dots, r _ {\ theta} ^ {(n)} \ right) = 0,}

es la curva del pedal de una curva dada en coordenadas del pedal por

$${\ displaystyle f (p, p_ {c}, p_ {c} p_ {c} ', p_ {c} (p_ {c} p_ {c}') ', \ dots, (p_ {c} \ parcial _ {p}) ^ {n} p) = 0,}

Donde la diferenciación se hace con respecto a $${\ displaystyle p}.

Problemas de fuerza [ editar ]

Las soluciones a algunos problemas de fuerza de la mecánica clásica pueden ser sorprendentemente fáciles de obtener en las coordenadas del pedal.

Considere un sistema dinámico:

$${\ displaystyle {\ ddot {x}} = F ^ {\ prime} (| x | ^ {2}) x + 2G ^ {\ prime} (| x | ^ {2}) {\ dot {x}} ^ {\ perp},}

Describiendo una evolución de una partícula de prueba (con posición $${\ displaystyle x} y velocidad $${\ displaystyle {\ dot {x}}}) en el plano en presencia de centrales $${\ displaystyle F} y Lorentz gusta $${\ displaystyle G}potencial. Las cantidades:

$${\ displaystyle L = x \ cdot {\ dot {x}} ^ {\ perp} + G (| x | ^ {2}), \ qquad c = | {\ dot {x}} | ^ {2} - F (| x | ^ {2}),}

Se conservan en este sistema.

Luego la curva trazada por $${\ displaystyle x} se da en coordenadas del pedal por

$${\ displaystyle {\ frac {\ left (LG (r ^ {2}) \ right) ^ {2}} {p ^ {2}}} = F (r ^ {2}) + c,}

con el punto de pedal en el origen. Este hecho fue descubierto por P. Blaschke en 2017. ^[5]

Ejemplo [ editar ]

Como ejemplo, considere el llamado problema de Kepler , es decir, el problema de la fuerza central, donde la fuerza varía inversamente como un cuadrado de la distancia:

$${\ displaystyle {\ ddot {x}} = - {\ frac {M} {| x | ^ {3}}} x,}

Podemos llegar a la solución inmediatamente en coordenadas de pedal.

$${\ displaystyle {\ frac {L ^ {2}} {p ^ {2}}} = {\ frac {2M} {r}} + c,},

dónde $${\ displaystyle L} corresponde al momento angular de la partícula y $${\ displaystyle c}a su energía. Así hemos obtenido la ecuación de una sección cónica en coordenadas de pedal.

A la inversa, para una curva C dada , podemos deducir fácilmente qué fuerzas tenemos que imponer sobre una partícula de prueba para moverse a lo largo de ella.

Ecuaciones de pedal para curvas específicas [ editar ]

Espirales sinusoidales [ editar ]

Para una espiral sinusoidal escrita en la forma.

$${\ displaystyle r ^ {n} = a ^ {n} \ sin (n \ theta)}

el angulo tangencial polar es

$${\ displaystyle \ psi = n \ theta}

que produce la ecuación del pedal

$${\ displaystyle pa ^ {n} = r ^ {n + 1}.}

La ecuación del pedal para una serie de curvas familiares se puede obtener ajustando n a valores específicos: ^[6]

norte	Curva	Punto de pedal	Pedal eq.
1	Circulo con radio a	Punto en la circunferencia	pa = r 2
−1	Línea	Distancia de puntos a de la línea	p = a
1 / 2	Cardioide	Cúspide	p 2 a = r 3
- 1 / 2	Parábola	Atención	p 2 = ar
2	Lemniscado de Bernoulli	Centrar	pa 2 = r 3
−2	Hipérbola rectangular	Centrar	rp = a 2

Espirales [ editar ]

Una curva en forma de espiral de la forma.

$${\ displaystyle r = c \ theta ^ {\ alpha},}

satisface la ecuación

$${\ displaystyle {\ frac {dr} {d \ theta}} = \ alpha r ^ {\ frac {\ alpha -1} {\ alpha}},

y por lo tanto se puede convertir fácilmente en coordenadas de pedal como

$${\ displaystyle {\ frac {1} {p ^ {2}}} = {\ frac {\ alpha ^ {2} c ^ {\ frac {2} {\ alpha}}} {r ^ {2 + {\ frac {2} {\ alpha}}}}} + {\ frac {1} {r ^ {2}}}.}

Los casos especiales incluyen:

$${\ displaystyle \ alpha}	Curva	Punto de pedal	Pedal eq.
1	Espiral de Arquímedes	Origen	$${\ displaystyle {\ frac {1} {p ^ {2}}} = {\ frac {1} {r ^ {2}}} + {\ frac {c ^ {2}} {r ^ {4}} }}
−1	Espiral hiperbólica	Origen	$${\ displaystyle {\ frac {1} {p ^ {2}}} = {\ frac {1} {r ^ {2}}} + {\ frac {1} {c ^ {2}}}}
1 / 2	Espiral de fermat	Origen	$${\ displaystyle {\ frac {1} {p ^ {2}}} = {\ frac {1} {r ^ {2}}} + {\ frac {c ^ {4}} {4r ^ {6}} }}
- 1 / 2	Lituus	Origen	$${\ displaystyle {\ frac {1} {p ^ {2}}} = {\ frac {1} {r ^ {2}}} + {\ frac {r ^ {2}} {4c ^ {4}} }}

Epi y hipocicloides [ editar ]

Para un epi o hipocicloide dado por ecuaciones paramétricas

$${\ displaystyle x (\ theta) = (a + b) \ cos \ theta -b \ cos \ left ({\ frac {a + b} {b}} \ theta \ right)}

$${\ displaystyle y (\ theta) = (a + b) \ sin \ theta -b \ sin \ left ({\ frac {a + b} {b}} \ theta \ right),}

La ecuación del pedal con respecto al origen es ^[7].

$${\ displaystyle r ^ {2} = a ^ {2} + {\ frac {4 (a + b) b} {(a + 2b) ^ {2}}} p ^ {2}}

o ^[8]

$${\ displaystyle p ^ {2} = A (r ^ {2} -a ^ {2})}

con

$${\ displaystyle A = {\ frac {(a + 2b) ^ {2}} {4 (a + b) b}}.}

Los casos especiales obtenidos mediante el establecimiento de b = ^un / _n para valores específicos de n incluyen:

norte	Curva	Pedal eq.
1, - 1 / 2	Cardioide	$${\ displaystyle p ^ {2} = {\ frac {9} {8}} (r ^ {2} -a ^ {2})}
2, - 2 / 3	Nefroide	$${\ displaystyle p ^ {2} = {\ frac {4} {3}} (r ^ {2} -a ^ {2})}
-3, - 3 / 2	Deltoides	$${\ displaystyle p ^ {2} = - {\ frac {1} {8}} (r ^ {2} -a ^ {2})}
-4, - 4 / 3	Astroide	$${\ displaystyle p ^ {2} = - {\ frac {1} {3}} (r ^ {2} -a ^ {2})}

Otras curvas [ editar ]

Otras ecuaciones del pedal son:, ^[9]

Curva	Ecuación	Punto de pedal	Pedal eq.
Línea	$${\ displaystyle ax + by + c = 0}	Origen	$${\ displaystyle p = {\ frac {| c |} {\ sqrt {a ^ {2} + b ^ {2}}}}}
Punto	$${\ displaystyle (x_ {0}, y_ {0})}	Origen	$${\ displaystyle r = {\ sqrt {x_ {0} ^ {2} + y_ {0} ^ {2}}}}
Circulo	$${\ displaystyle | xa | = R}	Origen	$${\ displaystyle 2pR = r ^ {2} + R ^ {2} - | a | ^ {2}}
Involucrar de un círculo	$${\ displaystyle r = {\ frac {a} {\ cos \ alpha}}, \ \ theta = \ tan \ alpha - \ alpha}	Origen	$${\ displaystyle p_ {c} = | a |}
Elipse	$${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 1}	Centrar	$${\ displaystyle {\ frac {a ^ {2} b ^ {2}} {p ^ {2}}} + r ^ {2} = a ^ {2} + b ^ {2}}
Hipérbola	$${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}} = 1}	Centrar	$${\ displaystyle - {\ frac {a ^ {2} b ^ {2}} {p ^ {2}}} + r ^ {2} = a ^ {2} -b ^ {2}}
Elipse	$${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 1}	Atención	$${\ displaystyle {\ frac {b ^ {2}} {p ^ {2}}} = {\ frac {2a} {r}} - 1}
Hipérbola	$${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}} = 1}	Atención	$${\ displaystyle {\ frac {b ^ {2}} {p ^ {2}}} = {\ frac {2a} {r}} + 1}
Espiral logaritmica	$${\ displaystyle r = ae ^ {\ theta \ cot \ alpha}}	Polo	$${\ displaystyle p = r \ sin \ alpha}
Ovalo cartesiano	$${\ displaystyle | x | + \ alpha | xa | = C,}	Atención	$${\ displaystyle {\ frac {(b- (1- \ alpha ^ {2}) r ^ {2}) ^ {2}} {4p ^ {2}}} = {\ frac {Cb} {r}} + (1- \ alpha ^ {2}) Cr - ((1- \ alpha ^ {2}) C ^ {2} + b), \ b: = C ^ {2} - \ alpha ^ {2} | a | ^ {2}}
Óvalo de cassini	$${\ displaystyle | x || xa | = C,}	Atención	$${\ displaystyle {\ frac {(3C ^ {2} + r ^ {4} - | a | ^ {2} r ^ {2}) ^ {2}} {p ^ {2}}} = 4C ^ { 2} \ left ({\ frac {2C ^ {2}} {r ^ {2}}} + 2r ^ {2} - | a | ^ {2} \ right).}
Óvalo de cassini	$${\ displaystyle | xa || x + a | = C,}	Centrar	$${\ displaystyle 2Rpr = r ^ {4} + R ^ {2} - | a | ^ {2}.}