| Parte de una serie en |
| Tiempo espacial |
|---|
 |
| Relatividad especial Relatividad general. |
En física , las transformaciones de Lorentz son una familia de transformaciones lineales de un parámetro de un marco de coordenadas en el espacio-tiempo a otro marco que se mueve a una velocidad constante, el parámetro, dentro del primero. Las transformaciones llevan el nombre del físico holandés Hendrik Lorentz . La transformación inversa respectiva es entonces parametrizada por el negativo de esta velocidad.
La forma más común de transformación, parametrizada por la constante real. que representa una velocidad limitada a la dirección x , se expresa como [1]
donde ( t , x , y , z ) y ( t ′, x ′, y ′, z ′) son las coordenadas de un evento en dos cuadros, donde el cuadro imprimado se ve desde el cuadro no imprimido mientras se mueve con la velocidad v a lolargo el eje x , c es la velocidad de la luz , yEs el factor de Lorentz .
Los marcos de referencia se pueden dividir en dos grupos: inercial (movimiento relativo con velocidad constante) y no inercial (aceleración, movimiento en trayectorias curvas, movimiento de rotación con velocidad angular constante , etc.). El término "transformaciones de Lorentz" solo se refiere a las transformaciones entre marcos inerciales , generalmente en el contexto de la relatividad especial.
En cada marco de referencia , un observador puede usar un sistema de coordenadas local (más exclusivamente coordenadas cartesianas en este contexto) para medir longitudes, y un reloj para medir intervalos de tiempo. Un observador es una entidad real o imaginaria que puede tomar medidas, digamos los humanos, o cualquier otro organismo vivo, o incluso robots y computadoras. Un evento es algo que sucede en un punto en el espacio en un instante de tiempo, o más formalmente un punto en el espacio-tiempo . Las transformaciones conectan las coordenadas de espacio y tiempo de un evento según lo mide un observador en cada fotograma. [nb 1]
Superan la transformación galileana de la física newtoniana , que supone un espacio y un tiempo absolutos (véase la relatividad galileana ). La transformación de Galileo es una buena aproximación solo a velocidades relativas mucho más pequeñas que la velocidad de la luz. Las transformaciones de Lorentz tienen una serie de características no intuitivas que no aparecen en las transformaciones de Galileo. Por ejemplo, reflejan el hecho de que los observadores que se mueven a diferentes velocidades pueden medir diferentes distancias , tiempos transcurridos e incluso diferentes ordenamientos de eventos , pero siempre de manera tal que la velocidad de la luzEs el mismo en todos los marcos de referencia inerciales. La invariancia de la velocidad de la luz es uno de los postulados de la relatividad especial .
Históricamente, las transformaciones fueron el resultado de los intentos de Lorentz y otros para explicar cómo se observó que la velocidad de la luz era independiente del marco de referencia , y para comprender las simetrías de las leyes del electromagnetismo . La transformación de Lorentz está de acuerdo con la relatividad especial , pero se derivó antes de la relatividad especial.
La transformación de Lorentz es una transformación lineal . Puede incluir una rotación del espacio; una transformación de Lorentz sin rotación se llama impulso de Lorentz . En el espacio de Minkowski , el modelo matemático del espacio-tiempo en la relatividad especial, las transformaciones de Lorentz preservan el intervalodel espacio-tiempo entre dos eventos. Esta propiedad es la propiedad definitoria de una transformación de Lorentz. Describen solo las transformaciones en las que el evento de espacio-tiempo en el origen se deja fijo. Pueden considerarse como una rotación hiperbólica del espacio de Minkowski. El conjunto más general de transformaciones que también incluye traducciones se conoce como el grupo de Poincaré .
Historia [ editar ]
Muchos físicos, incluyendo Woldemar Voigt , George FitzGerald , Joseph Larmor y Hendrik Lorentz [3] sí mismo, había estado discutiendo la física implicada por estas ecuaciones desde 1887. [4] A principios de 1889, Oliver Heaviside había mostrado desde las ecuaciones de Maxwell que la eléctrica El campo que rodea una distribución esférica de carga debe dejar de tener simetría esférica.una vez que la carga está en movimiento en relación con el éter. FitzGerald entonces conjeturó que el resultado de distorsión de Heaviside podría aplicarse a una teoría de fuerzas intermoleculares. Algunos meses más tarde, FitzGerald publicó la conjetura de que los cuerpos en movimiento se están contrayendo, para explicar el resultado desconcertante del experimento de Michelson y Morley sobre el viento de éter de 1887 . En 1892, Lorentz presentó de forma independiente la misma idea de una manera más detallada, que posteriormente se denominó hipótesis de contracción de FitzGerald-Lorentz . [5] Su explicación fue ampliamente conocida antes de 1905. [6]
Lorentz (1892–1904) y Larmor (1897–1900), quienes creían la hipótesis del éter luminífero , también buscaron la transformación bajo la cual las ecuaciones de Maxwell son invariantes cuando se transforman del éter al marco en movimiento. Se amplió la contracción de FitzGerald-Lorentz hipótesis y se encontró que la coordenada de tiempo tiene que ser modificado, así ( " hora local "). Henri Poincaré dio una interpretación física a la hora local (a primer orden en v / c , la velocidad relativa de los dos cuadros de referencia normalizados a la velocidad de la luz) como consecuencia de la sincronización del reloj, bajo el supuesto de que la velocidad de la luz es constante En marcos en movimiento.[7] Se reconoce que Larmor fue el primero en comprender lapropiedadcrucial de ladilatación del tiempo inherente a sus ecuaciones. [8]
En 1905, Poincaré fue el primero en reconocer que la transformación tiene las propiedades de un grupo matemático , y la llamó así por Lorentz. [9] Más tarde, en el mismo año, Albert Einstein publicó lo que ahora se llama relatividad especial , derivando la transformación de Lorentz bajo los supuestos del principio de relatividady la constancia de la velocidad de la luz en cualquier marco de referencia inercial , y abandonando el mecanicismo. Aether como innecesario. [10]
Derivación del grupo de transformaciones de Lorentz [ editar ]
Un evento es algo que sucede en un cierto punto en el espacio-tiempo, o más generalmente, el punto en el mismo espacio-tiempo. En cualquier marco inercial, un evento se especifica mediante una coordenada de tiempo ct y un conjunto de coordenadas cartesianas x , y , z para especificar la posición en el espacio en ese marco. Los subíndices etiquetan eventos individuales.
- ( D1 )
En todos los cuadros inerciales para eventos conectados por señales luminosas . La cantidad a la izquierda se denomina intervalo espacio-tiempo entre los eventos a 1 = ( t 1 , x 1 , y 1 , z 1 ) y a 2 = ( t 2 , x 2 , y 2 , z 2 ) . El intervalo entre cualesquiera doslos eventos, no necesariamente separados por señales luminosas, son de hecho invariantes, es decir, independientes del estado de movimiento relativo de los observadores en diferentes marcos de inercia, como se muestra usando homogeneidad e isotropía del espacio . La transformación buscada debe por lo tanto poseer la propiedad que
- ( D2 )
![{\ displaystyle {\ begin {alineado} & c ^ {2} (t_ {2} -t_ {1}) ^ {2} - (x_ {2} -x_ {1}) ^ {2} - (y_ {2 } -y_ {1}) ^ {2} - (z_ {2} -z_ {1}) ^ {2} \\ [6pt] = {} & c ^ {2} (t_ {2} '- t_ {1 } ') ^ {2} - (x_ {2}' - x_ {1} ') ^ {2} - (y_ {2}' - y_ {1} ') ^ {2} - (z_ {2}' -z_ {1} ') ^ {2} \ quad {\ text {(todos los eventos 1, 2)}}. \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d685ef5891f02b82c2656cc341f2016d231c4549)
donde ( ct , x , y , z ) son las coordenadas del espacio-tiempo utilizadas para definir eventos en un cuadro, y ( ct ′, x ′, y ′, z ′) son las coordenadas en otro cuadro. En primer lugar se observa que (D2) se satisface si una arbitraria 4 tupla b de números se añaden a los eventos un 1 y un 2 . Tales transformaciones se denominan traducciones de espacio-tiempo y no se tratan más aquí. Entonces se observa que un lineal Solución preservando el origen del problema más simple.
- ( D3 )
![{\ displaystyle {\ begin {alineado} & c ^ {2} t ^ {2} -x ^ {2} -y ^ {2} -z ^ {2} = c ^ {2} t '^ {2} - x '^ {2} -y' ^ {2} -z '^ {2} \\ [6pt] {\ text {o}} \ quad & c ^ {2} t_ {1} t_ {2} -x_ { 1} x_ {2} -y_ {1} y_ {2} -z_ {1} z_ {2} = c ^ {2} t '_ {1} t' _ {2} -x '_ {1} x '_ {2} -y' _ {1} y '_ {2} -z' _ {1} z '_ {2} \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f78e5280c899e10f32769743cf58e272651c33e4)
resuelve el problema general también. (Una solución que satisfaga la fórmula de la izquierda satisface automáticamente la fórmula correcta, ver identidad de polarización ). Encontrar la solución para el problema más simple es solo una cuestión de búsqueda en la teoría de grupos clásicos que conservan formas bilineales de varias firmas. [nb 2] La primera ecuación en (D3) se puede escribir de forma más compacta como
- ( D4 )
donde (,) se refiere a la forma bilineal de firma (1, 3) en ℝ 4 expuesta a la derecha fórmula lado en (D3) . La notación alternativa definida a la derecha se conoce como el producto de punto relativista . Spacetime matemáticamente vista como ℝ 4 dotado de esta forma bilineal se conoce como Minkowski espacio M . La transformación de Lorentz es, por lo tanto, un elemento del grupo de Lorentz O (1, 3) , el grupo de Lorentz o, para aquellos que prefieren la otra firma métrica , O (3, 1) (también llamado el grupo de Lorentz).[nb 3] Uno tiene
- ( D5 )
que es precisamente la preservación de la forma bilineal (D3) que implica (por linealidad de Λ y bilinealidad de la forma) que (D2) es satisfecho. Los elementos del grupo de Lorentz son rotaciones y refuerzos y mezclas de los mismos. Si se incluyen las traducciones del espacio-tiempo, entonces se obtiene el grupo de Lorentz no homogéneo o el grupo de Poincaré .
Generalidades [ editar ]
Las relaciones entre las coordenadas del espacio-tiempo imprimadas y no imprimadas son las transformaciones de Lorentz , cada coordenada en un cuadro es una función lineal de todas las coordenadas en el otro cuadro, y las funciones inversas son la transformación inversa. Dependiendo de cómo se mueven los fotogramas entre sí y de cómo están orientados en el espacio entre sí, otros parámetros que describen la dirección, la velocidad y la orientación entran en las ecuaciones de transformación.
Las transformaciones que describen el movimiento relativo con velocidad constante (uniforme) y sin rotación de los ejes de coordenadas del espacio se denominan impulsos , y la velocidad relativa entre los cuadros es el parámetro de la transformación. El otro tipo básico de transformaciones de Lorentz son las rotaciones en las coordenadas espaciales solamente, estos también son marcos inerciales, ya que no hay movimiento relativo, los cuadros están simplemente inclinados (y no giran continuamente), y en este caso las cantidades que definen la rotación son los parámetros de la transformación (p. ej., representación del ángulo del eje , o ángulos de Euler , etc.). Una combinación de una rotación y un impulso es una transformación homogénea , que transforma el origen de nuevo en el origen.
El grupo completo de Lorentz O (3, 1) también contiene transformaciones especiales que no son rotaciones ni impulsos, sino reflexiones en un plano a través del origen. Dos de estos pueden ser seleccionados; inversión espacial en la que las coordenadas espaciales de todos los eventos se invierten en signo e inversión temporal en la que la coordenada de tiempo para cada evento obtiene su signo invertido.
Los refuerzos no deben combinarse con meros desplazamientos en el espacio-tiempo; en este caso, los sistemas de coordenadas simplemente se desplazan y no hay movimiento relativo. Sin embargo, estas también cuentan como simetrías forzadas por la relatividad especial, ya que dejan el intervalo espacio-tiempo invariante. Una combinación de una rotación con un impulso, seguida de un cambio en el espacio-tiempo, es una transformación de Lorentz no homogénea , un elemento del grupo de Poincaré, que también se denomina grupo de Lorentz no homogéneo.
Fórmula física de Lorentz refuerza [ editar ]
Transformación de coordenadas [ editar ]
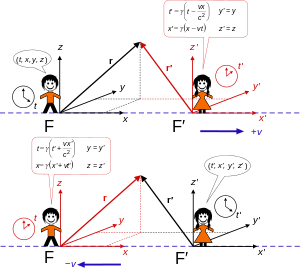
Un observador "estacionario" en el cuadro F define eventos con coordenadas t , x , y , z . Otro cuadro F ′ se mueve con la velocidad v relativa a F , y un observador en este cuadro "en movimiento" F ′ define los eventos utilizando las coordenadas t ′, x ′, y ′, z ′ .
Los ejes de coordenadas en cada cuadro son paralelos (los ejes x y x ' son paralelos, los ejes y e y ' son paralelos, y los ejes z y z ' son paralelos), permanecen mutuamente perpendiculares, y el movimiento relativo es a lo largo de la coincidencia xx ′ Ejes. En t = t ′ = 0 , los orígenes de ambos sistemas de coordenadas son los mismos, ( x, y, z ) = ( x ′, y ′, z ′) = (0, 0, 0). En otras palabras, los tiempos y las posiciones son coincidentes en este evento. Si todos estos se mantienen, entonces se dice que los sistemas de coordenadas están en configuración estándaro sincronizados .
Si un observador en F registra un evento t, x, y, z , entonces un observador en F ′ registra el mismo evento con coordenadas [12]
Lorentz boost ( x direccion )
Aquí, v es el parámetro de la transformación, para un impulso dado es un número constante, pero puede tomar un rango continuo de valores. En la configuración utilizada aquí, la velocidad relativa positiva v > 0 es un movimiento a lo largo de las direcciones positivas de los ejes xx ′ , la velocidad relativa cero v = 0 no es un movimiento relativo, mientras que la velocidad relativa negativa v <0 font=""> es un movimiento relativo a lo largo de las direcciones negativas de el xx ' ejes. La magnitud de la velocidad relativa v no puede ser igual o superior a c , por lo que solo las velocidades subluminales - c <v < c están permitidos. El rango correspondiente de γ es1 ≤ γ <∞ .
Las transformaciones no se definen si v está fuera de estos límites. A la velocidad de la luz ( v = c ) γ es infinito, y más rápido que la luz ( v > c ) γ es un número complejo , cada uno de los cuales hace que las transformaciones no sean físicas. Las coordenadas de espacio y tiempo son cantidades medibles y numéricamente deben ser números reales.
Como una transformación activa , un observador en F ′ advierte que las coordenadas del evento deben ser "aumentadas" en las direcciones negativas de los ejes xx ′ , debido a - v en las transformaciones. Esto tiene el efecto equivalente del sistema de coordenadas F 'reforzado en las direcciones positivas de los ejes xx ' , mientras que el evento no cambia y simplemente se representa en otro sistema de coordenadas, una transformación pasiva .
Las relaciones inversas ( t , x , y , z en términos de t ′, x ′, y ′, z ′ ) se pueden encontrar al resolver algebraicamente el conjunto original de ecuaciones. Una forma más eficiente es usar principios físicos. Aquí F ′es el marco "estacionario", mientras que F es el marco "en movimiento". De acuerdo con el principio de relatividad, no hay un marco de referencia privilegiado, por lo que las transformaciones de F ′ a F deben tomar exactamente la misma forma que las transformaciones de F a F ′. La única diferencia es que F se mueve con velocidad , v en relación con F ′ (es decir, la velocidad relativa tiene la misma magnitud pero está dirigida de manera opuesta). Así, si un observador en F ′ anota un evento t ′, x ′, y ′, z ′ , entonces un observador en Fanota el mismo evento con coordenadas
Lorentz impulso inverso ( x dirección )
y el valor de γ permanece sin cambios. Este "truco" de simplemente invertir la dirección de la velocidad relativa al mismo tiempo que conserva su magnitud, y al intercambiar variables imprimadas y no imprimadas, siempre se aplica para encontrar la transformación inversa de cada impulso en cualquier dirección.
Lo que demuestra mucho más claramente la simetría en la transformación. De los rangos permitidos de v y la definición de β , sigue a −1 < β <1 font=""> . El uso de β y γ es estándar en toda la literatura.
Las transformaciones de Lorentz también pueden derivarse de una manera que se asemeja a las rotaciones circulares en el espacio 3d utilizando las funciones hiperbólicas . Para el impulso en la dirección x , los resultados son
Lorentz boost ( x dirección con rapidez ζ )
donde ζ ( zeta en minúscula ) es un parámetro llamado rapidez (se usan muchos otros símbolos, incluidos θ, ϕ, φ, η, ψ, ξ ). Dada la gran semejanza con las rotaciones de coordenadas espaciales en el espacio 3d en los planos cartesiano xy, yz y zx, un refuerzo de Lorentz puede considerarse como una rotación hiperbólica de coordenadas del espacio-tiempo en los planos de tiempo cartesiano xt, yt y zt 4d espacio minkowski . El parámetro ζ es el ángulo de rotación hiperbólico , análogo al ángulo ordinario para rotaciones circulares. Esta transformación se puede ilustrar con un diagrama de Minkowski .
Las funciones hiperbólicas surgen de la diferencia entre los cuadrados del tiempo y las coordenadas espaciales en el intervalo espacio-tiempo, en lugar de una suma. La importancia geométrica de las funciones hiperbólicas se puede visualizar tomando x = 0 o ct = 0 en las transformaciones. Al cuadrar y restar los resultados, se pueden derivar curvas hiperbólicas de valores de coordenadas constantes pero variando ζ , que parametriza las curvas según la identidad.
A la inversa, los ejes ct y x pueden construirse para coordenadas variables pero con constante ζ . La definición
proporciona el enlace entre un valor constante de rapidez y la pendiente del eje ct en el espacio-tiempo. Una consecuencia de estas dos fórmulas hiperbólicas es una identidad que coincide con el factor de Lorentz
Comparando las transformaciones de Lorentz en términos de velocidad relativa y velocidad, o usando las fórmulas anteriores, las conexiones entre β , γ y ζ son
Tomando la tangente inversa hiperbólica da la rapidez.
Como −1 < β <1 font=""> , sigue a −∞ < ζ <∞ . De la relación entre ζ y β , la rapidez positiva ζ > 0 es un movimiento a lo largo de las direcciones positivas de los ejes xx ′ , la rapidez cero ζ = 0 no es un movimiento relativo, mientras que la velocidad negativa ζ <0 font=""> es un movimiento relativo a lo largo de las direcciones negativas del xx ′ ejes.
Las transformaciones inversas se obtienen intercambiando cantidades imprimadas y no imprimadas para cambiar los marcos de coordenadas y negando la rapidez ζ → - ζ ya que esto es equivalente a negar la velocidad relativa. Por lo tanto,
Refuerzo de Lorentz inverso ( x dirección con rapidez ζ )
Las transformaciones inversas pueden visualizarse de manera similar considerando los casos en que x ′ = 0 y ct ′ = 0 .
Hasta ahora, las transformaciones de Lorentz se han aplicado a un evento . Si hay dos eventos, hay una separación espacial y un intervalo de tiempo entre ellos. De la linealidad de las transformaciones de Lorentz se deduce que se pueden elegir dos valores de coordenadas de espacio y tiempo, las transformaciones de Lorentz se pueden aplicar a cada una y luego restar para obtener las transformaciones de Lorentz de las diferencias;
con relaciones inversas
donde Δ ( delta en mayúsculas ) indica una diferencia de cantidades; por ejemplo, Δ x = x 2 - x 1 para dos valores de coordenadas x , y así sucesivamente.
Estas transformaciones en diferencias en lugar de puntos espaciales o instantes de tiempo son útiles por varias razones:
- en cálculos y experimentos, son las longitudes entre dos puntos o intervalos de tiempo que se miden o son de interés (por ejemplo, la longitud de un vehículo en movimiento o la duración del tiempo que se tarda en viajar de un lugar a otro),
- las transformaciones de la velocidad se pueden derivar fácilmente haciendo que la diferencia sea infinitamente pequeña y dividiendo las ecuaciones, y el proceso se repita para la transformación de la aceleración,
- si los sistemas de coordenadas nunca son coincidentes (es decir, no en la configuración estándar), y si ambos observadores pueden ponerse de acuerdo sobre un evento t 0 , x 0 , y 0 , z 0 en F y t 0 ', x 0 ', y 0 ' , z 0 ′ en F ′ , entonces pueden usar ese evento como el origen, y las diferencias de coordenadas del espacio-tiempo son las diferencias entre sus coordenadas y este origen, por ejemplo, Δ x = x - x 0 ,Δ x ′ = x ′ - x 0 ′ , etc.
Implicaciones físicas [ editar ]
Un requisito crítico de las transformaciones de Lorentz es la invariancia de la velocidad de la luz, un hecho utilizado en su derivación y contenido en las transformaciones mismas. Si en F la ecuación para un pulso de luz a lo largo de la dirección x es x = ct , entonces en F ′ las transformaciones de Lorentz dan x ′ = ct ′ , y viceversa, para cualquier - c < v < c .
Para velocidades relativas mucho menores que la velocidad de la luz, las transformaciones de Lorentz se reducen a la transformación de Galilea.
De acuerdo con el principio de correspondencia . A veces se dice que la física no relativista es una física de "acción instantánea a distancia". [13]
Tres predicciones contraintuitivas, pero correctas, de las transformaciones son:
- Relatividad de la simultaneidad.
- Supongamos que dos eventos ocurren simultáneamente ( Δ t = 0 ) a lo largo del eje x, pero separados por un desplazamiento distinto de cero Δ x . Entonces en F ′ , encontramos que, por lo que los eventos ya no son simultáneos de acuerdo con un observador en movimiento.
- Dilatación del tiempo
- Supongamos que hay un reloj en reposo en F . Si un intervalo de tiempo se mide en el mismo punto en ese cuadro, de modo que Δ x = 0 , entonces las transformaciones dan este intervalo en F ′ por Δ t ′ = γ Δ t . A la inversa, supongamos que hay un reloj en reposo en F ′ . Si un intervalo se mide en el mismo punto en ese cuadro, de modo que Δ x ′ = 0 , entonces las transformaciones dan este intervalo en F por Δ t = γ Δ t ′. De cualquier manera, cada observador mide el intervalo de tiempo entre tics de un reloj en movimiento para que sea más largo en un factor γ que el intervalo de tiempo entre tics de su propio reloj.
- Contracción de longitud
- Supongamos que hay una varilla en reposo en F alineada a lo largo del eje x, con una longitud Δ x . En F ′ , la barra se mueve con velocidad - v , por lo que su longitud debe medirse tomando dos mediciones simultáneas ( Δ t ′ = 0 ) en los extremos opuestos. En estas condiciones, la transformación inversa de Lorentz muestra que Δ x = γ Δ x ′ . En F, las dos mediciones ya no son simultáneas, pero esto no importa porque la varilla está en reposo en F. Así que cada observador mide la distancia entre los puntos finales de una barra móvil para que sea más corta en un factor 1 / γ que los puntos finales de una barra idéntica en reposo en su propio marco. La contracción de la longitud afecta a cualquier cantidad geométrica relacionada con las longitudes, por lo que desde la perspectiva de un observador en movimiento, las áreas y los volúmenes también aparecerán reducidos a lo largo de la dirección del movimiento.
No hay comentarios:
Publicar un comentario