OCEANOGRAFÍA FÍSICA

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Una extensión de madera a la deriva a lo largo de la costanorte del estado de Washington . La deriva de Stokes, además de la deriva de Ekman y las corrientes geostróficas , es uno de los procesos relevantes en el transporte de desechos marinos. ^[1]

Stokes deriva en olas de aguas profundas, con una longitud de onda de aproximadamente el doble de la profundidad del agua. Haga clic aquí para ver una animación (4.15 MB). 
Descripción (también de la animación) : 
Los círculos rojos son las posiciones actuales de las partículas sin masa, que se mueven con la velocidad del flujo . La línea azul claro indica la trayectoria de estas partículas, y el azul claro rodea la posición de las partículas después de cada período de onda . Los puntos blancos son partículas fluidas, también seguidas en el tiempo. En el caso mostrado aquí, la media velocidad horizontal euleriano debajo de la onda a través es cero. 
Observe que el período de onda, experimentada por una partícula fluida cerca de la superficie libre , es diferente del período de onda en una posición horizontal fija (como lo indican los círculos de color azul claro). Esto se debe al cambio Doppler .

Stokes deriva en olas de aguas poco profundas , con una longitud de onda mucho más larga que la profundidad del agua. Haga clic aquí para ver una animación (1.29 MB). 
Descripción (también de la animación) : 
Los círculos rojos son las posiciones actuales de las partículas sin masa, que se mueven con la velocidad del flujo . La línea azul claro indica la trayectoria de estas partículas, y el azul claro rodea la posición de las partículas después de cada período de onda . Los puntos blancos son partículas fluidas, también seguidas en el tiempo. En el caso mostrado aquí, la media velocidad horizontal euleriano debajo de la onda a través es cero. 
Observe que el período de onda, experimentada por una partícula fluida cerca de la superficie libre , es diferente del período de onda en una posición horizontal fija (como lo indican los círculos de color azul claro). Esto se debe al cambio Doppler .

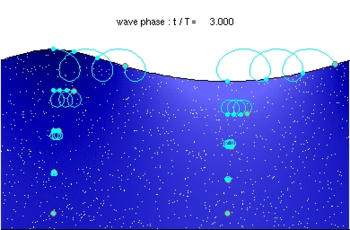
Para un movimiento de onda puro en dinámica de fluidos , la velocidad de deriva de Stokes es la velocidad promedio cuando se sigue una parcela de fluido específica a medida que viaja con el flujo de fluido . Por ejemplo, una partícula que flota en la superficie libre de las ondas de agua , experimenta una velocidad de deriva neta de Stokes en la dirección de la propagación de la onda .

Más generalmente, la velocidad de deriva de Stokes es la diferencia entre la velocidad de flujo de Lagrangian promedio de una parcela de fluido y la velocidad de flujo de Eulerian promedio del fluido en una posición fija. Este fenómeno no lineal lleva el nombre de George Gabriel Stokes , quien derivó expresiones para esta deriva en su estudio de 1847 sobre las ondas del agua .

La deriva de Stokes es la diferencia en las posiciones finales, después de una cantidad de tiempo predefinida (generalmente un período de onda ), como se deriva de una descripción en las coordenadas de Lagrangian y Eulerian . La posición final en la descripción de Lagrangian se obtiene siguiendo un paquete de fluido específico durante el intervalo de tiempo. La posición final correspondiente en la descripción euleriana se obtiene al integrar la velocidad de flujo en una posición fija, igual a la posición inicial en la descripción lagrangiana, durante el mismo intervalo de tiempo.

La velocidad de deriva de Stokes es igual a la deriva de Stokes dividida por el intervalo de tiempo considerado. A menudo, la velocidad de deriva de Stokes se conoce libremente como deriva de Stokes. La deriva de Stokes puede ocurrir en todos los casos de flujo oscilatorio que no son homogéneos en el espacio. Por ejemplo en olas de agua , mareas y olas atmosféricas .

En la descripción lagrangiana , las parcelas de fluidos pueden alejarse de sus posiciones iniciales. Como resultado, la definición inequívoca de una velocidad de Lagrangiana promedio y la velocidad de deriva de Stokes, que se puede atribuir a una determinada posición fija, no es de ninguna manera una tarea trivial. Sin embargo, una descripción tan inequívoca es proporcionada por la teoría del General Lagrangiano General (GLM) de Andrews y McIntyre en 1978 . ^[2]

La deriva de Stokes es importante para la transferencia de masa de todo tipo de materiales y organismos mediante flujos oscilatorios. Además, la deriva de Stokes es importante para la generación de circulaciones de Langmuir . ^[3] Para las ondas de agua no lineales y periódicas , los resultados precisos sobre la deriva de Stokes se han calculado y tabulado.

Descripción matemática [ editar ]

El movimiento lagrangiano de una parcela de fluido con el vector de posición x = ξ ( α , t) en las coordenadas de Eulerian está dado por: ^[5]

$${\ displaystyle {\ dot {\ boldsymbol {\ xi}}} \, = \, {\ fraccion \ \ partial {\ boldsymbol {\ xi}}} {\ partial t}} \, = \, {\ boldsymbol { u}} ({\ boldsymbol {\ xi}}, t),}

donde ∂ ξ / ∂t es la derivada parcial de ξ ( α , t) con respecto a t , y

ξ ( α , t) es el vector de posición lagrangianode una parcela de fluido, en metros,

u ( x , t) es la velocidad de Euler, en metros por segundo ,

x es el vector de posición en el sistema de coordenadas de Euler , en metros,

α es el vector de posición en el sistema de coordenadas de Lagrangian , en metros,

t es el tiempo , en segundos .

A menudo, las coordenadas Lagrangianas α se eligen para coincidir con las coordenadas Eulerianas x en el tiempo inicial t = t ₀  : ^[5]

$${\ displaystyle {\ boldsymbol {\ xi}} ({\ boldsymbol {\ alpha}}, t_ {0}) \, = \, {\ boldsymbol {\ alpha}}.}

Pero también son posibles otras formas de etiquetar los paquetes de fluidos.

Si el valor promedio de una cantidad se denota por una barra, el vector de velocidad euleriana promedio ū _E y el vector de velocidad de lagrangiano promedio ū _L son:

{\ displaystyle {\ begin {alineado} {\ overline {\ boldsymbol {u}}} _ {E} \, & = \, {\ overline {{\ boldsymbol {u}} ({\ boldsymbol {x}}, t)}}, \\ {\ overline {\ boldsymbol {u}}} _ {L} \, & = \, {\ overline {{\ dot {\ boldsymbol {\ xi}}} ({\ boldsymbol {\ alpha}}, t)}} \, = \, {\ overline {\ left ({\ frac {\ partial {\ boldsymbol {\ xi}} ({\ boldsymbol {\ alpha}}, t)} {\ parcial t}} \ right)}} \, = \, {\ overline {{\ boldsymbol {u}} ({\ boldsymbol {\ xi}} ({\ boldsymbol {\ alpha}}, t), t)}} . \ end {alineado}}}

Se pueden usar diferentes definiciones del promedio , según el tema de estudio, ver teoría ergódica :

• tiempo promedio,
• media del espacio ,
• conjunto promedio y
• promedio de la fase

La velocidad de deriva de Stokes ū _S se define como la diferencia entre la velocidad euleriana media y la velocidad lagrangiana media: ^[6]

$${\ displaystyle {\ overline {\ boldsymbol {u}}} _ {S} \, = \, {\ overline {\ boldsymbol {u}}} _ {L} \, - \, {\ overline {\ boldsymbol { u}}} _ {E}.}

En muchas situaciones, el mapeo de cantidades promedio desde alguna posición euleriana xa una posición lagrangiana correspondiente α constituye un problema. Dado que una parcela fluida con la etiqueta α atraviesa una trayectoria de muchas posiciones diferentes de Eulerian x , no es posible asignar α a una única x . Una base matemáticamente sólida para un mapeo no ambiguo entre las cantidades promedio de Lagrangian y Eulerian es proporcionada por la teoría del promedio general de Lagrangian (GLM) por Andrews y McIntyre (1978) .

Ejemplo: Un flujo compresible unidimensional [ editar ]

Para la velocidad de Euler como una onda monocromática de cualquier naturaleza en un medio continuo: $${\ displaystyle u = {\ hat {u}} \ sin \ left (kx- \ omega t \ right),}Se obtiene fácilmente por la teoría de la perturbación - con$${\ displaystyle k {\ hat {u}} / \ omega} como un pequeño parámetro - para la posición de la partícula $${\ displaystyle x = \ xi (\ xi _ {0}, t):}

$${\ displaystyle {\ dot {\ xi}} = \, {u} ({\ xi}, t) = {\ hat {u}} \ sin \, \ left (k \ xi - \ omega t \ right) ,}

$${\ displaystyle \ xi (\ xi _ {0}, t) \ approx \ xi _ {0} + {\ frac {\ hat {u}} {\ omega}} \ cos (k \ xi _ {0} - \ omega t) - {\ frac {1} {4}} {\ frac {k {\ hat {u}} ^ {2}} {\ omega ^ {2}}} \ sin 2 (k \ xi _ { 0} - \ omega t) + {\ frac {1} {2}} {\ frac {k {\ hat {u}} ^ {2}} {\ omega}} t.}

Aquí el último término describe la deriva de Stokes $${\ displaystyle {\ tfrac {1} {2}} k {\ hat {u}} ^ {2} / \ omega.}^[7]

Ejemplo: olas de aguas profundas [ editar ]

Stokes deriva bajo olas periódicas en aguas profundas, durante un período T  = 5 sy una profundidad media de agua de 25 m. Izquierda : velocidades de flujo horizontal instantáneas . Derecha : velocidades de flujo promedio . Línea continua negra: velocidad euleriana media; línea discontinua roja: velocidad de Lagrangiana promedio, como se deriva de la Media de Lagrangian Generalizada (GLM).

Ver también: Teoría de la onda aerea y onda de Stokes

La deriva Stokes se formuló para las ondas de agua por George Gabriel Stokes en 1847. Por simplicidad, el caso de infinitoagua -Profunda se considera, con lineal propagación de la onda de una sinusoidalde onda en la superficie libre de una capa de fluido: ^[8]

$${\ displaystyle \ eta \, = \, a \, \ cos \, \ left (kx- \ omega t \ right),}

dónde

η es la elevación de la superficie libre en la dirección z (metros),

a es la amplitud de onda (metros),

k es el número de onda : k = 2π / λ ( radianes por metro),

ω es la frecuencia angular : ω = 2π / T ( radianes por segundo ),

x es la coordenada horizontal y la dirección de propagación de la onda (metros),

z es la coordenada vertical , con la dirección z positiva que apunta hacia afuera de la capa de fluido (metros),

λ es la longitud de onda (metros), y

T es el período de onda ( segundos ).

Como se deriva a continuación, la componente horizontal ū _S ( z ) de la velocidad de deriva de Stokes para ondas de aguas profundas es aproximadamente: ^[9]

$${\ displaystyle {\ overline {u}} _ {S} \, \ approx \, \ omega \, k \, a ^ {2} \, {\ text {e}} ^ {2kz} \, = \, {\ frac {4 \ pi ^ {2} \, a ^ {2}} {\ lambda \, T}} \, {\ text {e}} ^ {4 \ pi \, z / \ lambda}.}

Como puede verse, la velocidad de deriva Stokes ¾ _S es un no lineal cantidad en términos de la onda de amplitud una . Además, la velocidad de deriva de Stokes decae exponencialmente con la profundidad: a una profundidad de un cuarto de longitud de onda, z = -¼ λ , es aproximadamente el 4% de su valor en la superficie libre media , z = 0 .

Derivación [ editar ]

Se supone que las ondas son de amplitud infinitesimal y la superficie libre oscila alrededor del nivel medio z = 0 . Las ondas se propagan bajo la acción de la gravedad, con un vector de aceleración constante por la gravedad(apuntando hacia abajo en la dirección z negativa ). Además, se supone que el fluido es inviscido ^[10] e incompresible , con una densidad de masa constante . El flujo de fluidos es irrotacional . A profundidad infinita, el fluido se toma en reposo. .

Ahora el flujo puede representarse por un potencial de velocidad φ , que satisface la ecuación de Laplace y ^[8]

$${\ displaystyle \ varphi \, = \, {\ frac {\ omega} {k}} \, a \; {\ text {e}} ^ {kz} \, \ sin \, \ left (kx- \ omega t \ right).}

Para tener soluciones no triviales para este problema de valor propio , la longitud de la ola y el período de la olapueden no elegirse arbitrariamente, pero deben satisfacer la relación de dispersión en aguas profundas : ^[11]

$${\ displaystyle \ omega ^ {2} \, = \, g \, k.}

con g la aceleración por gravedad en ( m / s ² ). En el marco de la teoría lineal , las componentes horizontal y vertical, ξ _x y ξ _z respectivamente, de la posición de Lagrangian ξ son: ^[9]

{\ displaystyle {\ begin {alineado} \ xi _ {x} \, & = \, x \, + \, \ int \, {\ fractura \ partial \ varphi} {\ partial x}} \; {\ text {d}} t \, = \, x \, - \, a \, {\ text {e}} ^ {kz} \, \ sin \, \ left (kx- \ omega t \ right), \ \\ xi _ {z} \, & = \, z \, + \, \ int \, {\ frac {\ partial \ varphi} {\ partial z}} \; {\ text {d}} t \, = \, z \, + \, a \, {\ text {e}} ^ {kz} \, \ cos \, \ left (kx- \ omega t \ right). \ end {alineado}}}

La componente horizontal ū _S de la velocidad de deriva de Stokes se calcula utilizando una expansión de Tayloralrededor de x de la componente de velocidad horizontal euleriana u _x = ∂ξ _x / ∂t en la posición ξ  : ^[5]

${\displaystyle {\begin{aligned}{\overline {u}}_{S}\,&=\,{\overline {u_{x}({\boldsymbol {\xi }},t)}}\,-\,{\overline {u_{x}({\boldsymbol {x}},t)}}\,\\&=\,{\overline {\left[u_{x}({\boldsymbol {x}},t)\,+\,\left(\xi _{x}-x\right)\,{\frac {\partial u_{x}({\boldsymbol {x}},t)}{\partial x}}\,+\,\left(\xi _{z}-z\right)\,{\frac {\partial u_{x}({\boldsymbol {x}},t)}{\partial z}}\,+\,\cdots \right]}}-\,{\overline {u_{x}({\boldsymbol {x}},t)}}\\&\approx \,{\overline {\left(\xi _{x}-x\right)\,{\frac {\partial ^{2}\xi _{x}}{\partial x\,\partial t}}}}\,+\,{\overline {\left(\xi _{z}-z\right)\,{\frac {\partial ^{2}\xi _{x}}{\partial z\,\partial t}}}}\\&=\,{\overline {{\bigg [}-a\,{\text{e}}^{kz}\,\sin \,\left(kx-\omega t\right){\bigg ]}\,{\bigg [}-\omega \,k\,a\,{\text{e}}^{kz}\,\sin \,\left(kx-\omega t\right){\bigg ]}}}\,\\&+\,{\overline {{\bigg [}a\,{\text{e}}^{kz}\,\cos \,\left(kx-\omega t\right){\bigg ]}\,{\bigg [}\omega \,k\,a\,{\text{e}}^{kz}\,\cos \,\left(kx-\omega t\right){\bigg ]}}}\,\\&=\,{\overline {\omega \,k\,a^{2}\,{\text{e}}^{2kz}\,{\bigg [}\sin ^{2}\,\left(kx-\omega t\right)+\cos ^{2}\,\left(kx-\omega t\right){\bigg ]}}}\\&=\,\omega \,k\,a^{2}\,{\text{e}}^{2kz}.\end{aligned}}}$