SISTEMAS DE COORDENADAS

abscisa ( / æ ab s ɪ s . Ə / ; plural abscisas o abscisas o abscisas ) y el eje de ordenadas son, respectivamente, la primera y segunda coordenada de un punto en un sistema de coordenadas .

La abscisa de un punto es la medida firmada de su proyección en el eje primario, cuyo valor absoluto es la distancia entre la proyección y el origen del eje, y cuyo signo viene dado por la ubicación en la proyección relativa al origen (antes de : negativo; después: positivo).

La ordenada de un punto es la medida firmada de su proyección en el eje secundario, cuyo valor absoluto es la distancia entre la proyección y el origen del eje, y cuyo signo viene dado por la ubicación en la proyección relativa al origen (antes de : negativo; después: positivo).

Por lo general, estas son las coordenadas horizontales y verticales de un punto en un sistema de coordenadas cartesiano rectangular bidimensional . Los términos también pueden referirse a los ejes horizontal y vertical respectivamente (normalmente, el eje x y el eje y ) de un gráfico bidimensional. Un par ordenado consta de dos términos, la abscisa (horizontal, generalmente x ) y la ordenada (vertical, generalmente y ), que definen la ubicación de un punto en un espacio rectangular bidimensional.

$${\ displaystyle (\ overbrace {x} ^ {\ text {abscissa}}, \ overbrace {y} ^ {\ text {ordinate}})}

Ilustración de un plano de coordenadas cartesianas, que muestra los valores absolutos (longitudes de línea de puntos sin signo) de las coordenadas de los puntos (2, 3), (0, 0), (–3, 1) y (–1.5, –2.5) . El primer valor en cada uno de estos pares ordenados con signo es la abscisa del punto correspondiente, y el segundo valor es su ordenada.

Etimología [ editar ]

Aunque la palabra "abscisa" (en latín "linea abscisa", "una línea cortada") se ha utilizado al menos desde De Practica Geometrie publicada en 1220 por Fibonacci (Leonardo de Pisa), su uso en su sentido moderno puede deberse. al matemático veneciano Stefano degli Angeli en su obra Miscellaneum Hyperbolicum, et Parabolicumde 1659. ^[1]

En su obra de 1892, Vorlesungen über Geschichte der Mathematik, Volumen 2, (" Conferencias sobre historia de las matemáticas "), el historiador alemán Moritz Cantor escribe.

"Wir kennen keine ältere Benutzung des Wortes Abssisse en lateinischen Originalschriften [que degli Angeli de]. Vielleicht kommt das Wort en Übersetzungen der Apollonischen Kegelschnitte vor, WO Buch I Rate 20 von ἀποτεμνομέναις die ist Rede, wofür es kaum ein entsprechenderes lateinisches Wort ALS abscisa geben Möchte ". ^[2]

"No conocemos el uso anterior de la palabra abscisa en los originales en latín [que degli Angeli]. Tal vez la palabra desciende de las traducciones de las cónicas de Apolonia , donde en el Libro I, Capítulo 20 aparece ἀποτεμνομέναις, para el cual difícilmente sería tan apropiado La palabra latina como abscisa " .

En ecuaciones paramétricas [ editar ]

En una variante un tanto obsoleta, la abscisa de un punto también puede referirse a cualquier número que describa la ubicación del punto a lo largo de alguna ruta, por ejemplo, el parámetro de una ecuación paramétrica. ^[3] Usada de esta manera, la abscisa puede considerarse como un análogo de geometría de coordenadas a la variable independiente en un modelo matemático o experimento (con cualquier ordenada que cumpla una función análoga a las variables dependientes ).

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

	una	segundo	do	re	mi	F
1	a1	b1	c1	d1	e1	f1
2	a2	b2	c2	d2	e2	f2
3	a3	b3	c3	d3	e3	f3
4	a4	b4	c4	d4	e4	f4
5	a5	b5	c5	d5	e5	f5
6	a6	b6	c6	d6	e6	f6

Una cuadrícula alfanumérica (también conocida como cuadrícula de atlas ^[1] ) es un sistema de coordenadas simple en una cuadrícula en la que cada celda se identifica mediante una combinación de una letra y un número. ^[2]

Una ventaja sobre las coordenadas numéricas, que utilizan dos números en lugar de un número y una letra para referirse a una celda de cuadrícula, es que no puede haber confusión sobre qué coordenada se refiere a qué dirección. Como un ejemplo fácil, uno podría pensar en acorazado; simplemente haga coincidir el número en la parte superior con el número en la parte inferior, luego siga las dos líneas hasta que se encuentren en un punto.

La notación algebraica de ajedrez utiliza una cuadrícula alfanumérica para referirse a los cuadrados de un tablero de ajedrez.

 sistema de coordenadas baricéntrico es un sistema de coordenadas en el que la ubicación de un punto de un simplex (un triángulo, tetraedro , etc.) se especifica como el centro de masa , o baricentro, de masas generalmente desiguales colocadas en sus vértices. Las coordenadas también se extienden fuera del símplex, donde una o más coordenadas se vuelven negativas . El sistema fue introducido en 1827 por August Ferdinand Möbius .

Un 3-simplex, con subdivisiones baricéntricas de 1 cara (bordes) 2 caras (triángulos) y 3 caras (cuerpo).

Definición [ editar ]

Dejar $${\ displaystyle \ mathbf {x} _ {1}, \ ldots, \ mathbf {x} _ {n}}ser los vértices de un simplex en un espacio afín A . Si, para algun punto$${\ displaystyle \ mathbf {p}}en A ,

$${\ displaystyle (a_ {1} + \ cdots + a_ {n}) \ mathbf {p} = a_ {1} \, \ mathbf {x} _ {1} + \ cdots + a_ {n} \, \ mathbf {x} _ {n}}

y al menos uno de $${\ displaystyle a_ {1}, \ ldots, a_ {n}} no desaparece, entonces decimos que los coeficientes ($${\ displaystyle a_ {1}, \ ldots, a_ {n}}) son coordenadas baricéntricas de$${\ displaystyle \ mathbf {p}} con respecto a $${\ displaystyle \ mathbf {x} _ {1}, \ ldots, \ mathbf {x} _ {n}}. Los vértices en sí tienen las coordenadas.$${\ displaystyle \ mathbf {x} _ {1} = (1,0,0, \ ldots, 0), \ mathbf {x} _ {2} = (0,1,0, \ ldots, 0), \ ldots, \ mathbf {x} _ {n} = (0,0,0, \ ldots, 1)}. Las coordenadas baricéntricas no son únicas: para cualquier b no es igual a cero, ($${\ displaystyle ba_ {1}, \ ldots, ba_ {n}}) son también coordenadas baricéntricas de p .

Cuando las coordenadas no son negativas, el punto. $${\ displaystyle \ mathbf {p}}se encuentra en el casco convexo de$${\ displaystyle \ mathbf {x} _ {1}, \ ldots, \ mathbf {x} _ {n}}, es decir, en el simplex que tiene esos puntos como sus vértices.

Las coordenadas baricéntricas, tal como se definieron anteriormente, son una forma de coordenadas homogéneas : de hecho, las coordenadas homogéneas "usuales" son las coordenadas baricéntricas definidas en el espacio n afín extendido en el simplex cuyos vértices son los puntos en el infinito en los ejes de coordenadas, más el origen. A veces los valores de coordenadas están restringidos con una condición

$${\ displaystyle \ sum a_ {i} = 1}

lo que los hace únicos ; entonces, son coordenadas afines . La terminología clásica en este caso es la de las coordenadas baricéntricas absolutas . ^[2]

Coordenadas baricéntricas en triángulos [ editar ]

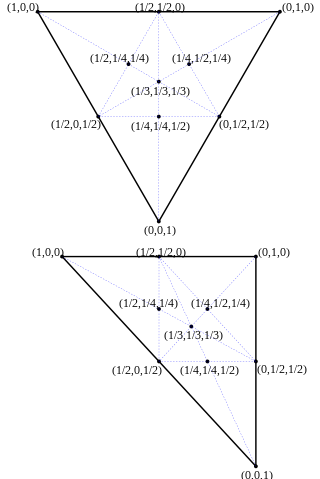
Esta sección puede ser confusa o poco clara para los lectores . En particular, es innecesariamente técnico y complicado. Por favor ayúdenos a aclarar la sección . Puede haber una discusión sobre esto en la página de discusión . ( Diciembre de 2018 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

Véase también: Ternario y centro del triángulo.

Coordenadas baricéntricas $${\ displaystyle (\ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3})} en un triángulo equilátero y en un triángulo rectángulo.

En el contexto de un triángulo , las coordenadas baricéntricas también se conocen como coordenadas de área o coordenadas de área , porque las coordenadas de P con respecto al triángulo ABC son equivalentes a las relaciones (firmadas) de las áreas de PBC , PCA y PAB al área de El triángulo de referencia ABC . Las coordenadas de área y trilineal se utilizan para propósitos similares en geometría.

Las coordenadas baricéntricas o de área son extremadamente útiles en aplicaciones de ingeniería que involucran subdominios triangulares . Esto hace que las integrales analíticas a menudo sean más fáciles de evaluar, y las tablas de cuadratura gaussianas a menudo se presentan en términos de coordenadas de área.

Considera un triangulo $${\ displaystyle T} definida por sus tres vértices, $${\ displaystyle \ mathbf {r} _ {1}}, $${\ displaystyle \ mathbf {r} _ {2}} y $${\ displaystyle \ mathbf {r} _ {3}}. Cada punto$${\ displaystyle \ mathbf {r}}ubicado dentro de este triángulo se puede escribir como una combinación convexa única de los tres vértices. En otras palabras, para cada$${\ displaystyle \ mathbf {r}} Hay una secuencia única de tres números, $${\ displaystyle \ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3} \ geq 0} tal que $${\ displaystyle \ lambda _ {1} + \ lambda _ {2} + \ lambda _ {3} = 1} y

$${\ displaystyle \ mathbf {r} = \ lambda _ {1} \ mathbf {r} _ {1} + \ lambda _ {2} \ mathbf {r} _ {2} + \ lambda _ {3} \ mathbf { r} _ {3}

Los tres numeros $${\ displaystyle \ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3}} indicar las coordenadas "baricéntricas" o "área" del punto $${\ displaystyle \ mathbf {r}}Con respecto al triángulo. A menudo se denotan como$${\ displaystyle \ alpha, \ beta, \ gamma} en lugar de $${\ displaystyle \ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3}}. Tenga en cuenta que aunque hay tres coordenadas, solo hay dos grados de libertad , ya que$${\ displaystyle \ lambda _ {1} + \ lambda _ {2} + \ lambda _ {3} = 1}. Por lo tanto, cada punto está definido de forma única por cualquiera de las dos coordenadas baricéntricas.

Para explicar por qué estas coordenadas son proporciones firmadas de áreas , asumamos que trabajamos en el espacio euclidiano$${\ displaystyle \ mathbf {E} ^ {3}}. Aquí, considere el sistema de coordenadas cartesiano $${\ displaystyle Oxyz}y su base asociada , a saber$${\ displaystyle \ {\ mathbf {i}, \ mathbf {j}, \ mathbf {k} \}}. Considera también el triángulo orientado positivamente $${\ displaystyle ABC} acostado en el $${\ displaystyle Oxy} avión . Se sabe que para cualquier base $${\ displaystyle \ {\ mathbf {e}, \ mathbf {f}, \ mathbf {g} \}} de $${\ displaystyle \ mathbf {E} ^ {3}}y cualquier vector libre $${\ displaystyle \ mathbf {h}}uno tiene ^[3]

$${\ displaystyle \ mathbf {h} = {\ frac {1} {(\ mathbf {e}, \ mathbf {f}, \ mathbf {g})}} \ cdot \ left [(\ mathbf {h}, \ mathbf {f}, \ mathbf {g}) \ mathbf {e} + (\ mathbf {e}, \ mathbf {h}, \ mathbf {g}) \ mathbf {f} + (\ mathbf {e}, \ mathbf {f}, \ mathbf {h}) \ mathbf {g} \ right],

dónde $${\ displaystyle (\ mathbf {e}, \ mathbf {f}, \ mathbf {g}) = (\ mathbf {e} \ times \ mathbf {f}) \ cdot \ mathbf {g}}representa el producto mixto de estos tres vectores.

Tomar $${\ displaystyle \ mathbf {e} = {\ vec {AB}}, \, \ mathbf {f} = {\ vec {AC}}, \, \ mathbf {g} = \ mathbf {k}, \, \ mathbf {h} = {\ vec {AP}}}, dónde $${\ displaystyle P} Es un punto arbitrario en el plano. $${\ displaystyle Oxy}, y comentar que

$${\ displaystyle (\ mathbf {e}, \ mathbf {f}, \ mathbf {h}) = ({\ vec {AB}} \ times {\ vec {AC}}) \ cdot {\ vec {AP}} = (\ vert {\ vec {AB}} \ times {\ vec {AC}} \ vert \ mathbf {k}) \ cdot {\ vec {AP}} = 0.}

Un punto sutil con respecto a nuestra elección de vectores libres: $${\ displaystyle \ mathbf {e}}Es, de hecho, la clase de equipolencia del vector enlazado. $${\ displaystyle {\ vec {AB}}}.

Hemos conseguido que

$${\ displaystyle {\ vec {AP}} = m_ {B} \ cdot {\ vec {AB}} + m_ {C} \ cdot {\ vec {AC}}, \, {\ mbox {where}} \, m_ {B} = {\ frac {({\ vec {AP}}, {\ vec {AC}}, \ mathbf {k})} {({\ vec {AB}}, {\ vec {AC}} , \ mathbf {k})}}, \, m_ {C} = {\ frac {({\ vec {AB}}, {\ vec {AP}}, \ mathbf {k})} {({\ vec {AB}}, {\ vec {AC}}, \ mathbf {k})}}.}

Dada la orientación positiva (a la izquierda ) del triángulo$${\ displaystyle ABC}, el denominador de ambos$${\ displaystyle m_ {B}} y $${\ displaystyle m_ {C}}Es precisamente el doble del área del triángulo. $${\ displaystyle ABC}. También,

$${\ displaystyle ({\ vec {AP}}, {\ vec {AC}}, \ mathbf {k}) = ({\ vec {PC}}, {\ vec {PA}}, \ mathbf {k}) \, {\ mbox {y}} \, ({\ vec {AB}}, {\ vec {AP}}, \ mathbf {k}) = ({\ vec {PA}}, {\ vec {PB} }, \ mathbf {k})}

y así los numeradores de$${\ displaystyle m_ {B}} y $${\ displaystyle m_ {C}}Son los dobles de las áreas firmadas de triángulos.$${\ displaystyle APC} y respectivamente $${\ displaystyle ABP}.

Además, deducimos que

$${\ displaystyle {\ vec {OP}} = (1-m_ {B} -m_ {C}) \ cdot {\ vec {OA}} + m_ {B} \ cdot {\ vec {OB}} + m_ { C} \ cdot {\ vec {OC}}}

lo que significa que los números $${\ displaystyle 1-m_ {B} -m_ {C}}, $${\ displaystyle m_ {B}} y $${\ displaystyle m_ {C}} son las coordenadas baricéntricas de $${\ displaystyle P}. Del mismo modo, la tercera coordenada baricéntrica se lee como

$${\ displaystyle m_ {A} = 1-m_ {B} -m_ {C} = {\ frac {({\ vec {PB}}, {\ vec {PC}}, \ mathbf {k})} {( {\ vec {AB}}, {\ vec {AC}}, \ mathbf {k})}}.}

Esta $${\ displaystyle m}La notación de boletín de las coordenadas baricéntricas proviene del hecho de que el punto $${\ displaystyle P}Puede ser interpretado como el centro de masa para las masas.$${\ displaystyle m_ {A}}, $${\ displaystyle m_ {B}}, $${\ displaystyle m_ {C}} que se encuentran en $${\ displaystyle A}, $${\ displaystyle B} y $${\ displaystyle C}.

Cambiar de un lado a otro entre las coordenadas baricéntricas y otros sistemas de coordenadas hace que algunos problemas sean mucho más fáciles de resolver.

Conversión entre coordenadas baricéntricas y cartesianas [ editar ]

Dado un punto $${\ displaystyle \ mathbf {r}} en el plano de un triángulo se pueden obtener las coordenadas baricéntricas $${\ displaystyle \ lambda _ {1}}, $${\ displaystyle \ lambda _ {2}} y $${\ displaystyle \ lambda _ {3}}De las coordenadas cartesianas. $${\ displaystyle (x, y)} o viceversa.

Podemos escribir las coordenadas cartesianas del punto. $${\ displaystyle \ mathbf {r}} en términos de los componentes cartesianos de los vértices de triángulos $${\ displaystyle \ mathbf {r} _ {1}}, $${\ displaystyle \ mathbf {r} _ {2}}, $${\ displaystyle \ mathbf {r} _ {3}} dónde $${\ displaystyle \ mathbf {r} _ {i} = (x_ {i}, y_ {i})} y en términos de las coordenadas baricéntricas de $${\ displaystyle \ mathbf {r}} como

$${\ displaystyle {\ begin {matrix} x = \ lambda _ {1} x_ {1} + \ lambda _ {2} x_ {2} + \ lambda _ {3} x_ {3} \\ y = = lambda _ {1} y_ {1} + \ lambda _ {2} y_ {2} + \ lambda _ {3} y_ {3} \\\ fin {matriz}}}

Es decir, las coordenadas cartesianas de cualquier punto son un promedio ponderado de las coordenadas cartesianas de los vértices del triángulo, y los pesos son las coordenadas baricéntricas del punto que se suman a la unidad.

Para encontrar la transformación inversa, de coordenadas cartesianas a coordenadas baricéntricas, primero sustituimos $${\ displaystyle \ lambda _ {3} = 1- \ lambda _ {1} - \ lambda _ {2}} en lo anterior para obtener

$${\ displaystyle {\ begin {matrix} x = \ lambda _ {1} x_ {1} + \ lambda _ {2} x_ {2} + (1- \ lambda _ {1} - \ lambda _ {2}) x_ {3} \\ y = \ lambda _ {1} y_ {1} + \ lambda _ {2} y_ {2} + (1- \ lambda _ {1} - \ lambda _ {2}) y_ {3 } \\\ fin {matriz}}}

Reorganizando, esto es

$${\ displaystyle {\ begin {matrix} \ lambda _ {1} (x_ {1} -x_ {3}) + \ lambda _ {2} (x_ {2} -x_ {3}) + x_ {3} - x = 0 \\\ lambda _ {1} (y_ {1} -y_ {3}) + \ lambda _ {2} (y_ {2} -y_ {3}) + y_ {3} -y = 0 \ \\ fin {matriz}}}

Esta transformación lineal puede escribirse más sucintamente como

$${\ displaystyle \ mathbf {T} \ cdot \ lambda = \ mathbf {r} - \ mathbf {r} _ {3}}

dónde $${\ displaystyle \ lambda}es el vector de las dos primeras coordenadas baricéntricas,$${\ displaystyle \ mathbf {r}}es el vector de coordenadas cartesianas , y$${\ displaystyle \ mathbf {T}}es una matriz dada por

{\ displaystyle \ mathbf {T} = \ left ({\ begin {matrix} x_ {1} -x_ {3} & x_ {2} -x_ {3} \\ y_ {1} -y_ {3} & y_ {2 } -y_ {3} \\\ fin {matriz}} \ derecha)}

Ahora la matriz $${\ displaystyle \ mathbf {T}}es invertible , ya que$${\ displaystyle \ mathbf {r} _ {1} - \ mathbf {r} _ {3}} y $${\ displaystyle \ mathbf {r} _ {2} - \ mathbf {r} _ {3}}son linealmente independientes (si este no fuera el caso, entonces$${\ displaystyle \ mathbf {r} _ {1}}, $${\ displaystyle \ mathbf {r} _ {2}}y $${\ displaystyle \ mathbf {r} _ {3}}sería colineal y no formaría un triángulo). Por lo tanto, podemos reorganizar la ecuación anterior para obtener

$${\ displaystyle \ left ({\ begin {matrix} \ lambda _ {1} \\\ lambda _ {2} \ end {matrix}} \ right) = \ mathbf {T} ^ {- 1} (\ mathbf { r} - \ mathbf {r} _ {3})}

Encontrar las coordenadas baricéntricas se ha reducido así a encontrar la matriz inversa 2 × 2 de$${\ displaystyle \ mathbf {T}}, un problema fácil.

Explícitamente, las fórmulas para las coordenadas baricéntricas del punto. $${\ displaystyle \ mathbf {r}}en términos de sus coordenadas cartesianas ( x, y ) y en términos de las coordenadas cartesianas de los vértices del triángulo son:

$${\ displaystyle \ lambda _ {1} = {\ frac {(y_ {2} -y_ {3}) (x-x_ {3}) + (x_ {3} -x_ {2}) (y-y_ { 3})} {\ det (T)}} = {\ frac {(y_ {2} -y_ {3}) (x-x_ {3}) + (x_ {3} -x_ {2}) (y -y_ {3})} {(y_ {2} -y_ {3}) (x_ {1} -x_ {3}) + (x_ {3} -x_ {2}) (y_ {1} -y_ { 3})}} \ ,,}

$${\ displaystyle \ lambda _ {2} = {\ frac {(y_ {3} -y_ {1}) (x-x_ {3}) + (x_ {1} -x_ {3}) (y-y_ { 3})} {\ det (T)}} = {\ frac {(y_ {3} -y_ {1}) (x-x_ {3}) + (x_ {1} -x_ {3}) (y -y_ {3})} {(y_ {2} -y_ {3}) (x_ {1} -x_ {3}) + (x_ {3} -x_ {2}) (y_ {1} -y_ { 3})}} \ ,,}

$${\ displaystyle \ lambda _ {3} = 1- \ lambda _ {1} - \ lambda _ {2} \ ,.}

Otra forma de resolver la conversión de coordenadas cartesianas a baricéntricas es reescribir el problema en forma matricial para que

$${\ displaystyle \ mathbf {r} = \ mathbf {R} {\ boldsymbol {\ lambda}}}

con $${\ displaystyle \ mathbf {R} = \ left ({\ begin {matrix} \ mathbf {r} _ {1} | \ mathbf {r} _ {2} | \ mathbf {r} _ {3} \ end { matriz}} \ derecha)} y $${\ displaystyle {\ boldsymbol {\ lambda}} = \ left (\ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3} \ right) ^ {\ top}}. Entonces, la condición$${\ displaystyle \ lambda _ {1} + \ lambda _ {2} + \ lambda _ {3} = 1} lee $${\ displaystyle \ left (1,1,1 \ right) {\ boldsymbol {\ lambda}} = 1} y las coordenadas baricéntricas se pueden resolver como la solución del sistema lineal

{\ displaystyle \ left ({\ begin {matrix} x_ {1} & x_ {2} & x_ {3} \\ y_ {1} & y_ {2} & y_ {3} \\ 1 & 1 & 1 \ end {matrix}} \ right) {\ boldsymbol {\ lambda}} = \ left ({\ begin {matrix} x \\ y \\ 1 \ end {matrix}} \ right)}

Conversión entre coordenadas baricéntricas y trilineales [ editar ]

Un punto con coordenadas trilineales x  : y  : z tiene coordenadas baricéntricas ax  : by  : cz donde a , b , c son las longitudes laterales del triángulo. A la inversa, un punto con baricéntricos.$${\ displaystyle \ lambda _ {1}: \ lambda _ {2}: \ lambda _ {3}} tiene trilinear $${\ displaystyle \ lambda _ {1} / a: \ lambda _ {2} / b: \ lambda _ {3} / c.}

Ecuaciones en coordenadas baricéntricas [ editar ]

Los lados a, b, c respectivamente tienen ecuaciones ^[4]

$${\ displaystyle \ lambda _ {1} = 0, \ quad \ lambda _ {2} = 0, \ quad \ lambda _ {3} = 0.}

La ecuación de la línea de Euler de un triángulo es ^[4]

{\ displaystyle {\ begin {vmatrix} \ lambda _ {1} & \ lambda _ {2} & \ lambda _ {3} \\ 1 & 1 & 1 \\\ tan A & \ tan B & \ tan C \ end {vmatrix}} = 0.}

Usando la conversión dada previamente entre coordenadas baricéntricas y trilineales, las otras varias ecuaciones dadas en las coordenadas trilineales # Las fórmulas se pueden reescribir en términos de coordenadas baricéntricas.

Distancia entre puntos [ editar ]

El vector de desplazamiento de dos puntos normalizados. $${\ displaystyle P = (p_ {1}, p_ {2}, p_ {3})} y $${\ displaystyle Q = (q_ {1}, q_ {2}, q_ {3})}es ^[5]

$${\ displaystyle {\ overrightarrow {PQ}} = (p_ {1} -q_ {1}, p_ {2} -q_ {2}, p_ {3} -q_ {3}).}

La distancia $${\ displaystyle d} Entre $${\ displaystyle P} y $${\ displaystyle Q}, o la longitud del vector de desplazamiento $${\ displaystyle {\ overrightarrow {PQ}} = (x, y, z),}es ^[4] [5]

$${\ displaystyle d ^ {2} = \ left | PQ \ right | ^ {2} = - a ^ {2} yz-b ^ {2} zx-c ^ {2} xy = {\ frac {1} { 2}} [x ^ {2} (b ^ {2} + c ^ {2} -a ^ {2}) + y ^ {2} (c ^ {2} + a ^ {2} -b ^ { 2}) + z ^ {2} (a ^ {2} + b ^ {2} -c ^ {2})].}

donde a, b, c son las longitudes laterales del triángulo. La equivalencia de las dos últimas expresiones se deduce de$${\ displaystyle x + y + z = 0,} que sostiene porque $${\ displaystyle x + y + z = (p_ {1} -q_ {1}) + (p_ {2} -q_ {2}) + (p_ {3} -q_ {3}) = (p_ {1} + p_ {2} + p_ {3}) - (q_ {1} + q_ {2} + q_ {3}) = 1-1 = 0.}

Las coordenadas baricéntricas de un punto se pueden calcular basándose en las distancias d _i a los tres vértices de triángulos resolviendo la ecuación

{\ displaystyle \ left ({\ begin {matrix} -c ^ {2} & c ^ {2} & b ^ {2} -a ^ {2} \\ - b ^ {2} & c ^ {2} -a ^ {2} & b ^ {2} \\ 1 & 1 & 1 \ end {matrix}} \ right) {\ boldsymbol {\ lambda}} = \ left ({\ begin {matrix} d_ {A} ^ {2} -d_ {B } ^ {2} \\ d_ {A} ^ {2} -d_ {C} ^ {2} \\ 1 \ end {matriz}} \ derecha).}

Aplicaciones [ editar ]

Determinación de la ubicación con respecto a un triángulo [ editar ]

Aunque las coordenadas baricéntricas se usan más comúnmente para manejar puntos dentro de un triángulo, también se pueden usar para describir un punto fuera del triángulo. Si el punto no está dentro del triángulo, aún podemos usar las fórmulas anteriores para calcular las coordenadas baricéntricas. Sin embargo, dado que el punto está fuera del triángulo, al menos una de las coordenadas violará nuestra suposición original de que$${\ displaystyle \ lambda _ {1 ... 3} \ geq 0}. De hecho, dado cualquier punto en las coordenadas cartesianas, podemos usar este hecho para determinar dónde se encuentra este punto con respecto a un triángulo.

Si un punto se encuentra en el interior del triángulo, todas las coordenadas baricéntricas se encuentran en el intervalo abierto $${\ displaystyle (0,1).} Si un punto se encuentra en un borde del triángulo pero no en un vértice, una de las coordenadas de área $${\ displaystyle \ lambda _ {1 ... 3}} (el asociado con el vértice opuesto) es cero, mientras que los otros dos se encuentran en el intervalo abierto $${\ displaystyle (0,1).}Si el punto se encuentra en un vértice, la coordenada asociada con ese vértice es igual a 1 y el resto es igual a cero. Finalmente, si el punto se encuentra fuera del triángulo, al menos una coordenada es negativa.

Resumiendo,

Punto $${\ displaystyle \ mathbf {r}}se encuentra dentro del triángulo si y solo si {\ displaystyle 0 <\ lambda _ {i} <1 font="" forall="" i="" in="" text="">.

$${\ displaystyle \ mathbf {r}} se encuentra en el borde o esquina del triángulo si $${\ displaystyle 0 \ leq \ lambda _ {i} \ leq 1 \; \ forall \; i {\ text {in}} {1,2,3}} y $${\ displaystyle \ lambda _ {i} = 0 \; {\ text {, para algunos i in}} {1,2,3}}.

De otra manera, $${\ displaystyle \ mathbf {r}} se encuentra fuera del triángulo.

En particular, si un punto se encuentra en el lado opuesto de una línea lateral desde el vértice opuesto a esa línea lateral, entonces la coordenada baricéntrica de ese punto correspondiente a ese vértice es negativa.

Interpolación en una rejilla triangular no estructurada [ editar ]

Superficie (parte superior) obtenida de la interpolación lineal sobre una cuadrícula triangular dada (parte inferior) en el plano x , y . La superficie se aproxima a una función z = f ( x , y ), dados solo los valores de f en los vértices de la cuadrícula.

Si $${\ displaystyle f (\ mathbf {r} _ {1}), f (\ mathbf {r} _ {2}), f (\ mathbf {r} _ {3})} Se conocen cantidades, pero los valores de $${\ displaystyle f} dentro del triangulo definido por $${\ displaystyle \ mathbf {r} _ {1}, \ mathbf {r} _ {2}, \ mathbf {r} _ {3}}Se desconoce, se pueden aproximar mediante interpolación lineal . Las coordenadas baricéntricas proporcionan una forma conveniente de calcular esta interpolación. Si$${\ displaystyle \ mathbf {r}} Es un punto dentro del triángulo con coordenadas baricéntricas. $${\ displaystyle \ lambda _ {1}}, $${\ displaystyle \ lambda _ {2}}, $${\ displaystyle \ lambda _ {3}}, entonces

$${\ displaystyle f (\ mathbf {r}) \ approx \ lambda _ {1} f (\ mathbf {r} _ {1}) + \ lambda _ {2} f (\ mathbf {r} _ {2}) + \ lambda _ {3} f (\ mathbf {r} _ {3})}

En general, dada cualquier cuadrícula no estructurada o malla poligonal , este tipo de técnica puede utilizarse para aproximar el valor de$${\ displaystyle f}en todos los puntos, siempre que el valor de la función sea conocido en todos los vértices de la malla. En este caso, tenemos muchos triángulos, cada uno correspondiente a una parte diferente del espacio. Interpolar una función.$${\ displaystyle f} en un punto $${\ displaystyle \ mathbf {r}}, primero se debe encontrar un triángulo que contenga $${\ displaystyle \ mathbf {r}}. Para hacerlo$${\ displaystyle \ mathbf {r}}Se transforma en las coordenadas baricéntricas de cada triángulo. Si se encuentra algún triángulo tal que las coordenadas satisfacen$${\ displaystyle 0 \ leq \ lambda _ {i} \ leq 1 \; \ forall \; i {\ text {in}} 1,2,3}, entonces el punto se encuentra en ese triángulo o en su borde (explicado en la sección anterior). Entonces el valor de$${\ displaystyle f (\ mathbf {r})} Se puede interpolar como se describe anteriormente.

Estos métodos tienen muchas aplicaciones, como el método de elementos finitos (FEM).

Integración sobre un triángulo [ editar ]

La integral de una función sobre el dominio del triángulo puede ser molesta para calcular en un sistema de coordenadas cartesiano. Generalmente, uno tiene que dividir el triángulo en dos mitades, y le sigue un gran desorden. En cambio, a menudo es más fácil hacer un cambio de variables a cualquiera de las dos coordenadas baricéntricas, por ejemplo,$${\ displaystyle \ lambda _ {1}, \ lambda _ {2}}. Bajo este cambio de variables,

$${\ displaystyle \ int _ {T} f (\ mathbf {r}) \ d \ mathbf {r} = 2A \ int _ {0} ^ {1} \ int _ {0} ^ {1- \ lambda _ { 2}} f (\ lambda _ {1} \ mathbf {r} _ {1} + \ lambda _ {2} \ mathbf {r} _ {2} + (1- \ lambda _ {1} - \ lambda _ {2}) \ mathbf {r} _ {3}) \ d \ lambda _ {1} \ d \ lambda _ {2}}

dónde $${\ displaystyle A}Es el área del triángulo. Este resultado se deriva del hecho de que un rectángulo en coordenadas baricéntricas corresponde a un cuadrilátero en coordenadas cartesianas, y la proporción de las áreas de las formas correspondientes en los sistemas de coordenadas correspondientes viene dada por$${\ displaystyle 2A}.

Ejemplos de puntos especiales [ editar ]

Los tres vértices de un triángulo tienen coordenadas baricéntricas$${\ displaystyle 1: 0: 0, \ quad 0: 1: 0, \ quad {\ text {y}} \ quad 0: 0: 1.}^[4]

El centroide tiene baricéntricos.$${\ displaystyle 1: 1: 1.}^[4]

El circuncentro de un triángulo ABC tiene coordenadas baricéntricas ^{[4] [5] [6] [7]}

$${\ displaystyle a ^ {2} (- a ^ {2} + b ^ {2} + c ^ {2}): \; b ^ {2} (a ^ {2} -b ^ {2} + c ^ {2}): \; c ^ {2} (a ^ {2} + b ^ {2} -c ^ {2})}

$${\ displaystyle = \ sin 2A: \ sin 2B: \ sin 2C = (1- \ cos B \ cos C) :( 1- \ cos C \ cos A) :( 1- \ cos A \ cos B).}

donde a , b , c son longitudes de borde BC , CA , AB respectivamente del triángulo.

El ortocentro tiene coordenadas baricéntricas ^[4] [5]

$${\ displaystyle (a ^ {2} + b ^ {2} -c ^ {2}) (a ^ {2} -b ^ {2} + c ^ {2}): \; (- a ^ {2 } + b ^ {2} + c ^ {2}) (a ^ {2} + b ^ {2} -c ^ {2}): \; (a ^ {2} -b ^ {2} + c ^ {2}) (- a ^ {2} + b ^ {2} + c ^ {2})}

$${\ displaystyle = \ tan A: \ tan B: \ tan C = a \ cos B \ cos C: b \ cos C \ cos A: c \ cos A \ cos B.}

El incentivo tiene coordenadas baricéntricas ^[5] [8]

$${\ displaystyle a: b: c = \ sin A: \ sin B: \ sin C.}

Los baricéntricos de los excéntricos son ^[8]

$${\ displaystyle -a: b: c \ quad \ quad a: -b: c \ quad \ quad a: b: -c.}

El centro de nueve puntos tiene coordenadas baricéntricas ^[4] [8]

$${\ displaystyle a \ cos (BC): b \ cos (CA): c \ cos (AB) = (1+ \ cos B \ cos C) :( 1+ \ cos C \ cos A) :( 1+ \ cos A \ cos B)}

$${\ displaystyle = [a ^ {2} (b ^ {2} + c ^ {2}) - (b ^ {2} -c ^ {2}) ^ {2}]: [b ^ {2} ( c ^ {2} + a ^ {2}) - (c ^ {2} -a ^ {2}) ^ {2}]: [c ^ {2} (a ^ {2} + b ^ {2} ) - (a ^ {2} -b ^ {2}) ^ {2}].}

Coordenadas baricéntricas en tetraedros [ editar ]

Las coordenadas baricéntricas se pueden extender fácilmente a tres dimensiones . El simplex 3D es un tetraedro, un poliedro que tiene cuatro caras triangulares y cuatro vértices. Una vez más, las coordenadas baricéntricas se definen de manera que el primer vértice$${\ displaystyle \ mathbf {r} _ {1}} mapas de coordenadas baricéntricos $${\ displaystyle \ lambda = (1,0,0,0)}, $${\ displaystyle \ mathbf {r} _ {2} \ a (0,1,0,0)}, etc.

Esto es nuevamente una transformación lineal, y podemos extender el procedimiento anterior para que los triángulos encuentren las coordenadas baricéntricas de un punto $${\ displaystyle \ mathbf {r}} Con respecto a un tetraedro:

$${\ displaystyle \ left ({\ begin {matrix} \ lambda _ {1} \\\ lambda _ {2} \\\ lambda _ {3} \ end {matrix}} \ right) = \ mathbf {T} ^ {-1} (\ mathbf {r} - \ mathbf {r} _ {4})}

dónde $${\ displaystyle \ mathbf {T}} Ahora es una matriz de 3 × 3:

{\ displaystyle \ mathbf {T} = \ left ({\ begin {matrix} x_ {1} -x_ {4} & x_ {2} -x_ {4} & x_ {3} -x_ {4} \\ y_ {1 } -y_ {4} & y_ {2} -y_ {4} & y_ {3} -y_ {4} \\ z_ {1} -z_ {4} & z_ {2} -z_ {4} & z_ {3} -z_ {4} \ end {matrix}} \ right)}

Una vez más, el problema de encontrar las coordenadas baricéntricas se ha reducido a invertir una matriz de 3 × 3. Las coordenadas baricéntricas 3D se pueden usar para decidir si un punto se encuentra dentro de un volumen tetraédrico y para interpolar una función dentro de una malla tetraédrica, de manera análoga al procedimiento 2D. Las mallas tetraédricas se usan a menudo en el análisis de elementos finitos porque el uso de coordenadas baricéntricas puede simplificar enormemente la interpolación 3D.

Coordenadas baricéntricas generalizadas [ editar ]

Esta sección no cita ninguna fuente . Por favor, ayuda a mejorar esta sección mediante la adición de citas de fuentes confiables . El material sin fuente puede ser cuestionado y eliminado . ( Diciembre de 2010 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

Las coordenadas baricéntricas ( a ₁ , ..., a _n ) que se definen con respecto a un politopo en lugar de un simplex se denominan coordenadas baricéntricas generalizadas . Para estos, la ecuación.

$${\ displaystyle (a_ {1} + \ cdots + a_ {n}) p = a_ {1} x_ {1} + \ cdots + a_ {n} x_ {n}}

aún es necesario mantener donde x ₁ , ..., x _n son los vértices del politopo dado. Por lo tanto, la definición no se modifica formalmente, pero mientras que un símplex con n vértices debe incrustarse en un espacio vectorial de dimensión de al menos n-1 , un politopo puede incrustarse en un espacio vectorial de dimensión inferior. El ejemplo más simple es un cuadrilátero en el plano. En consecuencia, incluso las coordenadas baricéntricas generalizadas normalizadas (es decir, las coordenadas tales que la suma de los coeficientes es 1) en general ya no se determinan de forma única, mientras que este es el caso de las coordenadas baricéntricas normalizadas con respecto a un simplex.

Más abstractamente, las coordenadas baricéntricas generalizadas expresan un politopo con n vértices, independientemente de la dimensión, como la imagen del estándar.$${\ displaystyle (n-1)}-simplex, que tiene n vértices - el mapa está en:$${\ displaystyle \ Delta ^ {n-1} \ twoheadrightarrowarrow P.}El mapa es uno a uno si y solo si el politopo es un símplex, en cuyo caso el mapa es un isomorfismo; esto corresponde a un punto que no tiene coordenadas baricéntricas generalizadas únicas,excepto cuando P es un simplex.

Las coordenadas baricéntricas de doble a generalizadas son variables de holgura , que miden la cantidad de margen que un punto satisface las restricciones lineales y proporciona una incorporación $${\ displaystyle P \ hookrightarrow (\ mathbf {R} _ {\ geq 0}) ^ {f}}en la f - ortante , donde f es el número de caras (dual a los vértices). Este mapa es uno a uno (las variables de holgura se determinan únicamente) pero no en (no se pueden realizar todas las combinaciones).

Este uso de la norma. $${\ displaystyle (n-1)}-simplex y f -stántalos como objetos estándar que se asignan a un politopo o que un politopo se asigna deben contrastarse con el uso del espacio vectorial estándar$${\ displaystyle K ^ {n}}como el objeto estándar para espacios vectoriales, y el hiperplano afín estándar $${\ displaystyle \ {(x_ {0}, \ ldots, x_ {n}) \ mid \ sum x_ {i} = 1 \} \ subset K ^ {n + 1}}como el objeto estándar para espacios afines, donde en cada caso la elección de una base lineal o afín proporciona un isomorfismo, permitiendo que todos los espacios vectoriales y espacios afines se consideren en términos de estos espacios estándar, en lugar de uno hacia o uno a uno un mapa (no todo politopo es un simplex). Además, el símbolo n es el objeto estándar que se asigna a los conos.

Aplicaciones [ editar ]

Las coordenadas baricéntricas generalizadas tienen aplicaciones en gráficos de computadora y más específicamente en modelado geométrico . A menudo, un poliedro puede aproximar un modelo tridimensional de modo que las coordenadas baricéntricas generalizadas con respecto a ese poliedro tengan un significado geométrico. De esta manera, el procesamiento del modelo se puede simplificar utilizando estas coordenadas significativas. Las coordenadas baricéntricas también se utilizan en geofísica ^[9]