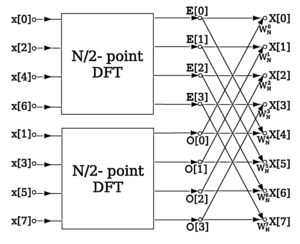
En el contexto de los algoritmos rápidos de transformación de Fourier , una mariposa es una parte del cálculo que combina los resultados de transformadas de Fourier discretas (DFT) más pequeñas en una DFT más grande, o viceversa (dividiendo una DFT más grande en subtransformas). El nombre "mariposa" proviene de la forma del diagrama de flujo de datos en el caso de radix-2, como se describe a continuación. [1] Se cree que la primera aparición impresa del término se encuentra en un informe técnico de 1969 del MIT . [2] [3] La misma estructura también se puede encontrar en el algoritmo de Viterbi , utilizado para encontrar la secuencia más probable de estados ocultos.
Más comúnmente, el término "mariposa" aparece en el contexto del algoritmo FFT de Cooley-Tukey , que desglosa recursivamente una DFT de tamaño compuesto n = rm en r transformaciones más pequeñas de tamaño m donde r es el "radix" de la transformada. Estas DFT más pequeñas se combinan a través de mariposas de tamaño r , que a su vez son DFT de tamaño r (realizadas m veces en las salidas correspondientes de las sub-transformadas) previamente multiplicadas por raíces de unidad (conocidas como factores de twiddle). (Este es el caso "decimación en el tiempo"; también se puede realizar los pasos a la inversa, conocidos como "decimación en frecuencia", donde las mariposas vienen primero y son-post multiplicado por factores de rotación Véase también el. Cooley-Tukey FFTartículo .)
Diagrama de mariposa Radix-2 [ editar ]
En el caso del algoritmo radix-2 Cooley-Tukey, la mariposa es simplemente una DFT de tamaño-2 que toma dos entradas ( x 0 , x 1 ) (salidas correspondientes de las dos sub-transformadas) y da dos salidas ( y 0 , y 1 ) por la fórmula (sin incluir los factores de twiddle ):
Si uno dibuja el diagrama de flujo de datos para este par de operaciones, las líneas ( x 0 , x 1 ) a ( y 0 , y 1 ) se cruzan y se parecen a las alas de una mariposa , de ahí el nombre (vea también la ilustración de la derecha) ).
Más específicamente, un algoritmo FFT de diezmado en el tiempo de radix-2 en n = 2 p entradas con respecto a una n-ª raíz primitiva de la unidad Se basa en O ( n log n ) mariposas de la forma:
donde k es un número entero dependiendo de la parte de la transformación que se calcula. Mientras que la transformación inversa correspondiente se puede realizar matemáticamente reemplazando ω con ω −1 (y posiblemente multiplicando por un factor de escala global, dependiendo de la convención de normalización), también se puede invertir directamente las mariposas:
Correspondiente a un algoritmo de FFT de decimación en frecuencia.
Otros usos [ editar ]
La mariposa también se puede usar para mejorar la aleatoriedad de grandes conjuntos de números parcialmente aleatorios, al poner cada palabra de 32 o 64 bits en contacto causal con cualquier otra palabra a través de un algoritmo de hashing deseado, para que un cambio en cualquier bit tenga la posibilidad de cambiar todos los bits en la gran matriz.
Un diagrama de Carroll , plaza de Lewis Carroll , diagrama biliteral o una tabla de doble entrada es un diagrama utilizado para agrupar cosas de un sí / no de la moda. Los números u objetos se clasifican como 'x' (que tienen un atributo x) o 'no x' (que no tienen un atributo 'x'). Llevan el nombre de Lewis Carroll , el seudónimo de Charles Lutwidge Dodgson .
Uso [ editar ]
Aunque los diagramas de Carroll pueden ser tan simples como el primero de arriba, los tipos más conocidos son aquellos similares al segundo, donde se muestran dos atributos. El 'universo' de un diagrama de Carroll está contenido dentro de los cuadros en el diagrama, ya que cualquier número u objeto debe tener un atributo o no tenerlo.
Los escolares aprenden con frecuencia los diagramas de Carroll , pero también pueden usarse fuera del campo de la educación , ya que son una forma ordenada de categorizar y mostrar información.
Un cartograma es un mapa en el que alguna variable de mapeo temático, como el tiempo de viaje, la población o el PNB , se sustituye por el área terrestre o la distancia. La geometría o el espacio del mapa está distorsionado, a veces extremadamente, para transmitir la información de esta variable alternativa. Se utilizan principalmente para mostrar el énfasis y para el análisis como nomografías . [1]
Dos tipos comunes de cartogramas son los cartogramas de área y distancia. Los cartogramas tienen una historia bastante larga, con ejemplos de mediados del siglo XIX.
Cartogramas de área [ editar ]
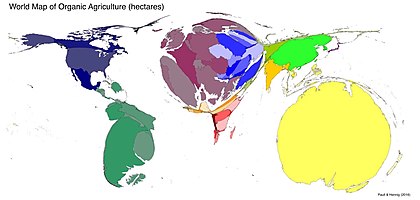
Un cartograma de área a veces se conoce como un mapa de valor por área o un mapa isodemográfico , este último particularmente para un cartograma de población , que ilustra los tamaños relativos de las poblaciones de los países del mundo al escalar el área de cada país en proporcional a su población; La forma y la ubicación relativa de cada país se mantienen en la mayor medida posible, pero inevitablemente se produce una gran cantidad de distorsión. Otros sinónimos en uso son mapa anamórfico , mapa de densidad de compensación y mapa Gastner . [4] [5] [6]
Los cartogramas de área pueden ser contiguos o no contiguos. Los cartogramas de área que se muestran en esta página son todos contiguos, mientras que un buen ejemplo de un cartograma no contiguo se publicó en The New York Times . [7] [8] Este método de creación de cartogram a veces se conoce como el método del proyector o regiones reducidas .
Los cartogramas pueden clasificarse también por las propiedades de la forma y la preservación de la topología. Los cartogramas de área clásica (que se muestran en esta página) típicamente distorsionan la forma de las unidades espaciales hasta cierto punto, pero son estrictos para preservar las relaciones de vecindad correctas entre ellos. Los cartogramas reducidos (del ejemplo de NY Times) son estrictamente conservadores de formas. Otra rama de cartogramas introducida por Dorling, reemplaza las formas reales con círculos escalados de acuerdo con la característica asignada. Los círculos se distribuyen para parecerse a la topología original. El cartograma de Demers es una variación del cartograma de Dorling, pero utiliza rectángulos en lugar de círculos, e intenta retener señales visuales a expensas de la distancia mínima. Los mapas esquemáticos basados en árboles cuádruples se pueden ver como cartogramas que no preservan la forma con cierto grado de preservación del vecindario.
Una colección de cartogramas de área contigua está disponible en Worldmapper, [9] que fue iniciada por un equipo colaborativo de investigadores de las Universidades de Sheffield y Michigan .
Producción [ editar ]
Uno de los primeros cartógrafos en generar cartogramas con la ayuda de visualización por computadora fue Waldo Tobler de UC Santa Barbara en la década de 1960. Antes del trabajo de Tobler, los cartogramas se creaban a mano (como en ocasiones todavía lo son). El Centro Nacional de Información y Análisis Geográficos ubicado en el campus de UCSB mantiene un Centro Central de Cartogramas en línea con recursos relacionados con los cartogramas.
Una serie de paquetes de software generan cartogramas. La mayoría de las herramientas de generación de cartogramas disponibles trabajan en conjunto con otras herramientas de software GIS como complementos o producen resultados cartográficos de datos GIS formateados para trabajar con productos GIS de uso común. Ejemplos de software incluyen cartograma ScapeToad, [10] [11] de la compra, [12] y la herramienta de procesamiento Cartograma (un ArcScript para ESRI 's ArcGIS ), que todos utilizan el algoritmo Gastner-Newman. [13] [14] Un algoritmo alternativo, Carto3F, [15] también se implementa como un programa independiente para uso no comercial en plataformas Windows. [dieciséis]Este programa también proporciona una optimización para el algoritmo original de hoja de goma Dougenik. [17] [18] El paquete de mapas CRAN proporciona una implementación de un algoritmo de cartograma rectangular. [19]
Los cartogramas también se pueden construir manualmente, ya sea a mano o en un entorno asistido por computadora. Los cartogramas de bloques se construyen organizando bloques de igual tamaño geométricamente regulares, con el número de bloques asignados a cada distrito proporcional a la variable de población. Varios ejemplos de cartogramas bloques fueron publicados durante la temporada de elecciones presidenciales de Estados Unidos 2016 por The Washington Post , [20] el FiveThirtyEight blog, [21] y el Wall Street Journal , [22] entre otros.
Algoritmos [ editar ]
Esta tabla incluye una lista de referencias , lectura relacionada o enlaces externos , pero sus fuentes no están claras porque carecen de citas en línea . ( Noviembre de 2014 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )
|
| Año | Autor | Algoritmo | Tipo | Preservación de la forma | Preservación de la topología |
|---|---|---|---|---|---|
| 1973 | Tobler | Método de mapa de goma | área contigua | con distorsión | Sí, pero no garantizado |
| 1976 | Olson | Metodo de proyector | área no contigua | sí | No |
| 1978 | Kadmon, Shlomi | Proyección polifocal | distancia radial | Desconocido | Desconocido |
| 1984 | Selvin et al. | Método DEMP (Expansión Radial) | área contigua | con distorsión | Desconocido |
| 1985 | Dougenik et al. | Método de distorsión de la lámina de goma [18] | área contigua | con distorsión | Sí, pero no garantizado |
| 1986 | Tobler | Método pseudo-cartograma | área contigua | con distorsión | Sí |
| 1987 | Snyder | Lupa de proyecciones de mapas azimutales. | distancia radial | Desconocido | Desconocido |
| 1989 | Cauvin et al. | Mapas de Piezopleth | área contigua | con distorsión | Desconocido |
| 1990 | Torguson | Método de cierre poligonal interactivo | área contigua | con distorsión | Desconocido |
| 1990 | Dorling | Método de la máquina de autómatas celulares | área contigua | con distorsión | Sí |
| 1993 | Gusein-Zade, Tikunov | Método de línea integral | área contigua | con distorsión | Sí |
| 1996 | Dorling | Cartograma circular | área no contigua | no (círculos) | No |
| 1997 | Sarkar, Brown | Vistas gráficas de ojo de pez | distancia radial | Desconocido | Desconocido |
| 1997 | Edelsbrunner , Waupotitsch | Enfoque basado en la combinación | área contigua | con distorsión | Desconocido |
| 1998 | Kocmoud, casa | Enfoque basado en restricciones | área contigua | con distorsión | Sí |
| 2001 | Keim , Norte, Panse | CartoDraw [23] | área contigua | con distorsión | Sí, con garantía algorítmica. |
| 2004 | Gastner, Newman | Método basado en la difusión [4] | área contigua | con distorsión | Sí, con garantía algorítmica. |
| 2004 | Sluga | Lastna tehnika za izdelavo anamorfoz | área contigua | con distorsión | Desconocido |
| 2004 | van Kreveld, Speckmann | Cartograma rectangular [24] | área contigua | no (rectángulos) | No |
| 2004 | Heilmann,Keim et al. | RecMap [19] | área no contigua | no (rectángulos) | No |
| 2005 | Keim , Norte, Panse | Cartogramas basados en el eje medial [25] | área contigua | con distorsión | Sí, con garantía algorítmica. |
| 2009 | Heriques, Bação, Lobo | Carto-SOM | área contigua | con distorsión | Sí |
| 2013 | Shipeng Sun | Opti-DCN [17] y Carto3F [15] | área contigua | con distorsión | Sí, con garantía algorítmica. |
| 2014 | BS Daya Sagar | Cartogramas basados en la morfología matemática | área contigua | Con distorsión local, pero sin distorsión global. | No |
| 2018 | Gastner, Seguy, Más | Método rápido basado en el flujo [26] | área contigua | con distorsión | Sí, con garantía algorítmica. |
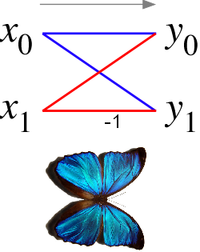











No hay comentarios:
Publicar un comentario