DIAGRAMAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

No debe confundirse con el diagrama de Hasse .

Diagrama de Hess con datos de SDSS b > 80 grados

Un diagrama de Hess representa la densidad relativa de la aparición de estrellas en diferentes posiciones de color-magnitud del diagrama de Hertzsprung-Russell para una galaxia dada o una población estelar resuelta. El diagrama lleva el nombre de R. Hess, quien lo originó en 1924. ^[1] Su uso se remonta a al menos 1948. ^[2]

Los diagramas de Hess se utilizan ampliamente en el estudio de sistemas estelares de resolución discreta en y alrededor de la Vía Láctea. Específicamente, en el análisis de cúmulos globulares , galaxias satélitey corrientes estelares .

Un diagrama de influencia ( ID ) (también llamado diagrama de relevancia , diagrama de decisión o red de decisión ) es una representación gráfica y matemática compacta de una situación de decisión. Es una generalización de una red bayesiana , en la que no solo se pueden modelar y resolver los problemas de inferencia probabilística , sino también los problemas de toma de decisiones (siguiendo el criterio de utilidad máxima esperada ).

ID fue desarrollado por primera vez a mediados de la década de 1970 por analistas de decisión con una semántica intuitiva que es fácil de entender. Ahora se adopta ampliamente y se convierte en una alternativa al árbol de decisión que generalmente sufre un crecimiento exponencial en el número de ramas con cada variable modelada. ID es directamente aplicable en el análisis de decisiones del equipo , ya que permite que el intercambio incompleto de información entre los miembros del equipo se pueda modelar y resolver explícitamente. Las extensiones de ID también encuentran su uso en la teoría de juegos como una representación alternativa del árbol de juegos .

Semántica [ editar ]

Una ID es un gráfico acíclico dirigido con tres tipos (más un subtipo) de nodo y tres tipos de arco (o flecha) entre nodos.

Nodos:

• El nodo de decisión (correspondiente a cada decisión que debe tomarse) se dibuja como un rectángulo.
• El nodo de incertidumbre (correspondiente a cada incertidumbre a modelar) se dibuja como un óvalo.

• El nodo determinista (que corresponde al tipo especial de incertidumbre de que su resultado se conoce determinísticamente siempre que también se conoce el resultado de algunas otras incertidumbres) se dibuja como un doble óvalo.

• El nodo de valor (correspondiente a cada componente de la función de utilidad Von Neumann-Morgenstern separable adicionalmente ) se dibuja como un octágono (o diamante).

Arcos:

• Los arcos funcionales (que terminan en el nodo de valor) indican que uno de los componentes de la función de utilidad separable aditivamente es una función de todos los nodos en sus colas.
• Los arcos condicionales (que terminan en el nodo de incertidumbre) indican que la incertidumbre en sus cabezas está condabilísticamente condicionada en todos los nodos en sus colas.

• Los arcos condicionales (que terminan en un nodo determinista) indican que la incertidumbre en sus cabezas está condicionada de forma determinista en todos los nodos en sus colas.

• Los arcos informativos (que terminan en el nodo de decisión) indican que la decisión en sus cabezas se toma con el resultado de todos los nodos en sus colas conocidas de antemano.

Dada una identificación adecuadamente estructurada:

• Los nodos de decisión y los arcos de información entrante establecen colectivamente las alternativas (qué se puede hacer cuando el resultado de ciertas decisiones y / o incertidumbres se conocen de antemano)
• Los nodos de incertidumbre / deterministas y los arcos condicionales entrantes modelan colectivamente la información (lo que se conoce y sus relaciones probabilísticas / deterministas)
• Los nodos de valor y los arcos funcionales entrantes cuantifican colectivamente la preferencia (cómo se prefieren las cosas entre sí).

Alternativa, información y preferencia se denominan base de decisión en el análisis de decisión, representan tres componentes requeridos de cualquier situación de decisión válida.

Formalmente, el diagrama semántico de influencia se basa en la construcción secuencial de nodos y arcos, lo que implica una especificación de todas las independencias condicionales en el diagrama. La especificación está definida por la$${\ displaystyle d}Criterio de separación de la red bayesiana. De acuerdo con esta semántica, cada nodo es probabilísticamente independiente en sus nodos no sucesores dado el resultado de sus nodos predecesores inmediatos. Igualmente, un arco faltante entre nodo sin valor.$${\ displaystyle X} y nodo sin valor $${\ displaystyle Y} Implica que existe un conjunto de nodos sin valor. $${\ displaystyle Z}, por ejemplo, los padres de $${\ displaystyle Y}, que rinde $${\ displaystyle Y} independiente de $${\ displaystyle X} Dado el resultado de los nodos en $${\ displaystyle Z}.

Ejemplo [ editar ]

Diagrama de influencia simple para tomar decisiones sobre la actividad de vacaciones.

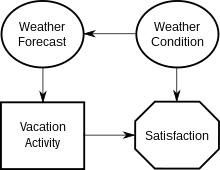
Considere el simple diagrama de influencia que representa una situación en la que un tomador de decisiones está planeando sus vacaciones.

• Hay 1 nodo de decisión ( Actividad de vacaciones ), 2 nodos de incertidumbre ( Condición del tiempo, Pronóstico del tiempo ) y 1 nodo de valor ( Satisfacción ).
• Hay 2 arcos funcionales (que terminan en Satisfacción ), 1 arco condicional (que termina en Pronóstico del tiempo ) y 1 arco informativo (que termina en Actividad de vacaciones ).

• Los arcos funcionales que terminan en Satisfacción indican que la Satisfacción es una función de utilidad de la Condición Meteorológica y la Actividad de Vacaciones . En otras palabras, su satisfacción puede cuantificarse si saben cómo es el clima y cuál es su elección de actividad. (Tenga en cuenta que no valoran el pronóstico del tiempo directamente)
• El arco condicional que termina en Pronóstico del tiempo indica que creen que el Pronóstico del tiempo y la Condición del tiempo pueden ser dependientes.
• El arco informativo que termina en la Actividad de Vacaciones indica que solo conocerán el Pronóstico del Tiempo , no la Condición del Tiempo , cuando hagan su elección. En otras palabras, el clima real se conocerá después de que hagan su elección, y solo el pronóstico es lo que pueden contar en esta etapa.

• También sigue semánticamente, por ejemplo, que la Actividad de vacaciones es independiente en (irrelevante para) Condición del clima dado que se conoce el Pronóstico del tiempo .

Aplicabilidad al valor de la información [ editar ]

El ejemplo anterior destaca el poder del diagrama de influencia al representar un concepto extremadamente importante en el análisis de decisiones conocido como el valor de la información . Considere los siguientes tres escenarios;

• Escenario 1: El tomador de decisiones podría tomar su decisión de Actividad de vacaciones al mismotiempo que sabe cómo será la condición climática . Esto corresponde a la adición de un arco informativo adicional de la Condición del clima a la Actividad de vacaciones en el diagrama de influencia anterior.
• Escenario 2: El diagrama de influencia original como se muestra arriba.
• Escenario 3: el tomador de decisiones toma su decisión sin siquiera saber el Pronóstico del Tiempo . Esto corresponde a eliminar el arco informativo del Pronóstico del tiempo a la Actividad de vacaciones en el diagrama de influencia anterior.

El escenario 1 es el mejor escenario posible para esta situación de decisión, ya que ya no hay incertidumbre sobre lo que les importa ( condición climática ) al tomar su decisión. Sin embargo, el escenario 3 es el peor escenario posible para esta situación de decisión, ya que deben tomar su decisión sin ninguna sugerencia ( Pronóstico del tiempo ) sobre lo que les interesa ( Condición del clima ).

El tomador de decisiones generalmente está mejor (definitivamente no peor, en promedio) para pasar del escenario 3 al escenario 2 a través de la adquisición de nueva información. Lo máximo que deberían estar dispuestos a pagar por tal movimiento se llama el valor de la información sobre el pronóstico del tiempo , que es esencialmente el valor de la información imperfecta sobre la condición del tiempo .

Del mismo modo, es lo mejor para quienes toman decisiones pasar del escenario 3 al escenario 1. Lo máximo que deberían estar dispuestos a pagar por dicho movimiento se denomina valor de información perfecta sobre la condición del clima .

La aplicabilidad de esta ID simple y el valor del concepto de información es tremendo, especialmente en la toma de decisiones médicas cuando la mayoría de las decisiones se deben tomar con información imperfecta sobre sus pacientes, enfermedades, etc.

Conceptos relacionados [ editar ]

Los diagramas de influencia son jerárquicos y pueden definirse en términos de su estructura o en mayor detalle en términos de la relación funcional y numérica entre los elementos del diagrama. Un ID que se define de manera consistente en todos los niveles (estructura, función y número) es una representación matemática bien definida y se conoce como un diagrama de influencia bien formado (WFID). Las WFID se pueden evaluar utilizando lasoperaciones de reversión y eliminación para obtener respuestas a una gran clase de preguntas probabilísticas, inferenciales y de decisión. Investigadores de inteligencia artificial han desarrollado técnicas más recientes relacionadas con la inferencia de la red bayesiana ( propagación de creencias ).

Un diagrama de influencia que solo tiene nodos de incertidumbre (es decir, una red bayesiana) también se denomina diagrama de relevancia . Un arco que conecta el nodo A a B implica no solo que " A es relevante para B ", sino también que " B es relevante para A " (es decir, relevancia es una relación simétrica ).

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Diagrama de Venn que muestra relaciones aditivas y sustractivas entre varias medidas de información asociadas con las variables correlacionadas X e Y. El área contenida por ambos círculos es la entropía conjunta H (X, Y). El círculo a la izquierda (rojo y violeta) es la entropía individual H (X), y el rojo es la entropía condicional H (X | Y). El círculo a la derecha (azul y violeta) es H (Y), con el azul siendo H (Y | X). El violeta es la información mutua I (X; Y).

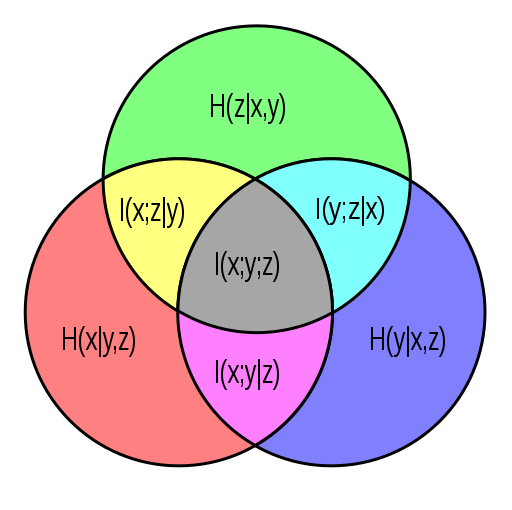
Un diagrama de información es un tipo de diagrama de Vennutilizado en la teoría de la información para ilustrar las relaciones entre las medidas básicas de información de Shannon : entropía , entropía conjunta , entropía condicional e información mutua . ^{[1] [2] Los} diagramas de información son una herramienta pedagógica útil para enseñar y aprender sobre estas medidas básicas de información, pero el uso de estos diagramas conlleva algunas implicaciones no triviales. Por ejemplo, la entropía de Shannon en el contexto de un diagrama de información debe tomarse como una medida firmada . (Ver el artículoTeoría de la información y teoría de la medida para más información.

El diagrama de Venn de las medidas teóricas de la información para tres variables x, y y z. Cada círculo representa una entropía individual : H (x) es el círculo inferior izquierdo, H (y) la derecha inferior, y H (z) es el círculo superior. Las intersecciones de cualquiera de los dos círculos representan la información mutua de las dos variables asociadas (por ejemplo, I (x; z) es amarillo y gris). La unión de cualquiera de los dos círculos es la entropía conjunta para las dos variables asociadas (por ejemplo, H (x, y) es todo menos verde). La entropía conjunta H (x, y, z) de las tres variables es la unión de los tres círculos. Se divide en 7 partes, rojo, azul y verde, siendo las entropías condicionales H (x | y, z), H (y | x, z), H (z | x, y) respectivamente, amarillo, magenta y cian siendo elinformación mutua condicional I (x; z | y), I (y; z | x) e I (x; y | z) respectivamente, y gris es la información mutua multivariable I (x; y; z). La información mutua multivariable es la única de todas que puede ser negativa.