Un cladograma (del griego clados "rama" y gramma "carácter") es un diagrama usado en la cladística para mostrar las relaciones entre los organismos. Sin embargo, un cladograma no es un árbol evolutivo porque no muestra cómo se relacionan los antepasados con los descendientes, ni muestra cuánto han cambiado; sin embargo, muchos árboles evolutivos pueden inferirse de un solo cladograma. [1] [2] [3] [4] [5] Un cladograma usa líneas que se ramifican en diferentes direcciones que terminan en un clado , un grupo de organismos con un último ancestro común. Hay muchas formas de cladogramas pero todas tienen líneas que se derivan de otras líneas. Las líneas se pueden remontar a donde se ramifican. Estos puntos de ramificación representan un ancestro hipotético (no una entidad real) que se puede inferir para mostrar los rasgos compartidos entre los taxones terminales que se encuentran por encima de él. [4] [6] Este ancestro hipotético podría entonces proporcionar pistas sobre el orden de evolución de varias características, adaptación y otras narraciones evolutivas sobre los ancestros. Aunque tradicionalmente tales cladogramas se generaron en gran medida sobre la base de caracteres morfológicos, datos de secuenciación de ADN y ARN y filogenética computacional ahora se utilizan con mucha frecuencia en la generación de cladogramas, ya sea solos o en combinación con la morfología.
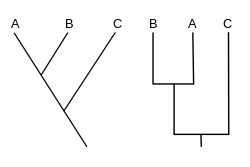
Molecular frente a los datos morfológicos [ editar ]
Las características utilizadas para crear un cladograma pueden clasificarse aproximadamente como morfológicas (cráneo sinápsido, sangre caliente, notocorda , unicelular, etc.) o molecular (ADN, ARN u otra información genética). [7] Antes del advenimiento de la secuenciación del ADN, el análisis cladístico utilizaba principalmente datos morfológicos. También se pueden utilizar datos de comportamiento (para animales). [8]
A medida que la secuenciación del ADN se ha vuelto más barata y más fácil, la sistemática molecular se ha convertido en una forma cada vez más popular de inferir hipótesis filogenéticas. [9] El uso de un criterio de parsimonia es solo uno de los varios métodos para inferir una filogenia a partir de datos moleculares. Los enfoques como la máxima probabilidad , que incorporan modelos explícitos de evolución de secuencia, son formas no hennigianas de evaluar los datos de secuencia. Otro método poderoso para reconstruir las filogenias es el uso de marcadores de retrotransposón genómicos , que se cree que son menos propensos al problema de la reversión.Eso plaga los datos de secuencia. En general, también se supone que tienen una baja incidencia de homoplasias porque se pensaba que su integración en el genoma era completamente aleatoria; Sin embargo, esto parece al menos a veces no ser el caso.
Plesiomorfías y sinapomorfías [ editar ]
Los investigadores deben decidir qué estados de carácter son "ancestrales" ( plesiomorphies ) y cuáles se derivan ( synapomorphies ), porque solo los estados de carácter sinapomórficos proporcionan evidencia de agrupación. [10] Esta determinación generalmente se realiza en comparación con los estados de carácter de uno o más grupos externos . Los estados compartidos entre el grupo externo y algunos miembros del grupo interno son simplesiomorfías; Los estados que están presentes solo en un subconjunto del in-group son sinapomorfías. Tenga en cuenta que los estados de caracteres exclusivos de un solo terminal (autapomorfías) no proporcionan evidencia de agrupación. La elección de un grupo externo es un paso crucial en el análisis cladístico porque diferentes grupos externos pueden producir árboles con topologías profundamente diferentes.
Homoplasias [ editar ]
Una homoplasia es un estado de carácter que es compartido por dos o más taxones debido a alguna causa diferente a la ascendencia común. [11]Los dos tipos principales de homoplasia son la convergencia (evolución del "mismo" carácter en al menos dos linajes distintos) y la reversión (el retorno a un estado de carácter ancestral). Los personajes que obviamente son homoplásticos, como el pelaje blanco en diferentes linajes de mamíferos árticos, no deben incluirse como un personaje en un análisis filogenético, ya que no contribuyen en nada a nuestra comprensión de las relaciones. Sin embargo, la homoplasia a menudo no es evidente a partir de la inspección del propio personaje (como en la secuencia de ADN, por ejemplo), y luego se detecta por su incongruencia (distribución irreprochable) en un cladograma más parsimonioso. Tenga en cuenta que los caracteres que son homoplásticos todavía pueden contener señal filogenética. [12]
Un ejemplo bien conocido de homoplasia debido a la evolución convergente sería el carácter, "presencia de alas". Aunque las alas de las aves, los murciélagos y los insectos tienen la misma función, cada una evolucionó de manera independiente, como puede verse en su anatomía . Si se puntuara a un pájaro, murciélago y un insecto alado para el personaje, "presencia de alas", se introducirá una homoplasia en el conjunto de datos, y esto podría confundir el análisis, lo que posiblemente resulte en una falsa hipótesis de relaciones. Por supuesto, la única razón por la cual una homoplasia es reconocible en primer lugar es porque hay otros personajes que implican un patrón de relaciones que revelan su distribución homoplástica.
Lo que no es un cladograma [ editar ]
Esta sección no cita ninguna fuente . ( Febrero de 2017 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )
|
Un cladograma es el resultado esquemático de un análisis, que agrupa a los taxones basándose únicamente en las sinapomorfías. Hay muchos otros algoritmos filogenéticos que tratan los datos de manera algo diferente y dan como resultado árboles filogenéticos que parecen cladogramas pero no son cladogramas. Por ejemplo, los algoritmos fenéticos, como UPGMA y Neighbor-Joining, se agrupan por similitud general y tratan tanto las sinapomorfías como las simplesiomorfías como evidencia de agrupación. Los diagramas resultantes son fenogramos, no cladogramas. De manera similar, los resultados de métodos basados en modelos La probabilidad o los enfoques bayesianos que toman en cuenta tanto el orden de bifurcación como la "longitud de bifurcación", cuentan tanto las sinapomorfias como las autapomorfías como evidencia a favor o en contra de la agrupación. Los diagramas que resultan de este tipo de análisis tampoco son cladogramas.
La selección cladograma [ editar ]
Hay varios algoritmos disponibles para identificar el "mejor" cladograma. [14] La mayoría de los algoritmos usan una métrica para medir qué tan consistente es un cladograma candidato con los datos. La mayoría de los algoritmos de cladogramas utilizan las técnicas matemáticas de optimización y minimización.
En general, los algoritmos de generación de cladogramas deben implementarse como programas informáticos, aunque algunos algoritmos pueden realizarse manualmente cuando los conjuntos de datos son modestos (por ejemplo, solo algunas especies y algunas características).
Algunos algoritmos son útiles solo cuando los datos característicos son moleculares (ADN, ARN); otros algoritmos son útiles solo cuando los datos característicos son morfológicos. Se pueden usar otros algoritmos cuando los datos característicos incluyen datos moleculares y morfológicos.
Los algoritmos para cladogramas u otros tipos de árboles filogenéticos incluyen mínimos cuadrados , unión de vecinos , parsimonia , probabilidad máxima e inferencia bayesiana .
Los biólogos a veces usan el término parsimonia para un tipo específico de algoritmo de generación de cladogramas y, a veces, como un término general para todos los algoritmos filogenéticos. [15]
Los algoritmos que realizan tareas de optimización (como la creación de cladogramas) pueden ser sensibles al orden en que se presentan los datos de entrada (la lista de especies y sus características). Ingresar los datos en varios órdenes puede hacer que el mismo algoritmo produzca diferentes cladogramas "mejores". En estas situaciones, el usuario debe ingresar los datos en varios pedidos y comparar los resultados.
El uso de diferentes algoritmos en un solo conjunto de datos a veces puede producir diferentes cladogramas "mejores", porque cada algoritmo puede tener una definición única de lo que es "mejor".
Debido al número astronómico de posibles cladogramas, los algoritmos no pueden garantizar que la solución sea la mejor solución en general. Se seleccionará un cladograma no óptimo si el programa establece un mínimo local en lugar del mínimo global deseado. [16] Para ayudar a resolver este problema, muchos algoritmos de cladogramas utilizan un enfoque de recocido simulado para aumentar la probabilidad de que el cladograma seleccionado sea el óptimo. [17]
La posición basal es la dirección de la base (o raíz) de un árbol o cladograma filogenético enraizado. Un clado basal es el clado más antiguo (de un rango taxonómico dado [a]) para ramificarse dentro de un clado más grande.
Estadística [ editar ]
Prueba de diferencia de longitud de incongruencia (o prueba de homogeneidad de partición) [ editar ]
La prueba de diferencia de longitud de incongruencia (ILD) es una medida de cómo la combinación de diferentes conjuntos de datos (por ejemplo, genes morfológicos y moleculares, de plástidos y nucleares) contribuye a un árbol más largo. Se mide primero calculando la longitud total del árbol de cada partición y sumándolas. Luego, las réplicas se realizan haciendo particiones ensambladas aleatoriamente que consisten en las particiones originales. Las longitudes se suman. Se obtiene un valor de p de 0.01 para 100 repeticiones si 99 repeticiones tienen longitudes de árbol combinadas más largas.
La medición de homoplasia [ editar ]
Algunas medidas intentan medir la cantidad de homoplasia en un conjunto de datos con referencia a un árbol, [18]aunque no está necesariamente claro exactamente qué propiedad pretenden cuantificar estas medidas [19]
Indice de consistencia [ editar ]
El índice de consistencia (IC) mide la consistencia de un árbol para un conjunto de datos, una medida de la cantidad mínima de homoplasia implícita en el árbol. [20] Se calcula contando el número mínimo de cambios en un conjunto de datos y dividiéndolo por el número real de cambios necesarios para el cladograma. [20] También se puede calcular un índice de consistencia para un carácter individual i , denotado c i .
Además de reflejar la cantidad de homoplasia, la métrica también refleja el número de taxones en el conjunto de datos, [21] (en menor medida) el número de caracteres en un conjunto de datos, [22] el grado en que cada personaje lleva información filogenética, [ 23] y la forma en que se codifican los caracteres aditivos, lo que hace que no sean aptos para el propósito. [24]
c i ocupa un rango de 1 a 1 / [ n.taxa / 2] en caracteres binarios con una distribución de estado par; su valor mínimo es mayor cuando los estados no se distribuyen uniformemente. [23] [18] En general, para un carácter binario o no binario con, c i ocupa un rango de 1 a. [23]
Índice de retención [ editar ]
El índice de retención (RI) se propuso como una mejora del IC "para ciertas aplicaciones" [25] Esta métrica también pretende medir la cantidad de homoplasia, pero también mide qué tan bien las sinapomorfías explican el árbol. Se calcula tomando el (número máximo de cambios en un árbol menos el número de cambios en el árbol) y dividiéndolo por (número máximo de cambios en el árbol menos el número mínimo de cambios en el conjunto de datos).
El índice de consistencia reescalado (RC) se obtiene multiplicando el IC por el RI; en efecto, esto extiende el rango del IC, de modo que su valor mínimo alcanzable teóricamente se vuelve a escalar a 0, con su máximo restante en 1. [18] [25] El índice de homoplasia (HI) es simplemente 1 - CI.
Homoplasia coeficiente de exceso [ editar ]
Esto mide la cantidad de homoplasia observada en un árbol en relación con la cantidad máxima de homoplasia que podría estar presente teóricamente - 1 - (exceso de homoplasia observado) / (exceso de homoplasia máximo). [22] Un valor de 1 indica que no hay homoplasia; 0 representa tanta homoplasia como habría en un conjunto de datos completamente aleatorio, y los valores negativos indican aún más homoplasia (y tienden a ocurrir solo en ejemplos artificiales). [22] La HER se presenta como la mejor medida de homoplasia actualmente disponible.
Un diagrama de cluster o diagrama de clustering es un tipo general de diagrama , que representa algún tipo de cluster. Un grupo en general es un grupo o grupo de varios elementos discretos que están cerca uno del otro.
El diagrama de clúster de cifras de un clúster, tal como un diagrama de red de las figuras A a la red , un diagrama de flujo de un proceso o movimiento de objetos, y un diagrama de árbol un resumen árbol . Pero todos estos diagramas se pueden considerar interconectados: un diagrama de red se puede ver como un tipo de diagrama de grupo ordenado y ordenado. Un diagrama de clúster es un tipo de malla de diagrama de red. Un diagrama de flujo puede verse como un tipo de línea de diagrama de red, y un diagrama de árbol es un tipo de diagrama de red de árbol .
Tipos de diagramas de cluster [ editar ]
Tipos específicos de diagramas de cluster son:
- En arquitectura, un diagrama de comparación a veces se llama diagrama de clúster. [1]
- En los diagramas astronómicos de cúmulos de estrellas , cúmulos de galaxias o cúmulos globulares .
- En la lluvia de ideas de un diagrama de clúster también se llama diagrama de nube . Pueden considerarse "son un tipo de organizador gráfico no lineal que puede ayudar a sistematizar la generación de ideas basadas en un tema central. El uso de este tipo de diagrama ... puede hacer una lluvia de ideas de un tema, asociarse con una idea o Explorar un nuevo tema ". [2] Además, el término diagramas de conglomerados se usa a veces como sinónimo de mapas mentales ". [3]
- En ciencias de la computación, los diagramas más complejos de redes de computadoras , arquitectura de computadoras , sistemas de archivos e Internet pueden considerarse diagramas de clústeres.
- En la visualización de información, la representación visual específica de colecciones a gran escala de información no numérica a veces se dibuja en forma de diagrama de grupo.
- En la teoría cuántica de campos, por ejemplo, según Crawford (1998), el llamado diagrama de clúster acoplado es un "formalismo esquemático simple popularizado por Kucharski y Bartlett [en 1986] por el cual uno puede construir las ecuaciones de amplitud y energía del clúster acoplado mucho más rápido que por aplicación directa del teorema de Wick ". [4]
- En el Lenguaje de modelado unificado (UML), todos los diagramas de estructura pueden considerarse diagramas de clúster. Estos diagramas de estructura enfatizan qué cosas deben estar en el sistema que se está modelando. UML encuentra aquí el Diagrama de clases , diagrama de componentes , diagrama de la estructura compuesta , diagrama de despliegue , diagrama de objeto , y el diagrama de paquetes .











No hay comentarios:
Publicar un comentario