En matemáticas, y especialmente en la teoría de categorías , un diagrama conmutativo es un diagrama tal que todas las rutas dirigidas en el diagrama con los mismos puntos de inicio y finales conducen al mismo resultado. Los diagramas conmutativos desempeñan el papel en la teoría de categorías que las ecuaciones juegan en el álgebra(ver Barr-Wells, Sección 1.7).
Descripción [ editar ]
Partes del diagrama:
- objetos (también conocidos como vértices )
- Morfismos (también conocidos como flechas o aristas )
- camino o composición
Símbolos de flecha [ editar ]
- monomorfismos con una
- epimorfismos con una
- isomorfismos con una.
- la flecha discontinua representa típicamente la afirmación de que el morfismo indicado existe cuando se mantiene el resto del diagrama; la flecha puede ser etiquetada opcionalmente.
- Si la flecha punteada está etiquetada o , el morfismo es además único.
Estas convenciones son tan comunes que los textos a menudo no explican el significado de los diferentes tipos de flecha.
Verificando la conmutatividad [ editar ]
La conmutatividad tiene sentido para un polígono de cualquier número finito de lados (incluyendo solo 1 o 2), y un diagrama es conmutativo si cada subdiagrama poligonal es conmutativo.
Tenga en cuenta que un diagrama puede no ser conmutativo, es decir, la composición de diferentes rutas en el diagrama puede no dar el mismo resultado.
Frases [ editar ]
Se pueden usar frases como "este diagrama conmutativo" o "los conmutadores del diagrama".
Ejemplos [ editar ]
En el diagrama de abajo a la izquierda, que expresa el primer teorema de isomorfismo , la conmutatividad significa que mientras que en el diagrama de abajo a la derecha, la conmutatividad del cuadrado significa :
 |  |
Para que el diagrama a continuación conmute, debemos tener las tres igualdades: (1) (2) y (3) . Como la primera igualdad se sigue de las dos últimas, para que el diagrama se conmute basta con mostrar (2) y (3). Sin embargo, dado que la igualdad (3) generalmente no se sigue de las otras dos igualdades, para que este diagrama se conmute, generalmente no es suficiente para tener solo la igualdad (1) y (2).
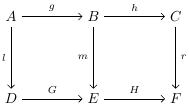 |
Diagrama persiguiendo [ editar ]
La búsqueda de diagramas (también llamada búsqueda diagramática ) es un método de prueba matemáticautilizado especialmente en álgebra homológica . Dado un diagrama conmutativo, una prueba por búsqueda de diagrama implica el uso formal de las propiedades del diagrama, como los mapas inyectivos o sobreyectivos , o las secuencias exactas . Se construye un silogismo para el cual la visualización gráfica del diagrama es solo una ayuda visual. Se sigue que uno termina "persiguiendo" elementos alrededor del diagrama, hasta que el elemento o resultado deseado se construye o verifica.
Los ejemplos de pruebas por búsqueda de diagramas incluyen las que se dan típicamente para el lema cinco , el lema serpiente , el lema zig-zag y el lema nueve .
En la teoría de la categoría superior [ editar ]
En la teoría de categorías superiores, uno considera no solo los objetos y las flechas, sino las flechas entre las flechas, las flechas entre las flechas entre las flechas, y así sucesivamente hasta el infinito . Por ejemplo, la categoría de categorías pequeñas Cat es naturalmente una categoría 2, con los funtores como flechas y las transformaciones naturales como las flechas entre los funtores. En esta configuración, los diagramas conmutativos también pueden incluir estas flechas superiores, que a menudo se representan en el siguiente estilo:. Por ejemplo, el siguiente diagrama (algo trivial) representa dos categorías C y D , junto con dos functors F , G : C → D y una transformación natural α : F ⇒ G :
Hay dos tipos de composición en una categoría 2 (llamada composición vertical y composición horizontal ), y también se pueden representar a través de diagramas de pegado , consulte la definición de 2 categorías # para ver ejemplos.
Diagramas como funtores [ editar ]
Un diagrama conmutativo en una categoría C puede interpretarse como un funtor de una categoría de índice J a C; uno llama al funtor un diagrama .
Más formalmente, un diagrama conmutativo es una visualización de un diagrama indexado por una categoría de poset :
- uno dibuja un nodo para cada objeto en la categoría de índice,
- una flecha para un conjunto generador de morfismos,
- omitiendo los mapas de identidad y los morfismos que pueden expresarse como composiciones,
- y la conmutatividad del diagrama (la igualdad de diferentes composiciones de mapas entre dos objetos) corresponde a la singularidad de un mapa entre dos objetos en una categoría de poset.
A la inversa, dado un diagrama conmutativo, define una categoría poset:
- los objetos son los nodos,
- hay un morfismo entre cualquiera de los dos objetos si y solo si hay una ruta (dirigida) entre los nodos,
- con la relación de que este morfismo es único (cualquier composición de mapas se define por su dominio y objetivo: este es el axioma de conmutatividad).
Sin embargo, no todos los diagramas de conmutación (la noción de diagrama generaliza estrictamente el diagrama conmutativo): más simple, el diagrama de un solo objeto con un endomorfismo (), o con dos flechas paralelas (, es decir, , a veces llamado el carcaj libre ), tal como se utiliza en la definición de ecualizador no necesita conmutar. Además, los diagramas pueden ser complicados o imposibles de dibujar cuando el número de objetos o morfismos es grande (o incluso infinito).
El diagrama de comparación o diagrama comparativo es un tipo general de diagrama , en el que se realiza una comparación entre dos o más objetos, fenómenos o grupos de datos. [1] Un diagrama de comparación o puede ofrecer información cualitativa y / o cuantitativa. Este tipo de diagrama también se puede llamar tabla de comparación o tabla de comparación. El diagrama en sí se refiere a veces como un diagrama de grupo .
Descripción general [ editar ]
Un diagrama de comparación es un tipo general de diagrama, es decir, una clase de diagramas y gráficos específicos, en el que se realiza una comparación entre dos o más objetos, fenómenos o grupos de datos. Son una herramienta para la comparación visual .
Cuando se trata de comparar datos, se pueden determinar cinco tipos básicos de comparación. [2]
- Comparación de componentes, por ejemplo las piezas del gráfico circular.
- Comparación de elementos, por ejemplo las barras en un gráfico de barras
- Comparación de series de tiempo, por ejemplo, las barras en un histograma o la curva de un gráfico de líneas
- Comparación de la distribución de frecuencias, por ejemplo, la distribución en un histograma o gráfico de líneas
- Comparación de correlación, por ejemplo, en un diagrama de puntos específico
Los diagramas de comparación se pueden utilizar en proyectos de investigación , para dar una visión general de las posibilidades existentes y para validar modelos. [3] Se puede utilizar en la toma de decisiones al presentar alternativas para una mayor selección. Y se puede utilizar en la educación para mostrar la variedad en una población específica.
Historia [ editar ]
Orígenes [ editar ]
Los cuadros de comparación se originan desde finales del siglo XVIII y principios del XIX. Una de sus raíces es la carta náutica del siglo XVIII , que podría ofrecer una comparación de los perfiles costeros o costeros. Estos fueron popularizados por el cartógrafo inglés y un editor de mapas William Faden (1749–1836). [4]
Otra raíz de los diagramas de comparación son los primeros mapas temáticos . A finales del siglo XVIII, August Friedrich Wilhelm Cromepublicó uno de los primeros mapas temáticos económicos. [5] [6] Su "Groessen Karte von Europa" de 1785 comparó los tamaños de todos los países europeos existentes en ese momento. Este trabajo inspiró a científicos posteriores, como Alexander von Humboldt en Alemania, [7] [8]y Charles Dupin en Francia. [9] En sus obras. En Francia, en 1872, Charles Louis de Fourcroy presentó un diagrama similar, al que llamó "Table Poléométrique" (Tabla Poleométrica). [10]
A principios del siglo XIX, Alexander von Humboldt fue uno de los primeros en imaginar varias secciones transversales de montañas, incluido, por ejemplo, el "límite de nieves perpetuas en diferentes latitudes" o los diferentes tipos de vegetación en diferentes alturas. [11]Gran parte de este trabajo se publicó en 1914 "Atlas géographique et physique des régions équinoxiales du nouveau continente". [12] En 1805, Von Humboldt publicó un mapa (ver imagen), titulado "Ideen zu einer Geographie der Pflanzen nebst einem Naturgemälde der Tropenländer" (Ideas para una geografía de plantas, junto con una pintura de la naturaleza de los trópicos) en la que hizo una comparación de los diferentes tipos de planes en los trópicos y las alturas en las que crecieron.
Primeros cuadros comparativos [ editar ]
En la década de 1810 surgieron las primeras tablas de montañas comparativas formales. Los primeros ejemplos son:
- Vista comparativa de Charles Smith de las alturas de las montañas principales & c. In The World, publicado en Londres en 1816 [4]
- John Thomson 's una visión comparativa de las alturas de las montañas principales y otras elevaciones en el mundo. publicado en la edición de 1817 de Thomson New General Atlas. [13]
Otro tema popular se convirtió en el punto de vista comparativo de las longitudes de los ríos principales en un país o de todo el mundo. En 1822, William Home Lizars presentó un mapa titulado "Vista comparativa de las longitudes de los principales ríos de Escocia". [14] Y en 1826, Anthony Finley (1790–1840) publicó un "Mapa Comparativo de los Principios de los Ríos del Mundo".
Pronto aparecerían otros tipos de cuadros de comparación. Por ejemplo, el "Atlas completo: geográfico, histórico y comercial", publicado por William D. Ticknor en 1835 contenía una serie de diferentes diagramas de comparación y tablas en: [15]
- Tamaño de los continentes, océanos, islas.
- Alturas de las montañas
- Longitudes de ríos
- Tamaño del animal
- Tamaño de los planetas
- Alturas de monumentos
- Altura de los edificios
- Diferentes paises
Otros temas populares en los diagramas de comparación del siglo XIX fueron el tamaño de los lagos, la longitud de las cascadas y el tamaño de las islas.
Uno de los primeros mapas en comparar las longitudes de los ríos fue el "Mapa de los ríos principales en todo el mundo. Longitudes comparativas de los ríos principales en todo el mundo". por el economista político Henry Charles Carey e Isaac Lea publicaron su 1822 "Un completo atlas histórico, cronológico y geográfico de Estados Unidos". [16] En este mapa, las longitudes de los ríos se presentaron en un gráfico de barras con barras horizontales. En 1826, los mismos datos se presentaron en un gráfico de barras con barras verticales, titulado "Tabla de las longitudes comparativas de los principales ríos de todo el mundo" (ver imagen).
Siglo XX [ editar ]
En sus métodos gráficos para presentar hechos. Willard C. Brinton fue uno de los primeros en teorizar sobre la existencia y el papel o la comparación en gráficos estadísticos . Él estipuló que "el método gráfico se presta admirablemente para usarse al hacer comparaciones. Es sorprendente lo mucho más claro que aparecerán comparaciones simples de solo dos o tres elementos cuando su valor numérico se ponga en forma gráfica en lugar de en cifras". [17] Brinton mostró más de una docena de tipos diferentes de diagramas, lo que podría hacer una comparación simple, y dedicó otro capítulo a las comparaciones a lo largo del tiempo.
Tipos de diagramas de comparación [ editar ]
Existen diferentes tipos de diagramas de comparación llamados diagramas / tablas de comparación en teoría y práctica, tales como
- Tabla , datos visualizados en forma tabular.
- Modelos basados en matrices, por ejemplo el cuadro de mando integral.
- Gráficos cuantitativos tales como gráfico de líneas , gráfico de barras , gráfico circular , gráfico de radar , gráfico de burbujas , dispersión diagrama etc.
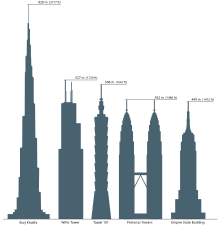
- Diagrama de comparación de escalas
- Mapa de comparación o mapa comparativo.





















No hay comentarios:
Publicar un comentario