sistema de ecuaciones lineales o no lineales es consistente si hay al menos un conjunto de valores para las incógnitas que satisfacen cada ecuación en el sistema, es decir, que cuando se sustituye en cada una de las ecuaciones hace que cada una La ecuación se mantiene verdadera como una identidad . En contraste, un sistema de ecuaciones es inconsistente si no hay un conjunto de valores para las incógnitas que satisfagan todas las ecuaciones.
Si un sistema de ecuaciones es inconsistente, entonces es posible manipular y combinar las ecuaciones para obtener información contradictoria, como 2 = 1, o x 3 + y 3 = 5 y x 3 + y 3 = 6 (lo que implica 5 = 6).
Ambos tipos de sistemas de ecuaciones, consistentes e inconsistentes, pueden estar sobredeterminados (con más ecuaciones que incógnitas), indeterminados (con menos ecuaciones que incógnitas) o determinados con exactitud.
Ejemplos simples [ editar ]
Indeterminado y consistente [ editar ]
El sistema
tiene un número infinito de soluciones, todas ellas con z = 1 (como puede verse al restar la primera ecuación de la segunda) y, por lo tanto, el sistema no lineal
Tiene infinitas soluciones, todas involucradas.
Indeterminado e inconsistente [ editar ]
El sistema
no tiene soluciones, como puede verse al restar la primera ecuación de la segunda para obtener el imposible 0 = 1.
El sistema no lineal.
no tiene soluciones, porque si una ecuación se resta de la otra obtenemos el imposible 0 = 3.
Exactamente determinado y consistente [ editar ]
El sistema
tiene exactamente una solución: x = 1, y = 2.
El sistema no lineal.
tiene las dos soluciones ( x, y ) = (1, 0) y ( x, y ) = (0, 1), mientras que
tiene un número infinito de soluciones porque la tercera ecuación es la primera ecuación más dos veces la segunda y, por lo tanto, no contiene información independiente; por lo tanto, cualquier valor de z se puede elegir y se puede encontrar que los valores de x e y satisfacen las dos primeras ecuaciones (y, por lo tanto, las terceras).
Exactamente determinado e inconsistente [ editar ]
El sistema
no tiene soluciones; la inconsistencia se puede ver al multiplicar la primera ecuación por 4 y al restar la segunda ecuación para obtener el imposible 0 = 2.
Igualmente,
es un sistema inconsistente porque la primera ecuación más dos veces la segunda menos la tercera contiene la contradicción 0 = 2.
Sobredeterminado y consistente [ editar ]
El sistema
tiene una solución, x = –1, y = 4, porque las dos primeras ecuaciones no se contradicen entre sí y la tercera ecuación es redundante (ya que contiene la misma información que se puede obtener de las dos primeras ecuaciones al multiplicar cada una por 2 y sumándolos).
El sistema
tiene una infinidad de soluciones ya que las tres ecuaciones dan la misma información entre sí (como se puede ver al multiplicar la primera ecuación por 3 o 7). Cualquier valor de y es parte de una solución, con el valor correspondiente de x siendo 7–2y.
El sistema no lineal.
tiene las tres soluciones ( x, y ) = (1, –1), (–1, 1) y (1, 1).
Sobredeterminado e inconsistente [ editar ]
El sistema
es inconsistente porque la última ecuación contradice la información incrustada en los dos primeros, como se ve al multiplicar cada uno de los dos primeros por 2 y sumarlos.
El sistema
es inconsistente porque la suma de las dos primeras ecuaciones contradice la tercera.
Criterios de consistencia [ editar ]
Como se puede ver en los ejemplos anteriores, la consistencia frente a la inconsistencia es un problema diferente al comparar los números de ecuaciones y las incógnitas.
Sistemas lineales [ editar ]
Un sistema lineal es consistente si y solo si su matriz de coeficientes tiene el mismo rango que su matriz aumentada (la matriz de coeficientes con una columna adicional agregada, siendo esa columna el vector de columnas de las constantes).
en el que a es distinto de cero.
El ajuste f ( x ) = 0 produce una ecuación cúbica de la forma
Las soluciones de esta ecuación se llaman raíces del polinomio f ( x ) . Si todos los coeficientes a , b , c y d de la ecuación cúbica son números reales , entonces tiene al menos una raíz real (esto es cierto para todos los polinomios de grado impar ). Todas las raíces de la ecuación cúbica se pueden encontrar algebraicamente . (Esto también se aplica a lasecuaciones cuadráticas (segundo grado) o quárticas (cuarto grado), pero no a las ecuaciones de grado superior, según el teorema de Abel-Ruffini.) Las raíces también se pueden encontrar trigonométricamente . Alternativamente, las aproximaciones numéricas de las raíces se pueden encontrar usando algoritmos de búsqueda de raíces como el método de Newton .
Los coeficientes no necesitan ser números complejos. Gran parte de lo que se cubre a continuación es válido para los coeficientes de cualquier campo con característica 0 o mayor que 3 . Las soluciones de la ecuación cúbica no pertenecen necesariamente al mismo campo que los coeficientes. Por ejemplo, algunas ecuaciones cúbicas con coeficientes racionales tienen raíces que son números complejos no racionales (e incluso no reales) .
Historia [ editar ]
Las ecuaciones cúbicas eran conocidas por los antiguos babilonios, griegos, chinos, indios y egipcios. [1] [2] [3] Se han encontrado tabletas cuneiformes babilónicas (del siglo XX al XVI aC) con tablas para calcular los cubos y las raíces cúbicas. [4] [5] Los babilonios podrían haber usado las tablas para resolver ecuaciones cúbicas, pero no existe evidencia para confirmar que lo hicieron. [6] El problema de duplicar el cubo involucra la ecuación cúbica estudiada más simple y antigua, y una para la cual los antiguos egipcios no creían que existiera una solución. [7]En el siglo V aC, Hipócrates.redujo este problema al de encontrar dos medias proporcionales entre una línea y otra de dos veces su longitud, pero no pudo resolverlo con una construcción de compás y regla , [8] una tarea que ahora se sabe que es imposible. Los métodos para resolver ecuaciones cúbicas aparecen en Los Nueve Capítulos sobre el Arte Matemático , un texto matemático chino compilado alrededor del siglo II aC y comentado por Liu Hui en el siglo III. [2] En el siglo III dC, el matemático griego Diophantus encontró soluciones enteras o racionales para algunas ecuaciones cúbicas bivariadas ( ecuaciones diofánticas ). [3] [9] Se cree que Hipócrates , Menaechmus y Arquímedes se han acercado a resolver el problema de duplicar el cubo utilizando secciones cónicas que se intersectan , [8] aunque los historiadores como Reviel Netz discuten si los griegos estaban pensando en ecuaciones cúbicas o solo en problemas que pueden conducir a una ecuaciones Algunos otros, como TL Heath , que tradujeron todas las obras de Arquímedes , no están de acuerdo, y aportan pruebas de que Arquímedes realmente resolvió ecuaciones cúbicas utilizando intersecciones de dos cónicas , pero también discutieron las condiciones donde las raíces son 0, 1 o 2. [10]
En el siglo séptimo, la dinastía Tang astrónomo matemático Wang Xiaotongen su tratado matemático titulado Jigu suanjing estableció sistemática y resolverse numéricamente 25 ecuaciones cúbicas de la forma x 3 + px 2 + qx = N , 23 de ellos con p , q ≠ 0 , y dos de ellos con q = 0 . [11]
En el siglo XI, el poeta-matemático persa, Omar Khayyam (1048–1131), hizo un progreso significativo en la teoría de las ecuaciones cúbicas. En un artículo anterior, descubrió que una ecuación cúbica puede tener más de una solución y afirmó que no se puede resolver con las construcciones de brújula y regla. También encontró una solución geométrica . [12] [13] En su último trabajo, el Tratado sobre Demostración de Problemas de Álgebra , escribió una clasificación completa de ecuaciones cúbicas con soluciones geométricas generales encontradas mediante la intersección de secciones cónicas . [14] [15]
En el siglo XII, el matemático indio Bhaskara II intentó la solución de ecuaciones cúbicas sin éxito general. Sin embargo, dio un ejemplo de una ecuación cúbica: x 3 + 12 x = 6 x 2 + 35 . [16] En el siglo XII, otro matemático persa , Sharaf al-Dīn al-Tūsī (1135–1213), escribió el Al-Muʿādalāt ( Tratado de ecuaciones ), que trataba ocho tipos de ecuaciones cúbicas con soluciones positivas y cinco tipos. de ecuaciones cúbicas que pueden no tener soluciones positivas. Usó lo que luego se conocería como el " método Ruffini - Horner " paraaproxima numéricamente la raíz de una ecuación cúbica. También utilizó los conceptos de máximos y mínimos de curvas para resolver ecuaciones cúbicas que pueden no tener soluciones positivas. [17] Comprendió la importancia del discriminante de la ecuación cúbica para encontrar soluciones algebraicas a ciertos tipos de ecuaciones cúbicas. [18]
En su libro Flos , Leonardo de Pisa, también conocido como Fibonacci (1170–1250), pudo aproximarse mucho a la solución positiva de la ecuación cúbica x 3 + 2 x 2 + 10 x = 20 . Escribiendo en números babilónicos , dio el resultado como 1,22,7,42,33,4,40 (equivalente a 1 + 22/60 + 7/60 2 + 42/60 3 + 33/60 4 + 4/60 5 + 40/60 6 ), que tiene un error relativo de aproximadamente 10 −9 . [19]
A principios del siglo XVI, el matemático italiano Scipione del Ferro (1465–1526) encontró un método para resolver una clase de ecuaciones cúbicas, a saber, las de la forma x 3 + mx = n . De hecho, todas las ecuaciones cúbicas pueden reducirse a esta forma si permitimos que m y n sean negativos, pero los números negativos no se conocían en ese momento. Del Ferro mantuvo en secreto su logro hasta poco antes de su muerte, cuando se lo contó a su alumno Antonio Fiore .
En 1530, Niccolò Tartaglia (1500–1557) recibió dos problemas en ecuaciones cúbicas de Zuanne da Coi y anunció que podía resolverlos. Pronto fue desafiado por Fiore, lo que llevó a una famosa competencia entre los dos. Cada participante tenía que aportar una cierta cantidad de dinero y proponer una serie de problemas para que su rival los resolviera. Quien resolviera más problemas en 30 días obtendría todo el dinero. Tartaglia recibió preguntas en la forma x 3 + mx = n , para las cuales había desarrollado un método general. Fiore recibió preguntas en la forma x 3 + mx 2 = n, lo que demostró ser demasiado difícil de resolver para él, y Tartaglia ganó el concurso.
Más tarde, Tartaglia fue persuadido por Gerolamo Cardano (1501–1576) para revelar su secreto para resolver ecuaciones cúbicas. En 1539, Tartaglia lo hizo solo con la condición de que Cardano nunca lo revelara y que si escribía un libro sobre cúbicos, le daría tiempo a Tartaglia para que publicara. Algunos años más tarde, Cardano se enteró del trabajo anterior de Ferro y publicó el método de Ferro en su libro Ars Magna.en 1545, lo que significa que Cardano le dio a Tartaglia seis años para publicar sus resultados (con el crédito otorgado a Tartaglia por una solución independiente). La promesa de Cardano con Tartaglia declaró que no publicaba el trabajo de Tartaglia, y Cardano sintió que estaba publicando Del Ferro's, para poder cumplir con la promesa. Sin embargo, esto llevó a un desafío a Cardano por parte de Tartaglia, que Cardano negó. El desafío fue finalmente aceptado por el estudiante de Cardano, Lodovico Ferrari(1522-1565). Ferrari lo hizo mejor que Tartaglia en la competencia, y Tartaglia perdió tanto su prestigio como sus ingresos. [20]
Cardano notó que el método de Tartaglia a veces requería que extrajera la raíz cuadrada de un número negativo. Incluso incluyó un cálculo con estos números complejos en Ars Magna , pero realmente no lo entendió. Rafael Bombelli estudió este tema en detalle [21] y, por lo tanto, a menudo se lo considera como el descubridor de números complejos.
François Viète (1540–1603) derivó de forma independiente la solución trigonométrica para la cúbica con tres raíces reales, y René Descartes (1596–1650) extendió el trabajo de Viète. [22]
Puntos críticos y punto de inflexión de una función cúbica [ editar ]
Los puntos críticos de una función son aquellos valores de xdonde la pendiente de la función es cero. Los puntos críticos de una función cúbica f definidos por f ( x ) = ax 3 + bx 2 + cx + d , se producen en los valores de x de modo que la derivada de la función cúbica es cero:
Las soluciones de esa ecuación son los puntos críticos de la ecuación cúbica y se dan, usando la fórmula cuadrática , por
La expresión dentro de la raíz cuadrada,
Determina qué tipo de puntos críticos tiene la función. Si Δ 0 > 0, entonces la función cúbica tiene un máximo local y un mínimo local. Si Δ 0 = 0 , entonces el punto de inflexión del cubic es el único punto crítico. Si Δ 0 <0 font=""> , entonces no hay puntos críticos. En los casos donde Δ 0 ≤ 0 , la función cúbica es estrictamente monotónica . El diagrama adyacente es un ejemplo del caso donde Δ 0 > 0 . Los otros dos casos no tienen el máximo local o el mínimo local, pero aún tienen un punto de inflexión.
El valor de Δ 0 también juega un papel importante en la determinación de la naturaleza de las raíces de la ecuación cúbica y en el cálculo de esas raíces; ver más abajo .
El punto de inflexión de una función es donde esa función cambia la concavidad . El punto de inflexión de nuestra función cúbica ocurre en:
un valor que también es importante para resolver la ecuación cúbica. La función cúbica tiene simetría de punto sobre su punto de inflexión .
Todo lo anterior asume que los coeficientes son reales, así como la variable x .
Solución general a la ecuación cúbica con coeficientes reales [ editar ]
Esta sección trata sobre cómo resolver la ecuación cúbica usando varios métodos. Para más detalles y pruebas ver más abajo . La ecuación cúbica general tiene la forma:
- ( 1 )
con un ≠ 0 .
Solución algebraica [ editar ]
La solución algebraica de la ecuación cúbica se puede derivar de varias maneras diferentes. (Véase por ejemplo el método de Cardano y el método de Vieta a continuación).
El discriminante [ editar ]
Los números de raíces reales y complejas están determinados por el discriminante de la ecuación cúbica,
Resulta que:
- Si Δ> 0 , entonces la ecuación tiene tres raíces reales distintas.
- Si Δ = 0 , entonces la ecuación tiene una raíz múltiple y todas sus raíces son reales.
- Si Δ <0 span=""> , entonces la ecuación tiene una raíz real y dos raíces conjugadas complejas no reales .
Fórmula Cardano [ editar ]
La solución de la ecuación cúbica general puede deducirse de la de la depresión cúbica
La fórmula de Cardano es la siguiente expresión de las soluciones de esta ecuación.
dónde denota la raíz cúbica real de X , si X es real (es decir,), o, en el otro caso, el valor principal de la función de raíz cúbica, que es la raíz cúbica con la parte real máxima .
Las otras dos soluciones se obtienen multiplicando una de las raíces cúbicas por y el otro por
Si p y q no son ambas reales, las mismas fórmulas siguen siendo correctas si, en la fórmula para la primera raíz, uno elige las raíces cúbicas para que su producto sea –p / 3 . (Si p y q son reales, las opciones anteriores para las raíces cúbicas satisfacen esta propiedad).
En el caso especial estas fórmulas siguen siendo correctas, pero hay una fórmula más simple disponible, donde una solución es 3qp , y las otras dos son iguales –3q2p .
Fórmula general [ editar ]
La solución general de la ecuación cúbica implica el primer cálculo:
(Si el discriminante Δ ya ha sido calculado, entonces la igualdad Δ 1 2 - 4Δ 0 3 = -27 a 2 Δ se puede utilizar para simplificar el cálculo de C ). Hay tres posibles raíces cúbicas que implica la expresión, de los cuales Al menos dos son números complejos no reales; cualquiera de éstos se puede elegir la hora de definir C . (Además, se puede elegir cualquier signo delante de la raíz cuadrada a menos que Δ 0 = 0, en cuyo caso el signo debe elegirse de modo que los dos términos dentro de la raíz cúbica no se cancelen).
La fórmula general para una de las raíces, en términos de los coeficientes, es la siguiente:
Tenga en cuenta que, si bien esta igualdad es válida para todas las C que no son cero , no es la forma más conveniente para múltiples raíces ( Δ = 0 ), que se trata en la siguiente sección. (El caso cuando C = 0 solo ocurre cuando Δ y Δ 0 son iguales a 0 y también se trata en la siguiente sección).
Las otras dos raíces de la ecuación cúbica se pueden determinar usando la misma igualdad, usando las otras dos opciones para la raíz cúbica en la ecuación para C : denota la primera opción simplemente como C , los otros se pueden escribir como (- 12 + 12 √ 3 i ) C y (- 12 - 12 √ 3 i ) C .
La igualdad anterior se puede expresar de manera compacta incluyendo las 3 raíces de la siguiente manera:
donde ξ = - 12 + 12 √ 3 i (que es una raíz cúbica de la unidad). En el caso de tres raíces reales, esta solución las expresa en términos de términos complejos no reales (ya que cualquier elección de C no es real) cuyos componentes imaginarios se compensan entre sí pero no pueden eliminarse de la fórmula .
Esta fórmula para las tres raíces se aplica incluso cuando los coeficientes en el cúbico no son reales, aunque el análisis del signo de Δ no se cumple, ya que Δ no es real en general.
Múltiples raíces, Δ = 0 [ editar ]
Si tanto Δ como Δ 0 son iguales a 0 , entonces la ecuación tiene una sola raíz (que es una raíz triple ):
y una raíz simple,
Soluciones trigonométricas e hiperbólicas [ editar ]
Reducción a un deprimido cúbico [ editar ]
Dividiendo ax 3 + bx 2 + cx + d = 0 por a y sustituyendo t - b3 a por x obtenemos la ecuación
- ( 2 )
dónde
El lado izquierdo de la ecuación ( 2 ) es un trinomio monico llamado cúbico deprimido , porque el término cuadrático tiene el coeficiente 0.
Cualquier fórmula para las raíces de un cúbico deprimido puede transformarse en una fórmula para las raíces de la ecuación ( 1 ) sustituyendo los valores anteriores por p y q y utilizando la relación x = t - b3 a .
Solución trigonométrica para tres raíces reales [ editar ]
Cuando una ecuación cúbica tiene tres raíces reales, las fórmulas que expresan estas raíces en términos de radicales involucran números complejos. Se ha demostrado que cuando ninguna de las tres raíces reales es racional, el casus irreducibilis , no se pueden expresar las raíces en términos de radicales reales. Sin embargo, se pueden obtener expresiones puramente reales de las soluciones utilizando funciones hipergeométricas , [23] o más elementalmente en términos de funciones trigonométricas , específicamente en términos de las funciones coseno y arccosina .
Las fórmulas que siguen, debido a François Viète , [22] son verdaderas en general (excepto cuando p = 0), y son puramente reales cuando la ecuación tiene tres raíces reales, pero involucran complejos cosenos y arccosinas cuando solo hay una raíz real .
Partiendo de la ecuación ( 2 ) , t 3 + pt + q = 0 , configuremos t = u cos θ . La idea es elegir u para hacer que la ecuación ( 2 ) coincida con la identidad
Combinando con la identidad anterior, obtenemos
y así las raíces son [24]
Esta fórmula implica solo términos reales si p <0 font=""> y el argumento de la arccosina está entre −1 y 1 . La última condición es equivalente a 4 p 3 + 27 q 2 ≤ 0 , lo que a su vez implica p <0 font=""> . Por lo tanto, la fórmula anterior para las raíces implica solo términos reales si y solo si las tres raíces son reales.
Denotando por C ( p , q ) el valor anterior de t 0 , y utilizando las desigualdades 0 ≤ arccos ( u ) ≤ π para un número real u tal que −1 ≤ u ≤ 1 , las tres raíces también pueden expresarse como
Si las tres raíces son reales, tenemos t 0 ≥ t 1 ≥ t 2 . Todas estas fórmulas pueden transformarse directamente en fórmulas para las raíces de la ecuación cúbica general ( 1 ) , utilizando la sustitución inversa descrita anteriormente .
Solución hiperbólica para una raíz real [ editar ]
Cuando solo hay una raíz real (y p 0 ), puede representarse de manera similar utilizando funciones hiperbólicas , como [25] [26]
Si p ≠ 0 y las desigualdades de la derecha no se satisfacen (el caso de tres raíces reales), las fórmulas siguen siendo válidas pero involucran cantidades complejas.
Cuando p = ± 3 , los valores anteriores de t 0 a veces se llaman la raíz cúbica de Chebyshev. [27] Más precisamente, los valores que implican cosenos y cosenos hiperbólicos definen, cuando p = −3 , la misma función analítica denotada C 1/3 ( q ) , que es la raíz cúbica de Chebyshev adecuada. El valor que involucra senos hiperbólicos se denota de manera similar S 1/3 ( q ) , cuando p = 3 .
Factorización [ editar ]
Si una función cúbica ax 3 + bx 2 + cx + d con coeficientes enteros es reducible sobre los números racionales, lo que significa que puede tenerse en cuenta en polinomios de menor grado con racionales coeficientes, entonces tiene una raíz racional, que se puede encontrar utilizando la prueba de raíz racional : Si la raíz r = m / n está totalmente reducida, después m es un factor de d y n es un factor de una , por lo que todas las combinaciones posibles de valores para m y n (tanto positivo como negativo para uno de ellos) se puede verificar si son raíces del cúbico.
La prueba de raíz racional también se puede usar para una ecuación cúbica con coeficientes racionales: mediante la multiplicación del mínimo común denominador de los coeficientes, se obtiene una ecuación con coeficientes enteros que tiene exactamente las mismas raíces.
La prueba de raíz racional es particularmente útil cuando hay tres raíces reales porque la solución algebraica expresa inútilmente las raíces reales en términos de entidades complejas ; Si la prueba produce una raíz racional, puede ser eliminada y las raíces restantes se pueden encontrar resolviendo una cuadrática. La prueba de raíz racional también es útil en presencia de una raíz real y dos complejas porque, de nuevo, si produce una raíz racional, permite que todas las raíces se escriban sin el uso de raíces cúbicas: si r es cualquier raíz de la raíz cúbicos, entonces podemos factorizar x - r usando la división larga polinomial para obtener
Por lo tanto, si conocemos una raíz, tal vez de la prueba racional de raíces, podemos encontrar las otras dos usando la fórmula cuadrática para encontrar las raíces del hacha cuadrática 2 + ( b + ar ) x + c + br + ar 2 , dando
Para las otras dos raíces.
Soluciones geométricas [ editar ]
La solución de Omar Khayyám [ editar ]
Como se muestra en este gráfico, para resolver la ecuación de tercer grado x 3 + m 2 x = n donde n > 0 , Omar Khayyám construyó la parábola y = x 2 / m , el círculo que tiene como diámetro el segmento de línea [0 , n / m 2 ] en el eje x positivo , y una línea vertical a través del punto sobre el x-Eje donde se intersectan el círculo y la parábola. La solución viene dada por la longitud del segmento de línea horizontal desde el origen hasta la intersección de la línea vertical y el eje x .
Una prueba moderna y simple del método es la siguiente: multiplicar la ecuación por x y reagrupar los términos da
El lado izquierdo es el valor de y 2 en la parábola. La ecuación del círculo es y 2 + x ( x - nm 2 ) = 0 , el lado derecho es el valor de y 2 en el círculo.
Solución con ángulo de trisector [ editar ]
Una ecuación cúbica con coeficientes reales se puede resolver geométricamente usando una brújula, una regla y un trisector de ángulo si y solo si tiene tres raíces reales. [28] : Thm. 1
Naturaleza de las raíces en el caso de coeficientes reales [ editar ]
La naturaleza algebraica de las raíces [ editar ]
Cada ecuación cúbica ( 1 ) , ax 3 + bx 2 + cx + d = 0 , con coeficientes reales y un ≠ 0 , tiene tres soluciones (algunos de los cuales puede ser igual el uno al otro si son reales, y dos de los cuales pueden ser complejos números no reales) y al menos una solución real r 1 , esta última afirmación es una consecuencia del teorema del valor intermedio . Si x - r 1 se factoriza fuera del polinomio cúbico, lo que queda es un polinomio cuadrático cuyas raíces r 2 y r3 son raíces de la cúbica; Por la fórmula cuadrática , estas raíces son reales (dando un total de tres raíces reales para el cúbico) o son conjugados complejos , en cuyo caso el cúbico tiene una raíz real y dos no reales.
Se explicó anteriormente cómo usar el signo del discriminante para distinguir entre estos casos. De hecho,
- ( 3 )
porque un cálculo sencillo muestra que
La igualdad ( 3 ) muestra que Δ = 0 si y solo si la ecuación tiene una raíz múltiple. Este no puede ser el caso cuando r 2 y r 3 no son números complejos reales, porque el hecho de que r 1 sea real asegura que r 1 es diferente de r 2 y de r 3 y, por otro lado, el hecho de que r 2 y r 3 no son reales y que cada uno de ellos es el conjugado del otro asegura que r 2 ≠ r 3.
Si r 2 y r 3 no son reales, entonces
Dado que este es el producto de un número real distinto de cero por i , su cuadrado es un número real menor que 0 y, por lo tanto, Δ <0 span=""> . Finalmente, si los números r 1 , r 2 y r 3 son tres números reales distintos, entonces el producto ( r 1 - r 2 ) ( r 1 - r 3 ) ( r 2 - r 3 ) no es un cero real número, y así Δ> 0 .
Interpretación geométrica de las raíces [ editar ]
Tres raíces reales [ editar ]
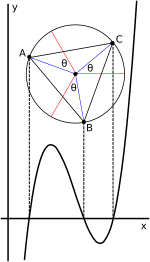
La expresión trigonométrica de las raíces de Viète en el caso de las tres raíces reales se presta a una interpretación geométrica en términos de un círculo. [22] [29]Cuando el cúbico se escribe en forma deprimida ( 2 ) , t 3 + pt + q = 0 , como se muestra arriba, la solución se puede expresar como
aquí Es un ángulo en el círculo unitario; teniendo 13 de ese ángulo corresponde a tomar una raíz cúbica de un número complejo; añadiendo - k 2 π3 para k = 1, 2 encuentra las otras raíces cúbicas; y multiplicando los cosenos de estos ángulos resultantes por corrige la escala.
Para el caso no deprimido ( 1 ) (que se muestra en el gráfico adjunto), el caso deprimido como se indicó anteriormente se obtiene definiendo t tal que x = t - b3 a,así que t = x + b3 a . Gráficamente, esto corresponde a simplemente desplazar el gráfico horizontalmente cuando se cambia entre las variables t y x , sin cambiar las relaciones de ángulo. Este cambio mueve el punto de inflexión y el centro del círculo hacia la y-eje. En consecuencia, las raíces de la ecuación en t suman a cero.
Uno real y dos raíces complejas [ editar ]
En el plano cartesiano [ editar ]
Si se traza una posición cúbica en el plano cartesiano, la raíz real puede verse gráficamente como la intersección horizontal de la curva. Pero además, [30] [31] [32] si las raíces conjugadas complejas se escriben como g ± hi, entonces ges la abscisa (la distancia horizontal positiva o negativa del origen) del punto de tangencia de una línea que es tangente a la curva cúbica e intersecta el eje horizontal en el mismo lugar que la curva cúbica; y h es la raíz cuadrada de la tangente del ángulo entre esta línea y el eje horizontal.
En el plano complejo [ editar ]
Con una raíz real y dos complejas, las tres raíces se pueden representar como puntos en el plano complejo, al igual que las dos raíces de la derivada cúbica. Existe una interesante relación geométrica entre todas estas raíces.
Los puntos en el plano complejo que representan las tres raíces sirven como vértices de un triángulo isósceles. (El triángulo es isósceles porque una raíz está en el eje horizontal (real) y las otras dos raíces, al ser complejos conjugados, aparecen simétricamente por encima y por debajo del eje real). El teorema de Marden dice que los puntos representan las raíces de la derivada del cúbicos son los focos de Steiner en el triángulo, la elipse única que es tangente al triángulo en los puntos medios de sus lados. Si el ángulo en el vértice en el eje real es menor que π3entonces el eje mayor de la elipse se encuentra en el eje real, al igual que sus focos y, por lo tanto, las raíces de la derivada. Si ese ángulo es mayor que π3 , el eje mayor es vertical y sus focos, las raíces de la derivada, son conjugados complejos. Y si ese ángulo es π3 , el triángulo es equilátero, el Steiner inellipse es simplemente el incircle del triángulo, sus focos coinciden entre sí en el incentivo, que se encuentra en el eje real, y por lo tanto el derivado tiene raíces reales duplicadas.
Derivación de las raíces [ editar ]
El método de Cardano [ editar ]
Las soluciones se pueden encontrar con el siguiente método debido a Scipione del Ferro y Tartaglia , publicado por Gerolamo Cardano en 1545 en su libro Ars Magna . Este método se aplica a la depresión cúbica ( 2 ) , t 3 + pt + q = 0 . Introducimos dos variables u y v vinculadas por la condición u + v = t y las sustituimos en la depresión cúbica ( 2 ) , dando
En este punto, Cardano impuso una segunda condición para las variables u y v : 3 uv + p = 0 . A medida que el primer paréntesis se desvanece en la igualdad anterior, obtenemos U 3 + v 3 = - Q y T 3 v 3 = - p 327 de . La combinación de estas dos ecuaciones conduce a una ecuación cuadrática (ya que son la suma y el producto de u 3 y v 3 ). Así u 3 y v 3son las dos raíces de la ecuación cuadrática z 2 + qz - p 327 = 0 . Cardano supone que q 24 + p 327 ≥ 0 . Sugirió que sus lectores consultar a otro de sus libros, De Regula Aliza , que se publicó sólo en 1570, para el caso en el que q 24 + p 327 de <0 font=""> . [33] Resolviendo esta ecuación cuadrática y usando el hecho de que u y v se puede intercambiar, nos encontramos con
- y
Por lo tanto, u + v es igual a:
- ( Fórmula de Cardano )
En su libro L'Algebra , publicado en 1572, Rafael Bombelli explicó que lo que se hizo anteriormente sigue funcionando, con una pequeña diferencia, cuando q 24 + p 327 de <0 font=""> , siempre y cuando uno sabe cómo utilizar los números complejos . [21] La pequeña diferencia se debe al hecho de que un número complejo distinto de cero tiene tres raíces cúbicas y no solo una. Por lo tanto, aunque la igualdad uv = - p3 implica que T 3 v 3 = - p 327 de , esto es , nouna equivalencia. Por lo tanto, no simplemente tomamos ninguna raíz cúbica de
- ( 4 )
y añadirlo a cualquier raíz cúbica de
- ( 5 )
(a menos que uno de ellos sea 0 ); además, eso proporcionaría 9 soluciones a la ecuación ( 2 ) . En cambio, como queremos tener 3 uv = - p , la fórmula de Cardano significa la suma de una raíz cúbica u de ( 4 ) con - p3 u(o, si ( 4 ) es igual a 0 , la suma de un cubo raíz v de ( 5 ) con - p3 v ). Esto solo falla siambosnúmeros(4)y(5)son iguales a 0, en cuyo caso p = q = 0y la fórmula de Cardano simplemente significa t = 3 √ 0 + 3 √ 0 (= 0), que es compatible con el hecho de que, como p = q = 0,(2) sesimplifica a t 3 = 0.
En realidad, no es necesario calcular las tres raíces cúbicas de ( 4 ) . Para ver por qué, dejó ξ = - 12 + 12 √ 3 i . Entonces ξ y ξ (= - 12 - 12 √ 3 i = ξ 2 ) son las raíces cúbicas no real de 1 . Si u es una raíz cúbica de ( 4 ) , y ves una raíz cúbica de (5 ) de modo que 3 uv = - p , entonces las raíces de ( 2 ) son u + v , u + ξ v , y ξ u + ξv , ya que, en cada caso, tenemos la suma de una raíz cúbica de ( 4 ) con una raíz cúbica ( 5 ) y, además, el producto de estas dos raíces es, en cada caso, igual a - p3 .
Tenga en cuenta que ξ 3 = 1 y que ξ 4 = ξ . Así, la fórmula de Cardano, escrita sin ambigüedad para dar las tres raíces, es
donde las raíces cúbicas expresadas como radicales se definen como cualquier par de raíces cúbicas cuyo producto es - p3 . Si p y q son reales y q 24 + p 327 <0 font=""> , esto es lo mismo que exigir que las raíces cúbicas ser complejos conjugados, mientras que si p y q son reales y q 24 + p 327 ≥ 0 , se pueden elegir las raíces cúbicas reales.
La fórmula de Cardano, interpretada de esta manera, es equivalente a la solución general dada anteriormentecuando el coeficiente del término cuadrático es 0 .
Examinaremos ciertos casos particulares. Antes de eso, es conveniente tener en cuenta que, si u es una raíz cúbica de ( 4 ) , si v es una raíz cúbica de ( 5 ) , y si ambos números p y u × v son reales, entonces es automáticamente cierto que u × v = - p3 . Esto es así porque
- ( U × v ) 3 = u 3 × v 3 = q 24 - ( q 24 + p 327 ) = - p 327 = (- p3 ) 3 .
Veamos ahora los casos particulares.
- Si p y q son números reales y q 24 + p 327 de > 0 , dejar que u sea la raíz cúbica real de ( 4 ) y dejar que v sea la raíz cúbica real de ( 5 ) . Entonces u × v = - p3 , porque u × v es real. Entonces, las raíces de la ecuación ( 2 ) son u + v (que es un número real),ξu + ξ v , y ξ u + ξv . Cada una de las raíces segunda y tercera es elconjugado de la otra. Esto puede ser usado para probar que no son reales. De hecho, dos números reales son los conjugados entre sí si y solo si son el mismo número real. Pero
-
- ξu + ξ v = ξ u + ξv ⇔ ( ξ - ξ ) ( u - v ) = 0 ,
- y esta última afirmación es falsa, ya que ξ ≠ ξ y u ≠ v (porque u y v son números reales cuyos cubos son distintos).
- Si p y q son números reales y q 24 + p 327 <0 font=""> , entonces los números ( 4 ) y ( 5 ) son números complejos cada uno de los cuales es el conjugado de la otra. Sea u una raíz cúbica de ( 4 ) y sea v el conjugado de u . Entonces v 3 es el conjugado de u 3 y esto prueba que v 3 es igual a (5 ) . Entonces, nuevamente, como u × v es real, tenemos u × v = - p3 , y por lo tanto las raíces de la ecuación ( 2 ) son u + u , ξu + ξu , y ξ u + ξ u . En este caso, todas las raíces son reales, ya que cada una de ellas es la suma de un número complejo con su conjugado.
- Si p = 0 , entonces las raíces de la ecuación ( 2 ) son las raíces cúbicas de - q . Esto es compatible con la fórmula de Cardano, porque uno de ( 4 ) o ( 5 ) es 0 y el otro es - q .
- Si q = 0 , entonces las raíces de ( 2 ) son 0 y las raíces cuadradas de - p . De nuevo, esto es compatible con la fórmula de Cardano, porque si u es una raíz cuadrada de p / 3 , a continuación, u 3 es una raíz cuadrada de p327 , y esta raíz cuadrada es igual a ( 4 ) o a ( 5 ) , ya que estamos asumiendo que q = 0 . Si v = - ues la otra raíz cuadrada de p / 3 a continuación, por la misma razón, v 3 es igual a ( 4 ) o para ( 5 ) y, además, si u es igual a ( 4 ) a continuación, v es igual a ( 5 ) y vice versa Porque v = - u tenemos u + v = 0 . Por otro lado, ξu + ξ v = ( ξ - ξ ) ×u y así ( ξu + ξ v ) 2 = ( ξ - ξ ) 2 × u 2 = (−3) × p3 = - p , lo que significa queξu + ξ v es una raíz cuadrada de - p . Finalmente, ξ u + ξv = ( ξ - ξ ) × u = - ( ξu + ξ v ) , por lo que debe ser la otra raíz cuadrada de -p .
- Si q 24 + p 327 = 0 (pero p y q no son 0 ), entonces ( 2 ) tiene una raíz simple, que es 3 qp , y una raíz doble , que es - 3 q2 p . Nuevamente, esto es compatible con la fórmula de Cardano. Para ver por qué, en cuenta que afirmar que q 24 + p 327 = 0es equivalente a afirmar que 27 q 24 p 3 = -1 . Si u = v = 3 q2 p , entonces u 3 = v 3 = 27 q 38 p 3 = - q2 y 3 uv = 27 q 24 p 2 = - p . Así, la fórmula de Cardano dice que las raíces de ( 2) son u + v = 2 u = 3 qp , ξu + ξ v = ( ξ + ξ ) × u = - 3 q2 p , y ξ u + ξv = ( ξ + ξ ) × u = - 3 q2 p .
En este último caso (es decir, cuando q 24 + p 327 = 0 , pero p y q no son 0 ), aunque los cálculos hechos anteriormente sugieren que 3 qp es una raíz sencilla de ( 2 ) mientras - 3 q2 p es una raíz doble (que se ha obtenido de dos maneras diferentes), realmente no lo demuestran. Sin embargo, esto puede ser fácilmente confirmado. Solo nota que
desde 27 q 24 p 3 = -1 .
Los números proporcionados por la fórmula de Cardano son soluciones de la ecuación ( 2 ) , pero podría haber otras soluciones además de estas. Sin embargo, esto no ocurre. Vamos u y v ser números tales que T 3 + v 3 = - Q y 3 uv = - p . Para ver que u + v , ξu + ξ v , y ξ u + ξv son las únicas raíces del polinomio t 3 + pt + q, basta notar que
Por lo tanto, t 3 + pt + q = 0 si y solo si t = u + v , t = ξu + ξ v o t = ξ u + ξv .
Sustitución de Vieta [ editar ]
Partiendo de la depresión cúbica ( 2 ) , t 3 + pt + q = 0 , hacemos la sustitución t = w - p3 w , conocida como lasustitución de Vieta . Esto da lugar a la ecuación.
Al multiplicarse por w 3 , se convierte en una ecuación sexual en w , que de hecho es una ecuación cuadrática en w 3 :
- ( 6 )
La fórmula cuadrática permite resolver la ecuación ( 6 ) para w 3 . Si w 1 , w 2 y w 3 son las tres raíces cúbicasde una de las soluciones en w 3 , entonces las raíces del cúbico original deprimido son w 1 - p3 w 1 , w 2 - p3 w 2 , y w 3 - p3w 3 . Otra forma de expresar las raíces es tomarξ= -12 +12 √ 3 i; entonces las raíces del cúbico original deprimido sonw1-p3 w 1 ,ξw1-p3 ξw 1 , y,ξ2w1-p3 ξ 2 w 1 . Este método solo falla cuando ambas raíces de la ecuación(6 ) son iguales a 0 , pero esto solo sucede cuando p = q = 0 , en cuyo caso la única solución de la ecuación ( 2 ) es 0 .
En realidad, la sustitución originalmente utilizada por Vieta (en un texto publicado póstumamente en 1615) fue t = p3 w - w , pero conduce a cálculos similares. [34] Más precisamente, Vieta introdujo una nueva variable w e impuso la condición w ( t + w ) = p3 .
En lo que respecta a las fórmulas, el enfoque de Vieta conduce al mismo resultado que el método de Cardano . Sin embargo, es teóricamente más simple, por dos razones:
- Cada raíz de la ecuación ( 2 ) se expresa desde el principio por una expresión que involucra una sola raíz cúbica. Por lo tanto, no hay ambigüedad como en la fórmula de Cardano .
- Es casi trivial que no haya otras raíces además de las obtenidas por este método. Esto se deduce del hecho de que cualquier número complejo puede escribirse como w - p3 w para algún otro número complejo w .
Método de Lagrange [ editar ]
En su artículo Réflexions sur la résolution algébrique des équations ("Reflexiones sobre la resolución algebraica de ecuaciones"), [35] Joseph Louis Lagrange introdujo un nuevo método para resolver ecuaciones de bajo grado.
Este método funciona bien para las ecuaciones cúbicas y cuárticas , pero Lagrange no logró aplicarlo a una ecuación quíntica , porque requiere resolver un polinomio de grado resolutivo de al menos seis. [36] [37] [38] Esto se explica por el teorema de Abel-Ruffini , que demuestra que tales polinomios no pueden ser resueltos por los radicales. Sin embargo, los métodos modernos para resolver ecuaciones quínticas solubles se basan principalmente en el método de Lagrange. [38]
En el caso de las ecuaciones cúbicas, el método de Lagrange da la misma solución que el de Cardano. Al llamar la atención sobre un problema geométrico que involucra dos cubos de diferente tamaño, Cardano explica en su libro Ars Magna cómo llegó a la idea de considerar lo desconocido de la ecuación cúbica como una suma de otras dos cantidades. El método de Lagrange también se puede aplicar directamente a la ecuación cúbica general ( 1 ) , ax 3 + bx 2 + cx + d = 0 , sin utilizar la reducción a la ecuación cúbica deprimida ( 2 ) , t 3 + pt +q = 0 . Sin embargo, el cálculo es mucho más fácil con esta ecuación reducida.
Supongamos que x 0 , x 1 y x 2 son las raíces de la ecuación ( 1 ) o ( 2 ) , y definir ξ = - 12 + 12 √ 3 i (a raíz cúbica compleja de 1 , es decir, un tercero primitiva raíz de la unidad ) que satisface la relación ξ 2 + ξ + 1 = 0 . Ahora nos ponemos
Esta es la transformada de Fourier discreta de las raíces: observe que mientras que los coeficientes del polinomio son simétricos en las raíces, en esta fórmula se ha elegido un orden en las raíces, por lo que no son simétricos en las raíces. Las raíces pueden entonces recuperarse de los tres s i invirtiendo la transformación lineal anterior mediante la transformada de Fourier discreta inversa, dando
El polinomio s 0 es igual, según las fórmulas de Vieta , a - ba en el caso de la ecuación ( 1 ) y a 0 en el caso de la ecuación ( 2 ) , por lo que solo necesitamos buscar valores para los otros dos.
Los polinomios s 1 y s 2 no son funciones simétricas de las raíces: s 0 es invariante, mientras que las dos permutaciones cíclicas no triviales de las raíces envían s 1 a ξ s 1 y s 2 a ξ 2 s 2 , o s 1 a xi 2 s 1 y s 2 a ξ s 2(dependiendo de la permutación), mientras que la transposición de x 1y x 2 cambia s 1 y s 2 ; otras transposiciones cambian estas sumas y las multiplican por una potencia de ξ .
Así, s 1 3 , s 2 3 y s 1 s 2 quedan invariantes por las permutaciones cíclicas de las raíces, que los multiplican por ξ 3 = 1 . También s 1 s 2 y s 1 3 + s 2 3 quedan invariantes por la transposición de x 1 y x 2, que intercambia s 1 y s 2 . Como el grupo de permutación S 3De las raíces se genera por estas permutaciones, se deduce que s 1 3 + s 2 3 y s 1 s 2 son funciones simétricas de las raíces y, por lo tanto, pueden escribirse como polinomios en los polinomios simétricos elementales y, por lo tanto, como funciones racionales de los coeficientes. de la ecuación. Sea s 1 3 + s 2 3 = A y s 1 s 2 = B en estas expresiones, que se calcularán explícitamente a continuación.
Tenemos que s 1 3 y s 2 3 son las dos raíces de la ecuación cuadrática z 2 - Az + B 3 = 0 . Por lo tanto, la resolución de la ecuación se puede finalizar exactamente como se describe para el método de Cardano, con s 1 y s 2 en lugar de u y v .
Cálculo de A y B [ editar ]
Configurando E 1 = x 0 + x 1 + x 2 , E 2 = x 0 x 1 + x 1 x 2 + x 2 x 0 y E 3 = x 0 x 1 x 2 , los polinomios elementales simétricos, tenemos, usando que ξ 3 = 1 :
La expresión para s 2 3 es la misma con ξ y ξ 2 intercambiados. Por lo tanto, utilizando ξ 2 + ξ = −1 obtenemos
y un cálculo sencillo da
Del mismo modo tenemos
Al resolver la ecuación ( 1 ) tenemos E 1 = - ba , E 2 = ca y E 3 = - da . Con la ecuación ( 2 ) , tenemos E 1 = 0 , E 2 = p y E 3 = - q y por lo tanto A = −27 q and B = −3 p .
Tenga en cuenta que con la ecuación ( 2 ) , tenemos x 0 = 13 ( s 1 + s 2 ) y s 1 s 2 = -3 p , mientras que en el método de Cardano hemos establecido x 0 = u + v y uv = - 13 p . Así tenemos, hasta el intercambio de u y v , s 1 = 3 u y s 2= 3 v . En otras palabras, en este caso, el método de Cardano y el método de Lagrange calculan exactamente las mismas cosas, hasta un factor de tres en las variables auxiliares, siendo la principal diferencia que el método de Lagrange explica por qué estas variables auxiliares aparecen en el problema.
Solución general a la ecuación cúbica con coeficientes arbitrarios [ editar ]
Si estamos tratando con una ecuación cúbica cuyos coeficientes pertenecen a algún campo k (cuya característica es 0 o mayor que 3 ), entonces lo que se hizo anteriormente funciona algebraicamente , con una excepción: los resultados sobre el signo del discriminante , ya que no tienen sentido para los campos generales, aunque el hecho de que la ecuación tenga una raíz múltiple si y solo si Δ = 0 sigue siendo cierto (y por la misma razón). En este caso más general, trabajamos con una extensión K de k en la que cada elemento distinto de cero tiene dos raíces cuadradas y tres raíces cúbicas. Por ejemplo, si k= Q , podemos tomar K = Q , el campo de los números algebraicos .
En particular, todo lo que se hizo anteriormente algebraicamente todavía funciona si k = K = C . Por lo tanto, cada ecuación cúbica con coeficientes complejos tiene una raíz compleja, que es un caso particular del teorema fundamental del álgebra .
En este contexto general, las fórmulas para las raíces en el caso en que Δ = 0 muestran que estas raíces también pertenecen al campo k .
En un campo k cuya característica es 2 o 3 , este enfoque no funciona porque entonces las fórmulas para las raíces dejaron de tener sentido, ya que implican división por 2 y 3 .
Grupos de galois de cúbicos irreductibles [ editar ]
El grupo Galois de un polinomio separable irreducible de grado n es un subgrupo transitivo de S n . En particular, el grupo Galois de un cúbico separable irreducible es un subgrupo transitivo de S 3 y solo hay dos de estos subgrupos: S 3 y A 3 . Hay una forma sencilla de determinar el grupo de Galois de un f ( x ) cúbico irreducible concreto sobre un campo k : es A 3 si el discriminante del cúbico es el cuadrado de un elemento de ky S 3 de locontrario. De hecho, si Δ no es el cuadrado de un elemento de k , entonces k [ √ Δ ] es una extensión del grado 2 de k . Por otro lado, si r 1 , r 2 y r 3 son las raíces de f ( x ) , entonces, dado que la igualdad ( 3 ) se mantiene, es decir, ya que Δ = ( a 2 ( r 1 - r 2 ) (r 1 - r 3 ) ( r 2 - r 3 )) 2 , k [ √ Δ ] ⊂ k [ r 1 , r 2 , r 3 ] , y así, por lafórmula de multiplicatividad para los grados , el grado de k [ r 1 , r 2 , r 3 ] sobre k (es decir, el orden del grupo de Galois de f ( x )) debe ser un múltiplo del grado de k [ √ Δ ] , que es 2 . Por lo tanto, debe ser un número par, por lo que el grupo Galois solo puede ser S 3 .
Por otro lado, si Δ es el cuadrado de un elemento de k , entonces, nuevamente por la igualdad ( 3 ) , tenemos ( r 1 - r 2 ) ( r 1 - r 3 ) ( r 2 - r 3 ) k . Por lo tanto, si σ pertenece al grupo Galois de f ( x ) , entonces σ maps ( r 1 - r 2 ) ( r 1- r 3 ) ( r 2 - r 3 ) en sí mismo. Pero entonces σ no puede actuar en el conjunto { r 1 , r 2 , r 3 } como la transposición que intercambia r 1 y r 2 y deja r 3 fijo, porque entonces σ se mapearía ( r 1 - r 2 ) ( r 1 - r 3 ) ( r 2- r 3 ) en - ( r 1 - r 2 ) ( r 1 - r 3 ) ( r 2 - r 3 ) . Entonces, en este caso, el grupo de Galois de f ( x ) no es S 3 y, por lo tanto, debe ser A 3 .
Se desprende de este criterio de que, si estamos trabajando sobre el campo Q , el grupo de Galois de polinomios cúbicos más irreducibles es S 3 . Un ejemplo de un polinomio cúbico irreducible con coeficientes racionales cuyo grupo de Galois es A 3 es p ( x ) = x 3 - 3 x - 1 , cuyo discriminante es 81 = 9 2 . El polinomio p ( x ) se usa en la prueba estándar de la imposibilidad de triseccionar ángulos arbitrarios usando solo regla y compás.
Colinealidades [ editar ]
Las líneas tangentes a un cúbico en tres puntos colineales interceptan el cúbico nuevamente en los puntos colineales. [39] Esto puede verse como sigue. Si el valor cúbico está definido por f ( x ) = ax 3 + bx 2 + cx + d y si α es un número real, entonces la tangente a la gráfica de f en el punto ( α , f ( α )) es la línea
- {( x , f ( α ) + ( x - α ) f ′ ( α )): x ∈ R }.
Entonces, el punto de intersección entre esta línea y la gráfica de f se puede obtener resolviendo la ecuación f ( x ) = f ( α ) + ( x - α ) f ′ ( α ). Esta es una ecuación cúbica, pero está claro que α es una raíz y, de hecho, una raíz doble, ya que la línea es tangente a la gráfica. La raíz restante es - ba - 2 α . Entonces, el otro punto de intersección entre la línea tangente y la gráfica de f es el punto
Por lo tanto, si P es un punto del gráfico de f , el otro punto de intersección entre la línea tangente en P y el gráfico es el punto A ( P ) , donde A es el mapa definido por
Como A es un mapa afín , si P 1 , P 2 y P 3 son colineales, entonces también lo son los puntos A ( P 1 ) , A ( P 2 ) y A ( P 3 ) .
Simetría [ editar ]
La gráfica de una función cúbica tiene una simetría rotacional o puntual de 180 ° sobre su punto de inflexión. El punto de inflexión de un polinomio cúbico general,
ocurre en un punto ( x 0 , f ( x 0 )) tal que f ′ ′ ( x 0 ) = 0 . Desde f '' ( x ) = 6 ax + 2 b , el punto de inflexión es (- b3 una , 2 b 327 un 2 - bc3 un + d ) . Trasladar la función de modo que el punto de inflexión esté en el origen, se obtiene la función fT definida por:
Como todos los términos son potencias impares de x , f T (- x ) = - f T ( x ), lo que demuestra que todas las funciones cúbicas son simétricas respecto a sus puntos de inflexión. [40]
Aplicaciones [ editar ]
Las ecuaciones cúbicas surgen en otros contextos.
El teorema de Marden establece que los focos de Steiner inellipse de cualquier triángulo se pueden encontrar usando la función cúbica cuyas raíces son las coordenadas en el plano complejo de los tres vértices del triángulo. Las raíces de la primera derivada de este cúbico son las coordenadas complejas de esos focos.
El área de un heptágono regular puede expresarse en términos de las raíces de un cúbico. Además, las relaciones de la diagonal larga al lado, el lado de la diagonal corta y el negativo de la diagonal corta a la diagonal larga satisfacen una ecuación cúbica particular. Además, la relación de inradio y circunradio de un triángulo heptagonal es una de las soluciones de una ecuación cúbica. Los valores de funciones trigonométricas de ángulos relacionados con satisfacer ecuaciones cúbicas.
Dado el coseno (u otra función trigonométrica) de un ángulo arbitrario, el coseno de un tercio de ese ángulo es una de las raíces de un cúbico.
Los valores propios de una matriz de 3 × 3 son las raíces de un polinomio cúbico que es el polinomio característico de la matriz.
La ecuación característica de un lineal de tercer orden ecuación de diferencia o ecuación diferencial es una ecuación cúbica.
En química analítica , la ecuación de Charlot , que se puede usar para encontrar el pH de las soluciones tampón , se puede resolver utilizando una ecuación cúbica.
En la ingeniería química y la termodinámica , las ecuaciones cúbicas de estado se utilizan para modelar el comportamiento de las sustancias (presión, volumen, temperatura) PVT .









































![{\ displaystyle {\ sqrt [{3}] {- {q \ sobre 2} + {\ sqrt {{q ^ {2} \ sobre 4} + {p ^ {3} \ sobre 27}}}}} + {\ sqrt [{3}] {- {q \ sobre 2} - {\ sqrt {{q ^ {2} \ sobre 4} + {p ^ {3} \ sobre 27}}}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c27db1867259741c8811267c8682b5dcffe541b2)
![{\ displaystyle {\ sqrt [{3}] {X}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ab337c088bea120098d3116e3672ab274fef891)






![{\ displaystyle C = {\ sqrt [{3}] {\ frac {\ Delta _ {1} \ pm {\ sqrt {{\ Delta _ {1}} ^ {2} -4 {\ Delta _ {0} } ^ {3}}}} {2}}} {\ text {.}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91120b13d6018115e20cebbdd168cda1d0d59925)




















![{\ displaystyle {\ begin {alineado} & {\ bigl (} a ^ {2} (r_ {1} -r_ {2}) (r_ {1} -r_ {3}) (r_ {2} -r_ { 3}) {\ bigr)} ^ {2} \\ [6pt] = {} & a ^ {4} {\ bigl (} 18 (r_ {1} + r_ {2} + r_ {3}) (r_ { 1} r_ {2} + r_ {1} r_ {3} + r_ {2} r_ {3}) r_ {1} r_ {2} r_ {3} \\ [4pt] & {} - 4 (r_ { 1} + r_ {2} + r_ {3}) ^ {3} r_ {1} r_ {2} r_ {3} + (r_ {1} + r_ {2} + r_ {3}) ^ {2} (r_ {1} r_ {2} + r_ {1} r_ {3} + r_ {2} r_ {3}) ^ {2} \\ [4pt] & {} - 4 (r_ {1} r_ {2 } + r_ {1} r_ {3} + r_ {2} r_ {3}) ^ {3} -27 (r_ {1} r_ {2} r_ {3}) ^ {2} {\ bigr)} \ fin {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9267bc0c3cbba2e648a43dafa2019944c70558ba)

![{\ displaystyle {\ begin {alineado} (r_ {1} -r_ {2}) (r_ {1} -r_ {3}) (r_ {2} -r_ {3}) & = (r_ {1} - r_ {2}) {\ bigl (} r_ {1} - {\ overline {r_ {2}}} {\ bigr)} {\ bigl (} r_ {2} - {\ overline {r_ {2}}} {\ bigr)} \\ [4pt] & = (r_ {1} -r_ {2}) {\ overline {(r_ {1} -r_ {2})}} 2 \ operatorname {Im} (r_ {2 }) i \\ [4pt] & = 2 | r_ {1} -r_ {2} | ^ {2} \ operatorname {Im} (r_ {2}) i \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30934611b0dc2ec53e213ba62af81168239b1c14)







![{\ displaystyle t = {\ sqrt [{3}] {- {q \ sobre 2} + {\ sqrt {{q ^ {2} \ sobre 4} + {p ^ {3} \ sobre 27}}}} } + {\ sqrt [{3}] {- {q \ over 2} - {\ sqrt {{q ^ {2} \ over 4} + {p ^ {3} \ over 27}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d91448198219ff6936ccd3063cc9cb4bb3740fe)


![{\ displaystyle t_ {k} = \ xi ^ {k} {\ sqrt [{3}] {- {q \ sobre 2} + {\ sqrt {{q ^ {2} \ sobre 4} + {p ^ { 3} \ sobre 27}}}}} + \ xi ^ {2k} {\ sqrt [{3}] {- {q \ over 2} - {\ sqrt {{q ^ {2} \ sobre 4} + { p ^ {3} \ sobre 27}}}}}, \ quad k = 0,1,2,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/444461e105d88234126dd33623b35c5e62dafd23)















![{\ displaystyle {\ begin {alineado} & \ left (- {\ frac {b} {a}} - 2 \ alpha, f \ left (- {\ frac {b} {a}} - 2 \ alpha \ right ) \ right) \\ [3pt] = {} & \ left (- {\ frac {b} {a}} - 2 \ alpha, -8a \ alpha ^ {3} -8b \ alpha ^ {2} -2 \ left ({\ frac {b ^ {2}} {a}} + c \ right) \ alpha - {\ frac {bc} {a}} + d \ right) \\ [3pt] = {} & \ izquierda (- {\ frac {b} {a}} - 2 \ alpha, - {\ frac {bc} {a}} + 9d + \ left (6c-2 {\ frac {b ^ {2}} {a} } \ derecha) \ alpha -8f (\ alpha) \ derecha). \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b5c7522947c94b82e989a885740e452b18fd5b4)
![{\ displaystyle {\ begin {alineado} A: \ mathbb {R} ^ {2} & \ longrightarrow \ mathbb {R} ^ {2} \\ [4pt] (x, y) & \ mapsto \ left (- { \ frac {b} {a}} - 2x, - {\ frac {bc} {a}} + 9d + \ left (6c-2 {\ frac {b ^ {2}} {a}} \ right) x- 8y \ right). \ End {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/599c09e42e7715e6a729aca25098c74902d0506b)


No hay comentarios:
Publicar un comentario