ECUACIONES

La ecuación de Antoine es una clase de correlaciones semi-empíricas que describen la relación entre la presión de vapor y la temperatura para componentes puros. La ecuación de Antoine se deriva de la relación de Clausius-Clapeyron . La ecuación fue presentada en 1888 por el ingeniero francés Louis Charles Antoine  [ fr ] (1825–1897). 

Ecuación [ editar ]

La ecuación de Antoine es

$${\ displaystyle \ log _ {10} p = A - {\ frac {B} {C + T}}.

donde p es la presión de vapor, T es la temperatura y A , B y C son constantes específicas del componente.

La forma simplificada con C puesta a cero:

$${\ displaystyle \ log _ {10} p = A - {\ frac {B} {T}}}

Es la ecuación de agosto , después del físico alemán Ernst Ferdinand August (1795–1870). La ecuación de agosto describe una relación lineal entre el logaritmo de la presión y la temperatura recíproca. Esto supone un calor de vaporización independiente de la temperatura . La ecuación de Antoine permite una descripción mejorada, pero aún inexacta, del cambio del calor de vaporización con la temperatura.

La ecuación de Antoine también se puede transformar en una forma de temperatura explícita con manipulaciones algebraicas simples:

$${\ displaystyle T = {\ frac {B} {A- \ log _ {10} \, p}} - C}

Rango de validez [ editar ]

Normalmente, la ecuación de Antoine no se puede usar para describir la curva de presión de vapor saturada completa desde el punto triple hasta el punto crítico , porque no es lo suficientemente flexible. Por lo tanto, los conjuntos de parámetros múltiples para un solo componente se utilizan comúnmente. Se utiliza un conjunto de parámetros de baja presión para describir la curva de presión de vapor hasta el punto de ebullición normal y el segundo conjunto de parámetros se utiliza para el rango desde el punto de ebullición normal hasta el punto crítico.

• Desviaciones típicas de un ajuste de parámetro en todo el rango (datos experimentales para el benceno)
• 

  Desviaciones de una ecuación de agosto ajustada (2 parámetros)
 
• 

  Desviaciones de una ecuación de Antoine ajustada (3 parámetros)
 
• 

  Desviaciones de un ajuste deecuación DIPPR 105 (4 parámetros)

Parámetros de ejemplo [ editar ]

	UNA	segundo	do	T min. DO	T max DO
Agua	7.96681	1730.63	233.426	1	100
Agua	8.14019	1810.94	244.485	99	374
Etanol	8.20417	1642.89	230.300	-57	80
Etanol	7.68117	1332.04	199.200	77	243

Las constantes se dan en ° C y mmHg .

Ejemplo de cálculo [ editar ]

El punto de ebullición normal del etanol es T _B  = 78.32 ° C.

$${\ displaystyle P = 10 ^ {(8 {.} 20417 - {\ frac {1642 {.} 89} {78 {.} 32 + 230 {.} 300}})} = 760 {.} 0 \ \ mathrm {mmHg}}

$${\ displaystyle P = 10 ^ {(7 {.} 68117 - {\ frac {1332 {.} 04} {78 {.} 32 + 199 {.} 200}})} = 761 {.} 0 \ \ mathrm {mmHg}}

(760 mmHg = 101.325 kPa = 1.000 atm = presión normal)

Este ejemplo muestra un problema grave causado por el uso de dos conjuntos diferentes de coeficientes. La presión de vapor descrita no es continua: en el punto de ebullición normal, los dos conjuntos dan resultados diferentes. Esto causa problemas graves para las técnicas computacionales que se basan en una curva de presión de vapor continua.

Son posibles dos soluciones: el primer enfoque utiliza un único conjunto de parámetros de Antoine en un rango de temperatura mayor y acepta la mayor desviación entre las presiones de vapor calculadas y las reales. Una variante de este enfoque de conjunto único es utilizar un conjunto de parámetros especiales ajustado para el rango de temperatura examinado. La segunda solución está cambiando a otra ecuación de presión de vapor con más de tres parámetros. Comúnmente se usan extensiones simples de la ecuación de Antoine (ver más abajo) y las ecuaciones de DIPPR o Wagner. ^[2] [3]

Unidades [ editar ]

Los coeficientes de la ecuación de Antoine se dan normalmente en mmHg, incluso hoy en día, donde se recomienda el SI y se prefieren los pascales . El uso de las unidades pre-SI solo tiene razones históricas y se origina directamente en la publicación original de Antoine.

Sin embargo, es fácil convertir los parámetros a diferentes unidades de presión y temperatura. Para cambiar de grados Celsius a kelvin es suficiente restar 273.15 del parámetro C. Para pasar de milímetros de mercurio a pascales es suficiente agregar el logaritmo común del factor entre ambas unidades al parámetro A:

$${\ displaystyle A _ {\ mathrm {Pa}} = A _ {\ mathrm {mmHg}} + \ log _ {10} {\ frac {101325} {760}} = A _ {\ mathrm {mmHg}} +2.124903.}

Los parámetros para ° C y mmHg para etanol.

UNA	segundo	do
8.20417	1642.89	230.300

se convierten para K y Pa a

UNA	segundo	do
10.32907	1642.89	-42.85

El primer ejemplo de cálculo con T _B = 351.47 K se convierte en

$${\ displaystyle \ log _ {10} (P) = 10 {.} 3291 - {\ frac {1642 {.} 89} {351 {.} 47-42 {.} 85}} = 5 {.} 005727378 = \ log _ {10} (101328 \ \ mathrm {Pa}).}

Se puede usar una transformación igualmente simple si el logaritmo común debe ser intercambiado por el logaritmo natural. Es suficiente multiplicar los parámetros A y B por ln (10) = 2.302585.

El ejemplo de cálculo con los parámetros convertidos (para K y Pa ):

UNA	segundo	do
23.7836	3782.89	-42.85

se convierte en

$${\ displaystyle \ ln P = 23 {.} 7836 - {\ frac {3782 {.} 89} {351 {.} 47-42 {.} 85}} = 11 {.} 52616367 = \ ln (101332 \, \ mathrm {Pa}).}

(Las pequeñas diferencias en los resultados solo se deben a la precisión limitada utilizada de los coeficientes).

Extensión de las ecuaciones de Antoine [ editar ]

Para superar los límites de la ecuación de Antoine, se utiliza una extensión simple mediante términos adicionales:

• $${\ displaystyle P = \ exp {\ left (A + {\ frac {B} {C + T}} + D \ cdot T + E \ cdot T ^ {2} + F \ cdot \ ln \ left (T \ derecha )\Correcto)}}
• $${\ displaystyle P = \ exp \ left (A + {\ frac {B} {C + T}} + D \ cdot \ ln \ left (T \ right) + E \ cdot T ^ {F} \ right).}

Los parámetros adicionales aumentan la flexibilidad de la ecuación y permiten la descripción de toda la curva de presión de vapor. Las formas de la ecuación extendida se pueden reducir a la forma original al establecer los parámetros adicionales D , E y F en 0.

Otra diferencia es que las ecuaciones extendidas usan la e como base para la función exponencial y el logaritmo natural. Esto no afecta la forma de la ecuación.

Fuentes para los parámetros de la ecuación de Antoine [ editar ]

• NIST Química WebBook
• Banco de datos de Dortmund
• Directorio de libros de referencia y bancos de datos que contienen constantes de Antoine
• Varios libros de referencia y publicaciones, por ejemplo,
• El manual de química de Lange, McGraw-Hill Professional
• Wichterle I., Linek J., "Constantes de presión de vapor de Antoine de compuestos puros"
• Yaws CL, Yang H.-C., "Para estimar fácilmente la presión de vapor. Los coeficientes de antoína relacionan la presión de vapor con la temperatura para casi 700 compuestos orgánicos importantes", Procesamiento de hidrocarburos, 68 (10), páginas 65–68, 1989

la ley de Archie relaciona la conductividad eléctrica in situ de una roca sedimentaria con su porosidad y saturación de salmuera :

$${\ displaystyle C_ {t} = {\ frac {1} {a}} C_ {w} \ phi ^ {m} S_ {w} ^ {n}}

Aquí, $${\ displaystyle \ phi \, \!} denota la porosidad, $${\ displaystyle C_ {t}} La conductividad eléctrica del fluido saturado de roca. $${\ displaystyle C_ {w}} Representa la conductividad eléctrica de la salmuera. $${\ displaystyle S_ {w}}es la saturación de salmuera ,$${\ displaystyle m} es el exponente de cementación de la roca (generalmente en el rango de 1.8 a 2.0 para las areniscas), $${\ displaystyle n} es el exponente de saturación (generalmente cerca de 2) y $${\ displaystyle a}Es el factor de tortuosidad .

Reformulado para resistividad eléctrica , se lee la ecuación.

$${\ displaystyle R_ {t} = a \ phi ^ {- m} S_ {w} ^ {- n} R_ {w}}

con $${\ displaystyle R_ {t}} por el fluido saturado de resistividad de roca, y $${\ displaystyle R_ {w}} Por la resistividad de la salmuera.

El factor

$${\ displaystyle F = {\ frac {a} {\ phi ^ {m}}} = {\ frac {R_ {o}} {R_ {w}}}}

También se le llama factor de formación , donde$${\ displaystyle R_ {o}} es la resistividad de la roca llena de agua solamente ($${\ displaystyle S_ {w} = 1}).

El factor

$${\ displaystyle I = {\ frac {R_ {t}} {R_ {o}}} = S_ {w} ^ {- n}}

También se le llama el índice de resistividad .

Es una ley puramente empírica que intenta describir el flujo de iones (principalmente sodio y cloruro ) en arenas limpias y consolidadas, con una porosidad intergranular variable. Se supone que la conducción eléctrica no está presente dentro de los granos de roca o en otros fluidos que no sean agua.

La ley de Archie lleva el nombre de Gus Archie (1907–1978) quien desarrolló esta relación cuantitativa empírica entre la porosidad, la conductividad eléctrica y la saturación de salmuera de las rocas. La ley de Archie sentó las bases para la interpretación moderna de los registros de pozos, ya que relaciona las mediciones de conductividad eléctrica de los pozos con las saturaciones de hidrocarburos (que, para la roca saturada de fluido, es igual a$${\ displaystyle 1-S_ {w}}).










ecuación de Arrhenius es una fórmula para la dependencia de la temperatura de las velocidades de reacción . La ecuación fue propuesta por Svante Arrhenius en 1889, basada en el trabajo del químico holandés Jacobus Henricus van 't Hoff quien notó en 1884 que la ecuación de van' t Hoff para la dependencia de la temperatura de las constantes de equilibrio sugiere tal fórmula para las tasas de ambos. Reacciones hacia adelante y hacia atrás. Esta ecuación tiene una vasta e importante aplicación para determinar la tasa de reacciones químicas y para el cálculo de la energía de activación. Arrhenius proporcionó una justificación física e interpretación para la fórmula. ^[1] [2][3] Actualmente, se ve mejor como unarelación empírica . ^[4] : 188 Puede usarse para modelar la variación de temperatura de los coeficientes de difusión, la población de vacantes de cristales, las tasas de fluencia y muchos otros procesos / reacciones inducidas térmicamente. Laecuación de Eyring , desarrollada en 1935, también expresa la relación entre la velocidad y la energía.

Ecuación [ editar ]

En casi todos los casos prácticos, $${\ displaystyle E_ {a} \ gg RT}y k aumenta rápidamente con T .

Matemáticamente, a muy altas temperaturas para que $${\ displaystyle E_ {a} \ ll RT}, knivela y se acerca a A como límite, pero este caso no ocurre en condiciones prácticas.

La ecuación de Arrhenius da la dependencia de la constante de velocidad de una reacción química en la temperatura absoluta , un factor pre-exponencial y otras constantes de la reacción.

$${\ displaystyle k = Ae ^ {\ frac {-E _ {\ rm {a}}} {RT}},}

dónde

k es la constante de velocidad ,

T es la temperatura absoluta (en kelvins ),

A es el factor pre-exponencial , una constante para cada reacción química. Según la teoría de colisiones , A es la frecuencia de colisiones en la orientación correcta,

E _a es la energía de activación para la reacción (en las mismas unidades que RT ),

R es la constante de gas universal . ^{[1] [2] [3]}

Alternativamente, la ecuación se puede expresar como

$${\ displaystyle k = Ae ^ {\ frac {-E _ {\ rm {a}}} {k _ {\ rm {B}} T}},}

dónde

E _a es la energía de activación para la reacción (en las mismas unidades que k _B T ),

k _B es la constante de Boltzmann .

La única diferencia es la unidad de energía de E _a : la primera forma usa energía por mol , que es común en química, mientras que la última forma usa energía por molécula directamente, lo cual es común en física. Las diferentes unidades se contabilizan en el uso de ya sea la constante de los gases , R , o la constante de Boltzmann , k _B , como el multiplicador de la temperatura T .

Las unidades del factor preexponencial A son idénticas a las de la constante de velocidad y variarán según el orden de la reacción. Si la reacción es de primer orden, tiene las unidades: s ⁻¹ , y por esa razón a menudo se le llama factor de frecuencia o frecuencia de intento de la reacción. Más simple, k es el número de colisiones que resultan en una reacción por segundo, A es el número de colisiones (que llevan a una reacción o no) por segundo que ocurren con la orientación adecuada para reaccionar ^[5] y$${\ displaystyle e ^ {- E _ {\ rm {a}} / (RT)}}es la probabilidad de que cualquier colisión dada resulte en una reacción. Se puede observar que aumentar la temperatura o disminuir la energía de activación (por ejemplo, mediante el uso de catalizadores ) resultará en un aumento de la velocidad de reacción.

Dado el pequeño rango de temperatura de los estudios cinéticos, es razonable aproximar la energía de activación como independiente de la temperatura. De manera similar, bajo un amplio rango de condiciones prácticas, la dependencia de la temperatura débil del factor pre-exponencial es despreciable en comparación con la dependencia de la temperatura de la temperatura$${\ displaystyle \ exp (-E _ {\ rm {a}} / (RT))}factor; Excepto en el caso de reacciones limitadas por difusión "sin barreras" , en cuyo caso el factor pre-exponencial es dominante y es directamente observable.

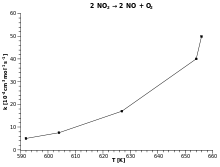
Arrhenius parcela [ editar ]

Artículo principal: trama de Arrhenius

Arrhenius trama lineal: ln  k frente a 1 / T .

Tomando el logaritmo natural de la ecuación de Arrhenius se obtienen:

$${\ displaystyle \ ln k = \ ln A - {\ frac {E _ {\ rm {a}}} {R}} {\ frac {1} {T}}.

Reorganizar los rendimientos:

$${\ displaystyle \ ln k = {\ frac {-E _ {\ rm {a}}} {R}} \ left ({\ frac {1} {T}} \ right) + \ ln A.}

Esto tiene la misma forma que una ecuación para una línea recta:

$${\ displaystyle y = mx + b,}

donde x es el recíproco de t .

Por lo tanto, cuando una reacción tiene una constante de velocidad que obedece a la ecuación de Arrhenius, una gráfica de ln  k frente a T ^-1 da una línea recta, cuya pendiente y la intersección puede ser utilizado para determinar E _una y A . Este procedimiento se ha vuelto tan común en la cinética química experimental que los profesionales han optado por usarlo para definir la energía de activación de una reacción. Es decir, la energía de activación se define como (- R ) multiplicada por la pendiente de una gráfica de ln  k vs. (1 / T ):

$${\ displaystyle E _ {\ rm {a}} \ equiv -R \ left [{\ frac {\ partial \ ln k} {\ partial (1 / T)}} \ right] _ {P}.}

Ecuación de Arrhenius Modificado [ editar ]

La ecuación de Arrhenius modificada ^[6] hace explícita la dependencia de la temperatura del factor pre-exponencial. La ecuación modificada suele ser de la forma.

$${\ displaystyle k = AT ^ {n} e ^ {- E _ {\ rm {a}} / (RT)}.

La expresión de Arrhenius original anterior corresponde a n  = 0. Las constantes de velocidad ajustadas normalmente se encuentran en el rango −1 < n <1 font=""> . Los análisis teóricos dan varias predicciones para n . Se ha señalado que "no es factible establecer, sobre la base de los estudios de temperatura de la constante de velocidad, si la dependencia T ^1/2 predicha del factor pre-exponencial se observa experimentalmente". ^[4] : 190 Sin embargo, si hay evidencia adicional disponible, de la teoría y / o del experimento (como la dependencia de la densidad), no hay obstáculos para las pruebas incisivas de la ley de Arrhenius.

Otra modificación común es la forma exponencial estirada ^{[ cita requerida ]}

$${\ displaystyle k = A \ exp \ left [- \ left ({\ frac {E_ {a}} {RT}} \ right) ^ {\ beta} \ right],

donde β es un número sin dimensiones de orden 1. Esto generalmente se considera una corrección puramente empírica o un factor de fusión para que el modelo se ajuste a los datos, pero puede tener un significado teórico, por ejemplo, que muestra la presencia de un rango de energías de activación o en especial Casos como el salto de rango variable de Mott .

Interpretación teórica de la ecuación [ editar ]

Concepto de energía de activación de Arrhenius [ editar ]

Arrhenius argumentó que para que los reactivos se transformen en productos, primero deben adquirir una cantidad mínima de energía, llamada energía de activación E _a . A una temperatura absoluta T , la fracción de moléculas que tienen una energía cinética mayor que E _a puede calcularse a partir de la mecánica estadística . El concepto de energía de activación explica la naturaleza exponencial de la relación, y de una forma u otra, está presente en todas las teorías cinéticas.

Los cálculos para las constantes de velocidad de reacción implican un promedio de energía sobre una distribución de Maxwell-Boltzmann con$${\ displaystyle E _ {\ rm {a}}}como límite inferior y, por lo tanto, a menudo son del tipo de funciones gamma incompletas , que resultan ser proporcionales a$${\ displaystyle e ^ {\ frac {-E _ {\ rm {a}}} {RT}}}.

Teoría de la colisión [ editar ]

Artículo principal: Teoría de colisiones.

Un ejemplo proviene de la teoría de colisiones de las reacciones químicas, desarrollada por Max Trautz y William Lewis en los años 1916–18. En esta teoría, se supone que las moléculas reaccionan si chocan con una energía cinética relativa a lo largo de sus líneas de centro que excede a E _a . Esto conduce a una expresión muy similar a la ecuación de Arrhenius.

La teoría del estado de transición [ editar ]

La ecuación de Eyring , otra expresión similar a Arrhenius, aparece en la " teoría del estado de transición " de las reacciones químicas, formulada por Wigner , Eyring , Polanyi y Evans en la década de 1930. Esto toma varias formas, pero una de las más comunes es

$${\ displaystyle k = {\ frac {k _ {\ rm {B}} T} {h}} e ^ {- {\ frac {\ Delta G ^ {\ ddagger}} {RT}}},}

dónde $${\ displaystyle \ Delta G ^ {\ ddagger}}Es la energía de activación de Gibbs .$${\ displaystyle k _ {\ rm {B}}}es la constante de Boltzmann , y$${\ displaystyle h}Es la constante de Planck.

A primera vista, esto parece un exponencial multiplicado por un factor que es lineal en temperatura. Sin embargo, la energía libre es en sí misma una cantidad dependiente de la temperatura. La energía libre de activación es la diferencia de un término de entalpía y un término de entropía multiplicado por la temperatura absoluta. Cuando todos los detalles se resuelven, uno termina con una expresión que nuevamente toma la forma de un exponencial de Arrhenius multiplicado por una función de T que varía lentamente . La forma precisa de la dependencia de la temperatura depende de la reacción, y puede calcularse utilizando fórmulas de la mecánica estadística que involucran las funciones de partición de los reactivos y del complejo activado.

Limitaciones de la idea de la energía de activación de Arrhenius [ editar ]

Tanto la energía de activación de Arrhenius como la constante de velocidad k están determinadas experimentalmente y representan parámetros macroscópicos específicos de la reacción que no están simplemente relacionados con las energías de umbral y el éxito de las colisiones individuales a nivel molecular. Considere una colisión particular (una reacción elemental) entre las moléculas A y B. El ángulo de colisión, la energía de traslación relativa, la energía interna (particularmente vibratoria) determinarán la posibilidad de que la colisión produzca una molécula de producto AB. Mediciones macroscópicas de E y Kson el resultado de muchas colisiones individuales con diferentes parámetros de colisión. Para probar las velocidades de reacción a nivel molecular, los experimentos se llevan a cabo en condiciones cercanas a la colisión y este sujeto a menudo se llama dinámica de reacción molecular. ^[7]

Hay desviaciones de la ley de Arrhenius durante la transición de vidrio en todas las clases de materia de formación de vidrio. ^[8] La ley de Arrhenius predice que el movimiento de las unidades estructurales (átomos, moléculas, iones, etc.) debería disminuir a una velocidad más lenta a través de la transición vítrea que la observada experimentalmente. En otras palabras, las unidades estructurales se ralentizan a un ritmo más rápido de lo que predice la ley de Arrhenius. Esta observación se hace razonable suponiendo que las unidades deben superar una barrera de energía mediante una energía de activación térmica. La energía térmica debe ser lo suficientemente alta como para permitir el movimiento de traslación de las unidades, lo que conduce a un flujo viscoso del material.