EL PROCESAMIENTO DE IMÁGENES

Este artículo puede requerir una limpieza para cumplir con los estándares de calidad de Wikipedia . El problema específico es: los fragmentos grandes del artículo son incoherentes. Parece ser una mezcla de pensamientos recopilados y pensamientos a medias sobre diversos temas. Por favor, ayuda a mejorar este artículo si puedes. ( Febrero de 2019 )( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

Un selfie 3D a escala 1:20 impreso por Shapeways usando impresión basada en yeso, creado por el parque en miniatura Madurodam a partir de imágenes en 2D tomadas en su fotomatón de Fantasitron.

Los modelos en 3D se generan a partir de imágenes en 2D tomadas en el fotomatón de Fantasitron 3D en Madurodam

Generación y reconstrucción de formas 3D a partir de siluetas o mapas de profundidad de vista única o múltiple ^[1]

La reconstrucción en 3D a partir de múltiples imágenes es la creación de modelos tridimensionales apartir de un conjunto de imágenes. Es el proceso inverso de obtener imágenes en 2D de escenas en 3D.

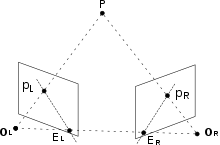
La esencia de una imagen es una proyección desde una escena 3D a un plano 2D, durante el cual se pierde la profundidad del proceso. El punto 3D correspondiente a un punto de imagen específico está restringido para estar en la línea de visión. Desde una sola imagen, es imposible determinar qué punto en esta línea corresponde al punto de la imagen. Si hay dos imágenes disponibles, entonces la posición de un punto 3D se puede encontrar como la intersección de los dos rayos de proyección. Este proceso se conoce como triangulación . La clave para este proceso son las relaciones entre las vistas múltiples que transmiten la información de que los conjuntos de puntos correspondientes deben contener alguna estructura y que esta estructura está relacionada con las poses y la calibración de la cámara.

En las últimas décadas, existe una importante demanda de contenido 3D para gráficos de computadora , realidad virtual y comunicación, lo que provoca un cambio en el énfasis de los requisitos. Muchos sistemas existentes para la construcción de modelos 3D se construyen alrededor de hardware especializado (por ejemplo, equipos estéreo), lo que resulta en un alto costo, que no puede satisfacer los requisitos de sus nuevas aplicaciones. Esta brecha estimula el uso de las instalaciones de imágenes digitales (como una cámara). La ley de Moore también nos dice que se puede hacer más trabajo en software. Un método temprano fue propuesto por Tomasi y Kanade. ^[2] Usaron un enfoque de factorización afín para extraer 3D de secuencias de imágenes. Sin embargo, el supuesto de proyección ortográfica es una limitación significativa de este sistema.

Procesando [ editar ]

Un casco visual puede ser reconstruido a partir de múltiples siluetas de un objeto. ^[3]

La tarea de convertir varias imágenes 2D en un modelo 3D consiste en una serie de pasos de procesamiento:

La calibración de la cámara consta de parámetros intrínsecos y extrínsecos, sin los cuales, en algún nivel, no puede funcionar ningún arreglo de algoritmos. La línea de puntos entre la determinación de Calibración y Profundidad representa que la calibración de la cámara generalmente se requiere para determinar la profundidad.

La determinación de la profundidad sirve como la parte más difícil en todo el proceso, ya que calcula el componente 3D que falta en cualquier imagen dada: la profundidad. El problema de la correspondencia , encontrar coincidencias entre dos imágenes para que la posición de los elementos coincidentes se puedan triangular en el espacio 3D es la cuestión clave aquí.

Una vez que tenga los múltiples mapas de profundidad , debe combinarlos para crear una malla final mediante el cálculo de la profundidad y la proyección fuera de la cámara: registro . La calibración de la cámara se utilizará para identificar dónde se pueden combinar las muchas mallas creadas por los mapas de profundidad para desarrollar una más grande, proporcionando más de una vista para la observación.

En la etapa de Aplicación de materiales , tiene una malla 3D completa, que puede ser el objetivo final, pero generalmente querrá aplicar el color de las fotografías originales a la malla. Esto puede abarcar desde proyectar las imágenes en la malla de forma aleatoria, pasando por enfoques de combinación de texturas para una súper resolución y, finalmente, segmentar la malla por material, como propiedades especulares y difusas.

Descripción matemática de la reconstrucción [ editar ]

Dado un conjunto de puntos 3D vistos por N cámaras con matrices. $${\ displaystyle \ {P ^ {i} \} _ {i = 1 \ ldots N}}. Definir$${\ displaystyle m_ {j} ^ {i} \ simeq P ^ {i} w_ {j}} Ser las coordenadas homogéneas de la proyección de la $${\ displaystyle j ^ {th}} apuntar a la $${\ displaystyle i ^ {th}}cámara. El problema de reconstrucción se puede cambiar a: dado el grupo de coordenadas de píxeles$${\ displaystyle \ {m_ {j} ^ {i} \}}, encuentra el conjunto correspondiente de matrices de cámara. $${\ displaystyle \ {P ^ {i} \}} y la estructura de la escena $${\ displaystyle \ {w_ {j} \}} tal que

$${\ displaystyle m_ {j} ^ {i} \ simeq P ^ {i} w_ {j}} (1)

Generalmente, sin más restricciones, obtendremos una reconstrucción proyectiva. ^[4] [5] Si$${\ displaystyle \ {P ^ {i} \}} y $${\ displaystyle \ {w_ {j} \}}satisfacer (1), $${\ displaystyle \ {P ^ {i} T \}} y $${\ displaystyle \ {T ^ {- 1} w_ {j} \}}satisfará (1) con cualquier matriz T no singular 4 × 4 .

Una reconstrucción proyectiva se puede calcular únicamente por la correspondencia de puntos, sin ninguna información a priori.

Autocalibración [ editar ]

La autocalibración o autocalibración es el enfoque clásico, en el que el movimiento y los parámetros de la cámara se recuperan primero, utilizando rigidez, luego la estructura se calcula fácilmente. Dos métodos para implementar esta idea se presentan a continuación:

Ecuaciones de Kruppa [ editar ]

Con un mínimo de tres desplazamientos, podemos obtener los parámetros internos de la cámara utilizando un sistema de ecuaciones polinomiales debido a Kruppa, ^[6] que se derivan de una interpretación geométrica de la restricción de rigidez. ^[7] [8]

La matriz $${\ displaystyle K = AA ^ {\ top}}Se desconoce en las ecuaciones de Kruppa, denominada matriz de coeficientes de Kruppa. Con K y con el método de factorización de Cholesky se pueden obtener fácilmente los parámetros intrínsecos:

{\ displaystyle K = {\ begin {bmatrix} k_ {1} & k_ {2} & k_ {3} \\ k_ {2} & k_ {4} & k_ {5} \\ k_ {3} & k_ {5} & 1 \\ \ end {bmatrix}}}

Recientemente Hartley ^[9] propuso una forma más simple. Dejar$${\ displaystyle F} ser escrito como $${\ displaystyle F = DUV ^ {\ top}}, dónde

Luego se reescriben las ecuaciones de Kruppa (la derivación se puede encontrar en ^[9] )

Mendonça y Cipolla [ editar ]

Este método se basa en el uso de la restricción de rigidez. Diseñe una función de costo, que considere los parámetros intrínsecos como argumentos y las matrices fundamentales como parámetros.$${\ displaystyle {F} _ {i} j} Se define como la matriz fundamental, $${\ displaystyle {A} _ {i}}y $${\ displaystyle {A} _ {j}} Como matrices de parámetros intrínsecos.

La estratificación [ editar ]

Recientemente, se han propuesto nuevos métodos basados ​​en el concepto de estratificación . A partir de una estructura proyectiva, que se puede calcular solo a partir de correspondencias, actualice esta reconstrucción proyectiva a una reconstrucción euclidiana, haciendo uso de todas las restricciones disponibles. Con esta idea, el problema se puede estratificar en diferentes secciones: según la cantidad de restricciones disponibles, se puede analizar a un nivel diferente, proyectivo, afín o euclidiano.

La estratificación de la geometría 3D [ editar ]

Por lo general, el mundo se percibe como un espacio euclidiano en 3D . En algunos casos, no es posible utilizar la estructura euclidiana completa del espacio 3D. El más simple es proyectivo, luego la geometría afín que forma las capas intermedias y finalmente la geometría euclidiana. El concepto de estratificación está estrechamente relacionado con la serie de transformaciones en entidades geométricas: en el estrato proyectivo hay una serie de transformaciones proyectivas (una homografía ), en el estrato afín hay una serie de transformaciones afines y en el estrato euclidiano una serie de Transformaciones euclidianas.

Supongamos que una escena fija es capturada por dos o más cámaras en perspectiva y las correspondencias entre puntos visibles en diferentes imágenes ya están dadas. Sin embargo, en la práctica, el emparejamiento es un tema esencial y extremadamente desafiante en la visión de computadora. Aquí, suponemos que$${\ displaystyle n} Puntos 3D $${\ displaystyle A_ {i}} son observados por $${\ displaystyle m} Cámaras con matrices de proyección. $${\ displaystyle P_ {j}, j = 1, \ ldots, m.}Ni las posiciones de punto ni la proyección de cámara son conocidas. Solo las proyecciones$${\ displaystyle a_ {ij}} del $${\ displaystyle i ^ {th}} punto en el $${\ displaystyle j ^ {th}} Las imágenes son conocidas.

La reconstrucción proyectiva [ editar ]

El conteo simple indica que tenemos $${\ displaystyle 2nm} mediciones independientes y solo $${\ displaystyle 11m + 3n}incógnitas, por lo que se supone que el problema es soluble con suficientes puntos e imágenes. Las ecuaciones en coordenadas homogéneas se pueden representar:

$${\ displaystyle a_ {ij} \ sim P_ {j} A_ {i} \ qquad i = 1, \ ldots n, ~~ j = 1, \ ldots m} (2)

Así que podemos aplicar una singular 4 × 4 transformación H de las proyecciones$${\ displaystyle P_ {j}}→$${\ displaystyle P_ {j} H ^ {- 1}} y puntos del mundo $${\ displaystyle A_ {i}}→$${\ displaystyle HA_ {i}}. Por lo tanto, sin más restricciones, la reconstrucción es solo una deformación proyectiva desconocida del mundo 3D.

La reconstrucción afín [ editar ]

Consulte el espacio afín para obtener información más detallada sobre cómo calcular la ubicación del avión en el infinito$${\ displaystyle {\ Pi} _ {\ infty}}. La forma más sencilla es explotar el conocimiento previo, por ejemplo, la información de que las líneas en la escena son paralelas o que un punto es el tercio entre otros dos.

También podemos utilizar restricciones previas en el movimiento de la cámara. Al analizar diferentes imágenes del mismo punto se puede obtener una línea en la dirección del movimiento. La intersección de varias líneas es el punto en el infinito en la dirección del movimiento y una restricción en la estructura afín.

La reconstrucción de Euclides [ editar ]

Al mapear la reconstrucción proyectiva a una que satisface un grupo de restricciones euclidianas redundantes, podemos encontrar una transformación proyectiva H en la ecuación (2). Las ecuaciones son altamente no lineales y se requiere una buena estimación inicial de la estructura. Esto se puede obtener asumiendo una proyección lineal - proyección paralela, que también permite una fácil reconstrucción por descomposición de la SVD. ^[2]

Algebraic vs error geométrico [ editar ]

Inevitablemente, los datos medidos (es decir, las posiciones de imagen o puntos mundiales) son ruidosos y el ruido proviene de muchas fuentes. Para reducir el efecto del ruido, usualmente usamos más ecuaciones de las necesarias y resolvemos con los mínimos cuadrados .

Por ejemplo, en una formulación típica de problema de espacio nulo Ax = 0 (como el algoritmo DLT), el cuadrado del residual || Axe || Se está minimizando con el método de mínimos cuadrados.

En general, si || Hacha || se puede considerar como una distancia entre las entidades geométricas (puntos, líneas, planos, etc.), entonces lo que se minimiza es un error geométrico , de lo contrario (cuando el error carece de una buena interpretación geométrica) se denomina error algebraico .

Por lo tanto, en comparación con el error algebraico, preferimos minimizar un error geométrico por las razones enumeradas:

1. La cantidad que se minimiza tiene un significado.
2. La solución es más estable.
3. La solución es constante bajo transformaciones euclidianas.

Todos los algoritmos lineales (DLT y otros) que hemos visto hasta ahora minimizan un error algebraico. En realidad, no hay justificación para minimizar un error algebraico aparte de la facilidad de implementación, ya que resulta en un problema lineal. La minimización de un error geométrico es a menudo un problema no lineal, que admite solo soluciones iterativas y requiere un punto de partida.

Por lo general, la solución lineal basada en residuos algebraicos sirve como punto de partida para una minimización no lineal de una función de costo geométrico, que proporciona a la solución un "pulido" final. ^[10]

Reconstrucción 3D de Imágenes Médicas [ editar ]

Motivación y aplicaciones [ editar ]

Las imágenes 2-D tienen problemas de anatomía que se superponen entre sí y no revelan las anomalías. La imagen tridimensional se puede utilizar para fines diagnósticos y terapéuticos.

Los modelos 3-D se utilizan para planificar la operación, los estudios morfométricos y tienen más confiabilidad en ortopedia.

Proyección de P en ambas cámaras.

Enunciado del problema y conceptos básicos [ editar ]

Para reconstruir imágenes en 3-D a partir de imágenes en 2-D tomadas por una cámara en múltiples ángulos. Las técnicas de imagenología médica como la tomografía computarizada y la resonancia magnética son costosas, y aunque las tomografías computarizadas son precisas, pueden inducir altas dosis de radiación, lo que es un riesgo para los pacientes con ciertas enfermedades. Los métodos basados ​​en la resonancia magnética no son precisos. Dado que estamos expuestos a poderosos campos magnéticos durante una exploración de MRI, este método no es adecuado para pacientes con implantes metálicos ferromagnéticos. Ambos métodos se pueden hacer solo cuando está en posición acostada donde cambia la estructura global del hueso. Por lo tanto, discutimos los siguientes métodos que se pueden realizar mientras está de pie y requiere una dosis de radiación baja.

Aunque estas técnicas son imágenes tridimensionales, la región de interés se restringe a una porción; Los datos se adquieren para formar una secuencia de tiempo.

1) Técnica estéreo basada en puntos correspondientes [ editar ]

Este método es simple e implementado al identificar los puntos manualmente en radiografías de vista múltiple. El primer paso es extraer los puntos correspondientes en dos imágenes de rayos X y el segundo paso es la reconstrucción en 3D con algoritmos como Transformada lineal discreta. ^[11] Usando DLT, la reconstrucción se realiza solo donde hay SCP. Al aumentar el número de puntos, los resultados mejoran ^[12] pero consumen mucho tiempo. Este método tiene baja precisión debido a la baja reproducibilidad y el consumo de tiempo. Este método depende de la habilidad del operador. Este método no es adecuado para estructuras óseas con forma continua. Este método se utiliza generalmente como una solución inicial para otros métodos. ^[13]

2) Método de contorno correspondiente no estéreo (NCSS) [ editar ]

Este método utiliza imágenes de rayos X para la reconstrucción 3D y para desarrollar modelos 3D con bajas dosis de radiación en posiciones de soporte de peso.

En el algoritmo NSCC, el paso preliminar es el cálculo de una solución inicial. En primer lugar se definen las regiones anatómicas del objeto genérico. En segundo lugar, se realiza la identificación manual de los contornos 2D en las radiografías. Desde cada radiografía se generan contornos 2D utilizando el objeto de solución inicial 3D. Los contornos 3D de la superficie del objeto inicial se proyectan en su radiografía asociada. ^[13] La asociación 2D realizada entre estos 2 puntos de ajuste se basa en distancias de punto a punto y derivaciones de contornos, desarrollando una correspondencia entre los contornos 2D y los contornos 3D. El siguiente paso es la optimización de la solución inicial. Por último, la deformación de la solución optimizada se realiza aplicando el algoritmo Kriging a la solución optimizada. ^[14] Finalmente, al iterar el paso final hasta que la distancia entre dos puntos de ajuste sea superior a un valor de precisión dado, se obtiene el objeto reconstruido.

La ventaja de este método es que se puede usar para estructuras óseas con forma continua y también reduce la intervención humana, pero consumen mucho tiempo.

3) Técnica de representación de superficie [ editar ]

La técnica de Representación de superficies visualiza un objeto 3D como un conjunto de superficies llamadas superficies iso. Cada superficie tiene puntos con la misma intensidad (llamada valor iso). Se usa cuando queremos ver las estructuras separadas, por ejemplo, el cráneo de las rodajas de la cabeza, el sistema de vasos sanguíneos de las rodajas del cuerpo, etc. Esta técnica se utiliza principalmente para datos de alto contraste. Dos métodos principales para la reconstrucción son:

• Reconstrucción basada en el contorno: los contornos iso se unen para formar iso-superficies ^[15]
• Reconstrucción basada en vóxels: los vóxeles que tienen los mismos valores de intensidad se utilizan para formar superficies iso. Un algoritmo popular es Marching Cubes. ^[15] Algunos algoritmos similares como Marching Tetrahedrons, Dividing Cubes ^[15] pueden considerarse.

Otras técnicas propuestas o desarrolladas incluyen métodos basados ​​en modelos de formas estadísticas, métodos paramétricos, métodos híbridos.