EL PROCESAMIENTO DE IMÁGENES

La ecualización adaptativa de histograma (AHE) es una técnica de procesamiento de imágenes porcomputadora que se utiliza para mejorar el contraste en las imágenes. A diferencia de la ecualización de histogramas ordinaria, el método adaptativo calcula varios histogramas , cada uno correspondiente a una sección distinta de la imagen, y los utiliza para redistribuir los valores de luminosidad de la imagen. Por lo tanto, es adecuado para mejorar el contraste local y mejorar las definiciones de bordes en cada región de una imagen.

Sin embargo, AHE tiene una tendencia a amplificar demasiado el ruido en regiones relativamente homogéneas de una imagen. Una variante de la ecualización de histograma adaptativa denominada ecualización de histograma adaptativa limitada por contraste (CLAHE) evita esto al limitar la amplificación.

La motivación y la explicación del método [ editar ]

La ecualización de histograma ordinaria utiliza la misma transformación derivada del histograma de imagen para transformar todos los píxeles. Esto funciona bien cuando la distribución de valores de píxeles es similar en toda la imagen. Sin embargo, cuando la imagen contiene regiones que son significativamente más claras o más oscuras que la mayoría de la imagen, el contraste en esas regiones no será lo suficientemente mejorado.

La ecualización adaptativa del histograma (AHE) mejora esto al transformar cada píxel con una función de transformación derivada de una región vecina. Fue desarrollado por primera vez para su uso en pantallas de cabina de aviones. ^{[1] citado en [2]} En su forma más simple, cada píxel se transforma en función del histograma de un cuadrado que rodea al píxel, como se muestra en la siguiente figura. La derivación de las funciones de transformación de los histogramas es exactamente la misma que para la ecualización ordinaria de histogramas : la función de transformación es proporcional a la función de distribución acumulativa (CDF) de los valores de píxeles en la vecindad.

Los píxeles cerca del límite de la imagen deben tratarse especialmente, porque su vecindario no estaría completamente dentro de la imagen. Esto se aplica, por ejemplo, a los píxeles a la izquierda o por encima del píxel azul en la figura. Esto se puede resolver extendiendo la imagen mediante la duplicación de líneas de píxeles y columnas con respecto al límite de la imagen. Simplemente copiar las líneas de píxeles en el borde no es apropiado, ya que conduciría a un histograma de vecindad con un pico alto.

Propiedades de AHE [ editar ]

• El tamaño de la región vecina es un parámetro del método. Constituye una escala de longitud característica: el contraste en escalas más pequeñas se mejora, mientras que el contraste en escalas más grandes se reduce.
• Debido a la naturaleza de la ecualización del histograma, el valor del resultado de un píxel bajo AHE es proporcional a su rango entre los píxeles de su vecindario. Esto permite una implementación eficiente en hardware especializado que puede comparar el píxel central con todos los demás píxeles del vecindario. ^[3]Se puede calcular un valor de resultado no normalizado sumando 2 por cada píxel con un valor más pequeño que el píxel central, y agregando 1 por cada píxel con el mismo valor.
• Cuando la región de la imagen que contiene la vecindad de un píxel es bastante homogénea con respecto a las intensidades, su histograma tendrá un pico intenso y la función de transformación asignará un rango estrecho de valores de píxel a todo el rango de la imagen resultante. Esto hace que AHE amplifique demasiado pequeñas cantidades de ruido en regiones de la imagen en gran parte homogéneas. ^[4]

Contraste Limited AHE [ editar ]

El AHE ordinario tiende a amplificar en exceso el contraste en regiones casi constantes de la imagen, ya que el histograma en tales regiones está altamente concentrado. Como resultado, AHE puede hacer que el ruido se amplifique en regiones cercanas a la constante. El contraste limitado AHE (CLAHE) es una variante de la ecualización adaptativa del histograma en la cual la amplificación del contraste es limitada, a fin de reducir este problema de la amplificación del ruido. ^[3]

En CLAHE, la amplificación de contraste en la vecindad de un valor de píxel dado viene dada por la pendiente de la función de transformación. Esto es proporcional a la pendiente de la función de distribución acumulativa devecindad (FDC) y, por lo tanto, al valor del histograma en ese valor de píxel. CLAHE limita la amplificación al recortar el histograma a un valor predefinido antes de calcular el CDF. Esto limita la pendiente de la CDF y por lo tanto de la función de transformación. El valor en el que se recorta el histograma, el llamado límite de clip, depende de la normalización del histograma y, por lo tanto, del tamaño de la región vecina. Los valores comunes limitan la amplificación resultante entre 3 y 4.

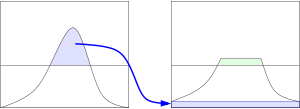
Es ventajoso no descartar la parte del histograma que excede el límite del clip, sino redistribuirlo por igual entre todos los contenedores de histogramas. ^[3]

La redistribución volverá a empujar algunas bandejas por encima del límite del clip (región sombreada en verde en la figura), dando como resultado un límite efectivo del clip que es mayor que el límite prescrito y cuyo valor exacto depende de la imagen. Si esto no es deseable, el procedimiento de redistribución se puede repetir recursivamente hasta que el exceso sea despreciable.

Cálculo eficiente por interpolación [ editar ]

La ecualización adaptativa del histograma en su forma directa presentada anteriormente, con y sin limitación de contraste, requiere el cálculo de un histograma de vecindario diferente y una función de transformación para cada píxel en la imagen. Esto hace que el método sea muy costoso computacionalmente.

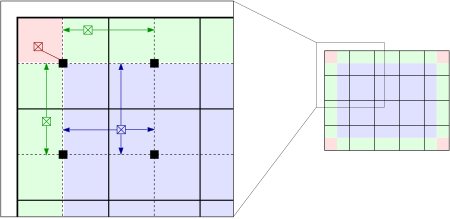
La interpolación permite una mejora significativa en la eficiencia sin comprometer la calidad del resultado. ^[3] La imagen se divide en mosaicos rectangulares del mismo tamaño, como se muestra en la parte derecha de la figura a continuación. (64 baldosas en 8 columnas y 8 filas son una opción común. ^[4] ) Se calcula una función de histograma, CDF y transformación para cada una de las fichas. Las funciones de transformación son apropiadas para los píxeles centrales del mosaico, cuadrados negros en la parte izquierda de la figura. Todos los demás píxeles se transforman con hasta cuatro funciones de transformación de los mosaicos con los píxeles centrales más cercanos a ellos, y se asignan valores interpolados. Los píxeles en la mayor parte de la imagen (azul sombreado) se interpolan bilinealmenteLos píxeles cercanos al límite (verde sombreado) se interpolan linealmente y los píxeles cercanos a las esquinas (rojo sombreado) se transforman con la función de transformación del mosaico de esquina. Los coeficientes de interpolación reflejan la ubicación de los píxeles entre los píxeles del centro del mosaico más cercano, de modo que el resultado es continuo a medida que el píxel se acerca al centro del mosaico.

Este procedimiento reduce el número de funciones de transformación que se van a computar dramáticamente y solo impone el pequeño costo adicional de la interpolación lineal.

Cálculo eficiente por actualización incremental de histograma [ editar ]

Una alternativa a colocar en mosaico la imagen es "deslizar" el rectángulo un píxel a la vez, y solo actualizar de manera incremental el histograma de cada píxel, ^[5] agregando la nueva fila de píxeles y restando la fila que queda atrás. Los autores originales denotan el algoritmo SWAHE (Ecualización del histograma adaptativo de ventana deslizante). La complejidad computacional del cálculo del histograma se reduce de O ( N² ) a O ( N ) (con N = ancho de píxel del rectángulo circundante); y como no hay mosaico, no se requiere un paso de interpolación final.

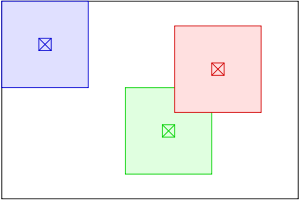
Alfa a la cobertura es una técnica de gráficos computarizados de muestreo múltiple , que utiliza el canal alfa de las texturas como máscara de cobertura para el suavizado . Esta técnica en particular es útil para situaciones en las que el follaje denso o el césped se deben representar en un videojuego . ^[1]

El muestreo múltiple alfa a cobertura se basa en el muestreo múltiple regular, excepto que la máscara de cobertura alfa se ANDA con la máscara multimuestra. Alfa a cobertura convierte la salida del componente alfa del sombreador de píxeles a una máscara de cobertura. Cuando se aplica el multisampling, cada fragmento de salida obtiene una transparencia de 0 o 1 según la cobertura alfa y el resultado del multisampling .

 el procesamiento de imágenes analógicas es cualquier tarea de procesamiento de imágenes que se realiza en señales analógicas bidimensionales por medios analógicos (a diferencia del procesamiento de imágenes digitales ). Básicamente, cualquier dato se puede representar en dos tipos nombrados como 1. Analógico 2.Digital si la representación gráfica de los datos se representa en formatos de ondas analógicas que se pueden denominar como imagen analógica. Por ejemplo: transmisión de televisión en días anteriores ... a través de los sistemas de antena parabólica ... donde la representación digital o el almacenamiento de datos en formato digital se denomina procesamiento de imagen digital, por ejemplo, datos de imagen almacenados en puertas lógicas digitales.

la difusión anisotrópica , también llamada difusión Perona-Malik , es una técnica que apunta a reducir el ruido de la imagen sin eliminar partes significativas del contenido de la imagen, generalmente bordes, líneas u otros detalles que son importantes para la interpretación de la imagen. . ^{[1] [2] [3] La} difusión anisotrópica se parece al proceso que crea un espacio de escala , donde una imagen genera una familia parametrizada de imágenes cada vez más borrosas basadas en un proceso de difusión . Cada una de las imágenes resultantes en esta familia se dan como una convolución.entre la imagen y un filtro Gaussiano isotrópico 2D , donde el ancho del filtro aumenta con el parámetro. Este proceso de difusión es una transformación lineal e invariante del espacio de la imagen original. La difusión anisotrópica es una generalización de este proceso de difusión: produce una familia de imágenes parametrizadas, pero cada imagen resultante es una combinación entre la imagen original y un filtro que depende del contenido local de la imagen original. Como consecuencia, la difusión anisotrópica es una transformación no lineal y variante del espacio de la imagen original.

En su formulación original, presentada por Perona y Malik en 1987, ^[1] el filtro variante de espacio es en realidad isótropo pero depende del contenido de la imagen de manera que se aproxime a una función de impulso cercana a los bordes y otras estructuras que deben conservarse en el Imagen sobre los diferentes niveles del espacio de escala resultante . Perona y Malik se refirieron a esta formulación como difusión anisotrópica , aunque el filtro adaptado localmente es isotrópico, pero también se ha denominado difusión no homogénea y no lineal ^[4] o difusión Perona-Malik ^[5]por otros autores. Una formulación más general permite que el filtro adaptado localmente sea realmente anisotrópico cerca de estructuras lineales como bordes o líneas: tiene una orientación dada por la estructura de manera que se alarga a lo largo de la estructura y se estrecha. Tales métodos se conocen como suavizado adaptado a la forma ^[6] [7] o difusión que mejora la coherencia . ^[8] Como consecuencia, las imágenes resultantes conservan estructuras lineales mientras que al mismo tiempo se realiza un suavizado a lo largo de estas estructuras. Ambos casos se pueden describir mediante una generalización de la ecuación de difusiónhabitual , donde el coeficiente de difusión, en lugar de ser un escalar constante, es una función de la posición de la imagen y asume una matriz.(o tensor ) valor (ver tensor de estructura ).

Si bien la familia de imágenes resultante puede describirse como una combinación entre la imagen original y los filtros de variante de espacio, el filtro adaptado localmente y su combinación con la imagen no tienen que realizarse en la práctica. La difusión anisotrópica normalmente se implementa por medio de una aproximación de la ecuación de difusión generalizada: cada nueva imagen en la familia se calcula aplicando esta ecuación a la imagen anterior. Por consiguiente, la difusión anisotrópica es un proceso iterativo en el que se utiliza un conjunto de cómputo relativamente simple para calcular cada imagen sucesiva en la familia y este proceso continúa hasta que se obtiene un grado suficiente de suavizado.

Definición formal [ editar ]

Formalmente dejemos $${\ displaystyle \ Omega \ subset \ mathbb {R} ^ {2}} denota un subconjunto del plano y $${\ displaystyle I (\ cdot, t): \ Omega \ rightarrow \ mathbb {R}} Al ser una familia de imágenes en escala de grises, la difusión anisotrópica se define como

$${\ displaystyle {\ frac {\ parcial I} {\ parcial t}} = \ mathrm {div} \ left (c (x, y, t) \ nabla I \ right) = \ nabla c \ cdot \ nabla I + c (x, y, t) \ Delta I}

dónde $${\ displaystyle \ Delta}denota el laplaciano ,$${\ displaystyle \ nabla}denota el gradiente ,$${\ displaystyle \ mathrm {div} (\ puntos)}es el operador de divergencia y$${\ displaystyle c (x, y, t)} Es el coeficiente de difusión. $${\ displaystyle c (x, y, t)}controla la velocidad de difusión y normalmente se elige como una función del degradado de la imagen para preservar los bordes de la imagen. Pietro Perona y Jitendra Malik fueron pioneros en la idea de la difusión anisotrópica en 1990 y propusieron dos funciones para el coeficiente de difusión:

$${\ displaystyle c \ left (\ | \ nabla I \ | \ right) = e ^ {- \ left (\ | \ nabla I \ | / K \ right) ^ {2}}}

y

$${\ displaystyle c \ left (\ | \ nabla I \ | \ right) = {\ frac {1} {1+ \ left ({\ frac {\ | \ nabla I \ |} {K}} \ right) ^ {2}}}}

La constante K controla la sensibilidad a los bordes y generalmente se elige experimentalmente o como una función del ruido en la imagen.

Motivación [ editar ]

Dejar $${\ displaystyle M}denota la variedad de imágenes suaves, luego las ecuaciones de difusión presentadas anteriormente se pueden interpretar como las ecuaciones de pendiente de gradiente para la minimización de la energía funcional$${\ displaystyle E: M \ rightarrow \ mathbb {R}} definido por

$${\ displaystyle E [I] = {\ frac {1} {2}} \ int _ {\ Omega} g \ left (\ | \ nabla I (x) \ | ^ {2} \ right) \, dx}

dónde $${\ displaystyle g: \ mathbb {R} \ rightarrow \ mathbb {R}}Es una función de valor real que veremos que está íntimamente relacionada con el coeficiente de difusión. Luego, para cualquier función de prueba infinitamente diferenciable y con soporte compacto$${\ displaystyle h}, tenemos

{\ displaystyle {\ begin {alineado} \ left. {\ frac {d} {dt}} \ right | _ {t = 0} E [I + ésimo] & = {\ frac {d} {dt}} { \ big |} _ {t = 0} {\ frac {1} {2}} \ int _ {\ Omega} g \ left (\ | \ nabla (I + th) (x) \ | ^ {2} \ derecha) \, dx \\ & = \ int _ {\ Omega} g '\ left (\ | \ nabla I (x) \ | ^ {2} \ right) \ nabla I \ cdot \ nabla h \, dx \ \ & = - \ int _ {\ Omega} \ mathrm {div} (g '\ left (\ | \ nabla I (x) \ | ^ {2} \ right) \ nabla I) h \, dx \ end { alineado}}}

donde la última línea sigue desde la integración multidimensional por partes. Dejando$${\ displaystyle \ nabla E_ {I}} denota el gradiente de E con respecto a la $${\ displaystyle L ^ {2} (\ Omega, \ mathbb {R})} Producto interno evaluado en I, esto da

$${\ displaystyle \ nabla E_ {I} = - \ mathrm {div} (g '\ left (\ | \ nabla I (x) \ | ^ {2} \ right) \ nabla I)}

Por lo tanto, las ecuaciones de pendiente de gradiente en la E funcional están dadas por

$${\ displaystyle {\ frac {\ parcial I} {\ parcial t}} = - \ nabla E_ {I} = \ mathrm {div} (g '\ left (\ | \ nabla I (x) \ | ^ {2 } \ derecha) \ nabla I)}

Así, dejando $${\ displaystyle c = g '} Obtenemos las ecuaciones de difusión anisotrópica.

Problema de la mala posedness [ editar ]

Coeficiente de difusión, $${\ displaystyle c (x, y, t)}, que es propuesto por Perona y Malik puede ser un valor negativo cuando {\ displaystyle \ parallel \ nabla I \ parallel ^ {2}> K ^ {2}}. Desde aquí, el sistema está restringido por una dimensión por simplicidad. Definamos la función de flujo como$${\ displaystyle \ Phi (s): = g (| s | ^ {2}) s}, dónde $${\ displaystyle s = \ nabla I (x, t)}y $${\ displaystyle g (| s | ^ {2}) = {1 \ sobre 1 + s ^ {2} / K ^ {2}}}.

La ecuación de Perona-Malik se puede reescribir en función de la función de flujo mediante

$${\ displaystyle \ parcial _ {t} I = \ nabla \ cdot \ Phi (s) = \ parcial _ {x} (\ Phi (\ parcial _ {x} I)) = \ Phi '(\ parcial _ {x } I) \ parcial _ {xx} I}. Aquí,$${\ displaystyle \ parcial _ {t}, \ parcial _ {x}, \ parcial _ {xx}}se denotan por primera derivada de tiempo, posición y segunda derivada de posición, respectivamente.

Ahora, está claro que $${\ displaystyle \ Phi '(\ partial _ {x} I)}juega un papel en el coeficiente de difusión de la ecuación de calor lineal. Calculando$${\ displaystyle \ Phi '(\ partial _ {x} I)},

$${\ displaystyle \ Phi '(\ partial _ {x} I) = {\ partial \ over \ partial s} {\ biggl (} {s \ over 1 + s ^ {2} / K ^ {2}} {\ biggr)} = {1-s ^ {2} / K ^ {2} \ sobre 1 + s ^ {2} / K ^ {2}}}.

Si {\ displaystyle 1-s ^ {2} / K ^ {2} <0 font="">El coeficiente de difusión se vuelve negativo y conduce a una difusión hacia atrás que mejora los contrastes de intensidad de la imagen en lugar de suavizarlos en el procesamiento de la imagen.

En términos de perspectiva teórica, la difusión hacia atrás no solo es físicamente antinatural, sino que también proporciona soluciones numéricamente inestables que son muy sensibles al parámetro ($${\ displaystyle K}). Además, se sabe que la difusión hacia atrás tiene numerosas soluciones y esto se denomina problema de mala posición.

Para evitar el problema, la regularización es necesaria y las personas han demostrado que las regularizaciones espaciales conducen a una solución de estado estacionario convergente y constante. ^[9]

Regularización [ editar ]

El modelo Perona-Malik modificado ^[10] (que también se conoce como regularización de la ecuación de PM) se tratará en esta sección. En este enfoque, lo desconocido está convuelto con un gaussiano dentro de la no linealidad para obtener la ecuación de Perona-Malik modificada.

$${\ displaystyle {\ frac {\ partial I} {\ partial t}} = \ mathrm {div} \ left (c (| DG _ {\ sigma} * I |) \ nabla I \ right)}

Dónde $${\ displaystyle G _ {\ sigma} = C {\ sigma} ^ {- \ left (1/2 \ right)} \ exp \ left (- | x | ^ {2} / 4 {\ sigma} \ right)}.

La buena posición de la ecuación se puede lograr mediante la regularización, pero también introduce un efecto de desenfoque, que es el principal inconveniente de la regularización. Se requiere un conocimiento previo del nivel de ruido ya que la elección del parámetro de regularización depende de ello.

Aplicaciones [ editar ]

La difusión anisotrópica se puede utilizar para eliminar el ruido de las imágenes digitales sin difuminar los bordes. Con un coeficiente de difusión constante, las ecuaciones de difusión anisotrópica se reducen a la ecuación de calor que es equivalente al desenfoque gaussiano. Esto es ideal para eliminar el ruido pero también difumina los bordes de manera indiscriminada. Cuando el coeficiente de difusión se elige como una función de búsqueda de borde, como en Perona-Malik, las ecuaciones resultantes fomentan la difusión (por lo tanto, el suavizado) dentro de las regiones y lo prohíben a través de bordes fuertes. Por lo tanto, los bordes se pueden conservar al eliminar el ruido de la imagen.

En la misma línea que la eliminación de ruido, la difusión anisotrópica se puede utilizar en los algoritmos de detección de bordes. Al ejecutar la difusión con un coeficiente de difusión de búsqueda de bordes para un cierto número de iteraciones, la imagen puede evolucionar hacia una imagen constante por partes, con los límites entre los componentes constantes que se detectan como bordes.