OCEANOGRAFÍA FÍSICA

FUERZA DE CORIOLIS - CONTINUACIÓN

Cañón en la plataforma giratoria [ editar ]

Esta sección puede ser demasiado técnica para que la mayoría de los lectores entiendan . Ayude a mejorarlo para que sea comprensible para los no expertos , sin eliminar los detalles técnicos. ( Junio ​​de 2010 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

Ver también: Fuerza ficticia § Cruzar un carrusel.

Cañón en el centro de un plato giratorio giratorio. Para golpear el objetivo ubicado en la posición 1 en el perímetro en el tiempo t = 0 s, el cañón debe apuntar por delante del objetivo en el ángulo θ. De esa manera, cuando la bala de cañón alcance la posición 3 en la periferia, el objetivo también estará en esa posición. En un marco de referencia inercial, la bala de cañón recorre una trayectoria radial recta hacia el objetivo (curva y _A ). Sin embargo, en el marco del plato giratorio, la trayectoria está arqueada (curva y _B ), como también se muestra en la figura.

Trayectoria exitosa de la bala de cañón vista desde la plataforma giratoria para tres ángulos de lanzamiento θ. Los puntos trazados son para los mismos pasos espaciados equitativamente en cada curva. La velocidad de bala de cañón v se mantiene constante y la velocidad de rotación angular ω se varía para lograr un "golpe" exitoso para θ seleccionado. Por ejemplo, para un radio de 1 my una velocidad de bala de cañón de 1 m / s, el tiempo de vuelo t _f = 1 s, y ωt _f = θ → ω y θ tienen el mismo valor numérico si θSe expresa en radianes. El espaciado más amplio de los puntos trazados a medida que se aproxima al objetivo muestra que la velocidad de la bala de cañón se está acelerando como se ve en la plataforma giratoria, debido a las fuerzas ficticias de Coriolis y centrífugas.

Componentes de aceleración en un momento anterior (arriba) y en el momento de llegada al objetivo (abajo)

La aceleración de Coriolis, la aceleración centrífuga y los vectores de aceleración neta en tres puntos seleccionados de la trayectoria como se ve en el plato giratorio.

La animación en la parte superior de este artículo es una ilustración clásica de la fuerza de Coriolis. Otra visualización de Coriolis y fuerzas centrífugas es este clip de animación.

Dado el radio R del plato giratorio en esa animación, la velocidad de rotación angular ω y la velocidad de la bala de cañón (supuesta constante) v , el ángulo correcto θ para apuntar y golpear el objetivo en el borde del plato giratorio puede ser calculado.

El marco de referencia inercial proporciona una manera de manejar la pregunta: calcular el tiempo de interceptación, que es t _f = R / v . Luego, el plato giratorio gira en un ángulo ω t _f en este tiempo. Si el cañón está apuntando con un ángulo θ = ω t _f = ω R / v , entonces la bala de cañón llega a la periferia en la posición número 3 al mismo tiempo que el objetivo.

Ninguna discusión sobre la fuerza de Coriolis puede llegar a esta solución tan sencillamente, por lo que la razón para tratar este problema es demostrar el formalismo de Coriolis en una situación fácilmente visualizable.

Trayectoria en el marco inercial [ editar ]

La trayectoria en el marco inercial (denotado A ) es una trayectoria radial de línea recta en el ángulo θ. La posición del cañón en coordenadas ( x , y ) en el tiempo t es:

$${\ displaystyle \ mathbf {r} _ {A} (t) = vt \ \ left (\ cos \ theta, \ \ sin \ theta \ right) \.}

En el marco de la plataforma giratoria (indicado como B ), los ejes x - y giran a una velocidad angular ω, por lo que la trayectoria se convierte en:

$${\ displaystyle \ mathbf {r} _ {B} (t) = vt \ \ left (\ cos (\ theta - \ omega t), \ \ sin (\ theta - \ omega t) \ right) \,}

y tres ejemplos de este resultado se representan en la figura.

Aceleraciones [ editar ]

Componentes de la aceleración [ editar ]

Para determinar los componentes de la aceleración, se usa una expresión general del artículo fuerza ficticia :

$${\ displaystyle \ mathbf {a} _ {B} = \ mathbf {a} _ {A} \; - \; 2 {\ boldsymbol {\ Omega}} \ times \ mathbf {v} _ {B} \; \; {\ boldsymbol {\ Omega}} \ times \ left ({\ boldsymbol {\ Omega}} \ times \ mathbf {r} _ {B} \ right) \; - \; {\ frac {d {\ boldsymbol {\ Omega}}} {dt}} \ times \ mathbf {r} _ {B}}

en el que el término en Ω × v _B es la aceleración de Coriolis y el término en Ω × ( Ω × r _B ) es la aceleración centrífuga. Los resultados son (sea α = θ - ω t ):

{\ displaystyle {\ begin {alineado} {\ boldsymbol {\ Omega}} \ times \ mathbf {r} _ {B} & = \; {\ begin {vmatrix} {\ boldsymbol {i}} & {\ boldsymbol { j}} & {\ boldsymbol {k}} \\ 0 & 0 & \ omega \\ tv \ cos \ alpha & tv \ sin \ alpha & 0 \ end {vmatrix}} \; = \ omega t \, v \ left (- \ sin \ alpha, \ cos \ alpha \ right) \, \\ {\ boldsymbol {\ Omega}} \ times \ left ({\ boldsymbol {\ Omega}} \ times \ mathbf {r} _ {B} \ right) & = \; {\ begin {vmatrix} {\ boldsymbol {i}} & {\ boldsymbol {j}} & {\ boldsymbol {k}} \\ 0 & 0 & \ omega \\ - \ omega tv \ sin \ alpha & \ omega tv \ cos \ alpha & 0 \ end {vmatrix}} \; = \ omega ^ {2} t \, v \ left (- \ cos \ alpha, - \ sin \ alpha \ right), \ end {alineado}}}

Produciendo aceleraciones [ editar ]

Produciendo una aceleración centrífuga:

$${\ displaystyle \ mathbf {a} _ {\ text {Cfgl}} = \ omega ^ {2} vt \ left (\ cos \ alpha, \ \ sin \ alpha \ right) = \ omega ^ {2} \ mathbf { r} _ {B} (t) \.}

También:

{\ displaystyle {\ begin {alineado} \ mathbf {v} _ {B} = {\ frac {d \ mathbf {r} _ {B} (t)} {dt}} & = (v \ cos \ alpha + \ omega tv \ sin \ alpha, \ v \ sin \ alpha - \ omega tv \ cos \ alpha, \ 0) \, \\ {\ boldsymbol {\ Omega}} \ times \ mathbf {v} _ {B} & = {\ begin {vmatrix} {\ boldsymbol {i}} & {\ boldsymbol {j}} & {\ boldsymbol {k}} \\ 0 & 0 & \ omega \\ v \ cos \ alpha + {} & v \ sin \ alpha - {} & \\\ quad \ omega tv \ sin \ alpha & \ quad \ omega tv \ cos \ alpha & 0 \ end {vmatrix}} \, \ end {alineado}}}

produciendo una aceleración de Coriolis:

{\ displaystyle {\ begin {alineado} \ mathbf {a} _ {\ text {Cor}} & = - 2 \ left [- \ omega v \ left (\ sin \ alpha - \ omega t \ cos \ alpha \ right ), \ \ omega v \ left (\ cos \ alpha + \ omega t \ sin \ alpha \ right) \ right] \\ & = 2 \ omega v \ left (\ sin \ alpha, \ - \ cos \ alpha \ derecha) -2 \ omega ^ {2} \ mathbf {r} _ {B} (t) \. \ end {alineado}}}

Estas aceleraciones se muestran en los diagramas para un ejemplo particular.

Se ve que la aceleración de Coriolis no solo cancela la aceleración centrífuga, sino que juntas proporcionan una red "centrípeta", componente radialmente hacia adentro de la aceleración (es decir, dirigida hacia el centro de rotación): ^[33]

$${\ displaystyle \ mathbf {a _ {\ mathrm {Cptl}}} = - \ omega ^ {2} \ mathbf {r_ {B}} (t) \,}

y un componente adicional de aceleración perpendicular a r _B ( t ):

$${\ displaystyle \ mathbf {a} _ {C \ perp} = 2 \ omega v \ left (\ sin \ alpha, \ - \ cos \ alpha \ right) \.}

El componente "centrípeto" de la aceleración se parece al movimiento circular en el radio r _B , mientras que el componente perpendicular es dependiente de la velocidad, aumentando con la velocidad radial v y dirigido a la derecha de la velocidad. La situación podría describirse como un movimiento circular combinado con una "aceleración aparente de Coriolis" de 2ω v . Sin embargo, este es un etiquetado aproximado: una designación cuidadosa de la verdadera fuerza centrípeta se refiere a un marco de referencia local que emplea las direcciones normal y tangencial a la trayectoria, no coordenadas referidas al eje de rotación.

Estos resultados también se pueden obtener directamente por dos diferenciaciones de tiempo de r _B ( t ). El acuerdo de los dos enfoques demuestra que uno podría comenzar desde la expresión general para la aceleración ficticia anterior y derivar las trayectorias que se muestran aquí. Sin embargo, trabajar desde la aceleración hasta la trayectoria es más complicado que el procedimiento inverso utilizado aquí, que es posible en este ejemplo al conocer la respuesta de antemano.

Como resultado de este análisis, aparece un punto importante: todas las aceleraciones ficticias deben incluirse para obtener la trayectoria correcta. En particular, además de la aceleración de Coriolis, la fuerza centrífugajuega un papel esencial. Es fácil obtener la impresión de las discusiones verbales sobre el problema de la bala de cañón, que se centran en mostrar el efecto de Coriolis en particular, que la fuerza de Coriolis es el único factor que debe considerarse, ^[34] pero no es así. ^[35] Un plato giratorio para el cual la fuerza de Coriolis es el único factor es el plato giratorio parabólico. Una situación algo más compleja es el ejemplo idealizado de rutas de vuelo en largas distancias, donde la fuerza centrífuga de la trayectoria y la sustentación aeronáutica se contrarrestan por la atracción gravitacional . ^[36] [37]

Bola lanzada en un carrusel giratorio [ editar ]

Un carrusel está girando a la izquierda. Panel izquierdo : una bola es lanzada por un lanzador a las 12:00 en punto y viaja en línea recta hacia el centro del carrusel. Mientras viaja, el lanzador gira en sentido contrario a las agujas del reloj. Panel derecho: el movimiento de la bola visto por el lanzador, que ahora permanece a las 12:00 en punto, porque no hay rotación desde su punto de vista.

La figura ilustra una bola lanzada desde las 12:00 en punto hacia el centro de un carrusel giratorio a la izquierda. A la izquierda, la pelota es vista por un observador estacionario sobre el carrusel, y la bola viaja en línea recta hacia el centro, mientras que el lanzador de bolas gira en sentido contrario a las agujas del reloj con el carrusel. A la derecha, la bola es vista por un observador que gira con el carrusel, por lo que el lanzador de bolas parece quedarse a las 12:00 en punto. La figura muestra cómo se puede construir la trayectoria de la bola vista por el observador en rotación.

A la izquierda, dos flechas ubican la bola en relación con el lanzador de bolas. Una de estas flechas es desde el lanzador hasta el centro del carrusel (que proporciona la línea de visión del lanzador de la pelota), y la otra parte desde el centro del carrusel hasta la pelota. (Esta flecha se acorta cuando la bola se acerca al centro). Una versión desplazada de las dos flechas se muestra punteada.

A la derecha se muestra este mismo par de flechas de puntos, pero ahora el par está girado rígidamente, de modo que la flecha correspondiente a la línea de visión del lanzador de bolas hacia el centro del carrusel se alinea con las 12:00 en punto. La otra flecha del par ubica la bola en relación con el centro del carrusel, proporcionando la posición de la bola como la ve el observador que gira. Siguiendo este procedimiento para varias posiciones, la trayectoria en el marco de referencia giratorio se establece como se muestra en la trayectoria curva en el panel de la derecha.

La bola viaja en el aire, y no hay fuerza neta sobre ella. Para el observador estacionario, la pelota sigue una trayectoria en línea recta, por lo que no hay problema en cuadrar esta trayectoria con una fuerza neta cero. Sin embargo, el observador rotativo ve un camino curvo . La cinemática insiste en que debe existir una fuerza (empujando a la derecha de la dirección de desplazamiento instantánea para girar en sentido contrario a las agujas del reloj ) para causar esta curvatura, por lo que el observador giratorio está obligado a invocar una combinación de fuerzas centrífugas y de Coriolis para proporcionar la red. Fuerza necesaria para provocar la trayectoria curva.

Pelota que rebota [ editar ]

Vista de pájaro del carrusel. El carrusel gira en sentido horario. Se ilustran dos puntos de vista: el de la cámara en el centro de rotación que gira con el carrusel (panel izquierdo) y el del observador inercial (estacionario) (panel derecho). Ambos observadores acuerdan en un momento dado qué tan lejos está la pelota del centro del carrusel, pero no en su orientación. Los intervalos de tiempo son 1/10 de tiempo desde el lanzamiento hasta el rebote.

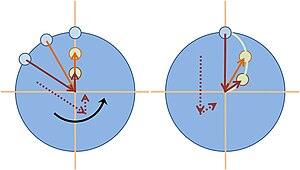
La figura describe una situación más compleja en la que la bola lanzada en un plato giratorio rebota en el borde del carrusel y luego regresa a la lanzadora, que atrapa la bola. El efecto de la fuerza de Coriolis en su trayectoria se muestra de nuevo como lo ven dos observadores: un observador (denominado "cámara") que gira con el carrusel y un observador inercial. La figura muestra una vista de pájaro basada en la misma velocidad de la bola en las rutas de avance y retorno. Dentro de cada círculo, los puntos trazados muestran los mismos puntos de tiempo. En el panel izquierdo, desde el punto de vista de la cámara en el centro de rotación, el lanzador (cara sonriente) y el riel están en ubicaciones fijas, y la bola hace un arco muy considerable en su viaje hacia el riel, y toma una dirección más directa. Ruta en el camino de vuelta. Desde el punto de vista del lanzador de bolas,

En el carrusel, en lugar de lanzar la bola directamente a una barra para rebotar, el lanzador debe lanzar la bola hacia la derecha del objetivo y la bola luego parece a la cámara que se incline continuamente hacia la izquierda de su dirección de viaje para golpear el riel ( izquierda porque el carrusel está girando hacia la derecha)). La bola parece inclinarse hacia la izquierda desde la dirección de desplazamiento tanto hacia adentro como hacia atrás en las trayectorias. La trayectoria curva requiere que este observador reconozca una fuerza neta hacia la izquierda en la bola. (Esta fuerza es "ficticia" porque desaparece para un observador estacionario, como se explica brevemente). Para algunos ángulos de lanzamiento, una trayectoria tiene partes donde la trayectoria es aproximadamente radial, y la fuerza de Coriolis es la principal responsable de la aparente desviación del bola (la fuerza centrífuga es radial desde el centro de rotación y causa poca desviación en estos segmentos). Sin embargo, cuando una trayectoria se aleja de la radial, la fuerza centrífuga contribuye significativamente a la desviación.

La trayectoria de la bola a través del aire es recta cuando la observan observadores que se encuentran en el suelo (panel derecho). En el panel de la derecha (observador estacionario), el lanzador de bolas (cara sonriente) está a las 12 en punto y el riel desde el que rebota la bola está en la posición uno (1). Desde el punto de vista del espectador inercial, las posiciones uno (1), dos (2), tres (3) están ocupadas en secuencia. En la posición 2, la pelota golpea el riel, y en la posición 3 la pelota regresa al tirador. Se siguen caminos en línea recta porque la bola está en vuelo libre, por lo que este observador requiere que no se aplique fuerza neta.