OCEANOGRAFÍA FÍSICA

onda cnoidal es una solución de onda periódica no lineal y exacta de la ecuación de Korteweg – de Vries . Estas soluciones están en términos de la función elíptica de Jacobi cn , es por eso que se acuñan cn olas oidal. Se utilizan para describir ondas de gravedad de superficie de longitud de onda bastante larga , en comparación con la profundidad del agua.

Las soluciones de ondas cnoidales fueron derivadas por Korteweg y de Vries , en su artículo de 1895 en el que también proponen su ecuación de onda larga dispersiva , ahora conocida como la ecuación de Korteweg-de Vries. En el límite de la longitud de onda infinita , la onda cnoidal se convierte en una onda solitaria .

La ecuación de Benjamin – Bona – Mahony ha mejorado el comportamiento de onda corta , en comparación con la ecuación de Korteweg – de Vries, y es otra ecuación de onda unidireccional con soluciones de onda cnoidal. Además, dado que la ecuación de Korteweg – de Vries es una aproximación a las ecuaciones de Boussinesqpara el caso de la propagación de ondas unidireccionales, las ondas cnoidales son soluciones aproximadas a las ecuaciones de Boussinesq.

Las soluciones de ondas cnoidales pueden aparecer en otras aplicaciones además de las ondas de gravedad de superficie, por ejemplo, para describir las ondas acústicas de iones en la física de plasma .

Bombarderos del Ejército de los EE. UU. Vuelan sobre oleaje casi periódico en aguas poco profundas, cerca de la costa de Panamá (1933). Las crestas afiladas y los canales muy planos son característicos de las ondas cnoidales.

Una onda cnoidal, caracterizada por crestas más agudas y canales más planos que en una onda sinusoidal . Para el caso mostrado, el parámetro elíptico es m  = 0.9.

Cruce de oleaje , formado por trenes de olas casi cnoidales. Foto tomada desde Phares des Baleines (Whale Lighthouse) en el punto occidental de Île de Ré (Isla de Rhé), Francia, en el Océano Atlántico .

Fondo [ editar ]

Ecuaciones de Korteweg – de Vries y Benjamin – Bona – Mahony [ editar ]

Validez de varias teorías para ondas de agua periódicas, según Le Méhauté (1976). ^[2] El área azul claro proporciona el rango de validez de la teoría de la onda cnoidal; amarillo claro para la teoría de las ondas aéreas ; y las líneas azules discontinuas demarcan entre el orden requerido en la teoría de la onda de Stokes . El sombreado gris claro proporciona la extensión del rango mediante aproximaciones numéricas utilizando la teoría de la función de la corriente de quinto orden , para ondas altas ( H  > ¼ H _rompimiento ).

La ecuación de Korteweg – de Vries ( ecuación de KdV) se puede usar para describir la propagación unidireccional de ondas no lineales y débilmente débiles, donde significa onda larga: tener longitudes de onda largas en comparación con la profundidad media del agua, de ondas de gravedad de superficie en un fluido capa. La ecuación de KdV es una ecuación de onda dispersiva , que incluye efectos de dispersión de frecuencia y dispersión de amplitud . En su uso clásico, la ecuación de KdV es aplicable para longitudes de onda λ en exceso de aproximadamente cinco veces la profundidad promedio del agua h , entonces para λ  > 5  h ; y para el período τ mayor que$${\ displaystyle \ scriptstyle 7 {\ sqrt {h / g}}}con g la fuerza de la aceleración gravitacional . ^[3] Para prever la posición de la ecuación de KdV dentro del alcance de las aproximaciones de onda clásicas, se distingue de las siguientes maneras:

• La ecuación de Korteweg – de Vries - describe la propagación hacia adelante de ondas débilmente no lineales y dispersivas, para ondas largas con λ  > 7  h .
• Las ecuaciones de aguas someras - también son no lineales y tienen dispersión de amplitud, pero no dispersión de frecuencia; son válidos para olas muy largas, λ  > 20  h .
• Ecuaciones de Boussinesq : tienen el mismo rango de validez que la ecuación de KdV (en su forma clásica), pero permiten la propagación de la onda en direcciones arbitrarias, por lo que no solo las ondas se propagan hacia adelante. El inconveniente es que las ecuaciones de Boussinesq son a menudo más difíciles de resolver que la ecuación de KdV; y en muchas aplicaciones, las reflexiones de onda son pequeñas y pueden descuidarse.
• Teoría de la onda aérea : tiene una dispersión de frecuencia total, tan válida para la profundidad y la longitud de onda arbitrarias, pero es una teoría lineal sin dispersión de amplitud, limitada a las ondas de baja amplitud.
• Teoría de la onda de Stokes : un enfoque de la serie de perturbaciones para la descripción de ondas débilmente no lineales y dispersivas, especialmente exitosas en aguas más profundas para longitudes de onda relativamente cortas, en comparación con la profundidad del agua. Sin embargo, para las ondas largas, el enfoque de Boussinesq, como también se aplica en la ecuación de KdV, a menudo se prefiere. Esto se debe a que, en aguas someras, la serie de perturbaciones de Stokes necesita muchos términos antes de la convergencia hacia la solución, debido a las crestas de picoy los largos canales planosde las ondas no lineales. Mientras que los modelos KdV o Boussinesq ofrecen buenas aproximaciones para estas ondas no lineales largas.

La ecuación de KdV se puede derivar de las ecuaciones de Boussinesq, pero se necesitan suposiciones adicionales para poder dividir la propagación de la onda hacia adelante. Para aplicaciones prácticas, la ecuación de Benjamin – Bona – Mahony ( ecuación de BBM) es preferible a la ecuación de KdV, un modelo de propagación hacia adelante similar a KdV pero con un comportamiento de dispersión de frecuencia mucho mejor en longitudes de onda más cortas. Se pueden obtener mejoras adicionales en el rendimiento de onda corta al comenzar a derivar una ecuación de onda unidireccional a partir de un modelo moderno mejorado de Boussinesq, válido para longitudes de onda incluso más cortas. ^[4]

Olas Cnoidal [ editar ]

Perfiles de ondas cnoidales para tres valores del parámetro melíptico .

azul	: m = 0,
rojo	: m = 0.9 y
negro	: m = 0.99999.

Las soluciones de ondas cnoidales de la ecuación de KdV fueron presentadas por Korteweg y de Vries en su artículo de 1895, cuyo artículo se basa en la tesis doctoral de De Vries en 1894. ^[5] Soluciones de ondas solitarias para ondas largas no lineales y dispersivas se habían encontrado anteriormente por Boussinesq en 1872, y Rayleigh en 1876. La búsqueda de estas soluciones fue provocada por las observaciones de esta ola solitaria (o "ola de traducción") por Russell , tanto en la naturaleza como en experimentos de laboratorio. ^[4] Las soluciones de ondas cnoidales de la ecuación de KdV son estables con respecto a pequeñas perturbaciones. ^[6]

La elevación de la superficie η ( x , t ), en función de la posición horizontal x y el tiempo t , para una onda cnoidal viene dada por: ^[7]

{\ displaystyle \ eta (x, t) = \ eta _ {2} + H \, \ operatorname {cn} ^ {2} \, \ left ({\ begin {array} {c | c} \ displaystyle 2 \ , K (m) \, {\ frac {xc \, t} {\ lambda}} & m \ end {array}} \ derecha),}

donde H es la altura de la onda , λ es la longitud de onda , c es la velocidad de la fase y η ₂ es la elevación del canal . Además, cn es una de las funciones elípticas de Jacobi y K ( m ) es la integral elíptica completa del primer tipo ; Ambos dependen del parámetro elíptico m . El último, m , determina la forma de la onda cnoidal. Para migual a cero, la onda cnoidal se convierte en coseno.función, mientras que para valores cercanos a uno, la onda cnoidal obtiene crestas y picos muy (muy) planos. Para valores de m menos de 0.95, la función cnoidal se puede aproximar con funciones trigonométricas. ^[8]

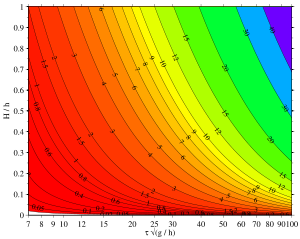
Un parámetro sin dimensiones importante para las ondas largas no lineales ( λ  ≫  h ) es el parámetro de Ursell :

$${\ displaystyle U = {\ frac {H \, \ lambda ^ {2}} {h ^ {3}}} = {\ frac {H} {h}} \, \ left ({\ frac {\ lambda} {h}} \ derecha) ^ {2}.}

Para valores pequeños de U , digamos U  <5 font="" nbsp="">^[9] se puede usar una teoría lineal, y en valores más altos se deben usar teorías no lineales, como la teoría de la onda cnoidal. La zona de demarcación entre —de tercer o quinto orden— las teorías de onda de Stokes y cnoidal está en el rango 10–25 del parámetro de Ursell. ^[10] Como puede verse en la fórmula para el parámetro Ursell, para una altura de onda relativa H / h dada, el parámetro Ursell, y por lo tanto también la no linealidad, crece rápidamente al aumentar la longitud de onda relativa λ / h .

Basado en el análisis del problema no lineal completo de las ondas de gravedad superficial dentro de la teoría del flujo potencial , las ondas cnoidales anteriores pueden considerarse el término de orden más bajo en una serie de perturbaciones. Las teorías de ondas cnoidales de orden superior siguen siendo válidas para ondas más cortas y más no lineales. Fenton desarrolló una teoría de la onda cnoidal de quinto orden en 1979. ^[11] En el artículo de revisión de Fenton se ofrece una descripción detallada y una comparación de las teorías de onda cnoidal de Stokes de quinto orden. ^[12]

Las descripciones de ondas cnoidales, a través de una renormalización, también son adecuadas para ondas en aguas profundas, incluso a una profundidad de agua infinita; según lo encontrado por Clamond. ^[13] [14] Una descripción de las interacciones de las ondas cnoidales en aguas poco profundas, tal como se encuentra en los mares reales, fue proporcionada por Osborne en 1994. ^[15]

Soluciones de onda periódica [ editar ]

Ecuación de Korteweg – de Vries [ editar ]

La ecuación de Korteweg – de Vries ( ecuación de KdV), como se usa para las ondas de agua y en forma dimensional, es: ^[16]

$${\ displaystyle \ parcial _ {t} \ eta + {\ sqrt {gh}} \; \ parcial _ {x} \ eta + {\ tfrac {3} {2}} \, {\ sqrt {\ frac {g } {h}}} \; \ eta \, \ partial _ {x} \ eta + {\ tfrac {1} {6}} \, h ^ {2} \, {\ sqrt {gh}} \; \ parcial _ {x} ^ {3} \ eta = 0,}

dónde

η	: elevación de la superficie , una función de x y t , con la dirección positiva hacia arriba (gravedad opuesta),
X	: coordenada horizontal,
t	: hora,
sol	: el valor de la gravedad de la Tierra ,
h	: la profundidad media del agua, y
∂ x y ∂t	: operadores de derivada parcial con respecto a x y t .

espectáculo

  Detalles de la derivación.

Aumento relativo de la velocidad de fase de las soluciones de ondas cnoidales para la ecuación de Korteweg – de Vries en función de 1− m , siendo m el parámetro elíptico. 
El eje horizontal está en una escala logarítmica , de 10 ⁻⁶ a 10 ⁰ = 1. 
La figura es para cantidades no dimensionales, es decir , la velocidad de fase c se hace adimensional con la velocidad de fase de aguas poco profundas$${\ displaystyle \ scriptstyle {\ sqrt {gh}}}, y la altura de la ola H se hace adimensional con la profundidad media del agua h .

La solución de onda cnoidal de la ecuación de KdV es: ^[7]

{\ displaystyle \ eta (x, t) = \ eta _ {2} + H \, \ operatorname {cn} ^ {2} \ left ({\ begin {array} {c | c} \ displaystyle {\ frac { xc \, t} {\ Delta}} & m \ end {array}} \ right),}

con H la altura de la ola: la diferencia entre la cresta y la elevación del canal , η ₂ la elevación del canal, m el parámetro elíptico, c la velocidad de la fase y cn una de las funciones elípticas de Jacobi . El nivel de canal η ₂ y el parámetro de ancho Δ se pueden expresar en términos de H, h y m : ^[7]

$${\ displaystyle \ eta _ {2} = {\ frac {H} {m}} \, \ left (1-m - {\ frac {E (m)} {K (m)}} \ right),   y   $${\ displaystyle \ Delta = {\ frac {\ lambda} {2 \, K (m)}} \, = h \, {\ sqrt {{\ frac {4} {3}} {\ frac {m \, S.S}}}},}

con K ( m ) la integral elíptica completa del primer tipo y E ( m ) la integral elíptica completa del segundo tipo . Tenga en cuenta que K ( m ) y E ( m ) se indican aquí como una función del parámetro elíptico my no como una función del módulo elíptico k , con m  =  k ² .

La longitud de onda λ , la velocidad de fase c y el período deonda τ están relacionados con H , h y m por: ^[7]

$${\ displaystyle \ lambda = h \, {\ sqrt {{\ frac {16} {3}} {\ frac {m \, h} {H}}}} \; K (m),}   $${\ displaystyle c = {\ sqrt {gh}} \, \ left [1 + {\ frac {H} {m \, h}} \, \ left (1 - {\ frac {1} {2}} \ , m - {\ frac {3} {2}} \, {\ frac {E (m)} {K (m)}} \ derecha) \ derecha]}   y   $${\ displaystyle \ tau = {\ frac {\ lambda} {c}},}

con g la gravedad de la tierra .

La mayoría de las veces, los parámetros de onda conocidos son la altura de onda H , la profundidad media del agua h , la aceleración gravitacional g , y la longitud de onda λ o bien el período τ . Luego, las relaciones anteriores para λ , c y τ se utilizan para encontrar el parámetro m elíptico . Esto requiere solución numérica por algún método iterativo . ^[3]

Ecuación de Benjamin – Bona – Mahony [ editar ]

La ecuación de Benjamin – Bona – Mahony ( ecuación de BBM), o ecuación de onda larga regularizada (RLW), está en forma dimensional dada por: ^[20]

$${\ displaystyle \ parcial _ {t} \ eta + {\ sqrt {g \, h}} \, \ parcial _ {x} \ eta + {\ tfrac {3} {2}} \, {\ sqrt {\ frac {g} {h}}} \, \ eta \, \ partial _ {x} \ eta - {\ tfrac {1} {6}} \, h ^ {2} \, \ partial _ {t} \ , \ parcial _ {x} ^ {2} \ eta = 0.}

Todas las cantidades tienen el mismo significado que para la ecuación de KdV. La ecuación de BBM a menudo se prefiere a la ecuación de KdV porque tiene un mejor comportamiento de onda corta. ^[20]

espectáculo

  Detalles de la derivación.

La solución de onda cnoidal de la ecuación de BBM, junto con las relaciones asociadas para los parámetros es: ^[21]

${\displaystyle {\begin{aligned}\eta (x,t)&=\eta _{2}+H\,\operatorname {cn} ^{2}\left({\begin{array}{c|c}\displaystyle {\frac {x-c\,t}{\Delta }}&m\end{array}}\right),\\\eta _{2}&={\frac {H}{m}}\,\left(1-m-{\frac {E(m)}{K(m)}}\right),\\\Delta &=h\,{\sqrt {{\frac {4}{3}}\,{\frac {m\,h}{H}}\,{\frac {c}{\sqrt {g\,h}}}}}&&={\frac {\lambda }{2\,K(m)}},\\\lambda &=h\,{\sqrt {{\frac {16}{3}}\,{\frac {m\,h}{H}}\,{\frac {c}{\sqrt {gh}}}}}\;K(m),\\c&={\sqrt {gh}}\,\left[1+{\frac {H}{m\,h}}\,\left(1-{\frac {1}{2}}\,m-{\frac {3}{2}}\,{\frac {E(m)}{K(m)}}\right)\right]&&{\text{and}}\\\tau &={\frac {\lambda }{c}}.\end{aligned}}}$

La única diferencia con la solución de onda cnoidal de la ecuación de KdV está en la ecuación para la longitud de onda λ . ^[21] Para aplicaciones prácticas, generalmente se proporciona la profundidad del agua h , la altura de la ola H , la aceleración gravitacional g , y la longitud de onda λ o, con mayor frecuencia, el período (física) τ . Luego, el parámetro elíptico m debe determinarse a partir de las relaciones anteriores para λ , c y τ a través de algún método iterativo . ^[3]

Ejemplo [ editar ]

Relaciones de parámetros para soluciones de onda cnoidal de la ecuación de Korteweg – de Vries. Se muestra −log ₁₀  (1− m ), con m el parámetro elíptico de las integrales elípticas completas , ^[19] en función del período adimensional τ  √ g / hy la alturarelativa de la onda H  /  h . Los valores a lo largo de las líneas de contorno son −log ₁₀  (1− m ), por lo que un valor 1 corresponde con m  = 1 - 10 ⁻¹  = 0.9 y un valor 40 con m  = 1 - 10 ⁻⁴⁰ .

En este ejemplo, se considera una onda cnoidal según la ecuación de Korteweg – de Vries (KdV). Se dan los siguientes parámetros de la onda:

• profundidad media del agua h = 5 m (16 pies),
• altura de la ola H = 3 m (9.8 pies),
• periodo de onda τ = 7 s , y
• aceleración gravitacional g = 9.81 m / s ² (32 pies / s ² ).

En lugar del período τ , en otros casos, la longitud de onda λpuede ocurrir como una cantidad conocida de antemano.

Primero, se calcula el período adimensional:

$${\ displaystyle \ tau \, {\ sqrt {\ frac {g} {h}}} = 9.80,}

que es más grande que siete, el tiempo suficiente para que la teoría cnoidal sea válida. El principal desconocido es el parámetro elíptico m . Esto debe determinarse de tal manera que el período de onda τ , como se calcula a partir de la teoría de la onda cnoidal para la ecuación de KdV:

$${\ displaystyle \ lambda = h \, {\ sqrt {{\ frac {16} {3}} {\ frac {m \, h} {H}}}} \; K (m),}   $${\ displaystyle c = {\ sqrt {gh}} \, \ left [1 + {\ frac {H} {m \, h}} \, \ left (1 - {\ frac {1} {2}} \ , m - {\ frac {3} {2}} \, {\ frac {E (m)} {K (m)}} \ derecha) \ derecha]}   y   $${\ displaystyle \ tau = {\ frac {\ lambda} {c}},}

es consistente con el valor dado de τ ; aquí λ es la longitud de onda yc es la velocidad de fase de la onda. Además, K ( m ) y E ( m ) son integrales elípticas completas del primer y segundo tipo, respectivamente. La búsqueda del parámetro elíptico m se puede realizar por prueba y error , o mediante el uso de un algoritmonumérico de búsqueda de raíces . En este caso, a partir de una suposición inicial m _init  = 0.99, por prueba y error la respuesta

$${\ displaystyle m = 0.9832 \,}

es encontrado. Dentro del proceso, la longitud de onda λ y la velocidad de fase c se han calculado:

• longitud de onda λ = 50.8 m (167 pies), y
• velocidad de fase c = 7.26 m / s (23.8 pies / s).

La velocidad de fase c puede compararse con su valor.$${\ displaystyle \ scriptstyle {\ sqrt {gh}}}De acuerdo con las ecuaciones de aguas poco profundas :

$${\ displaystyle {\ frac {c} {\ sqrt {g \, h}}} = 1.0376,}

mostrando un incremento del 3.8% debido al efecto de la dispersión de amplitud no lineal , que vence en este caso por la reducción de la velocidad de fase por dispersión de frecuencia .

Ahora que se conoce la longitud de onda, también se puede calcular el número de Ursell :

$${\ displaystyle U = {\ frac {H \, \ lambda ^ {2}} {h ^ {3}}} = 62,}

lo que no es pequeño, por lo que la teoría de la onda lineal no es aplicable, pero la teoría de la onda cnoidal sí lo es. Finalmente, la relación de longitud de onda a profundidad es λ  /  h  = 10.2> 7, lo que nuevamente indica que esta onda es lo suficientemente larga como para ser considerada como una onda cnoidal.

Límite de onda solitario [ editar ]

Para ondas no lineales muy largas, con el parámetro m cerca de uno, m  → 1, la función elíptica de Jacobi cn se puede aproximar en ^[22]

$${\ displaystyle \ operatorname {cn} \ left (z | m \ right) \ approx \ operatorname {sech} (z) - {\ tfrac {1} {4}} \, (1-m) \, {\ Bigl [} \ sinh (z) \; \ cosh (z) -z {\ Bigr]} \, \ tanh (z) \; \ operatorname {sech} (z),}   con   $${\ displaystyle \ operatorname {sech} (z) = {\ frac {1} {\ cosh (z)}}.

Aquí sinh, cosh, tanh y sech son funciones hiperbólicas . En el límite m  = 1:

$${\ displaystyle \ operatorname {cn} \ left (z | m \ right) \ to \ operatorname {sech} (z),

con sech ( z ) = 1 / cosh ( z ).

Además, para el mismo límite de m  → 1, la integral elíptica completa del primer tipo K ( m ) va al infinito, mientras que la integral elíptica completa del segundo tipo E ( m ) va a uno. ^[23] Esto implica que los valores límite de la velocidad de fase c y la elevelación mínima η _{2 se} convierten en: ^[24]

$${\ displaystyle c = {\ sqrt {g \, h}} \, \ left (1 + {\ frac {1} {2}} \, {\ frac {H} {h}} \ right)}   y   $${\ displaystyle \ eta _ {2} = 0. \,}

En consecuencia, en términos del parámetro de ancho Δ , la solución de onda solitaria para la ecuación de KdV y BBM es: ^[24]

$${\ displaystyle \ eta (x, t) = H \, \ operatorname {sech} ^ {2} \ left ({\ frac {xc \, t} {\ Delta}} \ right).}

El parámetro de ancho, como se encontró para las ondas cnoidales y ahora en el límite m  → 1, es diferente para la ecuación de KdV y BBM: ^[24]

$${\ displaystyle \ Delta = h \, {\ sqrt {\ frac {4 \, h} {3 \, H}}}}	: Ecuación KdV, y
$${\ displaystyle \ Delta = h \, {\ sqrt {{\ frac {4 \, h} {3 \, H}} \, {\ frac {c} {\ sqrt {g \, h}}}}} }	: Ecuación de BBM.

Pero la velocidad de fase de la onda solitaria en ambas ecuaciones es la misma, para una cierta combinación de altura H y profundidad h .

Límite de altura de onda infinitesimal [ editar ]

Para infinitesimal altura de las olas se espera que los resultados de la teoría de las ondas cnoidal a converger hacia los de teoría de las ondas de Airy para el límite de las ondas largas λ  »  h . Primero se examinará la elevación de la superficie y, posteriormente, la velocidad de fase de las ondas cnoidales para la altura de onda infinitesimal.

Elevación de la superficie [ editar ]

espectáculo

  Detalles de la derivación.

Para la altura de onda infinitesimal , en el límite m  → 0, la elevación de superficie libre se convierte en:

$${\ displaystyle \ eta (x, t) = {\ tfrac {1} {2}} \, H \, \ cos \, \ theta,}   con   $${\ displaystyle \ theta = 2 \, \ pi \, {\ frac {\ xi} {\ lambda}} = 2 \, \ pi \ {\ frac {xc \, t} {\ lambda}}.}

Entonces, la amplitud de onda es ½ H , la mitad de la altura de la onda . Esta es de la misma forma que la estudiada en la teoría de ondas de Airy , pero tenga en cuenta que la teoría de ondas cnoidales solo es válida para ondas largas con su longitud de onda mucho más larga que la profundidad promedio del agua.

Velocidad de fase [ editar ]

espectáculo

  Detalles de la derivación.

Las velocidades de fase para la altura de onda infinitesimal, de acuerdo con las teorías de ondas cnoidales para la ecuación de KdV y la ecuación de BBM, son ^[31]

KdV	:	$${\ displaystyle c = {\ Bigl [} 1 - {\ tfrac {1} {6}} \, \ left (\ kappa h \ right) ^ {2} {\ Bigr]} \, {\ sqrt {g \ , h}},}
BBM	:	$${\ displaystyle c = {\ frac {1} {1 + {\ tfrac {1} {6}} \, \ left (\ kappa h \ right) ^ {2}}} \, {\ sqrt {g \, h}}

con κ  = 2 π  /  λ el número de onda y κh el número de onda relativo. Estas velocidades de fase están en total acuerdo con el resultado obtenido al buscar directamente soluciones de onda sinusoidal de las ecuaciones de KdV y BBM linealizadas. Como es evidente a partir de estas ecuaciones, la ecuación BBM linealizada tiene una velocidad de fase positiva para todos los κh . Por otro lado, la velocidad de fase de la ecuación KdV linealizada cambia de signo para ondas cortas con κh  > $${\ displaystyle \ scriptstyle {\ sqrt {6}}}. Esto está en conflicto con la derivación de la ecuación KdV como una ecuación de onda unidireccional.

Derivación directa de las ecuaciones de flujo inviscid completas [ editar ]

Diámetro irregular y cachorros cerca de la desembocadura del río Araguari en el noreste de Brasil. La vista es oblicua hacia la boca desde el avión a aproximadamente 100 pies (30 m) de altitud. ^[32]

Las ondas cnoidales se pueden derivar directamente de las ecuaciones de flujo inviscidas , irrotacionales e incompresibles , y se expresan en términos de tres invariantes del flujo, como lo demuestran Benjamin y Lighthill (1954) en su investigación sobre perforaciones irregulares . En un marco de referencia que se mueve con la velocidad de fase , en el que el flujo de referencia se convierte en un flujo constante , las soluciones de onda cnoidal se pueden relacionar directamente con el flujo de masa , el flujo de momento y la carga de energía del flujo. Siguiendo a Benjamin y Lighthill (1954), usando una función de transmisiónDescripción de este flujo incompresible: las componentes horizontales y verticales de la velocidad del flujo son las derivadas espaciales de la función de flujo Ψ ( ξ, z ): + ∂ _z Ψ y - ∂ _ξ Ψ , en la dirección ξ y z respectivamente ( ξ  =  x - ct ). La coordenada vertical z es positiva en la dirección hacia arriba, opuesta a la dirección de la aceleración gravitacional, y el nivel cero de z está en el límite inferior impermeable del dominio del fluido. Mientras que la superficie libre está en z =  ζ ( ξ ); tenga en cuenta que ζ es la profundidad del agua local, relacionada con la elevación de la superficie η ( ξ ) como ζ  =  h  +  η con h la profundidad media del agua.

En este flujo constante, la descarga Q a través de cada sección transversal vertical es una constante independiente de ξ , y debido al lecho horizontal también se conserva el flujo de momento horizontal S , dividido por la densidad ρ , a través de cada sección transversal vertical. Además, para este flujo inviscido e irrotacional, el principio de Bernoulli se puede aplicar y tiene la misma constante de Bernoulli R en todas partes en el dominio de flujo. Se definen como: ^[33]

{\ displaystyle {\ begin {alineado} Q & = \ int _ {0} ^ {\ zeta (\ xi)} \ partial _ {z} \ Psi \; {\ text {d}} z, \\ R & = { \ frac {p} {\ rho}} + {\ tfrac {1} {2}} \, {\ Bigl [} \ left (\ partial _ {\ xi} \ Psi \ right) ^ {2} + \ left (\ parcial _ {z} \ Psi \ derecha) ^ {2} {\ Bigr]} + g \, z \ qquad {\ text {y}} \\ S & = \ int _ {0} ^ {\ zeta ( \ xi)} \ left [{\ frac {p} {\ rho}} + \ left (\ partial _ {z} \ Psi \ right) ^ {2} \ right] \; {\ text {d}} z . \ end {alineado}}}

Para olas bastante largas, asumiendo que la profundidad del agua ζ es pequeña en comparación con la longitud de onda λ , se obtiene la siguiente relación entre la profundidad del agua ζ ( ξ ) y los tres invariantes Q , R y S : ^[33]

$${\ displaystyle {\ tfrac {1} {3}} \, Q ^ {2} \, \ left (\ zeta '\ right) ^ {2} \ approx -g \, \ zeta ^ {3} +2 \ , R \, \ zeta ^ {2} -2 \, S \, \ zeta + Q ^ {2}.}

( E )

Esta ecuación diferencial ordinaria no lineal y de primer orden tiene soluciones de ondas cnoidales.

Para ondas muy largas de amplitud infinitesimal en un fluido de profundidad h y con una velocidad de flujo vuniforme , las constantes de flujo están de acuerdo con las ecuaciones de aguas someras : ^[33]

$${\ displaystyle Q_ {0} = v \, h,}   $${\ displaystyle R_ {0} = {\ tfrac {1} {2}} \, v ^ {2} + g \, h}   y   $${\ displaystyle S_ {0} = v ^ {2} \, h + {\ tfrac {1} {2}} \, g \, h ^ {2}.}

La ecuación ( E ) se puede llevar a una forma no dimensional mediante el uso de la descarga Q y la aceleración gravitacional g , y definiendo la profundidad crítica h _c :

$${\ displaystyle h_ {c} = {\ sqrt [{3}] {\ frac {Q ^ {2}} {g}}},}

relacionado con la demarcación del flujo crítico entre el flujo subcrítico y el flujo supercrítico (véase también el número de Froude ). En consecuencia, la forma no dimensional de la ecuación es

$${\ displaystyle {\ tfrac {1} {3}} \, \ left ({\ tilde {\ zeta}} '\ right) ^ {2} \ approx - \ zeta ^ {3} +2 \, {\ tilde {R}} \, {\ tilde {\ zeta}} ^ {2} -2 \, {\ tilde {S}} \, {\ tilde {\ zeta}} + 1,}

con

$${\ displaystyle {\ tilde {\ zeta}} = {\ frac {\ zeta} {h_ {c}}},}   $${\ displaystyle {\ tilde {\ xi}} = {\ frac {\ xi} {h_ {c}}},}   $${\ displaystyle {\ tilde {R}} = {\ frac {R} {g \, h_ {c}}},}   y   $${\ displaystyle {\ tilde {S}} = {\ frac {S} {g \, h_ {c} ^ {2}}}.}

Derivación [ editar ]

Primero elimine la presión p del flujo de momento S mediante el uso de la ecuación de Bernoulli:

$${\ displaystyle S = R \, \ zeta - {\ tfrac {1} {2}} \, g \, \ zeta ^ {2} + \ int _ {0} ^ {\ zeta} {\ tfrac {1} {2}} \ left [\ left (\ partial _ {z} \ Psi \ right) ^ {2} - \ left (\ partial _ {\ xi} \ Psi \ right) ^ {2} \ right] \; {\ text {d}} z.}

La función de la corriente Ψ se expande como una serie de Maclaurin alrededor del lecho en z  = 0, y utilizando que el lecho impermeable es una línea de corriente y la irrotacionalidad del flujo: Ψ  = 0 y ∂ _z ² Ψ  = 0 en z  = 0: ^{[33 ]}

$${\ displaystyle \ Psi = z \, u_ {b} (\ xi) - {\ frac {z ^ {3}} {3!}} \, u_ {b} '' (\ xi) + {\ frac { z ^ {5}} {5!}} \, u_ {b} ^ {\ text {iv}} (\ xi) + \ cdots,}

con u _b la velocidad horizontal en la cama z  = 0. Debido a que las ondas son largas, h  »  λ , sólo los términos hasta z ³ y ζ ³ son retenidos en las aproximaciones a Q y S . El flujo de impulso S se convierte entonces en: ^[33]

$${\ displaystyle S = R \, \ zeta - {\ tfrac {1} {2}} \, g \, \ zeta ^ {2} + {\ tfrac {1} {2}} \, \ zeta \, u_ {b} ^ {2} - {\ tfrac {1} {6}} \, \ zeta ^ {3} \, u_ {b} \, u_ {b} '' - {\ tfrac {1} {6} } \, \ zeta ^ {3} \, \ left (u_ {b} '\ right) ^ {2} + \ cdots.}

La descarga Q se convierte en, ya que es el valor de la función de flujo Ψ en la superficie libre z  =  ζ :

$${\ displaystyle Q = \ zeta \, u_ {b} (\ xi) - {\ tfrac {1} {6}} \, \ zeta ^ {3} \, u_ {b} '' {\ xi} + \ cdots.}

Como puede verse, la descarga Q es un O ( ζ cantidad). A partir de esto, la velocidad del lecho se ve como ^[33]

$${\ displaystyle u_ {b} = {\ frac {Q} {\ zeta}} + {\ tfrac {1} {6}} \, \ zeta ^ {2} \, u_ {b} '' + \ cdots. }

Tenga en cuenta que Q  /  ζ es una cantidad de un pedido. Esta relación se puede utilizar para sustituir la velocidad de la cama u _b por Q y ζ en el flujo del impulso S . Los siguientes términos se pueden derivar de él:

{\ displaystyle {\ begin {alineado} u_ {b} ^ {2} & = {\ frac {Q ^ {2}} {\ zeta ^ {2}}} + {\ tfrac {1} {3}} \ , \ zeta \, Q \, u_ {b} '' + \ cdots, \\ u_ {b} '& = - {\ frac {Q} {\ zeta}} \, \ zeta' + {\ tfrac {1 } {3}} \, \ zeta \, \ zeta '\, u_ {b}' '+ {\ tfrac {1} {6}} \, \ zeta ^ {2} \, u_ {b}' '' + \ cdots \ qquad {\ text {and}} \\\ left (u_ {b} '\ right) ^ {2} & = {\ frac {Q ^ {2}} {\ zeta ^ {4}}} \, \ left (\ zeta '\ right) ^ {2} - {\ tfrac {2} {3}} \, {\ frac {Q} {\ zeta}} \, \ zeta' \, u_ {b} '' + \ cdots. \ end {alineado}}}

En consecuencia, el flujo de impulso S se convierte, de nuevo, reteniendo solo los términos hasta proporcional a ζ ³ : ^[33]

$${\ displaystyle S \ approx R \, \ zeta - {\ tfrac {1} {2}} \, g \, \ zeta ^ {2} + {\ tfrac {1} {2}} \, {\ frac { Q ^ {2}} {\ zeta}} - {\ tfrac {1} {6}} \, {\ frac {Q ^ {2}} {\ zeta}} \, \ left (\ zeta '\ right) ^ {2}.}

Que se puede refundir directamente en forma de ecuación ( E ).

Energía potencial [ editar ]

La densidad de energía potencial.

$${\ displaystyle E _ {\ text {pot}} = {\ frac {1} {\ lambda}} \, \ int _ {0} ^ {\ lambda} {\ tfrac {1} {2}} \, \ rho \, g \, \ eta ^ {2} (x, t) \; {\ text {d}} x}

con ρ la densidad del fluido , es uno de los infinitos invariantes de la ecuación de KdV. ^[34] Esto se puede ver al multiplicar la ecuación de KdV con la elevación de la superficie η ( x , t ); después del uso repetido de la regla de la cadena el resultado es:

$${\ displaystyle \ partial _ {t} \ left ({\ tfrac {1} {2}} \, \ eta ^ {2} \ right) + \ partial _ {x} \ left \ {{\ tfrac {1} {2}} \, {\ sqrt {g \, h}} \, \ eta ^ {2} + {\ tfrac {1} {2}} \, {\ sqrt {\ frac {g} {h}} } \, \ eta ^ {3} + {\ tfrac {1} {12}} \, h ^ {2} {\ sqrt {g \, h}} \, \ left [\ partial _ {x} ^ { 2} \ left (\ eta ^ {2} \ right) -3 \ left (\ partial _ {x} \ eta \ right) ^ {2} \ right] \ right \} = 0,}

que se encuentra en forma de conservación y es invariante después de la integración en el intervalo de periodicidad, la longitud de onda para una onda cnoidal. La energía potencial no es una invariante de la ecuación BBM, pero ½ ρg  [ η ²  +  ¹ / ₆ h ²  ( ∂ _x η ) ² ] es. ^[35]  

Primero se calcula la varianza de la elevación de la superficie en una onda cnoidal. Tenga en cuenta que η ₂  = - (1 / λ )  ₀ ∫ ^λ  H  cn ² ( ξ / Δ | m) d x , cn ( ξ / Δ | m) = cos  ψ ( ξ ) y λ  = 2  Δ  K ( m ) así que ^[36]

${\displaystyle {\begin{aligned}{\frac {1}{\lambda }}\,\int _{0}^{\lambda }\eta ^{2}\;{\text{d}}x&={\frac {1}{\lambda }}\int _{0}^{\lambda }\left\{\eta _{2}+H\,\operatorname {cn} ^{2}\left({\begin{array}{c|c}\displaystyle {\frac {\xi }{\Delta }}&m\end{array}}\right)\right\}^{2}\;{\text{d}}\xi ={\frac {H^{2}}{\lambda }}\int _{0}^{\lambda }\operatorname {cn} ^{4}\left({\begin{array}{c|c}\displaystyle {\frac {\xi }{\Delta }}&m\end{array}}\right)\;{\text{d}}\xi -\eta _{2}^{2}\\&={\frac {\Delta \,H^{2}}{\lambda }}\int _{0}^{\pi }\cos ^{4}\,\psi \,{\frac {{\text{d}}\xi }{{\text{d}}\psi }}\;{\text{d}}\psi -\eta _{2}^{2}={\frac {H^{2}}{2\,K(m)}}\int _{0}^{\pi }{\frac {\cos ^{4}\,\psi }{\sqrt {1-m\,\sin ^{2}\,\psi }}}\;{\text{d}}\psi -\eta _{2}^{2}\\&={\frac {1}{3}}\,{\frac {H^{2}}{m^{2}}}\,\left[\left(2-5\,m+3\,m^{2}\right)+\left(4\,m-2\right)\,{\frac {E(m)}{K(m)}}\right]-{\frac {H^{2}}{m^{2}}}\,\left(1-m-{\frac {E(m)}{K(m)}}\right)^{2}\end{aligned}}}$

La energía potencial, tanto para KdV como para la ecuación de BBM, se encuentra posteriormente en ^[36]

$${\ displaystyle E _ {\ text {pot}} = {\ tfrac {1} {2}} \, \ rho \, g \, H ^ {2} \, \ left [- {\ frac {1} {3 \, m}} + {\ frac {2} {3 \, m}} \, \ left (1 + {\ frac {1} {m}} \ right) \ left (1 - {\ frac {E ( m)} {K (m)}} \ right) - {\ frac {1} {m ^ {2}}} \, \ left (1 - {\ frac {E (m)} {K (m)} } \ right) ^ {2} \ right].}

El límite de onda altura infinitesimal ( m  → 0) de la energía potencial es E _olla  =  ¹ / ₁₆ ρ g H ² , que está de acuerdo con la teoría de onda de Airy . ^[36] La altura de la onda es el doble de la amplitud, H  = 2 a , en el límite de onda infinitesimal.