OCEANOGRAFÍA FÍSICA

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Cruce del oleaje en Île de Ré .

Vista de los aviones del mar cruzado cerca de lisboa .

Un mar cruz es un estado de la mar de las olas del mar generadas por el viento que se forman sistemas de ondas no paralelas. Cruzar los mares tiene una gran cantidad de propagación direccional. ^[1]Esto puede ocurrir cuando las ondas de agua de un sistema meteorológico continúan a pesar de un cambio en el viento . Las ondas generadas por el nuevo viento corren en ángulo con el viejo.

Dos sistemas meteorológicos que están alejados entre sí pueden crear un mar cruzado cuando las olas de los sistemas se encuentran, por lo general en un lugar alejado de cualquier sistema meteorológico. Hasta que las olas más viejas se hayan disipado, crean un peligro peligroso para el mar.

Este estado de mar es bastante común y se encontró que un gran porcentaje de accidentes de barcos ocurrieron en este estado. ^[2]Los buques se comportan mejor contra las olas grandes cuando están perpendiculares a las olas. En un mar cruzado, es más probable que los barcos sean golpeados de una manera peligrosa. ^[3]

A oleaje transversal se genera cuando los sistemas de olas son más largo período hinche , en lugar de las ondas generadas por el viento de período corto.

dispersión de las ondas de agua generalmente se refiere a la dispersión de frecuencia , lo que significa que las ondas de diferentes longitudes de onda viajan a diferentes velocidades de fase . Las ondas de agua, en este contexto, son ondas que se propagan en la superficie del agua , con la gravedad y la tensión superficial como fuerzas de restauración . Como resultado, el agua con una superficie libregeneralmente se considera un medio dispersivo .

Para una cierta profundidad del agua, las ondas de gravedad de la superficie , es decir, las ondas que se producen en la interfaz aire-agua y la gravedad como la única fuerza que la restaura a la planitud, se propagan más rápido a medida que aumenta la longitud de onda . Por otro lado, para una longitud de onda determinada (fija), las ondas de gravedad en aguas más profundas tienen una mayor velocidad de fase que en aguas menos profundas . ^[1] En contraste con el comportamiento de las ondas de gravedad, las ondas capilares (es decir, solo forzadas por la tensión superficial) se propagan más rápido para longitudes de onda más cortas.

Además de la dispersión de frecuencia, las ondas de agua también exhiben dispersión de amplitud. Este es un efecto no lineal , por el cual las ondas de mayor amplitud tienen una velocidad de fase diferente de las ondas de pequeña amplitud.

Dispersión de frecuencia para ondas de gravedad de superficie [ editar ]

Esta sección trata sobre la dispersión de frecuencia para ondas en una capa fluida forzada por la gravedad y de acuerdo con la teoría lineal. Para los efectos de tensión superficial en la dispersión de frecuencia, vea los efectos de tensión superficial en la teoría de ondas aereas y la onda capilar .

Propagación de la onda y la dispersión [ editar ]

Onda sinusoidal.

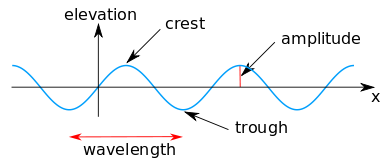
La onda de propagación más simple de forma inmutable es una onda sinusoidal . Una onda sinusoidal con elevación de la superficie del agua η (x, t) viene dada por: ^[2]

$${\ displaystyle \ eta (x, t) = a \ sin \ left (\ theta (x, t) \ right), \,}

donde a es la amplitud (en metros) y θ = θ (x, t) es la función de fase (en radianes ), según la posición horizontal (  x  , en metros) y el tiempo (  t  , en segundos ): ^[3]

$${\ displaystyle \ theta = 2 \ pi \ left ({\ frac {x} {\ lambda}} - {\ frac {t} {T}} \ right) = kx- \ omega t,}   con   $${\ displaystyle k = {\ frac {2 \ pi} {\ lambda}}}   y   $${\ displaystyle \ omega = {\ frac {2 \ pi} {T}},}

dónde:

• λ es la longitud de onda (en metros),
• T es el periodo (en segundos),
• k es el número de onda (en radianes por metro) y
• ω es la frecuencia angular (en radianes por segundo).

Las fases características de una ola de agua son:

• el cruce por cero hacia arriba en θ = 0 ,
• la cresta de la ola en θ =  ½  π ,
• el cruce por cero hacia abajo en θ = π y
• el canal de onda en θ = 1½ π .

Una cierta fase se repite después de un entero m múltiplo de 2π : sin ( θ ) = sin ( θ + m • 2π ).

Esencial para las ondas de agua, y otros fenómenos de onda en la física , que las ondas de propagación libre de amplitud no nula solo existen cuando la frecuencia angular ω y el número de onda k (o equivalentemente la longitud de onda λ y el período T ) satisfacen una relación funcional : la dispersión de frecuencia relación ^[4] [5]

$${\ displaystyle \ omega ^ {2} = \ Omega ^ {2} (k). \,}

La relación de dispersión tiene dos soluciones: ω = + Ω (k) y ω = −Ω (k) , correspondientes a ondas que viajan en la dirección x positiva o negativa . La relación de dispersión en general dependerá de varios otros parámetros además del número de onda k . Para las ondas de gravedad, de acuerdo con la teoría lineal, estas son la aceleración por gravedad gy la profundidad del agua h . La relación de dispersión para estas ondas es: ^[6] [5]

$${\ displaystyle \ omega ^ {2} = g \, k \, \ tanh (k \, h)}   o   $${\ displaystyle \ displaystyle \ lambda = {\ frac {g} {2 \ pi}} \, T ^ {2} \, \ tanh \ left (2 \ pi \, {\ frac {h} {\ lambda}} \Correcto),}

una ecuación implícita con tanh que denota la función tangente hiperbólica .

Una fase de onda inicial θ = θ _{0 se} propaga en función del espacio y el tiempo . Su posición posterior está dada por:

$${\ displaystyle x = {\ frac {\ lambda} {T}} \, t + {\ frac {\ lambda} {2 \ pi}} \, \ theta _ {0} = {\ frac {\ omega} {k }} \, t + {\ frac {\ theta _ {0}} {k}}.}

Esto muestra que la fase se mueve con la velocidad: ^[2]

$${\ displaystyle c_ {p} = {\ frac {\ lambda} {T}} = {\ frac {\ omega} {k}} = {\ frac {\ Omega (k)} {k}},}

que se llama la velocidad de fase.

Velocidad de fase [ editar ]

Más información: Velocidad de la fase.

Dispersión de ondas de gravedad sobre una superficie fluida. Velocidad de la fase y del grupo dividida por la velocidad de la fase de aguas poco profundas √ gh en función de la profundidad relativa h / λ .  Líneas azules (A): velocidad de fase; Líneas rojas (B): velocidad de grupo; Línea discontinua negra (C): velocidad de fase y grupo √ gh válida en aguas poco profundas.  Líneas dibujadas: relación de dispersión válida en profundidad arbitraria.  Líneas discontinuas (azul y rojo): límites de aguas profundas.

Dispersión de ondas de gravedad sobre una superficie fluida. Velocidad de fase y grupo dividida por velocidad de fase de aguas profundas √ gλ  / (2 π ) en función de la profundidad relativa h  /  λ .  Líneas azules (A): velocidad de fase; Líneas rojas (B): velocidad de grupo; Línea discontinua negra (C): velocidad de fase y grupo √ gh válida en aguas poco profundas.  Líneas dibujadas: relación de dispersión válida en profundidad arbitraria.  Líneas discontinuas (azul y rojo): límites de aguas profundas.

Una onda sinusoidal , de pequeña amplitud de elevación de superficie y con una longitud de onda constante , se propaga con la velocidad de fase , también llamada velocidad de fase o celeridad. Mientras que la velocidad de fase es un vector y tiene una dirección asociada, celeridad o velocidad de fase se refieren solo a la magnitud de la velocidad de fase. De acuerdo con la teoría lineal para las ondas forzadas por la gravedad, la velocidad de fase depende de la longitud de onda y la profundidad del agua. Para una profundidad de agua fija, las ondas largas (con una longitud de onda grande) se propagan más rápido que las ondas más cortas.

En la figura de la izquierda, se puede ver que las ondas de aguas poco profundas , con longitudes de onda λmucho mayores que la profundidad del agua h , viajan con la velocidad de fase ^[2]

$${\ displaystyle c_ {p} = {\ sqrt {gh}} \ qquad \ scriptstyle {\ text {(agua poco profunda),}} \,}

con g la aceleración por gravedad y c _p la velocidad de fase. Dado que esta velocidad de fase en aguas poco profundas es independiente de la longitud de onda, las ondas de aguas poco profundas no tienen dispersión de frecuencia.

Utilizando otra normalización para la misma relación de dispersión de frecuencia, la figura de la derecha muestra que para una longitud de onda fija λ la velocidad de fase c _p aumenta al aumentar la profundidad del agua. ^[1]Hasta que, en aguas profundas con profundidad de agua h mayor que la mitad de la longitud de onda λ (así, para h / λ> 0.5 ), la velocidad de fase c _p es independiente de la profundidad de agua: ^[2]

$${\ displaystyle c_ {p} = {\ sqrt {\ frac {g \ lambda} {2 \ pi}}} = {\ frac {g} {2 \ pi}} T \ qquad \ scriptstyle {\ text {(profundo agua),}}}

con T el período de onda (el recíproco de la frecuencia f , T = 1 / f ). Así que en aguas profundas, la velocidad de fase aumenta con la longitud de onda y con el período.

Dado que la velocidad de fase satisface c _p  = λ / T = λf , la longitud de onda y el período (o frecuencia) están relacionados. Por ejemplo, en aguas profundas:

$${\ displaystyle \ lambda = {\ frac {g} {2 \ pi}} T ^ {2} \ qquad \ scriptstyle {\ text {(agua profunda).}}}

Las características de dispersión para profundidad intermedia se dan a continuación.

Velocidad de grupo [ editar ]

Más información: Velocidad de grupo.

Dispersión de frecuencia en grupos bicromáticos de ondas de gravedad en la superficie de aguas profundas. El cuadrado rojo se mueve con la velocidad de fase y los círculos verdes se propagan con la velocidad de grupo.

mostrarmás…

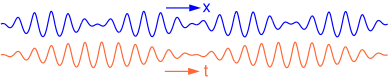
La interferencia de dos ondas sinusoidales con longitudes de onda ligeramente diferentes, pero la misma amplitud y dirección de propagación, da como resultado un patrón de latido , denominado grupo de ondas. Como se puede ver en la animación, el grupo se mueve con una velocidad de grupo c _gdiferente de la velocidad de fase c _p , debido a la dispersión de frecuencia.

La velocidad del grupo está representada por las líneas rojas (marcadas con B ) en las dos figuras de arriba. En aguas poco profundas, la velocidad de grupo es igual a la velocidad de la fase de aguas poco profundas. Esto se debe a que las ondas de aguas someras no son dispersivas. En aguas profundas, la velocidad de grupo es igual a la mitad de la velocidad de fase: c _g  = ½ c _p . ^[7]

La velocidad de grupo también resulta ser la velocidad de transporte de energía. Esta es la velocidad con la que la energía de onda media se transporta horizontalmente en un campo de onda de banda estrecha . ^[8] [9]

En el caso de una velocidad de grupo diferente de la velocidad de fase, una consecuencia es que el número de ondas contadas en un grupo de ondas es diferente cuando se cuenta desde una instantánea en el espacio en un momento determinado, desde cuando se cuenta en el tiempo desde la elevación de la superficie medida en una posición fija. Consideremos un grupo de ondas de longitud Λ _g y la duración grupo de τ _g . La velocidad del grupo es: ^[10]

$${\ displaystyle c_ {g} = {\ frac {\ Lambda _ {g}} {\ tau _ {g}}}.}

El número de ondas por grupo como se observa en el espacio en un momento determinado (línea azul superior), es diferente del número de ondas por grupo visto en el tiempo en una posición fija (línea naranja inferior), debido a la dispersión de frecuencia.

mostrarmás…

Las tormentas del Pacífico Norte se ven desde NOAA M / V Noble Star, invierno de 1989.

El número de ondas en un grupo de ondas, medido en el espacio en un momento determinado es: Λ _g  / λ . Mientras que se mide en una ubicación fija en el tiempo, el número de ondas en un grupo es: τ _g  / T . Entonces, la proporción del número de ondas medidas en el espacio con respecto a las medidas en el tiempo es:

$${\ displaystyle {\ tfrac {\ text {No. de ondas en el espacio}} {\ text {No. de ondas en el tiempo}}} = {\ frac {\ Lambda _ {g} / \ lambda} {\ tau _ {g} / T}} = {\ frac {\ Lambda _ {g}} {\ tau _ { g}}} \ cdot {\ frac {T} {\ lambda}} = {\ frac {c_ {g}} {c_ {p}}}.}

Entonces, en aguas profundas, con c _g = ½ c _p , ^[11] un grupo de olas tiene el doble de olas en el tiempo que en el espacio. ^[12]

La elevación de la superficie del agua η (x, t) , como una función de la posición horizontal x y el tiempo t , para un grupo de ondas bicromáticas de modulación completa se puede formular matemáticamente como: ^[11]

$${\ displaystyle \ eta = a \, \ sin \ left (k_ {1} x- \ omega _ {1} t \ right) + a \, \ sin \ left (k_ {2} x- \ omega _ {2 } t \ right),}

con:

• a la amplitud de onda de cada componente de frecuencia en metros,
• k ₁ y k ₂ el número de onda de cada componente de onda, en radianes por metro, y
• ω ₁ y ω ₂ la frecuencia angular de cada componente de onda, en radianes por segundo.

Tanto ω ₁ como k ₁ , así como ω ₂ y k ₂ , deben satisfacer la relación de dispersión:

$${\ displaystyle \ omega _ {1} ^ {2} = \ Omega ^ {2} (k_ {1}) \,}   y   $${\ displaystyle \ omega _ {2} ^ {2} = \ Omega ^ {2} (k_ {2}). \,}

Usando identidades trigonométricas , la elevación de la superficie se escribe como: ^[10]

$${\ displaystyle \ eta = \ left [2 \, a \, \ cos \ left ({\ frac {k_ {1} -k_ {2}} {2}} x - {\ frac {\ omega _ {1} - \ omega _ {2}} {2}} t \ right) \ right] \; \ cdot \; \ sin \ left ({\ frac {k_ {1} + k_ {2}} {2}} x- {\ frac {\ omega _ {1} + \ omega _ {2}} {2}} t \ right).

La parte entre corchetes es la amplitud de variación lenta del grupo, con el número de onda del grupo ½ (k ₁  - k ₂ ) y la frecuencia angular del grupo ½ (ω ₁  - ω ₂  ) . Como resultado, la velocidad del grupo es, para el límite k ₁ → k ₂  : ^[10] [11]

$${\ displaystyle c_ {g} = \ lim _ {k_ {1} \, \ to \, k_ {2}} {\ frac {\ omega _ {1} - \ omega _ {2}} {k_ {1} -k_ {2}}} = \ lim _ {k_ {1} \, \ to \, k_ {2}} {\ frac {\ Omega (k_ {1}) - \ Omega (k_ {2})} { k_ {1} -k_ {2}}} = {\ frac {{\ text {d}} \ Omega (k)} {{\ text {d}} k}}.}

Los grupos de ondas solo se pueden discernir en el caso de una señal de banda estrecha, con la diferencia de número de onda k ₁  - k ₂ pequeña en comparación con el número medio de onda ½ (k ₁  + k ₂ ) .

Patrones de onda de componentes múltiples [ editar ]

Dispersión de frecuencia de las ondas de gravedad superficial en aguas profundas. Se muestra la superposición (línea azul oscuro) de tres componentes de onda sinusoidal (líneas azul claro).

mostrarmás…

El efecto de la dispersión de frecuencia es que las ondas viajan en función de la longitud de onda, de modo que las propiedades de las fases espaciales y temporales de la onda de propagación cambian constantemente. Por ejemplo, bajo la acción de la gravedad, las ondas de agua con una longitud de onda más larga viajan más rápido que aquellas con una longitud de onda más corta.

Mientras que dos ondas sinusoidales superpuestas, llamadas ondas bicromáticas, tienen una envoltura que viaja sin cambios, tres o más componentes de ondas sinusoidales dan como resultado un patrón cambiante de las ondas y su envoltura. Un estado de mar , es decir, olas reales en el mar o el océano, se puede describir como una superposición de muchas olas sinusoidales con diferentes longitudes de onda, amplitudes, fases iniciales y direcciones de propagación. Cada uno de estos componentes viaja con su propia velocidad de fase, de acuerdo con la relación de dispersión. Las estadísticas de dicha superficie se pueden describir por su espectro de potencia . ^[13]

Relación de dispersión [ editar ]

En la siguiente tabla, se proporciona la relación de dispersión ω ² = [ Ω (k) ] ² entre la frecuencia angular ω = 2π / T y el número de onda k = 2π / λ , así como las velocidades de fase y grupo. ^[10]

Dispersión de frecuencia de las ondas de gravedad en la superficie de aguas profundas, aguas poco profundas y en profundidades intermedias, según la teoría de la onda lineal
cantidad	símbolo	unidades	agua profunda  ( h > ½ λ )	aguas poco profundas  ( h <0 .05="" font="" nbsp="">λ )	profundidad intermedia  (todas λ y h )
relación de dispersión	$${\ displaystyle \ displaystyle \ Omega (k)}	rad / s	$${\ displaystyle {\ sqrt {gk}} = {\ sqrt {\ frac {2 \ pi \, g} {\ lambda}}}}	$${\ displaystyle k {\ sqrt {gh}} = {\ frac {2 \ pi} {\ lambda}} {\ sqrt {gh}}}	{\ displaystyle {\ begin {alineado} & {\ sqrt {gk \, \ tanh \ left (kh \ right)}} \, \\ [1.2ex] & = {\ sqrt {{\ frac {2 \ pi g } {\ lambda}} \ tanh \ left ({\ frac {2 \ pi h} {\ lambda}} \ right)}} \, \ end {alineado}}}
velocidad de fase	$${\ displaystyle \ displaystyle c_ {p} = {\ frac {\ lambda} {T}} = {\ frac {\ omega} {k}}}	Sra	$${\ displaystyle {\ sqrt {\ frac {g} {k}}} = {\ frac {g} {\ omega}} = {\ frac {g} {2 \ pi}} T}	$${\ displaystyle {\ sqrt {gh}}}	$${\ displaystyle {\ sqrt {{\ frac {g} {k}} \ tanh \ left (kh \ right)}}}
velocidad de grupo	$${\ displaystyle \ displaystyle c_ {g} = {\ frac {\ partial \ Omega} {\ partial k}}}	Sra	$${\ displaystyle {\ frac {1} {2}} {\ sqrt {\ frac {g} {k}}} = {\ frac {1} {2}} {\ frac {g} {\ omega}} = {\ frac {g} {4 \ pi}} T}	$${\ displaystyle {\ sqrt {gh}}}	$${\ displaystyle {\ frac {1} {2}} c_ {p} \ left (1 + {\ frac {2kh} {\ sinh \ left (2kh \ right)}} \ right)}
proporción	$${\ displaystyle \ displaystyle {\ frac {c_ {g}} {c_ {p}}}}	-	$${\ displaystyle \ displaystyle {\ frac {1} {2}}}	$${\ displaystyle \ displaystyle 1}	$${\ displaystyle {\ frac {1} {2}} \ left (1 + {\ frac {2kh} {\ sinh \ left (2kh \ right)}} \ right)}
longitud de onda	$${\ displaystyle \ displaystyle \ lambda}	metro	$${\ displaystyle {\ frac {g} {2 \ pi}} T ^ {2}}	$${\ displaystyle T {\ sqrt {gh}}}	Para el período T dado , la solución de: $${\ displaystyle \ displaystyle \ left ({\ frac {2 \ pi} {T}} \ right) ^ {2} = {\ frac {2 \ pi g} {\ lambda}} \ tanh \ left ({\ frac {2 \ pi h} {\ lambda}} \ derecha)}

Las aguas profundas se corresponden con profundidades de agua mayores a la mitad de la longitud de onda , que es la situación común en el océano. En aguas profundas, las olas de períodos más largos se propagan más rápido y transportan su energía más rápido. La velocidad del grupo de aguas profundas es la mitad de la velocidad de fase . En aguas poco profundas , para longitudes de onda mayores a veinte veces la profundidad del agua, ^[14] como se encuentra muy a menudo cerca de la costa, la velocidad del grupo es igual a la velocidad de la fase.

Historia [ editar ]

La relación de dispersión lineal completa fue encontrada por primera vez por Pierre-Simon Laplace , aunque hubo algunos errores en su solución para el problema de la onda lineal. La teoría completa para las ondas de agua lineales, incluida la dispersión, fue derivada por George Biddell Airy y publicada alrededor de 1840. Philip Kelland también encontró una ecuación similar aproximadamente al mismo tiempo (pero cometiendo algunos errores en su derivación de la teoría de la onda) . ^[15]

El límite de aguas poco profundas (con un pequeño límite h / λ ), ω ² = gh k ² , fue derivado por Joseph Louis Lagrange .

Efectos de tensión superficial [ editar ]

Más información: Onda capilar.

Dispersión de las ondas gravitacionales-capilares sobre la superficie de las aguas profundas. Velocidad de fase y grupo dividida por$${\ displaystyle \ scriptstyle {\ sqrt [{4}] {g \ sigma / \ rho}}} en función de la longitud de onda relativa inversa $${\ displaystyle \ scriptstyle {\ frac {1} {\ lambda}} {\ sqrt {\ sigma / (\ rho g)}}}. 
Líneas azules (A): velocidad de fase, Líneas rojas (B): velocidad de grupo. 
Líneas dibujadas: relación de dispersión para las ondas gravitacionales-capilares. 
Líneas discontinuas: relación de dispersión para ondas de gravedad de aguas profundas. 
Líneas de puntos y puntos: relación de dispersión válida para ondas capilares de aguas profundas.

En el caso de ondas gravitacionales-capilares, donde la tensión superficial afecta a las ondas, la relación de dispersión se convierte en: ^[5]

$${\ displaystyle \ omega ^ {2} = \ left (gk + {\ frac {\ sigma} {\ rho}} k ^ {3} \ right) \ tanh (kh),}

con σ la tensión superficial (en N / m).

Para una interfaz agua-aire (con σ = 0.074 N / m y ρ = 1000 kg / m³ ), las ondas se pueden aproximar como ondas capilares puras, dominadas por efectos de tensión superficial, para longitudes de onda menores de 0.4 cm (0.2 in). Para longitudes de onda superiores a 7 cm (3 pulg.), Las ondas son de buena aproximación a ondas de gravedad pura de superficie con muy pocos efectos de tensión superficial. ^[dieciséis]

Ondas interfaciales [ editar ]

Movimiento ondulatorio en la interfaz entre dos capas de fluidos homogéneos no viscópicos de diferente densidad, confinados entre límites rígidos horizontales (en la parte superior e inferior). El movimiento es forzado por la gravedad. La capa superior tiene una profundidad media h ' y una densidad ρ' , mientras que la capa inferior tiene una profundidad media h y una densidad ρ . La amplitud de onda es a , la longitud de onda se denota por λ .

Para dos capas homogéneas de fluidos, de grosor medio h debajo de la interfaz y h ′ arriba: bajo la acción de la gravedad y limitadas por encima y por debajo por paredes rígidas horizontales, se proporciona la relación de dispersión ω ²  = Ω ² ( k ) para las ondas de gravedad por: ^[17]

$${\ displaystyle \ Omega ^ {2} (k) = {\ frac {g \, k (\ rho - \ rho ')} {\ rho \, \ coth (kh) + \ rho' \, \ coth (kh ')}},}

donde de nuevo, ρ y ρ ′ son las densidades por debajo y por encima de la interfaz, mientras que coth es la función cotangente hiperbólica . En el caso de que ρ ′ sea ​​cero, esto se reduce a la relación de dispersión de las ondas de gravedad de la superficie en el agua de profundidad finita h.

Cuando la profundidad de las dos capas de fluido se vuelve muy grande ( h → ∞, h ′ → ∞), los cotangentes hiperbólicos en la fórmula anterior se aproximan al valor de uno. Entonces:

$${\ displaystyle \ Omega ^ {2} (k) = {\ frac {\ rho - \ rho '} {\ rho + \ rho'}} \, g \, k.}

Efectos no lineales [ editar ]

Aguas poco profundas [ editar ]

Más información: onda cnoidal

Los efectos de la dispersión de la amplitud aparecen, por ejemplo, en la onda solitaria : una sola joroba de agua que viaja a velocidad constante en aguas poco profundas con un lecho horizontal. Tenga en cuenta que las ondas solitarias son casi solitones , pero no exactamente, después de la interacción de dos ondas solitarias (en colisión o adelantamientos), han cambiado un poco en amplitud y se deja un residuo oscilatorio. ^[18] La solución de solitón único de la ecuación de Korteweg – de Vries , de la altura de la onda H en la profundidad del agua h, lejos de la cresta de la onda, viaja con la velocidad:

$${\ displaystyle c_ {p} = c_ {g} = {\ sqrt {g (h + H)}}.}

Entonces, para esta onda de gravedad no lineal, es la profundidad total del agua debajo de la cresta de la onda lo que determina la velocidad, mientras que las ondas más altas viajan más rápido que las ondas más bajas. Tenga en cuenta que solo existen soluciones de onda solitaria para valores positivos de H , no existen ondas de gravedad solitarias de depresión.

Agua profunda [ editar ]

Más información: ola Stokes

La relación de dispersión lineal, no afectada por la amplitud de onda, es para ondas no lineales, también es correcta en el segundo orden de la expansión de la teoría de perturbación , con los órdenes en términos de la inclinación de la onda ka (donde a es la amplitud de onda ). Para el tercer orden, y para aguas profundas, la relación de dispersión es ^[19]

$${\ displaystyle \ omega ^ {2} = gk \ left [1+ (ka) ^ {2} \ right],   asi que   $${\ displaystyle c_ {p} = {\ sqrt {\ frac {g} {k}}} \, \ left [1 + {\ tfrac {1} {2}} \, (ka) ^ {2} \ right ] + {\ mathcal {O}} \ left ((ka) ^ {4} \ right).}

Esto implica que las ondas grandes viajan más rápido que las pequeñas de la misma frecuencia. Esto solo se nota cuando la inclinación de la onda ka es grande.

Ondas en una corriente media: Doppler shift [ editar ]

Las ondas de agua en un flujo medio (por lo tanto, una onda en un medio en movimiento) experimentan un cambio Doppler . Supongamos que la relación de dispersión para un medio sin movimiento es:

$${\ displaystyle \ omega ^ {2} = \ Omega ^ {2} (k), \,}

con k el wavenumber. Luego, para un medio con vector de velocidad media V , la relación de dispersión con el desplazamiento Doppler se convierte en: ^[20]

$${\ displaystyle \ left (\ omega - \ mathbf {k} \ cdot \ mathbf {V} \ right) ^ {2} = \ Omega ^ {2} (k),}

donde k es el vector wavenumber, relacionado con k como: k = | k |. El producto de puntos k • V es igual a: k • V = kV cos α , siendo V la longitud del vector de velocidad media V : V = | V |. Y α es el ángulo entre la dirección de propagación de la onda y la dirección del flujo medio. Para ondas y corriente en la misma dirección, k • V = kV .