En física teórica , los diagramas de Feynman son representaciones pictóricas de las expresiones matemáticas que describen el comportamiento de las partículas subatómicas . El esquema lleva el nombre de su inventor, el físico estadounidense Richard Feynman , y se introdujo por primera vez en 1948. La interacción de las partículas subatómicas puede ser compleja y difícil de entender intuitivamente. Los diagramas de Feynman brindan una visualización simple de lo que de lo contrario sería una fórmula abstracta y arcana. Como David Kaiserescribe, "desde mediados del siglo XX, los físicos teóricos han recurrido cada vez más a esta herramienta para ayudarles a realizar cálculos críticos", y por eso "los diagramas de Feynman han revolucionado casi todos los aspectos de la física teórica". [1] Si bien los diagramas se aplican principalmente a la teoría cuántica de campos , también se pueden usar en otros campos, como la teoría del estado sólido .
Feynman usó la interpretación de Ernst Stueckelberg del positrón como si fuera un electrón que retrocede en el tiempo. [2] Por lo tanto, las antipartículas se representan moviéndose hacia atrás a lo largo del eje del tiempo en los diagramas de Feynman.
El cálculo de las amplitudes de probabilidad en la física de partículas teórica requiere el uso de integrales bastante grandes y complicadas sobre un gran número de variables. Sin embargo, estas integrales tienen una estructura regular y pueden representarse gráficamente como diagramas de Feynman.
Un diagrama de Feynman es una contribución de una clase particular de trayectorias de partículas, que se unen y se dividen como se describe en el diagrama. Más precisamente, y técnicamente, un diagrama de Feynman es una representación gráfica de una contribución perturbativa a la amplitud de transición o función de correlación de una teoría cuántica del campo estadístico o mecánico. Dentro de la formulación canónica de la teoría cuántica de campos, un diagrama de Feynman representa un término en la expansión de Wick de la matriz S perturbativa . Alternativamente, la formulación integral del camino.La teoría cuántica de campos representa la amplitud de transición como una suma ponderada de todas las posibles historias del sistema desde el estado inicial hasta el final, en términos de partículas o campos. La amplitud de transición se da entonces como el elemento matriz de la matriz S entre los estados inicial y final del sistema cuántico.
Motivación e historia [ editar ]
Al calcular las secciones transversales de dispersión en la física de partículas , la interacción entre partículas se puede describir comenzando desde un campo libre que describe las partículas entrantes y salientes, e incluye una interacción hamiltoniana para describir cómo las partículas se desvían unas de otras. La amplitud para la dispersión es la suma de cada posible historial de interacción sobre todos los estados de partículas intermedias posibles. El número de veces que actúa la interacción hamiltoniana es el orden de expansión de la perturbación , y la teoría de la perturbación dependiente del tiempo para los campos se conoce como la serie Dyson . Cuando los estados intermedios en tiempos intermedios son estados propios deenergía.(colecciones de partículas con un impulso definido) la serie se denomina teoría de perturbación pasada de moda .
La serie Dyson puede ser alternativamente reescribirse como una suma sobre los diagramas de Feynman, donde en cada vértice tanto la energía y el impulso se conservan , pero donde la longitud de la energía-impulso de cuatro vector no es necesariamente igual a la masa. Los diagramas de Feynman son mucho más fáciles de seguir que los términos "pasados de moda", porque la manera anticuada trata las contribuciones de partículas y antipartículas por separado. Cada diagrama de Feynman es la suma de muchos términos pasados de moda exponencialmente, porque cada línea interna puede representar por separado una partícula o un antipartícula. En una teoría no relativista, no hay antipartículas y no hay duplicación, por lo que cada diagrama de Feynman incluye solo un término.
Feynman dio una receta para calcular la amplitud ( las reglas de Feynman, a continuación ) para cualquier diagrama dado de una teoría de campo lagrangiana . Cada línea interna corresponde a un factor de la partícula virtual 's propagador ; Cada vértice donde se unen las líneas da un factor derivado de un término de interacción en el Lagrangiano, y las líneas entrantes y salientes llevan una energía, un impulso y un giro .
Además de su valor como herramienta matemática, los diagramas de Feynman proporcionan una visión física profunda de la naturaleza de las interacciones de partículas. Las partículas interactúan en todas las formas disponibles; de hecho, las partículas virtuales intermedias pueden propagarse más rápido que la luz. La probabilidad de cada estado final se obtiene luego sumando todas estas posibilidades. Esto está estrechamente relacionado con la formulación integral funcional de la mecánica cuántica , también inventada por Feynman; consulte la formulación integral de la trayectoria .
La aplicación ingenua de tales cálculos a menudo produce diagramas cuyas amplitudes son infinitas , debido a que las interacciones de partículas a corta distancia requieren un procedimiento de limitación cuidadoso, para incluir auto-interacciones de partículas . La técnica de renormalización , sugerida por Ernst Stueckelberg y Hans Bethe e implementada por Dyson , Feynman, Schwinger y Tomonaga compensa este efecto y elimina los infinitos problemáticos. Después de la renormalización, los cálculos con diagramas de Feynman coinciden con los resultados experimentales con una precisión muy alta.
Los métodos integrales de diagrama y trayectoria de Feynman también se utilizan en la mecánica estadística e incluso se pueden aplicar a la mecánica clásica . [3]
Nombres alternativos [ editar ]
Murray Gell-Mann siempre se refirió a los diagramas de Feynman como diagramas de Stueckelberg , después de un físico suizo, Ernst Stueckelberg , quien ideó una notación similar muchos años antes. Stueckelberg estuvo motivado por la necesidad de un formalismo manifiestamente covariante para la teoría cuántica de campos, pero no proporcionó una forma tan automatizada de manejar los factores de simetría y los bucles, aunque fue el primero en encontrar la interpretación física correcta en términos de avance y retroceso en la partícula de tiempo. Caminos, todos sin el camino integral. [4]
Históricamente, como un dispositivo de contabilidad de la teoría de la perturbación covariante, los gráficos se denominaron diagramas de Feynman-Dyson o gráficos de Dyson , [5] porque la integral del camino no era familiar cuando se introdujeron, y la derivación de Freeman Dyson de la perturbación antigua. La teoría era más fácil de seguir para los físicos entrenados en métodos anteriores. [a] Feynman tuvo que presionar con fuerza para obtener los diagramas, lo que confundió a los físicos del establecimiento entrenados en ecuaciones y gráficos. [6]
Representación de la realidad física [ editar ]
En sus presentaciones de interacciones fundamentales , [7] [8] escritas desde la perspectiva de la física de partículas, Gerard 't Hooft y Martinus Veltman dieron buenos argumentos para tomar los diagramas originales de Feynman no regularizados como la representación más concisa de nuestro conocimiento actual sobre La física de la dispersión cuántica de partículas fundamentales . Sus motivaciones son consistentes con las convicciones de James Daniel Bjorken y Sidney Drell : [9]
Hasta ahora no hay opiniones opuestas. En las teorías de campos cuánticos, los diagramas de Feynman se obtienen de Lagrangian mediante las reglas de Feynman.
La regularización dimensional es un método para regularizar integrales en la evaluación de diagramas de Feynman; les asigna valores que son funciones meromorfas de un parámetro complejo auxiliar d , llamado la dimensión. La regularización dimensional escribe una integral de Feynman como una integral que depende de la dimensión d espacio-tiempo y los puntos espacio-tiempo.
La interpretación de las partículas de la ruta [ editar ]
Un diagrama de Feynman es una representación de los procesos de la teoría cuántica de campos en términos de interacciones de partículas . Las partículas están representadas por las líneas del diagrama, que pueden ser onduladas o rectas, con una flecha o sin ella, según el tipo de partícula. Un punto donde las líneas se conectan con otras líneas es un vértice , y aquí es donde las partículas se encuentran e interactúan: emitiendo o absorbiendo nuevas partículas, desviándose una a la otra o cambiando de tipo.
Hay tres tipos diferentes de líneas: las líneas internas conectan dos vértices, las líneas entrantes se extienden desde "el pasado" a un vértice y representan un estado inicial, y las líneas salientes se extienden desde un vértice hasta "el futuro" y representan el estado final (el las dos últimas también se conocen como líneas externas). Tradicionalmente, la parte inferior del diagrama es el pasado y la cima el futuro; otras veces, el pasado es a la izquierda y el futuro a la derecha. Al calcular funciones de correlación en lugar de dispersar amplitudes, no hay pasado ni futuro y todas las líneas son internas. Las partículas comienzan y terminan en las pequeñas x, que representan las posiciones de los operadores cuya correlación se está calculando.
Los diagramas de Feynman son una representación pictórica de una contribución a la amplitud total para un proceso que puede ocurrir de varias maneras diferentes. Cuando un grupo de partículas entrantes se dispersan unas con otras, el proceso puede pensarse como uno en el que las partículas viajan por todos los caminos posibles, incluidos los caminos que retroceden en el tiempo.
Los diagramas de Feynman a menudo se confunden con los diagramas del espacio-tiempo y las imágenes de la cámara de burbujas porque todos describen la dispersión de partículas. Los diagramas de Feynman son gráficosque representan la interacción de las partículas en lugar de la posición física de la partícula durante un proceso de dispersión. A diferencia de una imagen de cámara de burbujas, solo la suma de todos los diagramas de Feynman representa cualquier interacción de partículas dada; Las partículas no eligen un diagrama particular cada vez que interactúan. La ley de la suma está de acuerdo con el principio de superposición: cada diagrama contribuye a la amplitud total del proceso.
Descripción [ editar ]
Un diagrama de Feynman representa una contribución perturbativa a la amplitud de una transición cuántica de un estado cuántico inicial a un estado cuántico final.
Por ejemplo, en el proceso de aniquilación electrón-positrón, el estado inicial es un electrón y un positrón, el estado final: dos fotones.
A menudo se asume que el estado inicial está a la izquierda del diagrama y el estado final a la derecha (aunque también se usan otras convenciones con bastante frecuencia).
Un diagrama de Feynman consta de puntos, llamados vértices y líneas unidas a los vértices.
Las partículas en el estado inicial se representan mediante líneas que sobresalen en la dirección del estado inicial (por ejemplo, a la izquierda), las partículas en el estado final se representan mediante líneas que sobresalen en la dirección del estado final (por ejemplo, para el derecho).
En QED hay dos tipos de partículas: partículas de materia tales como electrones o positrones (llamados fermiones ) y partículas de intercambio (llamadas bosones gauge ). Están representados en los diagramas de Feynman de la siguiente manera:
- El electrón en el estado inicial se representa mediante una línea continua, con una flecha que indica el giro de la partícula, por ejemplo, apuntando hacia el vértice (→ •).
- El electrón en el estado final está representado por una línea, con una flecha que indica el giro de la partícula, por ejemplo, apuntando hacia afuera del vértice: (• →).
- El positrón en el estado inicial se representa mediante una línea continua, con una flecha que indica el giro de la partícula, por ejemplo, apuntando hacia el vértice: (← •).
- El positrón en el estado final está representado por una línea, con una flecha que indica el giro de la partícula, por ejemplo, apuntando hacia el vértice: (• ←).
- El fotón virtual en el estado inicial y final se representa mediante una línea ondulada ( ~ • y • ~ ).
En QED, un vértice siempre tiene tres líneas unidas: una línea bosónica, una línea fermiónica con flecha hacia el vértice y una línea fermiónica con flecha alejada del vértice.
Los vértices pueden estar conectados por un propagador bosónico o fermiónico . Un propagador bosónico está representado por una línea ondulada que conecta dos vértices (• ~ •). Un propagador fermiónico está representado por una línea continua (con una flecha en una u otra dirección) que conecta dos vértices, (• ← •).
El número de vértices da el orden del término en la expansión de la serie de perturbaciones de la amplitud de transición.
Ejemplo aniquilación electrón-positrón [ editar ]
La interacción de aniquilación electrón-positrón:
- e + e - → 2γ
tiene una contribución del diagrama de Feynman de segundo orden que se muestra adyacente:
En el estado inicial (en la parte inferior; tiempo temprano) hay un electrón (e - ) y un positrón (e + ) y en el estado final (en la parte superior; tiempo tardío) hay dos fotones (γ).
Formulación de cuantificación Canonical [ editar ]
La amplitud de probabilidad para una transición de un sistema cuántico desde el estado inicial | i ⟩ al estado final | f ⟩ está dado por el elemento de matriz
En la teoría del campo cuántico canónico, la S- matriz se representa dentro de la imagen de interacción por la serie de perturbaciones en los poderes de la interacción Lagrangiana,
donde L v es la interacción Lagrangiana y T significa el producto ordenado por el tiempo de los operadores.
Un diagrama de Feynman es una representación gráfica de un término en la expansión de Wick del producto tiempo-ordenada en el n º término de orden S ( n ) de la S -matrix,
donde N significa el producto normal de los operadores y (±) se encarga del posible cambio de señal al conmutar a los operadores fermiónicos para reunirlos para una contracción (un propagador ).
Reglas de Feynman [ editar ]
Los diagramas se dibujan de acuerdo con las reglas de Feynman, que dependen de la interacción de Lagrangian. Para la interacción QED Lagrangiana
describiendo la interacción de un campo fermiónico ψ con un campo gauge bosónico A μ , las reglas de Feynman se pueden formular en el espacio de coordenadas de la siguiente manera:
- Cada coordenada de integración x j está representada por un punto (a veces llamado vértice);
- Un propagador bosónico está representado por una línea ondulada que conecta dos puntos;
- Un propagador fermiónico está representado por una línea continua que conecta dos puntos;
- Un campo bosónico está representado por una línea ondulada unida al punto x i ;
- Un campo fermiónico ψ ( x i ) se representa mediante una línea continua unida al punto x i con una flecha hacia el punto;
- Un campo antifermiónico ψ ( x i ) se representa mediante una línea continua unida al punto x i con una flecha alejada del punto;
Ejemplo: procesos de segundo orden en QED [ editar ]
El término de perturbación de segundo orden en la matriz S es
Dispersión de fermiones [ editar ]
dónde
es la contracción electromagnética (propagador) en el indicador de Feynman. Este término está representado por el diagrama de Feynman a la derecha. Este diagrama da aportes a los siguientes procesos:
- e - e - dispersión (estado inicial a la derecha, estado final a la izquierda del diagrama);
- e + e + dispersión (estado inicial a la izquierda, estado final a la derecha del diagrama);
- e - e + dispersión (estado inicial en la parte inferior / superior, estado final en la parte superior / inferior del diagrama).
Distribución y aniquilación / generación de pares e - e + [ editar ]
Otro término interesante en la expansión es
dónde
Es la contracción fermiónica (propagador).
Formulación integral de ruta [ editar ]
En una integral de trayectoria , el campo lagrangiano, integrado en todos los historiales de campo posibles, define la amplitud de probabilidad para pasar de una configuración de campo a otra. Para que tenga sentido, la teoría de campo debe tener un estado fundamental bien definido , y la integral debe realizarse un poco girada en tiempo imaginario, es decir, una rotación de Wick .
Campo escalar lagrangiano [ editar ]
Un ejemplo simple es el campo escalar relativista libre en dimensiones d , cuya acción integral es:
La amplitud de probabilidad para un proceso es:
donde A y B son hipersuperficies en forma de espacio que definen las condiciones de contorno. La colección de todos los φ ( A ) en la hipersuperficie de inicio da el valor inicial del campo, análogo a la posición inicial para una partícula puntual, y los valores del campo φ ( B ) en cada punto de la hipersuperficie final definen el campo final valor, que se permite que varíe, dando una amplitud diferente para terminar en diferentes valores. Esta es la amplitud de transición campo a campo.
La integral de trayectoria da el valor esperado de los operadores entre el estado inicial y final:
y en el límite en que A y B retroceden al pasado infinito y al futuro infinito, la única contribución que importa es desde el estado fundamental (esto solo es rigurosamente cierto si la integral de trayectoria se define ligeramente girada en tiempo imaginario). Se puede considerar que la integral de trayectoria es análoga a una distribución de probabilidad, y es conveniente definirla para que la multiplicación por una constante no cambie nada:
El factor de normalización en la parte inferior se denomina función de partición para el campo, y coincide con la función de partición mecánica estadística a temperatura cero cuando se gira en tiempo imaginario.
Las amplitudes de inicial a final están mal definidas si uno piensa en el límite de continuidad desde el principio, porque las fluctuaciones en el campo pueden volverse ilimitadas. Por lo tanto, la integral de trayectoria se puede considerar como una red cuadrada discreta, con una separación de celosía a y el límite a → 0 debe tomarse con cuidado [ aclaración necesaria ] . Si los resultados finales no dependen de la forma de la red o del valor de a , entonces existe el límite continuo.
En una celosía [ editar ]
Aquí, el dominio de integración está sobre k restringido a un cubo de longitud de lado 2πa , por lo que no se permiten valores grandes de k . Es importante tener en cuenta que la medida k contiene los factores de 2 π de las transformadas de Fourier, esta es la mejor convención estándar para k -integrals en QFT. La red significa que las fluctuaciones en general k no pueden contribuir de inmediato, solo comienzan a contribuir en el límite a → 0 . A veces, en lugar de una celosía, los modos de campo se cortan a valores altos de k en su lugar.
También es conveniente, de vez en cuando, considerar que el volumen espacio-tiempo es finito, de modo que los modos k también son una red. Esto no es estrictamente tan necesario como el límite de la red espacial, ya que las interacciones en k no están localizadas, pero es conveniente para hacer un seguimiento de los factores frente a los k -integrals y las funciones delta que conservan el impulso que surgirán.
En una celosía, (ii), la acción debe ser discretizada:
donde ⟨ x , y ⟩ es un par de vecinos más cercanos de celosía x y y . Se debe considerar que la discretización define lo que significa la derivada ∂ μ φ .
En términos de los modos de Fourier de celosía, la acción se puede escribir:
Para k cerca de cero esto es:
Ahora tenemos la continua transformación de Fourier de la acción original. En volumen finito, la cantidad d d k no es infinitesimal, sino que se convierte en el volumen de una caja hecha por los modos de Fourier vecinos, o ( 2πV ) d
.
.
El campo φ tiene un valor real, por lo que la transformada de Fourier obedece:
En términos de partes reales e imaginarias, la parte real de φ ( k ) es una función par de k , mientras que la parte imaginaria es impar. La transformada de Fourier evita el doble conteo, para que pueda escribirse:
sobre un dominio de integración que se integra sobre cada par ( k , - k ) exactamente una vez.
Para un campo escalar complejo con acción.
la transformada de Fourier no está restringida:
y la integral es sobre todo k .
La integración sobre todos los diferentes valores de φ ( x ) es equivalente a la integración sobre todos los modos de Fourier, porque tomar una transformada de Fourier es una transformación lineal unitaria de coordenadas de campo. Cuando cambia las coordenadas en una integral multidimensional mediante una transformación lineal, el valor de la nueva integral viene dado por el determinante de la matriz de transformación. Si
entonces
Si A es una rotación, entonces
de modo que det A = ± 1 , y el signo depende de si la rotación incluye una reflexión o no.
La matriz que cambia las coordenadas de φ ( x ) a φ ( k ) se puede leer de la definición de una transformada de Fourier.
y el teorema de inversión de Fourier te dice lo inverso:
que es el complejo conjugado-transpuesto, hasta factores de 2 π . En una red de volumen finito, el determinante es distinto de cero e independiente de los valores de campo.
y la integral de trayectoria es un factor separado en cada valor de k .
El factor d d k es el volumen infinitesimal de una celda discreta en el espacio k , en una caja cuadrada cuadrada
donde L es la longitud lateral de la caja. Cada factor separado es un gaussiano oscilatorio, y el ancho de los gaussianos se desvía cuando el volumen va hasta el infinito.
En el tiempo imaginario, la acción euclidiana se vuelve positiva definida y puede interpretarse como una distribución de probabilidad. La probabilidad de que un campo tenga valores φ k es
El valor de expectativa del campo es el valor de expectativa estadística del campo cuando se elige de acuerdo con la distribución de probabilidad:
Dado que la probabilidad de φ k es un producto, el valor de φ k en cada valor separado de k se distribuye independientemente en Gauss. La varianza de Gauss es 1k 2 d d k , que es formalmente infinita, pero eso solo significa que las fluctuaciones son ilimitadas en volumen infinito. En cualquier volumen finito, la integral se reemplaza por una suma discreta, y la varianza de la integral es Vk 2 .

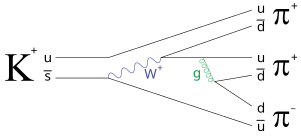



































No hay comentarios:
Publicar un comentario