ECUACIONES

LA TEORÍA DE HAZ DE EULER

Estrés [ editar ]

Además de la deflexión, la ecuación del haz describe las fuerzas y los momentos y, por lo tanto, puede utilizarse para describir las tensiones . Por esta razón, la ecuación de haz de Euler-Bernoulli se usa ampliamente en ingeniería , especialmente civil y mecánica, para determinar la resistencia (así como la desviación) de los haces en flexión.

Tanto el momento de flexión como la fuerza de corte causan tensiones en la viga. La tensión debida a la fuerza de corte es máxima a lo largo del eje neutro de la viga (cuando el ancho de la viga, t, es constante a lo largo de la sección transversal de la viga; de lo contrario, se debe evaluar la integral del primer momento y la anchura de la viga para la sección transversal particular), y la tensión de tracción máxima se encuentra en la superficie superior o inferior. Por lo tanto, la tensión principal máxima en la viga puede no estar en la superficie ni en el centro, sino en un área general. Sin embargo, las tensiones de fuerza de corte son despreciables en comparación con las tensiones de momento de flexión en todas las vigas excepto en la más compacta, así como el hecho de que las concentraciones de tensión comúnmente ocurren en las superficies, lo que significa que es probable que la tensión máxima en una viga esté en la superficie.

Flexión simple o simétrica [ editar ]

Elemento de una viga doblada: las fibras forman arcos concéntricos, las fibras superiores se comprimen y las fibras inferiores se estiran.

Para secciones transversales de haz que son simétricas alrededor de un plano perpendicular al plano neutro, se puede mostrar que la tensión de tracción experimentada por el haz puede expresarse como:

$${\ displaystyle \ sigma = {\ frac {Mz} {I}} = - zE ~ {\ frac {\ mathrm {d} ^ {2} w} {\ mathrm {d} x ^ {2}}}. \ ,}

Aquí, $${\ displaystyle z}es la distancia desde el eje neutro a un punto de interés; y$${\ displaystyle M}Es el momento de flexión. Tenga en cuenta que esta ecuación implica que la flexión pura(de signo positivo) causará tensión cero en el eje neutral, tensión positiva (tensión) en la "parte superior" de la viga y tensión negativa (compresión) en la parte inferior de la viga; y también implica que la tensión máxima estará en la superficie superior y la mínima en la parte inferior. Esta tensión de flexión puede superponerse con tensiones aplicadas axialmente, lo que provocará un cambio en el eje neutro (tensión cero).

Tensiones máximas en una sección transversal [ editar ]

Cantidades utilizadas en la definición del módulo de sección de una viga.

La tensión de tracción máxima en una sección transversal se encuentra en la ubicación $${\ displaystyle z = c_ {1}} y el esfuerzo de compresión máximo está en la ubicación $${\ displaystyle z = -c_ {2}} donde la altura de la sección transversal es $${\ displaystyle h = c_ {1} + c_ {2}}. Estas tensiones son

$${\ displaystyle \ sigma _ {1} = {\ cfrac {Mc_ {1}} {I}} = {\ cfrac {M} {S_ {1}}} ~; ~~ \ sigma _ {2} = - { \ cfrac {Mc_ {2}} {I}} = - {\ cfrac {M} {S_ {2}}}}

Las cantidades $${\ displaystyle S_ {1}, S_ {2}}son la sección moduli ^[5] y se definen como

$${\ displaystyle S_ {1} = {\ cfrac {I} {c_ {1}}} ~; ~~ S_ {2} = {\ cfrac {I} {c_ {2}}}}

El módulo de sección combina toda la información geométrica importante sobre la sección de una viga en una cantidad. En el caso de que una viga sea doblemente simétrica,$${\ displaystyle c_ {1} = c_ {2}} y tenemos un módulo de sección $${\ displaystyle S = I / c}.

Tensión en una viga de Euler-Bernoulli [ editar ]

Necesitamos una expresión para la tensión en términos de la desviación de la superficie neutra para relacionar las tensiones en un haz de Euler-Bernoulli con la desviación. Para obtener esa expresión utilizamos el supuesto de que las normales a la superficie neutra permanecen normales durante la deformación y que las desviaciones son pequeñas. Estas suposiciones implican que el haz se dobla en un arco de círculo de radio$${\ displaystyle \ rho}(ver Figura 1) y que la superficie neutra no cambia de longitud durante la deformación. ^[5]

Dejar $${\ displaystyle \ mathrm {d} x}ser la longitud de un elemento de la superficie neutra en el estado no deformado. Para pequeñas desviaciones, el elemento no cambia su longitud después de doblarse, sino que se deforma en un arco de círculo de radio$${\ displaystyle \ rho}. Si$${\ displaystyle \ mathrm {d} \ theta} Es el ángulo subtendido por este arco, entonces $${\ displaystyle \ mathrm {d} x = \ rho ~ \ mathrm {d} \ theta}.

Consideremos ahora otro segmento del elemento a distancia. $${\ displaystyle z}por encima de la superficie neutra. La longitud inicial de este elemento es$${\ displaystyle \ mathrm {d} x}. Sin embargo, después de doblar, la longitud del elemento se convierte en$${\ displaystyle \ mathrm {d} x '= (\ rho -z) ~ \ mathrm {d} \ theta = \ mathrm {d} xz ~ \ mathrm {d} \ theta}. La tensión en ese segmento de la viga está dada por

$${\ displaystyle \ varepsilon _ {x} = {\ cfrac {\ mathrm {d} x '- \ mathrm {d} x} {\ mathrm {d} x}} = - {\ cfrac {z} {\ rho} } = - \ kappa ~ z}

dónde $${\ displaystyle \ kappa}Es la curvatura de la viga. Esto nos da la tensión axial en la viga en función de la distancia desde la superficie neutra. Sin embargo, todavía necesitamos encontrar una relación entre el radio de curvatura y la desviación del haz.$${\ displaystyle w}.

Relación entre curvatura y deflexión del haz [ editar ]

Sea P un punto en la superficie neutra de la viga a una distancia $${\ displaystyle x} desde el origen de la $${\ displaystyle (x, z)}sistema coordinado. La pendiente de la viga es aproximadamente igual al ángulo formado por la superficie neutra con la$${\ displaystyle x}-axis para los pequeños ángulos encontrados en la teoría del haz. Por lo tanto, con esta aproximación,

$${\ displaystyle \ theta (x) = {\ cfrac {\ mathrm {d} w} {\ mathrm {d} x}}}

Por lo tanto, para un elemento infinitesimal. $${\ displaystyle \ mathrm {d} x}, la relación $${\ displaystyle \ mathrm {d} x = \ rho ~ \ mathrm {d} \ theta} Se puede escribir como

$${\ displaystyle {\ cfrac {1} {\ rho}} = {\ cfrac {\ mathrm {d} \ theta} {\ mathrm {d} x}} = {\ cfrac {\ mathrm {d} ^ {2} w} {\ mathrm {d} x ^ {2}}} = \ kappa}

Por lo tanto, la tensión en la viga se puede expresar como

$${\ displaystyle \ varepsilon _ {x} = - z \ kappa}

Las relaciones tensión-deformación [ editar ]

Para un material elástico lineal isotrópico homogéneo , la tensión está relacionada con la deformación por$${\ displaystyle \ sigma = E \ varepsilon}, dónde $${\ displaystyle E}es el módulo de los jóvenes . De ahí que la tensión en un haz de Euler-Bernoulli esté dada por

$${\ displaystyle \ sigma _ {x} = - zE {\ cfrac {\ mathrm {d} ^ {2} w} {\ mathrm {d} x ^ {2}}}}

Tenga en cuenta que la relación anterior, cuando se compara con la relación entre la tensión axial y el momento de flexión, conduce a

$${\ displaystyle M = -EI {\ cfrac {\ mathrm {d} ^ {2} w} {\ mathrm {d} x ^ {2}}}}

Dado que la fuerza de corte está dada por $${\ displaystyle Q = \ mathrm {d} M / \ mathrm {d} x}, también tenemos

$${\ displaystyle Q = -EI {\ cfrac {\ mathrm {d} ^ {3} w} {\ mathrm {d} x ^ {3}}}}

Consideraciones de límites [ editar ]

La ecuación de haz contiene una derivada de cuarto orden en $${\ displaystyle x}. Para encontrar una solución única.$${\ displaystyle w (x, t)}Necesitamos cuatro condiciones de contorno. Las condiciones de contorno generalmente son compatibles con elmodelo , pero también pueden modelar cargas puntuales, cargas distribuidas y momentos. Las condiciones de soporte o límite de desplazamiento se utilizan para fijar los valores de desplazamiento ($${\ displaystyle w}) y rotaciones ($${\ displaystyle \ mathrm {d} w / \ mathrm {d} x}) en el límite. Tales condiciones de frontera también se denominan condiciones de frontera de Dirichlet . Las condiciones de límite de carga y momento implican derivados más altos de$${\ displaystyle w}y representar el flujo de momento . Las condiciones de frontera de flujo también se denominan condiciones de frontera de Neumann .

Como ejemplo, considere una viga en voladizo que está incorporada en un extremo y libre en el otro como se muestra en la figura adyacente. En el extremo incorporado de la viga no puede haber ningún desplazamiento o rotación de la viga. Esto significa que en el extremo izquierdo, tanto la desviación como la pendiente son cero. Como no se aplica ningún momento de flexión externo en el extremo libre de la viga, el momento de flexión en esa ubicación es cero. Además, si no se aplica ninguna fuerza externa a la viga, la fuerza de corte en el extremo libre también es cero.

Tomando el $${\ displaystyle x} coordenada del extremo izquierdo como $${\ displaystyle 0} y el extremo derecho como $${\ displaystyle L} (la longitud de la viga), estas declaraciones se traducen al siguiente conjunto de condiciones de frontera (suponga que $${\ displaystyle EI} es una constante):

$${\ displaystyle w | _ {x = 0} = 0 \ quad; \ quad {\ frac {\ partial w} {\ partial x}} {\ bigg |} _ {x = 0} = 0 \ qquad {\ mbox {(extremo fijo)}} \,}

Una viga en voladizo.

$${\ displaystyle {\ frac {\ parcial ^ {2} w} {\ parcial x ^ {2}}} {\ bigg |} _ {x = L} = 0 \ quad; \ quad {\ frac {\ parcial ^ {3} w} {\ parcial x ^ {3}}} {\ bigg |} _ {x = L} = 0 \ qquad {\ mbox {(extremo libre)}} \,}

Un soporte simple (pin o rodillo) es equivalente a una fuerza puntual en la viga que se ajusta de tal manera que se fije la posición de la viga en ese punto. Un soporte fijo o abrazadera, es equivalente a la combinación de una fuerza puntual y un par de puntos que se ajusta de tal manera que se fije la posición y la pendiente de la viga en ese punto. Las fuerzas puntuales y los pares, ya sean de soportes o aplicados directamente, dividirán un haz en un conjunto de segmentos, entre los cuales la ecuación del haz producirá una solución continua, dadas cuatro condiciones de contorno, dos en cada extremo del segmento. Suponiendo que el producto EI es una constante, y definitoria$${\ displaystyle \ lambda = F / EI}donde F es la magnitud de una fuerza puntual, y$${\ displaystyle \ tau = M / EI}donde M es la magnitud de un punto de torsión, las condiciones de contorno apropiadas para algunos casos comunes se dan en la tabla a continuación. El cambio en un derivado particular de w a través del límite cuando x aumenta se denota por$${\ displaystyle \ Delta}seguido de ese derivado. Por ejemplo,$${\ displaystyle \ Delta w '' = w '' (x +) - w '' (x-)} dónde $${\ displaystyle w '' (x +)} es el valor de $${\ displaystyle w ''} en el límite inferior del segmento superior, mientras que $${\ displaystyle w '' (x-)} es el valor de $${\ displaystyle w ''}en el límite superior del segmento inferior. Cuando los valores de la derivada particular no solo son continuos a través del límite, sino que también se fijan, la condición del límite se escribe, por ejemplo,$${\ displaystyle \ Delta w '' = 0 ^ {*}} que en realidad constituye dos ecuaciones separadas (por ejemplo, $${\ displaystyle w '' (x -) = w '' (x +)} = fijo).

Límite	$${\ displaystyle w '' '}	$${\ displaystyle w ''}	$${\ displaystyle w '}	$${\ displaystyle w}
Abrazadera			$${\ displaystyle \ Delta w '= 0 ^ {*}}	$${\ displaystyle \ Delta w = 0 ^ {*}}
Soporte simple		$${\ displaystyle \ Delta w '' = 0}	$${\ displaystyle \ Delta w '= 0}	$${\ displaystyle \ Delta w = 0 ^ {*}}
Fuerza puntual	$${\ displaystyle \ Delta w '' '= \ lambda}	$${\ displaystyle \ Delta w '' = 0}	$${\ displaystyle \ Delta w '= 0}	$${\ displaystyle \ Delta w = 0}
Punto de torsión	$${\ displaystyle \ Delta w '' '= 0}	$${\ displaystyle \ Delta w '' = \ tau}	$${\ displaystyle \ Delta w '= 0}	$${\ displaystyle \ Delta w = 0}
Final libre	$${\ displaystyle w '' '= 0}	$${\ displaystyle w '' = 0}
Abrazadera en el extremo			$${\ displaystyle w '} fijo	$${\ displaystyle w} fijo
Fin simplemente apoyado		$${\ displaystyle w '' = 0}		$${\ displaystyle w} fijo
Punto de fuerza al final	$${\ displaystyle w '' '= \ pm \ lambda}	$${\ displaystyle w '' = 0}
Punto de torsión al final	$${\ displaystyle w '' '= 0}	$${\ displaystyle w '' = \ pm \ tau}

Tenga en cuenta que en los primeros casos, en los que las fuerzas puntuales y los pares se ubican entre dos segmentos, existen cuatro condiciones de contorno, dos para el segmento inferior y dos para el superior. Cuando se aplican fuerzas y pares de torsión a un extremo de la viga, se dan dos condiciones de contorno que se aplican en ese extremo. El signo de las fuerzas puntuales y los pares de torsión en un extremo será positivo para el extremo inferior, negativo para el extremo superior.

Consideraciones de carga [ editar ]

Las cargas aplicadas se pueden representar a través de condiciones de contorno o mediante la función $${\ displaystyle q (x, t)}que representa una carga distribuida externa. El uso de carga distribuida es a menudo favorable para la simplicidad. Sin embargo, las condiciones de contorno se utilizan a menudo para modelar cargas según el contexto; Esta práctica es especialmente común en el análisis de vibraciones.

Por naturaleza, la carga distribuida suele representarse de forma fragmentada, ya que en la práctica una carga no suele ser una función continua. Las cargas puntuales se pueden modelar con la ayuda de la función delta de Dirac . Por ejemplo, considere un haz de voladizo uniforme estático de longitud$${\ displaystyle L} con un punto de carga ascendente $${\ displaystyle F}Aplicado en el extremo libre. Usando condiciones de contorno, esto puede ser modelado de dos maneras. En el primer enfoque, la carga puntual aplicada se aproxima por una fuerza de corte aplicada en el extremo libre. En ese caso, la ecuación gobernante y las condiciones de contorno son:

{\ displaystyle {\ begin {alineado} & EI {\ frac {\ mathrm {d} ^ {4} w} {\ mathrm {d} x ^ {4}}} = 0 \\ & w | _ {x = 0} = 0 \ quad; \ quad {\ frac {\ mathrm {d} w} {\ mathrm {d} x}} {\ bigg |} _ {x = 0} = 0 \ quad; \ quad {\ frac {\ mathrm {d} ^ {2} w} {\ mathrm {d} x ^ {2}}} {\ bigg |} _ {x = L} = 0 \ quad; \ quad -EI {\ frac {\ mathrm { d} ^ {3} w} {\ mathrm {d} x ^ {3}}} {\ bigg |} _ {x = L} = F \, \ end {alineado}}}

Alternativamente, podemos representar la carga puntual como una distribución utilizando la función Dirac. En ese caso la ecuación y las condiciones de contorno son

{\ displaystyle {\ begin {alineado} & EI {\ frac {\ mathrm {d} ^ {4} w} {\ mathrm {d} x ^ {4}}} = F \ delta (xL) \\ & w | _ {x = 0} = 0 \ quad; \ quad {\ frac {\ mathrm {d} w} {\ mathrm {d} x}} {\ bigg |} _ {x = 0} = 0 \ quad; \ quad {\ frac {\ mathrm {d} ^ {2} w} {\ mathrm {d} x ^ {2}}} {\ bigg |} _ {x = L} = 0 \, \ end {alineado}}}

Tenga en cuenta que la condición de límite de fuerza de corte (tercera derivada) se elimina, de lo contrario habría una contradicción. Estos son problemas de valor de límite equivalentes , y ambos proporcionan la solución.

$${\ displaystyle w = {\ frac {F} {6EI}} (3Lx ^ {2} -x ^ {3}) \, ~.}

La aplicación de varias cargas puntuales en diferentes lugares llevará a $${\ displaystyle w (x)}siendo una función por partes. El uso de la función de Dirac simplifica enormemente tales situaciones; de lo contrario, la viga tendría que dividirse en secciones, cada una con cuatro condiciones de contorno resueltas por separado. Una familia de funciones bien organizada llamadas funciones Singularity se usan a menudo como una abreviatura para la función de Dirac, su derivado y sus antiderivadas .

Los fenómenos dinámicos también se pueden modelar utilizando la ecuación de haz estático mediante la elección de formas apropiadas de la distribución de carga. Como ejemplo, la vibración libre de una viga puede explicarse utilizando la función de carga:

$${\ displaystyle q (x, t) = \ mu {\ frac {\ partial ^ {2} w} {\ partial t ^ {2}}} \,}

dónde $${\ displaystyle \ mu}Es la densidad de masa lineal del haz, no necesariamente una constante. Con esta carga dependiente del tiempo, la ecuación del haz será una ecuación diferencial parcial :

$${\ displaystyle {\ frac {\ parcial ^ {2}} {\ parcial x ^ {2}}} \ izquierda (EI {\ frac {\ parcial ^ {2} w} {\ parcial x ^ {2}}} \ right) = - \ mu {\ frac {\ partial ^ {2} w} {\ partial t ^ {2}}}.}

Otro ejemplo interesante describe la deflexión de un haz que gira con una frecuencia angular constante de$${\ displaystyle \ omega}:

$${\ displaystyle q (x) = \ mu \ omega ^ {2} w (x) \,}

Esta es una distribución de fuerza centrípeta . Tenga en cuenta que en este caso,$${\ displaystyle q}es una función del desplazamiento (la variable dependiente), y la ecuación del haz será una ecuación diferencial ordinaria autónoma .

Ejemplos [ editar ]

Tres puntos de flexión [ editar ]

La prueba de flexión de tres puntos es un experimento clásico en mecánica. Representa el caso de una viga que descansa sobre dos soportes de rodillos y está sujeta a una carga concentrada aplicada en el centro de la viga. El corte es constante en valor absoluto: es la mitad de la carga central, P / 2. Cambia el signo en el centro de la viga. El momento de flexión varía linealmente desde un extremo, donde es 0, y el centro donde su valor absoluto es PL / 4, es donde el riesgo de ruptura es el más importante. La deformación de la viga se describe mediante un polinomio de tercer grado sobre una media viga (la otra mitad es simétrica). Los momentos de flexión ($${\ displaystyle M}), fuerzas de corte ($${\ displaystyle Q}), y deflexiones ($${\ displaystyle w}) para una viga sometida a una carga puntual central y una carga puntual asimétrica se dan en la tabla a continuación. ^[5]

Distribución	Max. valor
Viga simplemente soportada con carga central.
{\ displaystyle M (x) = {\ begin {cases} {\ frac {Px} {2}}, & {\ mbox {for}} 0 \ leq x \ leq {\ tfrac {L} {2}} \ \ {\ frac {P (Lx)} {2}}, & {\ mbox {for}} {\ tfrac {L} {2}}	$${\ displaystyle M_ {L / 2} = {\ tfrac {PL} {4}}}
{\ displaystyle Q (x) = {\ begin {cases} {\ frac {P} {2}}, & {\ mbox {for}} 0 \ leq x \ leq {\ tfrac {L} {2}} \ \ {\ frac {-P} {2}}, & {\ mbox {for}} {\ tfrac {L} {2}}	$${\ displaystyle | Q_ {0} | = | Q_ {L} | = {\ tfrac {P} {2}}}
{\ displaystyle w (x) = {\ begin {cases} - {\ frac {Px (4x ^ {2} -3L ^ {2})} {48EI}}, & {\ mbox {for}} 0 \ leq x \ leq {\ tfrac {L} {2}} \\ {\ frac {P (xL) (L ^ {2} -8Lx + 4x ^ {2})} {48EI}}, & {\ mbox {for }} {\ tfrac {L} {2}}	$${\ displaystyle w_ {L / 2} = {\ tfrac {PL ^ {3}} {48EI}}}
Viga simplemente soportada con carga asimétrica.
{\ displaystyle M (x) = {\ begin {cases} {\ tfrac {Pbx} {L}}, & {\ mbox {for}} 0 \ leq x \ leq a \\ {\ tfrac {Pbx} {L }} - P (xa) = {\ tfrac {Pa (Lx)} {L}}, & {\ mbox {para}} a	$${\ displaystyle M_ {B} = {\ tfrac {Pab} {L}}}
{\ displaystyle Q (x) = {\ begin {cases} {\ tfrac {Pb} {L}}, & {\ mbox {for}} 0 \ leq x \ leq a \\ {\ tfrac {Pb} {L }} - P, & {\ mbox {para}} a	$${\ displaystyle Q_ {A} = {\ tfrac {Pb} {L}}} $${\ displaystyle Q_ {C} = {\ tfrac {Pa} {L}}}
{\ displaystyle w (x) = {\ begin {cases} {\ tfrac {Pbx (L ^ {2} -b ^ {2} -x ^ {2})} {6LEI}}, & 0 \ leq x \ leq a \\ {\ tfrac {Pbx (L ^ {2} -b ^ {2} -x ^ {2})} {6LEI}} + {\ tfrac {P (xa) ^ {3}} {6EI}} , & a	$${\ displaystyle w _ {\ mathrm {max}} = {\ tfrac {{\ sqrt {3}} Pb (L ^ {2} -b ^ {2}) ^ {\ frac {3} {2}}} { 27LEI}}} a $${\ displaystyle x = {\ sqrt {\ tfrac {L ^ {2} -b ^ {2}} {3}}}}

Vigas en voladizo [ editar ]

Otra clase importante de problemas involucra vigas en voladizo . Los momentos de flexión ($${\ displaystyle M}), fuerzas de corte ($${\ displaystyle Q}), y deflexiones ($${\ displaystyle w}) para una viga en voladizo sujeta a una carga puntual en el extremo libre y una carga distribuida de manera uniforme en la tabla a continuación. ^[5]

Distribución	Max. valor
Viga voladiza con carga final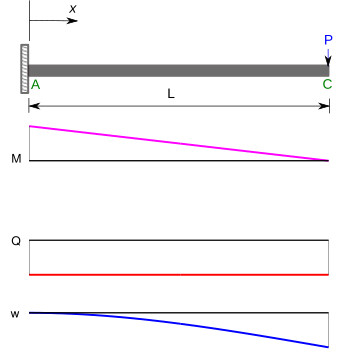
$${\ displaystyle M (x) = P (Lx)}	$${\ displaystyle M_ {A} = PL}
$${\ displaystyle Q (x) = P}	$${\ displaystyle Q _ {\ mathrm {max}} = P}
$${\ displaystyle w (x) = {\ tfrac {Px ^ {2} (3L-x)} {6EI}}}	$${\ displaystyle w_ {C} = {\ tfrac {PL ^ {3}} {3EI}}}
Viga voladiza con carga distribuida uniformemente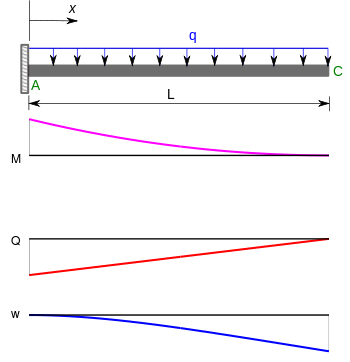
$${\ displaystyle M (x) = - {\ tfrac {q (L ^ {2} -2Lx + x ^ {2})} {2}}}	$${\ displaystyle M_ {A} = {\ tfrac {qL ^ {2}} {2}}}
$${\ displaystyle Q (x) = q (Lx),}	$${\ displaystyle Q_ {A} = qL}
$${\ displaystyle w (x) = {\ tfrac {qx ^ {2} (6L ^ {2} -4Lx + x ^ {2})} {24EI}}}	$${\ displaystyle w_ {C} = {\ tfrac {qL ^ {4}} {8EI}}}

Las soluciones para varias otras configuraciones comunes se encuentran fácilmente disponibles en libros de texto sobre mecánica de materiales y manuales de ingeniería.