ECUACIONES

ecuación de Ergun , derivada por el ingeniero químico turco Sabri Ergun en 1952, expresa el factor de fricción en una columna empaquetada en función del número de Reynolds modificado .

Ecuación [ editar ]

$${\ displaystyle f_ {p} = {\ frac {150} {Gr_ {p}}} + 1.75}

dónde $${\ displaystyle f_ {p}} y $${\ displaystyle Gr_ {p}} se definen como

$${\ displaystyle f_ {p} = {\ frac {\ Delta p} {L}} {\ frac {D_ {p}} {\ rho v_ {s} ^ {2}}} \ left ({\ frac {\ epsilon ^ {3}} {1- \ epsilon}} \ right)} y $${\ displaystyle Gr_ {p} = {\ frac {\ rho v_ {s} D_ {p}} {(1- \ epsilon) \ mu}}}

dónde: $${\ displaystyle Gr_ {p}} es el número de Reynolds modificado,

fp es el factor de fricción del lecho empacado
$${\ displaystyle \ Delta p} es la caída de presión a través de la cama,
$${\ displaystyle L} es la longitud de la cama (no la columna),
$${\ displaystyle D_ {p}} es el diámetro esférico equivalente del embalaje,
$${\ displaystyle \ rho}es la densidad del fluido,
$${\ displaystyle \ mu}Es la viscosidad dinámica del fluido.
$${\ displaystyle v_ {s}}es la velocidad superficial (es decir, la velocidad que tendría el fluido a través del tubo vacío a la misma tasa de flujo volumétrico), y
$${\ displaystyle \ epsilon}es la fracción vacía de la cama ( porosidad de la cama en cualquier momento).

Extensión [ editar ]

La extensión de la ecuación de Ergun a los lechos fluidizados es discutida por Akgiray y Saatçı (2001). Para calcular la caída de presión en un reactor dado, se puede deducir la siguiente ecuación

$${\ displaystyle \ Delta p = {\ frac {150 \ mu ~ L} {D_ {p} ^ {2}}} ~ {\ frac {(1- \ epsilon) ^ {2}} {\ epsilon ^ {3 }}} v_ {s} + {\ frac {1.75 ~ L ~ \ rho} {D_ {p}}} ~ {\ frac {(1- \ epsilon)} {\ epsilon ^ {3}}} v_ {s } | v_ {s} |}

Esta disposición de la ecuación de Ergun deja clara su estrecha relación con la ecuación más simple de Kozeny-Carman que describe el flujo laminar de fluidos a través de lechos empacados.

La teoría del haz de Euler-Bernoulli (también conocida como teoría del haz del ingeniero o teoría del haz clásica ) ^[1] es una simplificación de la teoría lineal de la elasticidadque proporciona un medio para calcular las características de carga y deflexión de los haces . Cubre el estuche para pequeñas desviaciones de una viga que están sujetas únicamente a cargas laterales. Es, pues, un caso especial de la teoría del haz de Timoshenko . Fue enunciado por primera vez alrededor de 1750, ^[2] pero no se aplicó a gran escala hasta el desarrollo de la Torre Eiffel y la noria.A finales del siglo XIX. Tras estas exitosas demostraciones, rápidamente se convirtió en la piedra angular de la ingeniería y en un habilitador de la Segunda Revolución Industrial .

Se han desarrollado herramientas de análisis adicionales, como la teoría de placas y el análisis de elementos finitos , pero la simplicidad de la teoría del haz la convierte en una herramienta importante en las ciencias, especialmente en ingeniería estructural y mecánica .

Historia [ editar ]

Esquema de la sección transversal de una viga curvada que muestra el eje neutro.

El consenso predominante es que Galileo Galileihizo los primeros intentos de desarrollar una teoría de vigas, pero estudios recientes argumentan que Leonardo da Vinci fue el primero en hacer las observaciones cruciales. Da Vinci carecía de la ley y el cálculo de Hooke para completar la teoría, mientras que Galileo fue retenido por una suposición incorrecta que hizo. ^[3]

La viga de Bernoulli lleva el nombre de Jacob Bernoulli , quien hizo los descubrimientos significativos. Leonhard Euler y Daniel Bernoullifueron los primeros en armar una teoría útil alrededor de 1750. ^[4] En ese momento, la ciencia y la ingeniería eran vistos como campos muy distintos, y existía una duda considerable de que se podía confiar en un producto matemático del mundo académico. Prácticas aplicaciones de seguridad. Los puentes y edificios continuaron siendo diseñados por precedentes hasta fines del siglo XIX, cuando la Torre Eiffel y la Noria demostraron la validez de la teoría en grandes escalas.

Ecuación haz estático [ editar ]

La ecuación de Euler-Bernoulli describe la relación entre la desviación de la viga y la carga aplicada: ^[5]

$${\ displaystyle {\ frac {\ mathrm {d} ^ {2}} {\ mathrm {d} x ^ {2}}} \ left (EI {\ frac {\ mathrm {d} ^ {2} w} { \ mathrm {d} x ^ {2}}} \ right) = q \,}

La curva $${\ displaystyle w (x)} describe la desviación de la viga en el $${\ displaystyle z} dirección en alguna posición $${\ displaystyle x} (recuerde que la viga se modela como un objeto unidimensional). $${\ displaystyle q}es una carga distribuida, en otras palabras, una fuerza por unidad de longitud (análoga a la presión que es una fuerza por área); puede ser una función de$${\ displaystyle x}, $${\ displaystyle w}, u otras variables. $${\ displaystyle E}es el módulo elástico y$${\ displaystyle I}Es el segundo momento de área de la sección transversal de la viga.$${\ displaystyle I}debe calcularse con respecto al eje que pasa por el centroide de la sección transversal y que es perpendicular a la carga aplicada. ^{[N 1]} Explícitamente, para una viga cuyo eje está orientado a lo largo de x con una carga a lo largo de z , la sección transversal de la viga está en el plano yz , y el segundo momento relevante del área es

$${\ displaystyle I = \ iint z ^ {2} \; dy \; dz,}

donde se supone que el centroide de la sección transversal ocurre en y  = z  = 0.

A menudo, el producto EI (conocido como la rigidez a la flexión ) es una constante, por lo que

$${\ displaystyle EI {\ frac {\ mathrm {d} ^ {4} w} {\ mathrm {d} x ^ {4}}} = q (x). \,}

Esta ecuación, que describe la desviación de un haz estático y uniforme, se usa ampliamente en la práctica de la ingeniería. Expresiones tabuladas para la deflexión.$${\ displaystyle w}Para configuraciones de vigas comunes se pueden encontrar en manuales de ingeniería. Para situaciones más complicadas, la desviación se puede determinar resolviendo la ecuación de Euler-Bernoulli usando técnicas como el " método de desviación de pendiente ", el " método de distribución de momento ", el " método de área de momento , el" método de haz conjugado "," el principio de trabajo virtual "," integración directa "," método de Castigliano "," método de Macaulay "o el" método de rigidez directa ".

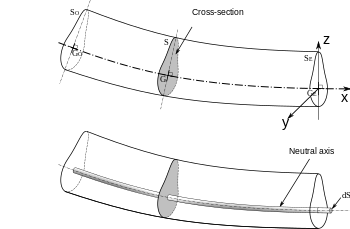
Las convenciones de signos se definen aquí, ya que se pueden encontrar diferentes convenciones en la literatura. ^[5] En este artículo, se utiliza un sistema de coordenadas para diestros como se muestra en la figura, Curva de una viga de Euler-Bernoulli. En esta figura, se muestran las direcciones x y z de un sistema de coordenadas para diestros. Ya que$${\ displaystyle \ mathbf {e_ {z}} \ times \ mathbf {e_ {x}} = \ mathbf {e_ {y}}} dónde $${\ displaystyle \ mathbf {e_ {x}}}, $${\ displaystyle \ mathbf {e_ {y}}}y $${\ displaystyle \ mathbf {e_ {z}}}son vectores unitarios en la dirección de los ejes x, y y z, respectivamente, la dirección del eje y está en la figura. Fuerzas actuando en lo positivo.$${\ displaystyle x} y $${\ displaystyle z}Las direcciones se asumen positivas. El signo del momento de flexión.$${\ displaystyle M} es positivo cuando el vector de par asociado con el momento de flexión en el lado derecho de la sección está en la dirección y positiva (es decir, para que un valor positivo de $${\ displaystyle M}conduce a una tensión de compresión en las fibras del fondo). Con esta elección de convención de signo de momento de flexión, para tener$${\ displaystyle dM = Qdx}, Es necesario que $${\ displaystyle Q}la fuerza de corte que actúa en el lado derecho de la sección será positiva en la dirección z para lograr el equilibrio estático de los momentos. Tener fuerza de equilibrio con$${\ displaystyle dQ = qdx}, q, la intensidad de carga debe ser positiva en la dirección z menos. Además de estas convenciones de signos para cantidades escalares, a veces también usamos vectores en los que las direcciones de los vectores se aclaran mediante el uso de los vectores unitarios.$${\ displaystyle \ mathbf {e_ {x}}}, $${\ displaystyle \ mathbf {e_ {y}}}y $${\ displaystyle \ mathbf {e_ {z}}}.

Las derivadas sucesivas de la deflexión w tienen significados físicos importantes: d w / d x es la pendiente de la viga,

$${\ displaystyle M = -EI {\ frac {d ^ {2} w} {dx ^ {2}}}}

es el momento de flexión en la viga, y

$${\ displaystyle Q = - {\ frac {d} {dx}} \ left (EI {\ frac {d ^ {2} w} {dx ^ {2}}} \ right)}

Es la fuerza de corte en la viga.

Doblado de una viga de Euler-Bernoulli. Cada sección transversal de la viga está a 90 grados con respecto al eje neutral.

Las tensiones en una viga pueden calcularse a partir de las expresiones anteriores después de que se haya determinado la desviación debida a una carga dada.

Derivación de la ecuación del momento de flexión [ editar ]

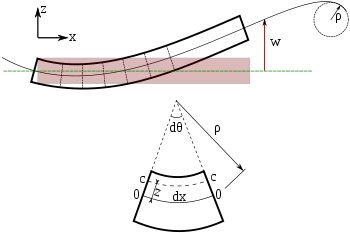
Debido a la importancia fundamental de la ecuación del momento de flexión en la ingeniería, proporcionaremos una breve derivación. Cambiamos a coordenadas polares. La longitud del eje neutro en la figura es$${\ displaystyle \ rho d \ theta.} La longitud de una fibra con una distancia radial. $${\ displaystyle z} debajo del eje neutro es $${\ displaystyle (\ rho + z) d \ theta.} Por lo tanto, la tensión de esta fibra es

$${\ displaystyle {\ frac {\ left (\ rho + z- \ rho \ right) \ d \ theta} {\ rho \ d \ theta}} = {\ frac {z} {\ rho}}.}

El estrés de esta fibra es $${\ displaystyle E {\ tfrac {z} {\ rho}}}donde E es el módulo elástico de acuerdo con la Ley de Hooke . El vector de fuerza diferencial,$${\ displaystyle d \ mathbf {F},} El resultado de este estrés está dado por,

$${\ displaystyle d \ mathbf {F} = E {\ frac {z} {\ rho}} dA \ mathbf {e_ {x}}.}

Este es el vector de fuerza diferencial ejercido en el lado derecho de la sección que se muestra en la figura. Sabemos que está en el$${\ displaystyle \ mathbf {e_ {x}}} dirección ya que la figura muestra claramente que las fibras en la mitad inferior están en tensión. $${\ displaystyle dA}Es el elemento diferencial de área en la ubicación de la fibra. El vector de momento de flexión diferencial,$${\ displaystyle d \ mathbf {M}} asociado con $${\ displaystyle d \ mathbf {F}} es dado por

$${\ displaystyle d \ mathbf {M} = -z \ mathbf {e_ {z}} \ times d \ mathbf {F} = - \ mathbf {e_ {y}} E {\ frac {z ^ {2}} { \ rho}} dA.}

Esta expresión es válida para las fibras en la mitad inferior de la viga. La expresión para las fibras en la mitad superior del haz será similar, excepto que el vector del brazo del momento estará en la dirección z positiva y el vector de la fuerza estará en la dirección -x ya que las fibras superiores están en compresión. Pero el vector del momento de flexión resultante seguirá en la dirección -y desde$${\ displaystyle \ mathbf {e_ {z}} \ times - \ mathbf {e_ {x}} = - \ mathbf {e_ {y}}.} Por lo tanto, nos integramos en toda la sección transversal de la viga y obtenemos para $${\ displaystyle \ mathbf {M}} el vector de momento de flexión ejercido en la sección transversal derecha de la viga la expresión

$${\ displaystyle \ mathbf {M} = \ int d \ mathbf {M} = - \ mathbf {e_ {y}} {\ frac {E} {\ rho}} \ int {z ^ {2}} \ dA = - \ mathbf {e_ {y}} {\ frac {EI} {\ rho}},}

dónde $${\ displaystyle I}Es el segundo momento de área . Del cálculo, sabemos que cuando$${\ displaystyle {\ tfrac {dw} {dx}}} es pequeño como lo es para una viga de Euler-Bernoulli, $${\ displaystyle {\ tfrac {1} {\ rho}} = {\ tfrac {d ^ {2} w} {dx ^ {2}}}} ($${\ displaystyle \ rho}es el radio de curvatura ). Por lo tanto,

$${\ displaystyle \ mathbf {M} = - \ mathbf {e_ {y}} EI {d ^ {2} w \ over dx ^ {2}}}

Ecuación de haz dinámico [ editar ]

Modelo de método de elementos finitos de una vibración de una viga de ala ancha (viga en I).

La ecuación de haz dinámico es la ecuación de Euler-Lagrange para la siguiente acción

$${\ displaystyle S = \ int _ {t_ {1}} ^ {t_ {2}} \ int _ {0} ^ {L} \ left [{\ frac {1} {2}} \ mu \ left ({ \ frac {\ parcial w} {\ parcial t}} \ derecha) ^ {2} - {\ frac {1} {2}} EI \ izquierda ({\ frac {\ parcial ^ {2} w} {\ parcial x ^ {2}}} \ right) ^ {2} + q (x) w (x, t) \ right] dxdt.}

El primer término representa la energía cinética donde $${\ displaystyle \ mu}es la masa por unidad de longitud; el segundo representa la energía potencial debido a fuerzas internas (cuando se considera con un signo negativo) y el tercer término representa la energía potencial debido a la carga externa$${\ displaystyle q (x)}. La ecuación de Euler-Lagrange se utiliza para determinar la función que minimiza la funcionalidad$${\ displaystyle S}. Para un haz dinámico de Euler-Bernoulli, la ecuación de Euler-Lagrange es

$${\ displaystyle {\ cfrac {\ partial ^ {2}} {\ partial x ^ {2}}} \ left (EI {\ cfrac {\ partial ^ {2} w} {\ partial x ^ {2}}} \ right) = - \ mu {\ cfrac {\ partial ^ {2} w} {\ partial t ^ {2}}} + q (x)}

MostrarDerivación de la ecuación de Euler-Lagrange para vigas

Cuando la viga es homogénea, $${\ displaystyle E} y $${\ displaystyle I} son independientes de $${\ displaystyle x}, y la ecuación del haz es más simple:

$${\ displaystyle EI {\ cfrac {\ parcial ^ {4} w} {\ parcial x ^ {4}}} = - \ mu {\ cfrac {\ parcial ^ {2} w} {\ parcial t ^ {2} }} + q \ ,.}

Vibración libre [ editar ]

En ausencia de una carga transversal, $${\ displaystyle q}, tenemos la ecuación de vibración libre . Esta ecuación se puede resolver utilizando una descomposición de Fourier del desplazamiento en la suma de las vibraciones armónicas de la forma.

$${\ displaystyle w (x, t) = {\ text {Re}} [{\ hat {w}} (x) ~ e ^ {- i \ omega t}]}

dónde $${\ displaystyle \ omega}Es la frecuencia de vibración. Entonces, para cada valor de frecuencia, podemos resolver una ecuación diferencial ordinaria

$${\ displaystyle EI ~ {\ cfrac {\ mathrm {d} ^ {4} {\ hat {w}}} {\ mathrm {d} x ^ {4}}} + \ mu \ omega ^ {2} {\ sombrero {w}} = 0 \ ,.}

La solución general de la ecuación anterior es

$${\ displaystyle {\ hat {w}} = A_ {1} \ cosh (\ beta x) + A_ {2} \ sinh (\ beta x) + A_ {3} \ cos (\ beta x) + A_ {4 } \ sin (\ beta x) \ quad {\ text {with}} \ quad \ beta: = \ left ({\ frac {\ mu \ omega ^ {2}} {EI}} \ right) ^ {1 / 4}}

dónde $${\ displaystyle A_ {1}, A_ {2}, A_ {3}, A_ {4}}son constantes Estas constantes son únicas para un conjunto dado de condiciones de contorno. Sin embargo, la solución para el desplazamiento no es única y depende de la frecuencia. Estas soluciones se escriben típicamente como

$${\ displaystyle {\ hat {w}} _ {n} = A_ {1} \ cosh (\ beta _ {n} x) + A_ {2} \ sinh (\ beta _ {n} x) + A_ {3 } \ cos (\ beta _ {n} x) + A_ {4} \ sin (\ beta _ {n} x) \ quad {\ text {with}} \ quad \ beta _ {n}: = \ left ( {\ frac {\ mu \ omega _ {n} ^ {2}} {EI}} \ right) ^ {1/4} \ ,.}

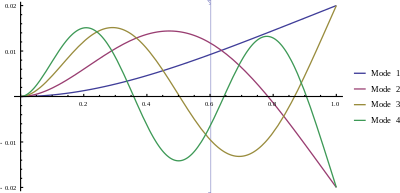
Las cantidades $${\ displaystyle \ omega _ {n}}Se llaman las frecuencias naturales del haz. Cada una de las soluciones de desplazamiento se denomina modo y la forma de la curva de desplazamiento se denomina forma de modo .

Ejemplo: viga en voladizo [ editar ]

Formas de modo para los primeros cuatro modos de una viga en voladizo vibrante.

Las condiciones de contorno para una viga de longitud en voladizo. $${\ displaystyle L} (fijado en $${\ displaystyle x = 0}) son

{\ displaystyle {\ begin {alineado} & {\ hat {w}} _ {n} = 0 ~, ~~ {\ frac {d {\ hat {w}} _ {n}} {dx}} = 0 \ quad {\ text {at}} ~~ x = 0 \\ & {\ frac {d ^ {2} {\ hat {w}} _ {n}} {dx ^ {2}}} = 0 ~, ~~ {\ frac {d ^ {3} {\ hat {w}} _ {n}} {dx ^ {3}}} = 0 \ quad {\ text {at}} ~~ x = L \ ,. \ end {alineado}}}

Si aplicamos estas condiciones, se encontrarán soluciones no triviales solo si $${\ displaystyle \ cosh (\ beta _ {n} L) \, \ cos (\ beta _ {n} L) + 1 = 0 \ ,.}Esta ecuación no lineal se puede resolver numéricamente. Las primeras raíces son β ₁ L / π = 0.59686 ..., β ₂ L / π = 1.49418 ..., β ₃ L / π = 2.50025 ..., β ₄ L / π = 3.49999 ...,. ..

Las correspondientes frecuencias naturales de vibración son:

$${\ displaystyle \ omega _ {1} = \ beta _ {1} ^ {2} {\ sqrt {\ frac {EI} {\ mu}}} = {\ frac {3.5161} {L ^ {2}}} {\ sqrt {\ frac {EI} {\ mu}}} ~, ~~ \ dots}

Las condiciones de contorno también se pueden usar para determinar las formas de modo de la solución para el desplazamiento:

$${\ displaystyle {\ hat {w}} _ {n} = A_ {1} {\ Bigl [} (\ cosh \ beta _ {n} x- \ cos \ beta _ {n} x) + {\ frac { \ cos \ beta _ {n} L + \ cosh \ beta _ {n} L} {\ sin \ beta _ {n} L + \ sinh \ beta _ {n} L}} (\ sin \ beta _ {n} x - \ sinh \ beta _ {n} x) {\ Bigr]}}

La constante desconocida (en realidad constantes como hay una para cada $${\ displaystyle n}) $${\ displaystyle A_ {1}}, que en general es complejo, está determinado por las condiciones iniciales en $${\ displaystyle t = 0}Sobre la velocidad y desplazamientos de la viga. Típicamente un valor de$${\ displaystyle A_ {1} = 1}Se utiliza al trazar formas de modo. Las soluciones al problema forzado no amortiguado tienen desplazamientos ilimitados cuando la frecuencia de conducción coincide con una frecuencia natural$${\ displaystyle \ omega _ {n}}, es decir, el haz puede resonar . Las frecuencias naturales de un haz corresponden, por lo tanto, a las frecuencias en las que puede ocurrir la resonancia .

Ejemplo: haz no admitido (libre-gratis) [ editar ]

Los primeros cuatro modos de una viga de Euler-Bernoulli libre de vibración libre.

Una viga libre es una viga sin soporte. ^[6]Las condiciones de contorno para un haz libre de longitud L que se extiende desde x= 0 a x = L viene dada por:

$${\ displaystyle {\ frac {d ^ {2} {\ hat {w}} _ {n}} {dx ^ {2}}} = 0 ~, ~~ {\ frac {d ^ {3} {\ hat {w}} _ {n}} {dx ^ {3}}} = 0 \ quad {\ text {at}} ~~ x = 0 \, {\ text {y}} \, L \ ,.}

Si aplicamos estas condiciones, se encontrarán soluciones no triviales solo si $${\ displaystyle \ cosh (\ beta _ {n} L) \, \ cos (\ beta _ {n} L) -1 = 0 \ ,.}

Esta ecuación no lineal se puede resolver numéricamente. Las primeras raíces son β ₁ L / π = 1.50562 ..., β ₂ L / π = 2.49975 ..., β ₃ L / π = 3.50001 ..., β ₄ L / π = 4.50000 ...

Las correspondientes frecuencias naturales de vibración son:

$${\ displaystyle \ omega _ {1} = \ beta _ {1} ^ {2} {\ sqrt {\ frac {EI} {\ mu}}} = {\ frac {22.3733} {L ^ {2}}} {\ sqrt {\ frac {EI} {\ mu}}} ~, ~~ \ dots}

Las condiciones de contorno también se pueden usar para determinar las formas de modo de la solución para el desplazamiento:

$${\ displaystyle {\ hat {w}} _ {n} = A_ {1} {\ Bigl [} (\ sin \ beta _ {n} x + \ sinh \ beta _ {n} x) + {\ frac {\ sin \ beta _ {n} L- \ sinh \ beta _ {n} L} {\ cosh \ beta _ {n} L- \ cos \ beta _ {n} L}} (\ cos \ beta _ {n} x + \ cosh \ beta _ {n} x) {\ Bigr]}}

Al igual que con el haz en voladizo, las constantes desconocidas están determinadas por las condiciones iniciales en $${\ displaystyle t = 0}Sobre la velocidad y desplazamientos de la viga. Además, las soluciones al problema forzado no amortiguado tienen desplazamientos ilimitados cuando la frecuencia de conducción coincide con una frecuencia natural$${\ displaystyle \ omega _ {n}}.