ECUACIONES

ecuación de Blaney-Criddle (llamada así por HF Blaney y WD Criddle) es un método para estimar la evapotranspiración del cultivo de referencia .

Uso [ editar ]

La ecuación de Blaney-Criddle es un método relativamente simplista para calcular la evapotranspiración . Cuando hay suficientes datos meteorológicos disponibles, generalmente se prefiere la ecuación de Penman-Monteith . Sin embargo, la ecuación de Blaney-Criddle es ideal cuando solo hay conjuntos de datos de temperatura del aire disponibles para un sitio.

Dada la precisión aproximada de la ecuación de Blaney-Criddle, se recomienda que se use para calcular la evapotranspiración por períodos de un mes o más [1] .

La ecuación calcula la evapotranspiración para un "cultivo de referencia", que se toma como un pasto verde en crecimiento activo de 8 a 15 cm de altura [2] .

Ecuación [ editar ]

ET _o = p · (0.457 · T _significa + 8.128)

Dónde:

ET _o es la evapotranspiración de referencia [mm día ⁻¹ ] (mensual)

T _media es la temperatura media diaria [° C] dada como T _media = (T _max + T _min ) / 2

p es el porcentaje medio diario de horas diurnas anuales. ^[1]

La precisión y sesgo [ editar ]

Dada la limitada entrada de datos a la ecuación, la evapotranspiración calculada debe considerarse como ampliamente precisa. En lugar de una medida precisa de la evapotranspiración , se considera mejor que la salida de la ecuación proporciona un orden de magnitud [3]

La inexactitud de la ecuación se ve agravada por variantes extremas del clima. En particular, se sabe que la evapotranspiración se exagera hasta en un 40% en áreas tranquilas, húmedas y nubladas y se deprecia en un 60% en áreas ventosas, secas y soleadas [4] .

Los rompecabezas de tablero con álgebra de variables binarias piden a los jugadores que ubiquen los objetos ocultos basándose en un conjunto de celdas de pista y sus vecinos marcados como variables (incógnitas). Una variable con valor de 1 corresponde a una celda con un objeto. Por el contrario, una variable con valor de 0 corresponde a una celda vacía, sin objeto oculto.

Descripción general [ editar ]

Estos rompecabezas se basan en el álgebra con variables binarias que toman un par de valores, por ejemplo, (no, sí), (falso, verdadero), (no existe, existe), ( 0 ,  1 ). Invita al jugador a establecer rápidamente algunas ecuaciones, y desigualdades para la solución. La partición se puede utilizar para reducir la complejidad del problema. Además, si el rompecabezas está preparado de manera que solo exista una solución única , este hecho se puede utilizar para eliminar algunas variables sin cálculo.

El problema se puede modelar como programación lineal de enteros binarios, que es un caso especial de programación lineal de enteros. ^[1]

Historia [ editar ]

Buscaminas , junto con sus variantes , es el ejemplo más notable de este tipo de rompecabezas.

Álgebra con variables binarias [ editar ]

Debajo de las letras en las declaraciones matemáticas se usan como variables donde cada una puede tomar el valor 0 o 1 solamente. A continuación se presenta un ejemplo simple de una ecuación con variables binarias:

a + b = 0

Aquí hay dos variables a y b, pero una ecuación. La solución está limitada por el hecho de que a y b solo pueden tomar los valores 0 o 1 . Aquí solo hay una solución, tanto a = 0 como b = 0 . Otro ejemplo simple se da a continuación:

a + b = 2

La solución es sencilla: a y b deben ser 1 para que a + b sea igual a 2 .

Otro caso interesante se muestra a continuación:

a + b + c = 2

a + b ≤ 1

Aquí, la primera declaración es una ecuación y la segunda declaración es una desigualdad que indica los tres casos posibles:

1. a = 1 y b = 0 ,
2. a = 0 y b = 1 , y
3. a = 0 y b = 0 ,

El último caso provoca una contradicción en c forzando c = 2 , lo cual no es posible. Por lo tanto, el primer o segundo caso es correcto. Esto lleva al hecho de que c debe ser 1 .

La modificación de una gran ecuación en una forma más pequeña no es difícil. Sin embargo, un conjunto de ecuaciones con variables binarias no se puede resolver siempre aplicando el álgebra lineal. El siguiente es un ejemplo para aplicar la resta de dos ecuaciones:

a + b + c + d = 3

c + d = 1

La primera declaración tiene cuatro variables, mientras que la segunda tiene solo dos variables. Este último significa que la suma de c y d es 1 . Usando este hecho en la primera declaración, las ecuaciones anteriores se pueden reducir a

a + b = 2

c + d = 1

El álgebra en un tablero [ editar ]

Figura 1: Un ejemplo de rompecabezas en un tablero 4x4.

Un juego basado en el álgebra con variables binarias se puede visualizar de muchas maneras diferentes. Una forma genérica es representar el lado derecho de una ecuación como una pista en una celda (celda de pista), y los vecinos de una celda de pista como variables. En la Figura 1 se muestra un caso simple. Se puede suponer que los vecinos son las celdas arriba / abajo, izquierda / derecha y esquina que comparten un borde o una esquina. Las celdas blancas pueden contener un objeto oculto o nada. En otras palabras, son las variables binarias. Tienen lugar en el lado izquierdo de las ecuaciones. Cada celda de pista, una celda con fondo azul en la Figura 1, contiene un número positivo correspondiente al número de sus vecinos que tienen objetos ocultos. El número total de objetos en el tablero se puede dar como una pista adicional. La misma tabla con las variables marcadas se muestra en la Figura 2.

La reducción en un conjunto de ecuaciones con variables binarias [ editar ]

La ecuación principal se escribe utilizando el número total de los objetos ocultos dados. Desde la primera figura esto corresponde a la siguiente ecuación.

a + b + c + d + e + f + g + h + i + j + k + m = 3

Las otras ecuaciones se componen una por una para cada celda de pista:

a + b + c + e + f + h + i + j = 1

f + g + j + m = 1

h + i + j + k = 2

i + j + m = 2

Aunque hay varias formas de resolver las ecuaciones anteriores, se puede aplicar la siguiente manera explícita:

1. Del conjunto de ecuaciones se sabe que i + j + m = 2 . Sin embargo, como j y m son vecinos de una celda con el número 1 , se cumple lo siguiente: j + m ≤ 1 . Esto significa que la variable i debe ser 1 .
2. Como i = 1 y la variable i es el vecino de la celda de pista con el número 1 , las variables a , b , c , e , f , hy j deben ser cero. El mismo resultado se puede obtener al reemplazar i = 1 en la segunda ecuación de la siguiente manera: a + b + c + e + f + h + j = 0 . Esto es equivalente a a = 0 , b = 0, c = 0 , e = 0 , f = 0 , h= 0 , j = 0 .
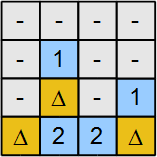
3. La Figura 3 se obtiene después del Paso 1 y el Paso 2. Las celdas en gris con '-' son las variables con valor 0 . La celda con el símbolo Δ corresponde a la variable con valor 1 . La variable k es el único vecino de la celda de la pista más a la izquierda con valor 2 . Esta celda de pista tiene un vecino con un objeto y solo una celda restante con la variable k . Por lo tanto, k debe ser 1 .
4. De manera similar, la variable m también debe ser 1 porque es la única variable que queda junto a la celda de la mayoría de las pistas con valor 2 .
5. Desde k = 1 , m = 1 y i = 1 , completamos el marcado de los tres objetos ocultos por lo tanto d = 0 , y g = 0 . La solución final se da en la Figura 4.

Figura 2: las variables binarias están marcadas

Figura 3: El ejemplo resuelto parcialmente.

Figura 4: El ejemplo resuelto.

Uso de la singularidad [ editar ]

En el ejemplo anterior (Figura 2), las variables a , b , c y e son las vecinas de la celda de la pista 1 y no son vecinas de ninguna otra celda. Es obvio que los siguientes son posibles soluciones:

• a = 1 , b = 0 , c = 0 , e = 0
• a = 0 , b = 1 , c = 0 , e = 0
• a = 0 , b = 0 , c = 1 , e = 0
• a = 0 , b = 0 , c = 0 , e = 1

Sin embargo, si el rompecabezas está preparado para que tengamos una única solución (única), podemos establecer que todas estas variables a , b , c y e deben ser 0. De lo contrario, habrá más de una solución.

Uso de la partición [ editar ]

Figura 5: Un ejemplo para particionar

Algunas configuraciones de rompecabezas pueden permitir que el jugador use la partición ^[2]Para la reducción de la complejidad. En la Figura 5 se muestra un ejemplo. Cada partición corresponde a un número de los objetos ocultos. La suma de los objetos ocultos en las particiones debe ser igual al número total de objetos ocultos en el tablero. Una forma posible de determinar una partición es elegir las celdas de pista principal que no tienen vecinos comunes. Las celdas fuera de las zonas transparentes rojas en la Figura 5 deben estar vacías. En otras palabras, no hay objetos ocultos en las celdas completamente blancas. Como debe haber un objeto oculto dentro de la zona de partición superior, la tercera fila desde arriba no debe contener un objeto oculto. Esto lleva al hecho de que las dos celdas variables en la fila inferior alrededor de la celda de la pista deben tener objetos ocultos. El resto de la solución es sencillo.

Uso del método de prueba y verificación [ editar ]

Figura 6: Un ejemplo para el método de probar y verificar

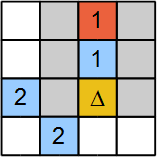
En algunos casos, el jugador puede establecer una celda variable como 1 y verificar si ocurre alguna inconsistencia. El ejemplo de la Figura 6 muestra una comprobación de inconsistencia. La celda marcada con un objeto oculto Δ está bajo prueba. Su marcación lleva al conjunto a que todas las variables (celdas en gris) sean 0 . Esto sigue a la inconsistencia. La celda de pista marcada en rojo con el valor 1 no tiene ningún vecino restante que pueda incluir un objeto oculto. Por lo tanto, la celda bajo la prueba no debe incluir un objeto oculto. En forma algebraica tenemos dos ecuaciones:

a + b + c + d = 1

a + b + c + d + e + f + g = 1

Aquí a , b , c , y d corresponden a las cuatro celdas grises superiores de la Figura 6. La celda con Δ está representada por la variable f , y las otras dos celdas en gris están marcadas como e y g . Si configuramos f = 1 , entonces a = 0 , b = 0 , c = 0 , d = 0 , e = 0 , g = 0 . La primera ecuación anterior tendrá el lado izquierdo igual a 0 mientras que el lado derecho tiene1 . Una contradicción.

Es posible que se deba aplicar el método de probar y verificar, en consecuencia, en más de un paso en algunos rompecabezas para llegar a una conclusión. Esto es equivalente al algoritmo de búsqueda binario ^[3] para eliminar posibles rutas que conducen a una inconsistencia.

Complejidad [ editar ]

Debido a las variables binarias, la ecuación establecida para la solución no posee propiedad de linealidad. En otras palabras, el rango de la matriz de ecuaciones no siempre aborda la complejidad correcta.

La complejidad de esta clase de rompecabezas se puede ajustar de varias maneras. Uno de los métodos más sencillos es establecer una proporción entre el número de celdas claves y el número total de celdas en el tablero. Sin embargo, esto puede resultar en un rango de complejidad muy variable para una proporción fija. Otro método es reducir las celdas de pista en función de algunas estrategias de resolución de problemas paso a paso. Las estrategias complejas pueden habilitarse para niveles de alta complejidad, como restar una ecuación con otra, o la mayor profundidad de los pasos de probar y verificar. Cuando aumenta el tamaño del tablero, aumenta el rango de los casos problemáticos. La relación entre el número de objetos ocultos y el número total de celdas también afecta la complejidad del rompecabezas.

las ecuaciones termodinámicas de Bridgman son un conjunto básico de ecuaciones termodinámicas, derivadas utilizando un método para generar un gran número de identidades termodinámicas que involucran un número de cantidades termodinámicas. Las ecuaciones llevan el nombre del físico estadounidense Percy Williams Bridgman . (Ver también el artículo diferencial exacto para relaciones diferenciales generales).

Las variables extensivas del sistema son fundamentales. Solo se considerarán la entropía S  , el volumen V   y los cuatro potenciales termodinámicos más comunes. Los cuatro potenciales termodinámicos más comunes son:

Energía interna	U
Entalpia	H
Helmholtz energía libre	UNA
Energía libre de Gibbs	sol

Las primeras derivadas de la energía interna con respecto a sus extensas () naturales variables de S   y V   produce los parámetros intensivo del sistema - La presión P   y la temperatura T  . Para un sistema simple en el que los números de partículas son constantes, las segundas derivadas de los potenciales termodinámicos se pueden expresar en términos de solo tres propiedades del material

capacidad calorífica (presión constante)	C P
Coeficiente de expansión termal	α
Compresibilidad isotérmica	β T

Las ecuaciones de Bridgman son una serie de relaciones entre todas las cantidades anteriores.

Introducción [ editar ]

Muchas ecuaciones termodinámicas se expresan en términos de derivadas parciales. Por ejemplo, la expresión para la capacidad de calor a presión constante es:

$${\ displaystyle C_ {P} = \ left ({\ frac {\ partial H} {\ partial T}} \ right) _ {P}}

que es la derivada parcial de la entalpía con respecto a la temperatura mientras se mantiene la presión constante. Podemos escribir esta ecuación como:

$${\ displaystyle C_ {P} = {\ frac {(\ parcial H) _ {P}} {(\ parcial T) _ {P}}}}

Este método de reescritura de la derivada parcial fue descrito por Bridgman (y también Lewis & Randall), y permite el uso de la siguiente colección de expresiones para expresar muchas ecuaciones termodinámicas. Por ejemplo de las siguientes ecuaciones tenemos:

$${\ displaystyle (\ parcial H) _ {P} = C_ {P}}

y

$${\ displaystyle (\ parcial T) _ {P} = 1}

Dividir, recuperamos la expresión adecuada para C _P .

El siguiente resumen reitera varios términos parciales en términos de los potenciales termodinámicos, los parámetros de estado S, T, P, V y las siguientes tres propiedades de los materiales que se miden fácilmente de manera experimental.

$${\ displaystyle \ left ({\ frac {\ partial V} {\ partial T}} \ right) _ {P} = \ alpha V}

$${\ displaystyle \ left ({\ frac {\ partial V} {\ partial P}} \ right) _ {T} = - \ beta _ {T} V}

$${\ displaystyle \ left ({\ frac {\ partial H} {\ partial T}} \ right) _ {P} = C_ {P} = c_ {P} N}

Ecuaciones termodinámicas de Bridgman [ editar ]

Tenga en cuenta que Lewis y Randall usan F y E para la energía de Gibbs y la energía interna, respectivamente, en lugar de G y U que se usan en este artículo.

$${\ displaystyle (\ parcial T) _ {P} = - (\ parcial P) _ {T} = 1}

$${\ displaystyle (\ parcial V) _ {P} = - (\ parcial P) _ {V} = \ izquierda ({\ frac {\ parcial V} {\ parcial T}} \ derecha) _ {P}}

$${\ displaystyle (\ parcial S) _ {P} = - (\ parcial P) _ {S} = {\ frac {C_ {p}} {T}}}

$${\ displaystyle (\ parcial U) _ {P} = - (\ parcial P) _ {U} = C_ {P} -P \ izquierda ({\ frac {\ parcial V} {\ parcial T}} \ derecha) _{PAG}}

$${\ displaystyle (\ parcial H) _ {P} = - (\ parcial P) _ {H} = C_ {P}}

$${\ displaystyle (\ parcial G) _ {P} = - (\ parcial P) _ {G} = - S}

$${\ displaystyle (\ parcial A) _ {P} = - (\ parcial P) _ {A} = - SP \ izquierda ({\ frac {\ parcial V} {\ parcial T}} \ derecha) _ {P} }

${\displaystyle (\partial V)_{T}=-(\partial T)_{V}=-\left({\frac {\partial V}{\partial P}}\right)_{T}}$

${\displaystyle (\partial S)_{T}=-(\partial T)_{S}=\left({\frac {\partial V}{\partial T}}\right)_{P}}$

${\displaystyle (\partial U)_{T}=-(\partial T)_{U}=T\left({\frac {\partial V}{\partial T}}\right)_{P}+P\left({\frac {\partial V}{\partial P}}\right)_{T}}$

${\displaystyle (\partial H)_{T}=-(\partial T)_{H}=-V+T\left({\frac {\partial V}{\partial T}}\right)_{P}}$

${\displaystyle (\partial G)_{T}=-(\partial T)_{G}=-V}$

${\displaystyle (\partial A)_{T}=-(\partial T)_{A}=P\left({\frac {\partial V}{\partial P}}\right)_{T}}$

${\displaystyle (\partial S)_{V}=-(\partial V)_{S}={\frac {C_{P}}{T}}\left({\frac {\partial V}{\partial P}}\right)_{T}+\left({\frac {\partial V}{\partial T}}\right)_{P}^{2}}$

${\displaystyle (\partial U)_{V}=-(\partial V)_{U}=C_{P}\left({\frac {\partial V}{\partial P}}\right)_{T}+T\left({\frac {\partial V}{\partial T}}\right)_{P}^{2}}$

${\displaystyle (\partial H)_{V}=-(\partial V)_{H}=C_{P}\left({\frac {\partial V}{\partial P}}\right)_{T}+T\left({\frac {\partial V}{\partial T}}\right)_{P}^{2}-V\left({\frac {\partial V}{\partial T}}\right)_{P}}$

${\displaystyle (\partial G)_{V}=-(\partial V)_{G}=-V\left({\frac {\partial V}{\partial T}}\right)_{P}-S\left({\frac {\partial V}{\partial P}}\right)_{T}}$

${\displaystyle (\partial A)_{V}=-(\partial V)_{A}=-S\left({\frac {\partial V}{\partial P}}\right)_{T}}$

${\displaystyle (\partial U)_{S}=-(\partial S)_{U}={\frac {PC_{P}}{T}}\left({\frac {\partial V}{\partial P}}\right)_{T}+P\left({\frac {\partial V}{\partial T}}\right)_{P}^{2}}$

${\displaystyle (\partial H)_{S}=-(\partial S)_{H}=-{\frac {VC_{P}}{T}}}$

${\displaystyle (\partial G)_{S}=-(\partial S)_{G}=-{\frac {VC_{P}}{T}}+S\left({\frac {\partial V}{\partial T}}\right)_{P}}$

${\displaystyle (\partial A)_{S}=-(\partial S)_{A}={\frac {PC_{P}}{T}}\left({\frac {\partial V}{\partial P}}\right)_{T}+P\left({\frac {\partial V}{\partial T}}\right)_{P}^{2}+S\left({\frac {\partial V}{\partial T}}\right)_{P}}$

${\displaystyle (\partial H)_{U}=-(\partial U)_{H}=-VC_{P}+PV\left({\frac {\partial V}{\partial T}}\right)_{P}-PC_{P}\left({\frac {\partial V}{\partial P}}\right)_{T}-PT\left({\frac {\partial V}{\partial T}}\right)_{P}^{2}}$

${\displaystyle (\partial G)_{U}=-(\partial U)_{G}=-VC_{P}+PV\left({\frac {\partial V}{\partial T}}\right)_{P}+ST\left({\frac {\partial V}{\partial T}}\right)_{P}+SP\left({\frac {\partial V}{\partial P}}\right)_{T}}$

$${\ displaystyle (\ parcial A) _ {U} = - (\ parcial U) _ {A} = P (C_ {P} + S) \ izquierda ({\ frac {\ parcial V} {\ parcial P}} \ right) _ {T} + PT \ left ({\ frac {\ partial V} {\ partial T}} \ right) _ {P} ^ {2} + ST \ left ({\ frac {\ partial V} {\ parcial T}} \ derecha) _ {P}}

$${\ displaystyle (\ parcial G) _ {H} = - (\ parcial H) _ {G} = - V (C_ {P} + S) + TS \ izquierda ({\ frac {\ parcial V} {\ parcial T}} \ derecha) _ {P}}

$${\ displaystyle (\ parcial A) _ {H} = - (\ parcial H) _ {A} = - \ izquierda [S + P \ izquierda ({\ frac {\ parcial V} {\ parcial T}} \ derecha ) _ {P} \ derecha] \ izquierda [VT \ izquierda ({\ frac {\ parcial V} {\ parcial T}} \ derecha) _ {P} \ derecha] + PC_ {P} \ izquierda ({\ frac {\ parcial V} {\ parcial P}} \ derecha) _ {T}}

$${\ displaystyle (\ parcial A) _ {G} = - (\ parcial G) _ {A} = - S \ izquierda [V + P \ izquierda ({\ frac {\ parcial V} {\ parcial P}} \ derecha) _ {T} \ derecha] -PV \ izquierda ({\ frac {\ parcial V} {\ parcial T}} \ derecha) _ {P}}