ECUACIONES

ecuación de Chapman-Kolmogorov es una identidad que relaciona las distribuciones de probabilidad conjunta de diferentes conjuntos de coordenadas en un proceso estocástico. La ecuación fue derivada de forma independiente tanto por el matemático británico Sydney Chapman como por el matemático ruso Andrey Kolmogorov .

Descripción matemática [ editar ]

Supongamos que { f _i } es una colección indexada de variables aleatorias, es decir, un proceso estocástico. Dejar

$${\ displaystyle p_ {i_ {1}, \ ldots, i_ {n}} (f_ {1}, \ ldots, f_ {n})}

ser la función de densidad de probabilidad conjunta de los valores de las variables aleatorias f ₁ a f _n . Entonces, la ecuación de Chapman – Kolmogorov es

$${\ displaystyle p_ {i_ {1}, \ ldots, i_ {n-1}} (f_ {1}, \ ldots, f_ {n-1}) = \ int _ {- \ infty} ^ {\ infty} p_ {i_ {1}, \ ldots, i_ {n}} (f_ {1}, \ ldots, f_ {n}) \, df_ {n}}

Es decir, una marginación directa sobre la variable molestia .

(Tenga en cuenta que aún no hemos asumido nada sobre el ordenamiento temporal (o cualquier otro) de las variables aleatorias, la ecuación anterior se aplica igualmente a la marginación de cualquiera de ellas).

Aplicación a las cadenas de Markov dilatadas en el tiempo [ editar ]

Cuando el proceso estocástico en consideración es markoviano , la ecuación de Chapman-Kolmogorov es equivalente a una identidad en densidades de transición. En la configuración de la cadena de Markov, se supone que i ₁  <... <  i _n . Entonces, debido a la propiedad de Markov ,

$${\ displaystyle p_ {i_ {1}, \ ldots, i_ {n}} (f_ {1}, \ ldots, f_ {n}) = p_ {i_ {1}} (f_ {1}) p_ {i_ { 2}; i_ {1}} (f_ {2} \ mid f_ {1}) \ cdots p_ {i_ {n}; i_ {n-1}} (f_ {n} \ mid f_ {n-1}) ,}

donde la probabilidad condicional $${\ displaystyle p_ {i; j} (f_ {i} \ mid f_ {j})}Es la probabilidad de transición entre los tiempos.{\ displaystyle i> j}. Así, la ecuación de Chapman-Kolmogorov toma la forma

$${\ displaystyle p_ {i_ {3}; i_ {1}} (f_ {3} \ mid f_ {1}) = \ int _ {- \ infty} ^ {\ infty} p_ {i_ {3}; i_ { 2}} (f_ {3} \ mid f_ {2}) p_ {i_ {2}; i_ {1}} (f_ {2} \ mid f_ {1}) \, df_ {2}.}

Informalmente, esto dice que la probabilidad de pasar del estado 1 al estado 3 se puede encontrar a partir de las probabilidades de pasar de 1 a un estado intermedio 2 y luego de 2 a 3, sumando todos los estados intermedios posibles 2.

Cuando la distribución de probabilidad en el espacio de estado de una cadena de Markov es discreta y la cadena de Markov es homogénea, las ecuaciones de Chapman-Kolmogorov pueden expresarse en términos de multiplicación de matriz (posiblemente infinita-dimensional) , por lo tanto:

$${\ displaystyle P (t + s) = P (t) P (s) \,}

donde P ( t ) es la matriz de transición del salto t , es decir, P ( t ) es la matriz tal que la entrada (i, j) contiene la probabilidad de que la cadena se mueva del estado i al estado j en t pasos.

Como corolario, se deduce que para calcular la matriz de transición del salto t , es suficiente elevar la matriz de transición del salto uno a la potencia de t , es decir

$${\ displaystyle P (t) = P ^ {t}. \,}

La forma diferencial de la ecuación de Chapman-Kolmogorov se conoce como ecuación maestra .

ecuación química es la representación simbólica de una reacción química en forma de símbolos y fórmulas, en donde las entidades reactantes se dan en el lado izquierdo y las entidades de producto en el lado derecho. ^[1] Los coeficientes junto a los símbolos y fórmulas de las entidades son los valores absolutos de los números estequiométricos . La primera ecuación química fue diagramada por Jean Beguin en 1615.

Formación de reacción química [ editar ]

Una ecuación química consiste en las fórmulas químicas de los reactivos (las sustancias de partida) y la fórmula química de los productos (sustancias formadas en la reacción química). Los dos están separados por un símbolo de flecha ($${\ displaystyle \ rightarrow}, generalmente se leen como "rendimientos") y la fórmula química de cada sustancia individual está separada de las demás por un signo más .

Como ejemplo, la ecuación para la reacción del ácido clorhídrico con sodio se puede denotar:

2 HCl + 2 Na → 2 NaCl + H
2

Esta ecuación se leería como "dos HCl más dos Na producen dos NaCl y H dos". Pero, para las ecuaciones que involucran productos químicos complejos, en lugar de leer la letra y su subíndice, las fórmulas químicas se leen utilizando la nomenclatura IUPAC . Usando la nomenclatura IUPAC, esta ecuación se leería como "ácido clorhídrico más sodio produce cloruro de sodio y gas hidrógeno ".

Esta ecuación indica que el sodio y HCl reaccionan para formar NaCl y H ₂ . También indica que se requieren dos moléculas de sodio por cada dos moléculas de ácido clorhídrico y la reacción formará dos moléculas de cloruro de sodio y una molécula diatómica de molécula de hidrógeno gas por cada dos moléculas de ácido clorhídrico y dos moléculas de sodio que reaccionan. Los coeficientes estequiométricos (los números frente a las fórmulas químicas) son el resultado de la ley de conservación de masa y la ley de conservación de carga (consulte la sección "Balanceo de la ecuación química" para obtener más información).

Símbolos comunes [ editar ]

Los símbolos se utilizan para diferenciar entre diferentes tipos de reacciones. Para denotar el tipo de reacción: ^[1]

• "$${\ displaystyle =}"el símbolo se utiliza para denotar una relación estequiométrica .
• "$${\ displaystyle \ rightarrow}"el símbolo se usa para denotar una reacción neta hacia adelante.
• "$${\ displaystyle \ rightleftarrows}"el símbolo se usa para denotar una reacción en ambas direcciones. ^[3]
• "{\ displaystyle {\ ce {<=>}}}"el símbolo se utiliza para denotar un equilibrio . ^[4] .

El estado físico de los productos químicos también se expresa muy comúnmente entre paréntesis después del símbolo químico, especialmente para las reacciones iónicas. Cuando se indica el estado físico, (s) denota un sólido, (l) denota un líquido, (g) denota un gas y (aq) denota una solución acuosa .

Si la reacción requiere energía, se indica sobre la flecha. Una letra griega delta delta ($${\ displaystyle \ Delta}) se coloca en la flecha de reacción para mostrar que se agrega energía en forma de calor a la reacción. $${\ displaystyle h \ nu}Se utiliza si la energía se añade en forma de luz. Otros símbolos se utilizan para otros tipos específicos de energía o radiación.

Balanceo de ecuaciones químicas [ editar ]

Visto desde la ecuación CH.
4 + 2O
2 →CO
2 + 2H
2 O, se debe colocar un coeficiente de 2 antes delgasoxígenoen el lado de los reactivos y en el lado delaguapara que, según la ley de conservación de la masa, la cantidad de cada elemento no cambie durante la reacción

P ₄ O ₁₀ + 6 H ₂ O → 4 H ₃ PO ₄
Esta ecuación química se está equilibrando multiplicando primero H ₃PO ₄ por cuatro para que coincida con el número de átomos de P, y luego multiplicando H ₂ O por seis para que coincida con los números de los átomos de H y O.

La ley de conservación de la masa dicta que la cantidad de cada elemento no cambia en una reacción química . Por lo tanto, cada lado de la ecuación química debe representar la misma cantidad de cualquier elemento en particular. Asimismo, la carga se conserva en una reacción química . Por lo tanto, la misma carga debe estar presente en ambos lados de la ecuación balanceada .

Uno equilibra una ecuación química cambiando el número escalar para cada fórmula química. Las ecuaciones químicas simples se pueden equilibrar mediante inspección, es decir, mediante prueba y error. Otra técnica consiste en resolver un sistema de ecuaciones lineales .

Las ecuaciones balanceadas se escriben con los coeficientes de números enteros más pequeños. Si no hay un coeficiente antes de una fórmula química, el coeficiente es 1.

El método de inspección se puede resumir en poner un coeficiente de 1 frente a la fórmula química más compleja y colocar los otros coeficientes antes de todo lo demás, de modo que ambos lados de las flechas tengan el mismo número de cada átomo. Si existe algún coeficiente fraccional , multiplique cada coeficiente por el número más pequeño requerido para completarlos, por lo general, el denominador del coeficiente fraccional para una reacción con un solo coeficiente fraccional.

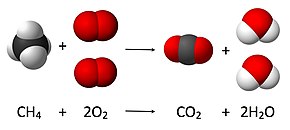
Como ejemplo, como se ve en la imagen anterior, la combustión del metano se equilibraría al poner un coeficiente de 1 antes del CH ₄ :

1 CH ₄ + O ₂ → CO ₂ + H ₂ O

Como hay un carbono en cada lado de la flecha, el primer átomo (carbono) está equilibrado.

Mirando el siguiente átomo (hidrógeno), el lado derecho tiene dos átomos, mientras que el lado izquierdo tiene cuatro. Para equilibrar los hidrógenos, 2 va delante del H ₂ O, que produce:

1 CH ₄ + O ₂ → CO ₂ + 2 H ₂ O

La inspección del último átomo a equilibrar (oxígeno) muestra que el lado derecho tiene cuatro átomos, mientras que el lado izquierdo tiene dos. Se puede equilibrar poniendo un 2 antes de O ₂ , dando la ecuación balanceada:

CH ₄ + 2 O ₂ → CO ₂ + 2 H ₂ O

Esta ecuación no tiene ningún coeficiente delante de CH ₄ y CO ₂ , ya que se cae un coeficiente de 1.

Método de matriz [ editar ]

En general, cualquier ecuación química que involucre a J diferentes moléculas puede escribirse como:

$${\ displaystyle \ sum _ {j = 1} ^ {J} \ nu _ {j} R_ {j} = 0}

donde R _j es el símbolo de la molécula j-th , y ν _j es el coeficiente estequiométrico de la molécula j-th , positivo para productos, negativo para reactivos (o viceversa). Una ecuación química adecuadamente equilibrada obedecerá:

$${\ displaystyle \ sum _ {j = 1} ^ {J} a_ {ij} \ nu _ {j} = 0}

donde la matriz de composición a _ij es el número de átomos del elemento i en la molécula j . Cualquier vector que, cuando es operado por la matriz de composición produce un vector cero, se dice que es un miembro del núcleo o espacio nulo del operador. Cualquier miembro ν _j del espacio nulo de un _ij servirá para equilibrar una ecuación química que incluya el conjunto de moléculas J que forman el sistema. Un vector estequiométrico "preferido" es uno para el cual todos sus elementos se pueden convertir en números enteros sin divisores comunes mediante la multiplicación de una constante adecuada.

En general, la matriz de la composición está degenerada: es decir, no todas sus filas serán linealmente independientes. En otras palabras, el rango ( J _R ) de la matriz de composición es generalmente menor que su número de columnas ( J ). Por el teorema de rango-nulidad , el espacio nulo de un _ij tendrá dimensiones JJ _R y este número se llama la nulidad ( J _N ) de un _ij . El problema de equilibrar una ecuación química se convierte entonces en el problema de determinar la J _N espacio nulo -dimensional de la matriz de la composición. Es importante tener en cuenta que sólo paraJ _N = 1, habrá una solución única. Para J _N > 1 habrá un número infinito de soluciones para el problema de balanceo, pero solo J _N de ellas serán independientes: si J _N puede encontrar soluciones independientes para el problema de balanceo, cualquier otra solución será una combinación lineal de estas soluciones. Si J _N = 0, no habrá solución al problema de balanceo.

Se han desarrollado técnicas ^[5] [6] para calcular rápidamente un conjunto de soluciones independientes de J _N al problema de equilibrio y son superiores a la inspección y al método algebraico en que son determinativos y proporcionan todas las soluciones al problema de equilibrio.

Ecuaciones jónicas [ editar ]

Una ecuación iónica es una ecuación química en la que los electrolitos se escriben como iones disociados . Las ecuaciones iónicas se usan para reacciones de desplazamiento simple y doble que ocurren en soluciones acuosas .

Por ejemplo, en la siguiente reacción de precipitación:

{\ displaystyle {\ ce {CaCl2 + 2AgNO3 -> Ca (NO3) 2 + 2 AgCl (v)}}}

La ecuación iónica completa es:

{\ displaystyle {\ ce {Ca ^ 2 + + 2Cl ^ - + 2Ag + + 2NO3 ^ - -> Ca ^ 2 + + 2NO3 ^ - + 2AgCl (v)}}}

En esta reacción, el Ca ²⁺ y los iones NO ₃ ^- permanecen en solución y no son parte de la reacción. Es decir, estos iones son idénticos tanto en el lado reactivo como en el lado del producto de la ecuación química. Debido a que tales iones no participan en la reacción, se les llama iones espectadores . Una ecuación iónica neta es la ecuación iónica completa de la que se han eliminado los iones espectadores. ^[7] La ecuación iónica neta de las reacciones siguientes es:

{\ displaystyle {\ ce {2Cl ^ - + 2Ag + -> 2AgCl (v)}}}

o, en forma equilibrada reducida ,

{\ displaystyle {\ ce {Ag + + Cl ^ - -> AgCl (v)}}}

En una reacción de neutralización o ácido / base , la ecuación iónica neta será generalmente:

H ⁺ (aq) + OH ^- (aq) → H ₂ O (l)

Hay algunas reacciones ácido / base que producen un precipitado además de la molécula de agua que se muestra arriba. Un ejemplo es la reacción del hidróxido de bario con ácido fosfórico , que produce no solo agua, sino también la sal insoluble fosfato de bario . En esta reacción, no hay iones espectadores, por lo que la ecuación iónica neta es la misma que la ecuación iónica completa.

{\ displaystyle {\ ce {3Ba (OH) 2 + 2H3PO4 -> 6H2O + Ba3 (PO4) 2 (v)}}}

{\ displaystyle {\ ce {3Ba2 ++ 6OH ^ {-} + 6H +}} + \ underbrace {\ ce {2PO4 ^ {3} -}} _ {\ ce {phosphate}} {\ ce {-> 6H2O + \ underbrace {Ba3 (PO4) 2 (v)} _ {bario ~ fosfato}}}}

Las reacciones de doble desplazamiento que presentan un carbonato que reacciona con un ácido tienen la ecuación iónica neta:

{\ displaystyle {\ ce {2H +}} + \ underbrace {{\ ce {CO3 ^ 2-}}} _ {{\ ce {carbonate}}} {\ ce {-> H2O + CO2 (^)}}}

Si cada ión es un "ión espectador", entonces no hubo reacción y la ecuación iónica neta es nula.

En general, si z _j es el múltiplo de la carga elemental en la molécula j-th , la neutralidad de la carga puede escribirse como:

$${\ displaystyle \ sum _ {j = 1} ^ {J} z_ {j} \ nu _ {j} = 0}

donde ν _j son los coeficientes estequiométricos descritos anteriormente. El z _j se puede incorporar ^[5] [6] como una fila adicional en el un _ij matriz descrito anteriormente, y una ecuación iónica adecuadamente equilibrado será entonces también obedecer:

$${\ displaystyle \ sum _ {j = 1} ^ {J} a_ {ij} \ nu _ {j} = 0}

teoría de campo clásica es una teoría física que predice cómo uno o más campos físicos interactúan con la materia a través de las ecuaciones de campo . El término 'teoría de campo clásica' se reserva comúnmente para describir aquellas teorías físicas que describen el electromagnetismo y la gravitación , dos de las fuerzas fundamentales de la naturaleza. Las teorías que incorporan la mecánica cuántica se denominan teorías cuánticas de campo .

Se puede pensar en un campo físico como la asignación de una cantidad física en cada punto del espacio y el tiempo . Por ejemplo, en un pronóstico del tiempo, la velocidad del viento durante un día en un país se describe asignando un vector a cada punto en el espacio. Cada vector representa la dirección del movimiento del aire en ese punto, por lo que el conjunto de todos los vectores de viento en un área en un momento dado en el tiempo constituye un campo vectorial . A medida que avanza el día, las direcciones en las que apuntan los vectores cambian a medida que cambian las direcciones del viento.

Las teorías del primer campo, la gravitación newtoniana y las ecuaciones de Maxwell de los campos electromagnéticos se desarrollaron en la física clásica antes del advenimiento de la teoría de la relatividad en 1905, y tuvieron que ser revisadas para que fueran compatibles con esa teoría. En consecuencia, las teorías de campo clásicas se clasifican generalmente como no relativistas y relativistas . Las teorías de campo modernas generalmente se expresan usando las matemáticas del cálculo tensorial . Un formalismo matemático alternativo más reciente describe los campos clásicos como secciones de objetos matemáticos llamados paquetes de fibra .

En 1839, James MacCullagh presentó ecuaciones de campo para describir la reflexión y la refracción en "Un ensayo hacia una teoría dinámica de la reflexión y refracción cristalina". 

Teorías de campo no relativista [ editar ]

Algunos de los campos físicos más simples son los campos de fuerza vectorial. Históricamente, la primera vez que se tomaron en serio los campos fue con las líneas de fuerza de Faraday al describir el campo eléctrico . El campo gravitatorio fue entonces descrito de manera similar.

La gravitación newtoniana [ editar ]

La primera teoría de campo de la gravedad fue la teoría de Newton de la gravitación, en la que la interacción mutua entre dos masas obedece a una ley del cuadrado inverso . Esto fue muy útil para predecir el movimiento de los planetas alrededor del Sol.

Cualquier cuerpo masivo M tiene un campo gravitatorio g que describe su influencia en otros cuerpos masivos. El campo gravitatorio de M en un punto r en el espacio se encuentra determinando la fuerza F que M ejerce sobre una pequeña masa de prueba m ubicada en r , y luego dividiendo por m : ^[2]

$${\ displaystyle \ mathbf {g} (\ mathbf {r}) = {\ frac {\ mathbf {F} (\ mathbf {r})} {m}}.}

Estipulando que m es mucho menor que M asegura que la presencia de m tiene una influencia insignificante sobre el comportamiento de M .

De acuerdo con la ley de gravitación universal de Newton , F ( r ) viene dada por ^[2]

$${\ displaystyle \ mathbf {F} (\ mathbf {r}) = - {\ frac {GMm} {r ^ {2}}} {\ hat {\ mathbf {r}}},}

dónde $${\ displaystyle {\ hat {\ mathbf {r}}}}es un vector unitario que apunta a lo largo de la línea de M a m , y G es la constante gravitacional de Newton . Por lo tanto, el campo gravitacional de M es ^[2]

$${\ displaystyle \ mathbf {g} (\ mathbf {r}) = {\ frac {\ mathbf {F} (\ mathbf {r})} {m}} = - {\ frac {GM} {r ^ {2 }}} {\ hat {\ mathbf {r}}}.}

La observación experimental de que la masa inercial y la masa gravitatoria son iguales a niveles de precisión sin precedentes conduce a la identificación de la intensidad del campo gravitatorio como idéntica a la aceleración experimentada por una partícula. Este es el punto de partida del principio de equivalencia , que conduce a la relatividad general .

Para una colección discreta de masas, M _i , ubicada en puntos, r _i , el campo gravitacional en un punto r debido a las masas es

$${\ displaystyle \ mathbf {g} (\ mathbf {r}) = - G \ sum _ {i} {\ frac {M_ {i} (\ mathbf {r} - \ mathbf {r_ {i}})} { | \ mathbf {r} - \ mathbf {r} _ {i} | ^ {3}}} \ ,,}

Si tenemos una distribución de masa continua ρ en cambio, la suma se reemplaza por una integral,

$${\ displaystyle \ mathbf {g} (\ mathbf {r}) = - G \ iiint _ {V} {\ frac {\ rho (\ mathbf {x}) d ^ {3} \ mathbf {x} (\ mathbf {r} - \ mathbf {x})} {| \ mathbf {r} - \ mathbf {x} | ^ {3}}} \ ,,}

Tenga en cuenta que la dirección del campo apunta desde la posición r a la posición de las masas r _i ; Esto está asegurado por el signo menos. En pocas palabras, esto significa que todas las masas se atraen.

En la forma integral la ley de Gauss para la gravedad es

$${\ displaystyle \ iint \ mathbf {g} \ cdot d \ mathbf {S} = -4 \ pi GM}

mientras que en forma diferencial es

$${\ displaystyle \ nabla \ cdot \ mathbf {g} = -4 \ pi G \ rho _ {m}}

Por lo tanto, el campo gravitacional g se puede escribir en términos del gradiente de un potencial gravitacional φ ( r ):

$${\ displaystyle \ mathbf {g} (\ mathbf {r}) = - \ nabla \ phi (\ mathbf {r}).}

Esto es una consecuencia de que la fuerza gravitacional F es conservadora .

Electromagnetismo [ editar ]

Electrostática [ editar ]

Artículo principal: Electrostática

Una partícula de prueba cargada con carga q experimenta una fuerza F basada únicamente en su carga. Podemos describir de manera similar el campo eléctrico E de manera que F = q E . Usando esto y la ley de Coulomb, el campo eléctrico debido a una sola partícula cargada es

$${\ displaystyle \ mathbf {E} = {\ frac {1} {4 \ pi \ epsilon _ {0}}} {\ frac {q} {r ^ {2}}} {\ hat {\ mathbf {r} }} \ ,.}

El campo eléctrico es conservador , y por lo tanto está dado por el gradiente de un potencial escalar, V ( r )

$${\ displaystyle \ mathbf {E} (\ mathbf {r}) = - \ nabla V (\ mathbf {r}) \ ,.}

La ley de Gauss para la electricidad está en forma integral.

$${\ displaystyle \ iint \ mathbf {E} \ cdot d \ mathbf {S} = {\ frac {q_ {e}} {\ epsilon _ {0}}}}

mientras que en forma diferencial

$${\ displaystyle \ nabla \ cdot \ mathbf {E} = {\ frac {\ rho _ {e}} {\ epsilon _ {0}}} \ ,.}

Magnetostática [ editar ]

Artículo principal: Magnetostática

Una corriente constante I que fluye a lo largo de un camino ℓ ejercerá una fuerza sobre las partículas cargadas cercanas que es cuantitativamente diferente de la fuerza del campo eléctrico descrito anteriormente. La fuerza ejercida por I en una carga cercana q con velocidad v es

$${\ displaystyle \ mathbf {F} (\ mathbf {r}) = q \ mathbf {v} \ times \ mathbf {B} (\ mathbf {r}),}

donde B ( r ) es el campo magnético , que se determina a partir de I por la ley Biot-Savart :

$${\ displaystyle \ mathbf {B} (\ mathbf {r}) = {\ frac {\ mu _ {0} I} {4 \ pi}} \ int {\ frac {d {\ boldsymbol {\ ell}} \ veces d {\ hat {\ mathbf {r}}}} {r ^ {2}}}.}

El campo magnético no es conservador en general, y por lo tanto, generalmente no puede escribirse en términos de un potencial escalar. Sin embargo, se puede escribir en términos de un potencial vectorial , A ( r ):

$${\ displaystyle \ mathbf {B} (\ mathbf {r}) = \ nabla \ times \ mathbf {A} (\ mathbf {r})}

La ley de Gauss para el magnetismo en forma integral es

$${\ displaystyle \ iint \ mathbf {B} \ cdot d \ mathbf {S} = 0,}

mientras que en forma diferencial es

$${\ displaystyle \ nabla \ cdot \ mathbf {B} = 0.}

La interpretación física es que no hay monopolos magnéticos .

Electrodinámica [ editar ]

Artículo principal: Electrodinámica.

En general, en presencia de una densidad de carga ρ ( r , t ) y una densidad de corriente J ( r , t ), habrá un campo eléctrico y un campo magnético, y ambos variarán en el tiempo. Están determinados por las ecuaciones de Maxwell , un conjunto de ecuaciones diferenciales que se relacionan directamente E y B a la densidad de carga eléctrica (carga por unidad de volumen) ρ y densidad de corriente (corriente eléctrica por unidad de área) J. ^[3]

Alternativamente, se puede describir el sistema en términos de su escalares y vectoriales potenciales V y A . Un conjunto de ecuaciones integrales conocidas como potenciales retardados permiten calcular V y A a partir de ρ y J , ^{[nota 1]} y desde allí los campos eléctrico y magnético se determinan a través de las relaciones ^[4]

$${\ displaystyle \ mathbf {E} = - \ nabla V - {\ frac {\ partial \ mathbf {A}} {\ partial t}}}

$${\ displaystyle \ mathbf {B} = \ nabla \ times \ mathbf {A}.}

Hidrodinámica [ editar ]

Artículo principal: Hidrodinámica.

La dinámica de fluidos tiene campos de presión, densidad y caudal que están conectados por las leyes de conservación para la energía y el impulso. La ecuación de continuidad de masa es una ecuación de continuidad, que representa la conservación de la masa.

$${\ displaystyle {\ frac {\ partial \ rho} {\ partial t}} + \ nabla \ cdot (\ rho \ mathbf {u}) = 0}

y las ecuaciones de Navier-Stokes representan la conservación del momento en el fluido, que se encuentra en las leyes de Newton aplicadas al fluido,

$${\ displaystyle {\ frac {\ partial} {\ partial t}} (\ rho \ mathbf {u}) + \ nabla \ cdot (\ rho \ mathbf {u} \ otimes \ mathbf {u} + p \ mathbf { I}) = \ nabla \ cdot {\ boldsymbol {\ tau}} + \ rho \ mathbf {b}}

si se dan la densidad ρ , la presión p , el tensor de tensión desviadora τ del fluido, así como las fuerzas externas del cuerpo b . El campo de velocidad u es el campo vectorial para resolver.

La teoría del potencial [ editar ]

El término " teoría del potencial " surge del hecho de que, en la física del siglo XIX, se creía que las fuerzas fundamentales de la naturaleza derivaban de potenciales escalares que satisfacían la ecuación de Laplace . Poisson abordó la cuestión de la estabilidad de las órbitas planetarias , que ya había sido resuelta por Lagrange al primer grado de aproximación de las fuerzas de perturbación, y derivó la ecuación de Poisson , que lleva su nombre. La forma general de esta ecuación es

$${\ displaystyle \ nabla ^ {2} \ phi = \ sigma}

donde σ es una función de fuente (como densidad, una cantidad por unidad de volumen) y potential el potencial escalar para resolver.

En la gravitación newtoniana; las masas son las fuentes del campo, de modo que las líneas de campo terminan en los objetos que tienen masa. De manera similar, las cargas son las fuentes y los sumideros de los campos electrostáticos: las cargas positivas emanan de las líneas de campo eléctrico, y las líneas de campo terminan en cargas negativas. Estos conceptos de campo también se ilustran en el teorema general de la divergencia , específicamente la ley de Gauss para la gravedad y la electricidad. Para los casos de gravedad independiente y electromagnetismo, los campos son gradientes de potenciales correspondientes.

$${\ displaystyle \ mathbf {g} = - \ nabla \ phi _ {g} \ ,, \ quad \ mathbf {E} = - \ nabla \ phi _ {e}}

por lo que sustituyendo estos en la ley de Gauss para cada caso obtiene

$${\ displaystyle \ nabla ^ {2} \ phi = 4 \ pi G \ rho _ {g} \ ,, \ quad \ nabla ^ {2} \ phi = - {\ rho _ {e} \ over \ epsilon _ { 0}}}

donde ρ _g es la densidad de masa y ρ _e la densidad de carga .

Por cierto, esta similitud surge de la similitud entre la ley de gravitación de Newton y la ley de Coulomb .

En el caso de que no haya un término fuente (por ejemplo, vacío, o cargas pareadas), estos potenciales obedecen a la ecuación de Laplace :

$${\ displaystyle \ nabla ^ {2} \ phi = 0}

Para una distribución de masa (o carga), el potencial se puede desarrollar en una serie de armónicos esféricos , y el n º término en la serie puede ser visto como un potencial que surge de los 2 ⁿ -moments (ver desarrollo multipolar ). Para muchos propósitos, solo se necesitan los términos monopolo, dipolo y cuadrupolo en los cálculos.

La teoría de campos relativista [ editar ]

Artículo principal: Teoría del campo clásica covariante.

Las formulaciones modernas de las teorías de campo clásicas generalmente requieren la covarianza de Lorentz,ya que ahora se reconoce como un aspecto fundamental de la naturaleza. Una teoría de campo tiende a expresarse matemáticamente mediante el uso de lagrangianos . Esta es una función que, cuando está sujeta a un principio de acción , da lugar a las ecuaciones de campo y una ley de conservación para la teoría. La acciónes un escalar de Lorentz, del cual se pueden derivar fácilmente las ecuaciones de campo y las simetrías.

En todas partes utilizamos unidades de modo que la velocidad de la luz en el vacío es 1, es decir, c = 1. ^{[nota 2]}

Dinámica Lagrangiana [ editar ]

Artículo principal: lagrangiano (teoría de campo)

Dado un tensor de campo φ , un escalar llamado densidad lagrangiana

$${\ displaystyle {\ mathcal {L}} (\ phi, \ partial \ phi, \ partial \ partial \ phi, \ ldots, x)}

Se puede construir a partir de φ y sus derivados.

A partir de esta densidad, la acción funcional se puede construir mediante la integración en el espacio-tiempo,

$${\ displaystyle {\ mathcal {S}} = \ int {{\ mathcal {L}} {\ sqrt {-g}} \, \ mathrm {d} ^ {4} x}.}

Dónde $${\ displaystyle {\ sqrt {-g}}} se ve como el 'jacobiano' en el espacio-tiempo curvo. $${\ displaystyle (g \ equiv {\ text {det}} (g _ {\ mu \ nu}))}

Por lo tanto, el Lagrangiano en sí mismo es igual a la integral de la densidad Lagrangiana en todo el espacio.

Luego, al aplicar el principio de acción , se obtienen las ecuaciones de Euler-Lagrange.

$${\ displaystyle {\ frac {\ delta {\ mathcal {S}}} {\ delta \ phi}} = {\ frac {\ partial {\ partial {\ mathcal {L}}} {\ partial \ phi}} - \ partial _ {\ mu} \ left ({\ frac {\ partial {\ mathcal {L}}} {\ partial (\ partial _ {\ mu} \ phi)}} \ right) + \ cdots + (- 1) ^ { m} \ parcial _ {\ mu _ {1}} \ parcial _ {\ mu _ {2}} \ cdots \ parcial _ {\ mu _ {m-1}} \ parcial _ {\ mu _ {m}} \ left ({\ frac {\ partial {\ mathcal {L}}} {\ partial (\ partial _ {\ mu _ {1}} \ partial _ {\ mu _ {2}} \ cdots \ partial _ {\ mu _ {m-1}} \ parcial _ {\ mu _ {m}} \ phi)}} \ derecha) = 0.}

Campos relativistas [ editar ]

Ahora se describen dos de las teorías de campo clásicas de Lorentz covariante más conocidas.

Electromagnetismo [ editar ]

Artículos principales: Campo electromagnético y electromagnetismo.

Históricamente, las primeras teorías de campo (clásicas) fueron las que describían los campos eléctrico y magnético (por separado). Después de numerosos experimentos, se encontró que estos dos campos estaban relacionados, o, de hecho, dos aspectos del mismo campo: el campo electromagnético . Maxwell teoría de la 's electromagnetismo describe la interacción de materia cargada con el campo electromagnético. La primera formulación de esta teoría de campo utilizó campos vectoriales para describir los campos eléctrico y magnético . Con la llegada de la relatividad especial, una formulación más completa con tensor.Se encontraron campos. En lugar de usar dos campos vectoriales que describen los campos eléctrico y magnético, se usa un campo tensor que representa estos dos campos juntos.

El cuatro potencial electromagnético se define como A _a = (- φ , A ), y el cuatro corriente electromagnética j _a = (- ρ , j ). El campo electromagnético en cualquier punto del espacio-tiempo se describe mediante el tensor de campo electromagnético antisimétrico (0,2)

$${\ displaystyle F_ {ab} = \ parcial _ {a} A_ {b} - \ parcial _ {b} A_ {a}.}

El lagrangiano [ editar ]

Para obtener la dinámica para este campo, intentamos construir un escalar desde el campo. En el vacío, tenemos

$${\ displaystyle {\ mathcal {L}} = - {\ frac {1} {4 \ mu _ {0}}} F ^ {ab} F_ {ab} \ ,.}

Podemos usar la teoría del campo de medición para obtener el término de interacción, y esto nos da

$${\ displaystyle {\ mathcal {L}} = - {\ frac {1} {4 \ mu _ {0}}} F ^ {ab} F_ {ab} + j ^ {a} A_ {a} \ ,. }

Las ecuaciones [ editar ]

Para obtener las ecuaciones de campo, el tensor electromagnético en la densidad de Lagrangian debe ser reemplazado por su definición en términos del potencial A de 4 , y es este potencial el que ingresa en las ecuaciones de Euler-Lagrange. El campo F de EM no se varía en las ecuaciones de EL. Por lo tanto,

$${\ displaystyle \ partial _ {b} \ left ({\ frac {\ partial {\ mathcal {L}}} {\ partial \ left (\ partial _ {b} A_ {a} \ right)}} \ right) = {\ frac {\ partial {\ mathcal {L}}} {\ partial A_ {a}}} \ ,.}

Evaluar la derivada de la densidad lagrangiana con respecto a los componentes del campo.

$${\ displaystyle \ partial {\ mathcal {L}} / \ partial A_ {a} = \ mu _ {0} j ^ {a} \ ,,}

y los derivados de los componentes de campo.

$${\ displaystyle \ partial {\ mathcal {L}} / \ partial (\ partial _ {b} A_ {a}) = F ^ {ab} \ ,,}

Obtiene las ecuaciones de Maxwell en vacío. Las ecuaciones de origen (ley de Gauss para la electricidad y ley de Maxwell-Ampère) son

$${\ displaystyle \ parcial _ {b} F ^ {ab} = \ mu _ {0} j ^ {a} \ ,.}

mientras que los otros dos (la ley de Gauss para el magnetismo y la ley de Faraday) se obtienen del hecho de que F es el rizo 4 de A , o, en otras palabras, del hecho de que la identidad del bianchi es válida para el tensor del campo electromagnético. ^[5]

$${\ displaystyle 6F _ {[ab, c]} \, = F_ {ab, c} + F_ {ca, b} + F_ {bc, a} = 0.}

donde la coma indica una derivada parcial .

Gravitación [ editar ]

Artículos principales: Gravitación , relatividad general y ecuación de campo de Einstein

Después de que se descubrió que la gravitación newtoniana era incompatible con la relatividad especial , Albert Einstein formuló una nueva teoría de la gravitación llamada relatividad general . Esto trata a la gravitación como un fenómeno geométrico (' espacio-tiempo curvo ') causado por masas y representa matemáticamente el campo gravitacional por un campo tensor llamado tensor métrico . Las ecuaciones de campo de Einstein describen cómo se produce esta curvatura. La gravitación newtoniana es ahora reemplazado por Einstein teoría de la 's relatividad general , en la queSe piensa que la gravitación se debe a un espacio-tiempo curvo , causado por masas. La ecuación de campo de Einstein describe cómo esta curvatura es producida por masas,

$${\ displaystyle G_ {ab} = \ kappa T_ {ab}}

donde κ = 8πG / c ⁴ es una constante que aparece en las ecuaciones de campo de Einstein (y no en la acción), y

$${\ displaystyle G_ {ab} \, = R_ {ab} - {\ frac {R} {2}} g_ {ab}}

Es el tensor de Einstein . Una interpretación alternativa, debida a Arthur Eddington , es que$${\ displaystyle R} es fundamental, $${\ displaystyle T}es meramente un aspecto de $${\ displaystyle R}y $${\ displaystyle \ kappa} Está obligado por la elección de las unidades.

La solución de vacío se puede obtener variando la siguiente acción de Einstein-Hilbert con respecto a la métrica

$${\ displaystyle S [g] = k \ int R {\ sqrt {-g}} \, d ^ {4} x}

Las ecuaciones de campo de vacío son las ecuaciones de campo escritas sin materia (incluidas las fuentes). Las soluciones de las ecuaciones de campo de vacío se llaman soluciones de vacío . Las ecuaciones de campo pueden derivarse utilizando la acción de Einstein-Hilbert . Variando el lagrangiano

$${\ displaystyle {\ mathcal {L}} = R {\ sqrt {-g}} \ ,,}

donde R = R _ab g ^ab es el escalar de Ricci escrito en términos del tensor de Ricci R _ab y g el determinante del tensor métrico g ^ab producirá las ecuaciones del campo de vacío

$${\ displaystyle G_ {ab} = 0 \ ,.}

Intentos de unificación [ editar ]

Artículo principal: Teorías de campo unificadas clásicas.

Los intentos de crear una teoría de campo unificada basada en la física clásica son teorías de campo unificadas clásicas. Durante los años entre las dos guerras mundiales, la idea de la unificación de la gravedad con el electromagnetismo fue perseguida activamente por varios matemáticos y físicos como Albert Einstein , Theodor Kaluza ^[6] , Hermann Weyl ^[7] , Arthur Eddington ^[8] , Gustav Mie ^{[ 9]} y Ernst Reichenbacher. ^[10]

Los primeros intentos para crear dicha teoría se basaron en la incorporación de campos electromagnéticos en la geometría de la relatividad general . En 1918, el caso de la primera geometrización del campo electromagnético fue propuesto en 1918 por Hermann Weyl. ^[11] En 1919, una idea de enfoque en cinco dimensiones sugerida por Theodor Kaluza . ^[11] A partir de eso, se desarrolló una teoría llamada Teoría de Kaluza-Klein . Intenta unificar la gravitación y el electromagnetismo , en un espacio-tiempo de cinco dimensiones.. Hay varias formas de ampliar el marco representativo para una teoría de campo unificada que han sido consideradas por Einstein y otros investigadores. Estas extensiones en general se basan en dos opciones. ^[11] La primera opción se basa en relajar las condiciones impuestas en la formulación original, y la segunda se basa en la introducción de otros objetos matemáticos en la teoría. ^[11] Un ejemplo de la primera opción es relajar las restricciones al espacio-tiempo de cuatro dimensiones al considerar representaciones de dimensiones superiores. ^[11] Eso se usa en la teoría de Kaluza-Klein . Para el segundo, el ejemplo más prominente surge del concepto de la conexión afín que se introdujo enLa teoría de la relatividad general, principalmente a través del trabajo de Tullio Levi-Civita y Hermann Weyl . ^[11]

El desarrollo posterior de la teoría de campos cuánticos cambió el enfoque de la búsqueda de la teoría de campos unificados de la descripción clásica a la cuántica. Debido a eso, muchos físicos teóricos abandonaron la búsqueda de una teoría clásica de campos unificados. ^[11] La teoría cuántica de campos incluiría la unificación de otras dos fuerzas fundamentales de la naturaleza , una fuerza nuclear fuerte y débil que actúa a nivel subatómico.