GEOMETRÍA CLÁSICA

GEOMETRÍA PROYECTIVA

secuencia de Euler es una secuencia exacta particular de gavillas en el espacio proyectivo n- dimensional sobre un anillo . Muestra que la gavilla de diferenciales relativos es establemente isomorfa a una  suma ( n + 1) de la doble de la gavilla en espiral Serre .

La secuencia de Euler se generaliza a la de un paquete proyectivo , así como a un paquete de Grassmann(consulte el último artículo para esta generalización).

Declaración [ editar ]

Para A a ring, hay una secuencia exacta de gavillas

$${\ displaystyle 0 \ to \ Omega _ {\ mathbb {P} _ {A} ^ {n} / A} ^ {1} \ to {\ mathcal {O}} _ {\ mathbb {P} _ {A} ^ {n}} (- 1) ^ {\ oplus n + 1} \ to {\ mathcal {O}} _ {\ mathbb {P} _ {A} ^ {n}} \ a 0.}

Se puede probar definiendo un homomorfismo. $${\ displaystyle S (-1) ^ {\ oplus n + 1} \ a S, e_ {i} \ mapsto x_ {i}} con $${\ displaystyle S = A [x_ {0}, \ ldots, x_ {n}]} y $${\ displaystyle e_ {i} = 1}en grado 1, suryectivo en grados $${\ displaystyle \ geq 1}y verificando que localmente en los  gráficos estándar n + 1, el núcleo es isomorfo al módulo diferencial relativo. ^[1]

Interpretación geométrica [ editar ]

Suponemos que A es un campo k .

La secuencia exacta anterior es equivalente a la secuencia

$${\ displaystyle 0 \ to {\ mathcal {O}} _ {\ mathbb {P} ^ {n}} \ to {\ mathcal {O}} (1) ^ {\ oplus (n + 1)} \ to { \ mathcal {T}} _ {\ mathbb {P} ^ {n}} \ a 0},

donde el último término distinto de cero es la gavilla tangente .

Consideramos V a n + 1 espacio vectorial dimensional sobre k , y explicamos la secuencia exacta

$${\ displaystyle 0 \ to {\ mathcal {O}} _ {\ mathbb {P} (V)} \ to {\ mathcal {O}} _ {\ mathbb {P} (V)} (1) \ otimes V \ a {\ mathcal {T}} _ {\ mathbb {P} (V)} \ a 0}

Esta secuencia se entiende más fácilmente mediante la interpretación del término central como la gavilla de 1-homogéneos campos de vectores en el espacio vectorial V . Existe una sección notable de esta gavilla, el campo vectorial de Euler , tautológicamente definido al asociar a un punto del espacio vectorial el vector tangente asociado de manera idéntica ( es decir, a sí mismo: es el mapa de identidad visto como un campo vectorial).

Este campo vectorial es radial en el sentido de que se desvanece uniformemente en las funciones 0-homogéneas, es decir, las funciones que son invariantes por reescalado homotético, o " independiente de la coordenada radial ".

Una función (definida en algún conjunto abierto) en $${\ displaystyle \ mathbb {P} (V)}da lugar al retroceso a una función 0-homogénea en V(de nuevo parcialmente definida). Obtenemos campos vectoriales 1-homogéneos multiplicando el campo vectorial de Euler por tales funciones. Esta es la definición del primer mapa, y su inyectividad es inmediata.

El segundo mapa está relacionado con la noción de derivación, equivalente a la del campo vectorial. Recuerde que un campo vectorial en un conjunto abierto U del espacio proyectivo$${\ displaystyle \ mathbb {P} (V)}se puede definir como una derivación de las funciones definidas en este conjunto abierto. Al retroceder en V , esto es equivalente a una derivación en la preimagen de U que conserva las funciones 0-homogéneas. Cualquier campo vectorial en$${\ displaystyle \ mathbb {P} (V)}se puede obtener de este modo, y el defecto de inyectividad de este mapeo consiste precisamente en los campos vectoriales radiales.

Vemos, por lo tanto, que el núcleo del segundo morfismo se identifica con el rango del primero.

El paquete de líneas canónicas de espacios proyectivos [ editar ]

Al tomar el poder exterior más alto , uno ve que la gavilla canónica de un espacio proyectivo está dada por

$${\ displaystyle \ omega _ {\ mathbb {P} _ {A} ^ {n} / A} = {\ mathcal {O}} _ {\ mathbb {P} _ {A} ^ {n}} (- ( n + 1))}.

En particular, los espacios proyectivas son variedades de Fano , porque el haz canónica es anti- amplio y esta línea paquete no tiene distintas de cero secciones globales, por lo que el género geométrica es 0.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

El avion fano

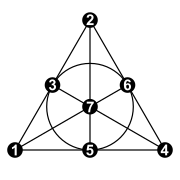
En geometría finita , el plano Fano (después de Gino Fano ) es el plano proyectivo finito de orden 2. Es el plano proyectivo finito con el menor número posible de puntos y líneas: 7 puntos y 7 líneas, con 3 puntos en cada línea y 3 líneas a través de cada punto. La notación estándar para este plano, como miembro de una familia de espacios proyectivos , es PG (2, 2), donde PG significa " Geometría proyectiva ", el primer parámetro es la dimensión geométrica y el segundo parámetro es el orden.

El plano Fano es un ejemplo de una estructura de incidencia finita , por lo que muchas de sus propiedades pueden establecerse utilizando técnicas combinatorias y otras herramientas utilizadas en el estudio de las geometrías de incidencia . Dado que es un espacio proyectivo, las técnicas algebraicas también pueden ser herramientas efectivas en su estudio.

Coordenadas homogéneas [ editar ]

El plano de Fano se puede construir a través del álgebra lineal como el plano proyectivo sobre el campo finitocon dos elementos. De manera similar, se pueden construir planos proyectivos sobre cualquier otro campo finito, siendo el plano Fano el más pequeño.

Usando la construcción estándar de espacios proyectivos a través de coordenadas homogéneas , los siete puntos del plano de Fano se pueden etiquetar con los siete triples ordenados no cero de los dígitos binarios 001, 010, 011, 100, 101, 110 y 111. Esto puede ser hecho de tal manera que por cada dos puntos p y q , el tercer punto en la línea pq tiene la etiqueta formada al agregar las etiquetas de p y q módulo 2. En otras palabras, los puntos del plano de Fano se corresponden con los no - Puntos cero del espacio vectorial finito de dimensión 3 sobre el campo finito de orden 2.

Debido a esta construcción, el plano Fano se considera un plano desarguesiano , aunque el plano es demasiado pequeño para contener una configuración Desargues no degenerada (que requiere 10 puntos y 10 líneas).

A las líneas del plano de Fano también se les pueden dar coordenadas homogéneas, nuevamente utilizando triples no cero de dígitos binarios. Con este sistema de coordenadas, un punto incide en una línea si la coordenada para el punto y la coordenada para la línea tienen un número par de posiciones en las que ambos tienen bits distintos de cero: por ejemplo, el punto 101 pertenece a la línea 111 , porque tienen bits distintos de cero en dos posiciones comunes. En términos del álgebra lineal subyacente, un punto pertenece a una línea si el producto interno de los vectores que representan el punto y la línea es cero.

Las líneas se pueden clasificar en tres tipos.

• En tres de las líneas, los triples binarios para los puntos tienen el 0 en una posición constante: la línea 100 (que contiene los puntos 001, 010 y 011) tiene 0 en la primera posición, y las líneas 010 y 001 se forman en la primera posición. mismo camino.
• En tres de las líneas, dos de las posiciones en los triples binarios de cada punto tienen el mismo valor: en la línea 110 (que contiene los puntos 001, 110 y 111) la primera y la segunda posición son siempre iguales, y las líneas 101 y 011 se forman de la misma manera.
• En la línea restante 111 (que contiene los puntos 011, 101 y 110), cada triple binario tiene exactamente dos bits distintos de cero.

Grupo de la teoría de la construcción [ editar ]

Alternativamente, los 7 puntos del plano corresponden a los 7 elementos de no identidad del grupo ( Z ₂ ) ³ = Z ₂× Z ₂ × Z ₂ . Las líneas del plano corresponden a los subgrupos de orden 4, isomorfos a Z ₂ × Z ₂ . El grupo de automorfismo GL (3,2) del grupo ( Z ₂ ) ³ es el del plano Fano, y tiene un orden 168.

Gráfico de Levi [ editar ]

Gráfico bipartito de Heawood. Los puntos están representados por vértices de un color y líneas por vértices del otro color.

Al igual que con cualquier estructura de incidencia, el gráfico Levi del plano Fano es un gráfico bipartito , los vértices de una parte representan los puntos y el otro representa las líneas, con dos vértices unidos si el punto y la línea correspondientes son incidentes . Este gráfico en particular es un gráfico cúbico conectado (regular de grado 3), tiene una circunferencia 6 y cada parte contiene 7 vértices. Es el gráfico de Heawood , el único 6-jaula . ^[1]

Collineations [ editar ]

Colineación del plano de Fano correspondiente a la permutación del código Gray de3 bits.

Una permutación de los siete puntos del plano Fano que transporta puntos colineales (puntos en la misma línea) a puntos colineales (en otras palabras, "preserva la colinealidad") se denomina " colinción ", " automorfismo " o " simetría " del avion El grupo de colineación completa (o grupo de automorfismo, o grupo de simetría ) es el grupo lineal proyectivo PGL (3,2) ^[2] que en este caso es isomorfo al grupo lineal especial proyectivo PSL (3,2) , y el general lineal grupoGL (3,2) (que es igual a PGL (3,2), porque el campo tiene solo un elemento distinto de cero) y también es isomorfo a PSL (2,7). ^[3] Consta de 168 permutaciones diferentes.

Como un grupo de permutación que actúa sobre los puntos del plano, el grupo de colineación es doblemente transitivo, lo que significa que cualquier par de puntos ordenados puede ser mapeado por al menos una colinción a cualquier otro par de puntos ordenados. ^[4]

Las colinciones también pueden verse como los automorfismos que preservan el color del gráfico de Heawood.

Dualidad en el plano de Fano: cada punto corresponde a una línea y viceversa.

Dualidades [ editar ]

Artículo principal: Dualidad (geometría proyectiva).

Una bijección entre el conjunto de puntos y el conjunto de líneas que preserva la incidencia se denomina dualidad y la dualidad de orden dos se denomina polaridad . ^[5]

Las dualidades se pueden ver en el contexto del gráfico de Heawood como automorfismos de inversión de color. Un ejemplo de una polaridad se da por reflexión a través de una línea vertical que biseca la representación del gráfico de Heawood que se muestra a la derecha. ^[6]La existencia de esta polaridad muestra que el plano Fano es auto-dual . Esto también es una consecuencia inmediata de la simetría entre puntos y líneas en la definición de la relación de incidencia en términos de coordenadas homogéneas, como se detalla en una sección anterior.

Estructura del grupo de automorfismo [ editar ]

Un etiquetado nimber del plano fano.

Con las etiquetas nimber de la figura adjunta, el grupo de colineación del plano Fano, presentado como un grupo de permutación, puede generarse mediante las permutaciones dadas en notación cíclica por: ^[7]

⟨(1432657), (162) (374), (14) (27), (17) (24), (17) (24) (36).

El grupo de colineación se compone de 6 clases de conjugación . 
Todas las estructuras de ciclo, excepto el de 7 ciclos, definen de manera única una clase de conjugación:

•  La permutación de la identidad.
• 21 permutaciones con dos 2 ciclos.
•  42 permutaciones con 4 ciclos y 2 ciclos.
•  56 permutaciones con dos 3 ciclos.

Las 48 permutaciones con un ciclo completo de 7 forman dos clases de conjugación distintas con 24 elementos:

•  Una mapas a la B , B a C , C a D . Entonces D está en la misma línea que A y B .
•  Una mapas a la B , B a C , C a D . Entonces D está en la misma línea que A y C .

Vea las colinciones del avión de Fano para una lista completa.

Por lo tanto, según el teorema de enumeración de Pólya , el número de colorantes desiguales del plano de Fano con n colores es:

$${\ displaystyle {1 \ sobre 168} \ izquierda (n ^ {7} + 21n ^ {5} + 98n ^ {3} + 48n \ derecha).}

Cuadrados completos y subplanos de Fano [ editar ]

Artículo principal: Cuadrángulo completo

En cualquier plano proyectivo, un conjunto de cuatro puntos, no tres de los cuales son colineales, y las seis líneas que unen pares de estos puntos son una configuración conocida como un cuadrángulo completo . Las líneas se llaman lados y los pares de lados que no se encuentran en uno de los cuatro puntos se llaman lados opuestos . Los puntos en los que se encuentran los lados opuestos se llaman puntos diagonales y hay tres de ellos. ^[8]

Si esta configuración se encuentra en un plano proyectivo y los tres puntos diagonales son colineales, los siete puntos y las siete líneas de la configuración expandida forman un subplano del plano proyectivo que es isomorfo al plano de Fano y se llama un subplano de Fano .

Un resultado famoso, debido a Andrew M. Gleason, establece que si cada cuadrángulo completo en un plano proyectivo finito se extiende a un subplano Fano (es decir, tiene puntos diagonales colineales), entonces el plano es Desarguesiano. ^[9] Gleason llamó a cualquier plano proyectivo que satisface esta condición un plano de Fano , creando así cierta confusión con la terminología moderna. Para agravar la confusión, el axioma de Fanoestablece que los puntos diagonales de un cuadrángulo completo nunca son colineales, una condición que se mantiene en los planos euclidianos y proyectivos reales. Por lo tanto, lo que Gleason llama aviones de Fano no satisface el axioma de Fano. ^[10]

Configuraciones [ editar ]

El plano de Fano contiene los siguientes números de configuraciones de puntos y líneas de diferentes tipos. Para cada tipo de configuración, el número de copias de configuración multiplicado por el número de simetrías del plano que mantiene la configuración sin cambios es igual a 168, el tamaño de todo el grupo de colineación, siempre que cada copia se pueda asignar a cualquier otra copia ( ver teorema de estabilizador de la órbita ). Dado que el plano Fano es auto-dual, estas configuraciones vienen en pares duales y se puede mostrar que el número de colinciones que fijan una configuración es igual al número de colinciones que arreglan su configuración dual.

• Hay 7 puntos con 24 simetrías que fijan cualquier punto y, dualmente, hay 7 líneas con 24 simetrías que corrigen cualquier línea. El número de simetrías se deriva de la 2-transitividad del grupo de colinción, lo que implica que el grupo actúa transitivamente en los puntos.
• Hay 42 pares de puntos ordenados , y cada uno puede ser mapeado por una simetría en cualquier otro par ordenado. Para cualquier par ordenado hay 4 simetrías que lo arreglan. En consecuencia, hay 21 pares de puntos no ordenados , cada uno de los cuales puede ser mapeado por una simetría en cualquier otro par no ordenado. Para cualquier pareja desordenada hay 8 simetrías que lo arreglan.
• Hay 21 banderas que consisten en una línea y un punto en esa línea. Cada bandera corresponde al par desordenado de los otros dos puntos en la misma línea. Para cada bandera, 8 simetrías diferentes lo mantienen fijo.
• Hay 7 formas de seleccionar un cuadrángulo de cuatro puntos (no ordenados), tres de los cuales son colineales. Estos cuatro puntos forman el complemento de una línea, que es la línea diagonal del cuadrángulo y una colineación corrige el cuadrángulo si, y solo si, corrige la línea diagonal. Por lo tanto, hay 24 simetrías que corrigen cualquier cuadrángulo de este tipo. La configuración dual es un cuadrilátero que consta de cuatro líneas, de las cuales tres se encuentran en un punto y sus seis puntos de intersección, es el complemento de un punto en el plano de Fano.
• Existen $${\ displaystyle {\ tbinom {7} {3}} = 35}Triples de puntos, siete de los cuales son triples colineales, dejando 28 triples o triángulosno colineales . La configuración que consta de los tres puntos de un triángulo y las tres líneas que unen pares de estos puntos se representa mediante un ciclo de 6 ciclos en el gráfico de Heawood. Un automorfismo de conservación del color del gráfico de Heawood que corrige cada vértice de un ciclo de 6 debe ser el automorfismo de identidad. ^[11] Esto significa que hay 168 triángulos etiquetados fijados solo por la colinción de identidad y solo seis colinciones que estabilizan un triángulo no marcado, uno para cada permutación de los puntos. Estos 28 triángulos pueden verse como correspondientes a los 28 bitangentes de un quártico . ^[12]Hay 84 formas de especificar un triángulo junto con un punto distinguido en ese triángulo y dos simetrías que corrigen esta configuración. El dual de la configuración del triángulo es también un triángulo.
• Hay 28 formas de seleccionar un punto y una línea que no son incidentes entre sí (un anti-bandera ), y seis formas de permutar el plano Fano mientras se mantiene un anti-bandera fijo. Para cada par de líneas de puntos no incidentes ( p , l ), los tres puntos que son desiguales a p y que no pertenecen a l forman un triángulo, y para cada triángulo hay una forma única de agrupar los cuatro puntos restantes en una anti-bandera.
• Hay 28 formas de especificar un hexágono en el que no hay tres vértices consecutivos en una línea, y seis simetrías que corrigen un hexágono de este tipo.
• Hay 84 formas de especificar un pentágono en el que no hay tres vértices consecutivos en una línea, y dos simetrías que fijan cualquier pentágono.

El plano de Fano es un ejemplo de una configuración ( n ₃ ) , es decir, un conjunto de n puntos yn líneas con tres puntos en cada línea y tres líneas a través de cada punto. El plano Fano, una configuración (7 ₃ ), es único y es la configuración más pequeña. ^[13] De acuerdo con un teorema de Steinitz ^{[14], las} configuraciones de este tipo pueden realizarse en el plano euclidiano que tiene a lo sumo una línea curva (todas las demás líneas se encuentran en las líneas euclídeas). ^[15]

Teoría de los bloques de diseño [ editar ]

El plano Fano es un diseño de bloque simétrico pequeño , específicamente un diseño 2- (7,3,1). Los puntos del diseño son los puntos del plano, y los bloques del diseño son las líneas del plano. ^[16] Como tal, es un ejemplo valioso en la teoría del diseño (de bloques).

Con los puntos etiquetados como 0, 1, 2, ..., 6, las líneas (como conjuntos de puntos) son los traslados del (7, 3, 1) conjunto de diferencia planar dado por {0, 1, 3} en el grupo$${\ displaystyle \ mathbb {Z} / 7 \ mathbb {Z}.}^[16] Con las líneas etiquetadas ℓ ₀ , ..., ℓ _6, lamatriz de incidencia (tabla) viene dada por:

	0	1	2	3	4	5	6
ℓ 0	1	1	0	1	0	0	0
ℓ 1	0	1	1	0	1	0	0
ℓ 2	0	0	1	1	0	1	0
ℓ 3	0	0	0	1	1	0	1
ℓ 4	1	0	0	0	1	1	0
ℓ 5	0	1	0	0	0	1	1
ℓ 6	1	0	1	0	0	0	1

Sistema Steiner [ editar ]

Artículo principal: Sistema Steiner.

El plano Fano, como diseño de bloque, es un sistema triple de Steiner . ^[17] Como tal, se le puede dar la estructura de un quasigroup . Este quasigrupo coincide con la estructura multiplicativa definida por la unidad octonions e ₁ , e ₂ , ..., e ₇ (omitiendo 1) si se ignoran los signos de los productos octonion ( Baez 2002 ).

La teoría matroid [ editar ]

Artículo principal: Teoría de Matroid.

El plano de Fano es uno de los ejemplos importantes en la teoría de la estructura de matroides . Excluir el plano Fano como un matroid menor es necesario para caracterizar varias clases importantes de matroides, como las regulares , gráficas y cográficas.

Si divide una línea en tres líneas de 2 puntos, obtiene la "configuración no Fano", que se puede incrustar en el plano real. Es otro ejemplo importante en la teoría de matroid, ya que debe ser excluido para muchos teoremas.

PG (3,2) [ editar ]

Artículo principal: PG (3,2)

El plano de Fano se puede extender en una tercera dimensión para formar un espacio proyectivo tridimensional, indicado por PG (3,2) . Tiene 15 puntos, 35 líneas y 15 planos y es el espacio proyectivo tridimensional más pequeño . ^[18] También tiene las siguientes propiedades: ^[19]

• Cada punto está contenido en 7 líneas y 7 planos.
• Cada línea está contenida en 3 planos y contiene 3 puntos.
• Cada plano contiene 7 puntos y 7 líneas.
• Cada plano es isomorfo al plano de Fano.
• Cada par de planos distintos se intersecan en una línea
• Una línea y un plano que no contienen la línea se intersecan exactamente en un punto